试论量子通信的物理基础

2018-02-15黄志洵

中国传媒大学学报(自然科学版) 2018年5期

黄志洵

(中国传媒大学信息工程学院，北京100024)

1 引言

从正面报道看，中国的量子通信研究已取得很大成就，在世界上居领跑地位。量子通信卫星的发射和运作是标志性事件，《Science》、《Nature》杂志中有关论文也有很多是中国作者写的。不久前科技部主持了一个评比(选出“2017年中国科学十大进展”)，名列第一的是“实现星地千公里级量子纠缠和密钥分发及隐形传态”。在对成果的陈述中，提到“实现了空间大尺度上的量子力学非局域性检验”，“实现了千公里级量子密钥分发和地星量子隐形传态”，“突破了抗强度涨落诱骗态量子光源”，“突破了空间长寿命低噪声单光子检测”等[1]。……然而，对于量子通信(quantum communication，QC)国内一直有反对的声音，包括物理学家、通信专家、密码学家；他们有的反对QC的物理基础，有的不赞成量子密钥，也有人反对说“QC绝对保密、安全”。本文仅就QC的发展引发的物理学基础问题作些讨论，供有关方面参考。

对信息传送的保密是通信技术发展中的一个基本问题，其重要性不言而喻。常规通信有自己的整套方法——如何在信息发送端加入密码(编码)，如何在接收端把信号复原(解码)；以及如何让发、收两头的操作者知道同一个密钥，而且它是需要定期更换的。当前对量子通信的正面介绍和宣传，都说它有绝对保密性(或说“绝对安全”、“不可窃听”)，是否真的如此？军界、银行界等潜在用户都很关心。这个问题在国内有很大的争论，而且这种争论发展到对量子力学(quantum mechanics，QM)的认识上的分歧。这些分歧涉及微观粒子的性质，以及用QM所作描述是否完备；如何看待QM的正统诠释(Copenhagen诠释)；Heisenberg测不准关系式的正确性和意义；量子纠缠态的存在性以及由此造成的纠缠粒子相关性和非局域性；量子不可克隆原理(Wootters定理)的正确性和意义；等等。鉴于这些论题的重要性，我们作简要的讨论。

2 Bohr对量子理论创立的贡献和学术观点[2，3]

Niels Bohr(1885-1962)是量子力学(QM)的创始人之一，是后来被称为Copenhagen学派的领军人物。他于1916年任Copenhagen大学教授，1920年任该校理论物理研究所所长。1922年，Bohr因“研究原子结构及原子辐射机理的卓越贡献”而获Nobel奖。1912年他假设在原子中电子的轨道动量是量子化的，提出了原子的定态假设和频率法则，成功解释了氢原子光谱。Bohr认为，原子中的绕核作轨道运动的电子，只有在从一个轨道(2)跃迁到另一轨道(1)，才会有光辐射，其能量变化被Planck常数(h)除，就得到光辐射的频率：

(1)

上式称为Bohr频率条件；Bohr的理论对氢原子完全正确，但对多电子原子而言理论与实验不符。Bohr的早期工作不仅彰显了早期的量子论思想，也是启发后来人们的研究(这种研究导致QM出现)的重要因素。Bohr说，物理实验的根本点是用经典物理概念描述观察结果，这造成了量子理论的佯谬——我们一边建立与经典不同的定律，同时又在观察和测量时使用经典物理的概念。对此，笔者的理解是：人们在讨论微观粒子在力场中的运动时，毫不犹豫地使用诸如位置、速度、质量、动量、角动量等词汇和概念，但这些都是经典物理，在研究微观世界时能否使用并未提出证明。另外，非常明显的事实是：“粒子”、“波动”都是从经典物理学中借用的概念。

Bohr认为这是研究新物理学(量子物理)时遇到的困难之一。他说：“我们缺乏语言[2]。”另外，在经典物理范畴，做实验时可忽略测量工具(仪器)与被测客体之间的相互作用，但在量子物理中就不行。由于该二者形成为一个完整部分，这就“迫使我们放弃因果描述”，因为确定论(definity)描述的逻辑基础已不存在。他说，不得不放弃因果性这个理想观念，改用统计定律来描写自然。Bohr提醒人们注意——在量子物理的发展中不断有大量奇迹出现。

事件(客体)必须被观察到才能被知道，但观察改变了事件(客体)，这在认识论上造成了真正的麻烦。对于QM中原子客体的状况，未受观察的干扰时因果性(因果律)有效；但对处于某状态的客体做观察(测量)时，状态收缩到某一本征态。这是状态的不连续突变，QM不能描述其过程；是无确定性因果律可循的事情了。QM的几率性质凸显；Copenhagen学派认为，QM在客观实在性方面不再遵守传统的(客体在一定时空中行动的)因果性。Bohr说，正是Heisenberg奠定了一个合理的QM基础。尽管放弃了轨道图景，却保留了Hamilton正则运动方程，其对易规则为

qp-pq=jħ

(2)

ħ是归一化Planck常数；这是定量地表述对应原理。而且，必须指出QM中有一套专有的符号算子和计算规则。依靠几率函数，可把主、客观联系起来。

再看互补原理(complementarity principle)；1927年W.Heisenberg提出测不准关系式，半年后Bohr提出了互补性思想。Bohr认为，对微观粒子而言，既然同时测量位置和动量是互相排斥的，证明人们只能在互补的意义去获取对客体的认识，亦即位置和动量是一对互补的可观察量。与此类似，微观粒子在某些实验中表现为粒子，而在另一些实验中表现为“波动”，这种粒子性和波动性也是互补的——没有一个实验可同时显示这两种特性。因此，波粒二象性是互补性，是微观世界特有的现象。

1929年9月，Bohr在学术演讲中公布了他的互补原理，认为量子过程总显示出一种既互斥又互补的特性。典型例子是波粒二象性——光子理论用到了频率和波长，但这二者只有在波动图象中才有意义。粒子是空间局域的，而波则展布于广大空间。波和粒子的形象和特性仿佛互相排斥，但作为量子过程的完整描写却是二者缺一不可。又如在QM中，时空描述与因果性是矛盾的，但实际上并不能彻底抛弃其中之一。具体讲，粒子碰撞是遵循能量守恒与动量守恒的因果事件，波传播却是一种时空事件；量子过程是怎样的呢？问题在于做实验时操作者必定引入了一个因素(测量或干扰)，从而排除了二象性的某一方面，只显示另一方面(粒子或波)。这个因素是由于量子过程的基本性质(互斥又互补)而发生的。Bohr说，正是Heisenberg的测不准关系式从数量上描绘和表达了这种因素，因而可以把测不准关系式看成互补原理的一个结果(Bohr，Nature，1928，121：580)。

这个说法被Heisenberg接受了，即互补原理澄清了不确定性原理的起源。此外Heisenberg还认为，互补原理是对QM体系的Copenhagen诠释的很好总结。他们二人由分歧达到一致；互补性和不确定性成为QM形式体系的基本构成。……在我们后人(例如笔者)看来，Bohr不仅有兼容精神，而且似乎体现了一种辩证观。因此，我们不同意给Copenhagen诠释扣上“唯心主义”帽子。实际上，Bohr的位于Copenhagen的理论物理研究所，在很长时期都被看成是量子物理学的一盏明灯。

3 Born波函数几率诠释和Heisen-berg测不准关系式[2，4-8]

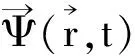
Born认识到，全新的QM不允许用确定论解释。测不准关系也强调了这一点。这并不是说在自然界的某个方面没有了因果关系，而是不能定量地计算这一关系，……笔者顺便指出，P.Dirac也有类似的论述——因果只适于不受干扰的体系(这种体系通常用微分方程表述)；然而在微观条件下，不可能在观察(测量)时不严重地干扰客体，这时不能指望发现期待中的因果联系。

Born的科学工作与Heisenberg有密切关系。Born比Heisenberg大19岁，后者曾任前者的研究助手。旧量子论中的量子条件由N.Bohr和A.Sommerfeld所奠定，对于粒子的运动可定义动量p和位置q。在普通数学中乘法服从交换率——p·q=q·p；然而现在(1925年7月)提出了突破性的对量子条件的新表述，这时的量子乘法不服从交换率——p·q≠q·p，这叫非对易性。Heisenberg提出了奇异的量子乘法规则，它来自两个量子跃迁振幅的乘积。Born意识到这可能是创造新力学(QM)的钥匙，而这不过是两个矩阵相乘的情况。Born帮助创建了QM矩阵力学的基本关系，而且绝对是量子化的；下式实际上与(2)式相同：

(3)

在这里[ ]表示矩阵，而[I]是单位矩阵；在Planck常数为零(h=0)、即非量子化条件下，p·q=q·p，回到人们熟悉的情况。Born因为这个贡献，1970年去世时上式被刻在他的墓碑上。

Werner Heisenberg(1901-1976)是德国物理学家，1923年获博士学位后即应M.Born的邀请到Gottingen大学任教，后又赴丹麦在Copenhagen大学进修。应当说，他从Bohr和Born的指导中学习了许多。1927年Heisenberg提出矩阵力学，用以解释氢原子光谱，发现奇特的双线现象并作了阐明。1927年3月他寄出的论文题为“量子理论的运动学和力学的内容”，其中包含一个最有吸引力的原理——不确定性原理(indeterminacy principle)，也叫测不准关系式，发表在Zeitschrift für Physik，Vol.43，1927，172-198，该文撼动了因果性(或因果律)，至今仍是一个有争论的问题。

Heisenberg的不确定性原理的英文也可写作uncertainty principle，我们看看他自己怎么说。1933年Heisenberg在接受Nobel奖的授奖词中说，在研究原子现象时，测量对系统干扰的无法验证的部分妨碍着经典特性的精确确定，但准许QM的应用。分析表明，确定粒子位置的精确度和同时确定其动量的精确度，二者之间存在着一个关系：

(4)

式中Δp、Δq是测量该二者时的误差，h是Planck常数。在这里，p、q是正则共轭变量。由于测不准关系式规定了这些精确度的范围，故没有完全无歧义的原子的直观图像。Heisenberg强调说，QM的规律是统计性的。测不准关系式提供了这样一个范例，即在QM中对一个变量的精确了解排斥对另一个变量的精确了解。因此，他高度评价Bohr的互补原理——同一物理过程的不同方面之间的互补关系正是QM整体上的特点。

对微观粒子而言，测量动量或坐标的任何实验，必然导致对其共轭变量信息的不确定性；故无法同时获知粒子的坐标和动量。测不准关系式表明：坐标的不确定性越小，则动量的不确定性就越大，反之亦然。因此，同时精测粒子的坐标和速度是不可能的。或者说，具有确定速度的粒子也不会有确切的空间位置。由此出发进一步可以证明，在空间任一位置找到自由粒子的几率都相同，故自由粒子的位置坐标是完全不确定的。……而且，这种测量结果的不准量之间的反比关系，对例如能量与时间之类的其他共轭变量也成立。Heisenberg说，由于自然界本身存在这样一种精确度界限，因果律不再正确。Nobel委员会在当时对Heisenberg的工作给予了高度评价；他们指出，新理论(QM)大大改变了人们对由原子、分子构成的微观世界的认识；特别是，在这里QM必须放弃对因果关系的要求，而且承认物理定律表示的是某个事件出现的几率。

4 量子力学的Copenhagen诠释品评[2-9]

物理学史书籍告诉我们，所谓量子力学的Copenhagen诠释(Copenhagen interpretation，CI)主要包含三个方面：Max Born波函数几率解释；Werner Heisenberg的测不准关系式；Niel Bohr的互补原理。对此，历史上著名的Bohr-Einstein论战，发生在1927年10月召开的第5届Solvy会议上，而在后来的第6届Solvy会议上达到高潮。……这方面的事情为什么现在又要提起？因为当代量子通信技术的发展引发了争论，以致在国内有物理学家旧事重提，认为QM的Copenhagen诠释(以下简称“诠释”)“即使在今天来看也是有问题的，Einstein并不为错”。一些学者逻辑地由此得出结论说：“量子通信是根本缺乏物理基础的东西。”既然地基都不行，盖的房子肯定有问题。这样一来，讨论和思考就把人们又带回到1927年那个时期。

有一种说法认为，Einstein不是反对QM，而是反对QM的Copenhagen诠释；我们不同意这种说法。因为这个对QM的诠释主要来自Bohr、Born和Heisenberg三人，而他们的理论正是QM的主要内容。在笔者看来，反对QM与反对QM的Copenhagen诠释在本质上是一回事；下面就来看Einstein对这三人理论的反对意见。

因果性一词的英文是causality，因果律一词的英文是causal law。相对论专家喜欢用因果律一词，暗示其为绝对不能违反的定律。然而物理学中并没有这样的定律，因果性与对称性一样只是一种信念(conviction)。它的含意为：①任何事物均有发生的原因(cause)；②任何原因都会造成某种结果(effect)；③原因必定先于结果。利用人们的日常经验的易接受性，一些人不仅把它引入自然科学研究之中，并将其置于神圣的位置和高度。

与此相联系的是确定性，英文为definity或certainty。这也是一种信念，认为大自然在本质上是可预测的，一切事件都由一个在先的原因所决定，并遵循一定规律。问题仅仅在于找到那个规律及掌握初始状态，则由现在可以精确地推出未来。1814年P.Laplace说：“世界的未来可以由其过去决定；只要掌握世界在任一给定时刻的状态(用数学表示)，就能预测未来”。这是确定论因果性的典型观点。到了20世纪，持这种观点的典型人物首推Einstein。1920年1月20日Einstein致信M.Born说：“关于因果性问题使我很伤脑筋；光的量子吸收和发射是否有朝一日可在完全因果性的意义下去理解，还是要留下统计性尾巴……要放弃完全的因果性，我将非常难受。”1924年4月29日，Einstein在致M.Born的信中写道：“在有比迄今更有力的反对严格因果性证据之前，我不会放弃……我不能容忍下述想法：受光照射的一个电子会由其自由意志来选择跳开时间和方向……不错，我要给量子以明确形式的尝试一再失败了，但我不想长久放弃希望。”1924年在致M.Born的信中Einstein又说：“量子力学理论有很大贡献，但并不使我们更接近上帝的奥秘。无论如何，我相信他不是在掷骰子”。……他的话传播很广，但并不正确；“上帝”(自然界)不仅掷骰子，而且常常掷在人们意想不到的地方。

1927年3月，W.Heisenberg提出了测不准关系式。它告诉人们，微观粒子的运行总有无法消除的不确定性，亦即在微观世界中事件的发生常常是没有原因的。实际上，正是量子理论对确定论提出了最大的挑战。从1927年10月开始，Einstein表明了对测不准关系式的否定态度，设计一些“思维实验”以证明该关系式的原理可以被超越，并与Bohr辩论。这个过程至少持续了10年，其中包括著名的EPR论文。总之，测不准关系式直接导致了不可预测性，量子世界挣脱了因果链的严密束缚。英国物理学家P.Davies说：“根据量子理论，没有因的情况下也可能有果”。中国著名量子力学家张永德说，量子理论(QT)反对Einstein的客观实在论，因为它对事物的看法是简单、机械论的，背离态叠加原理和波粒二象性。此外，为QM所不容的是Lorentz变换不变性的理论基础——相对论性局域因果性。

在QM提出前的科学发展其实已由随机性、几率性、混沌性研究预示了确定性的终结。19世纪末J.H.Poincarè发现，一些微分方程(例如Hamilton方程类型)的可解性及解值敏感地依赖于其初始条件——后者的微小变化可以导致解值巨变或无解。这一发现使“可预测性”不成为规律，在哲学上与Laplace相对立。因此Poincarè走向了非确定论，该理论认为系统的状态中任意小的不确定因素可能会逐步变大致使未来不可预测。Poincarè的一个贡献是对三体问题进行研究，从而在天体轨道的分析中发现了新的概念——混沌(chaos)。和以前的科学家一样，他解方程组、求定量解没有成功，但在定性研究方面开辟了新天地。他提出假想的n维空间——相空间概念，在相空间中每个点都代表系统的一个状态。分析结论是：渐近解有无数周期不同的序列，也有无数非周期序列——后者即混沌，它对初始条件或状态是敏感依赖的。他喜欢说的一句话是：“预测是不可能的”。

著名化学家I.Prigogine是1977年Nobel化学奖获奖者，他于1969年发表的《Exploring Complexity》认为自然界本质上是随机、不可逆、不断演化和非线性的，这才是真实的世界[10]，这与Einstein的自然观、世界观不同。……当然，根本点在于QM揭示了量子世界中微观粒子的运行，与确定论因果性相悖。在QM中微观粒子行为通常不可预测；如把粒子到达某处当作一个事件，它就可说是无原因的。无论Einstein或者后人都把因果性绝对化了。实际上，在QM提出之前人们也已认识到正确完整的因果描述常常做不到，必须接受事件的发生可以无确定原因。

虽然大多数物理学家都肯定M.Born和W.Heisenberg的成就，但在Einstein那里，这二人的工作都招致反感——他认为Born和Heisenberg的工作都“脱离了正常的道路”。他相信客观世界是确定性的；例如通过云室能清晰地看见径迹，就不应该不考虑其轨道。总之，Einstein在1927年10月的第5届Solvy会议上明确说：“不接受确定性原理”。他还反对把量子力学看作单个过程的完备理论，因为它可能出现超距作用。Einstein说，他不把de Broglie-Schrödinger波看成单个粒子，而是当作分布在空间的粒子系综。实际上，Einstein是把波动看成大量粒子的平均行为。1934年3月22日，Einstein在致函Born时再次表示反对几率诠释。

1948年Einstein在《辩证法》杂志上发表的文章“量子力学与实在”，可以看作是他在晚年的表态。虽然他承认量子力学是“标志物理知识的重大进步，甚至是决定性的进步”，但又坚持说“量子力学方法根本不能令人满意”。这种态度矛盾的声明一方面是由于QM的深刻性和应用的广泛性已使他无法再否定其意义，但又不甘心承认自己在学术见解上错了。因此，笔者不认为Einstein在晚年改变了反对QM的态度。但有人至今还说相对论(SR、GR)可以与QM相结合，这岂不荒谬可笑？……在Einstein发表上述文章的20多年后，两位大师级的物理学家的评论发人深省——已到晚年的P.Driac说“要使相对论和量子力学一致起来是存在真正的困难”；S.Weinberg则说“理论物理学有大问题，例如对Lorentz不变性的要求根本不是QM能够满足的”。应当说，这二人的表述非常清楚正确。

QM出现的1926年～1927年，距狭义相对论(SR)的提出间隔了21～22年，距广义相对论(GR)的提出间隔是11～12年。可以说，相对论一方面成就了Einstein的巨大威望，同时又使他趋于保守；这是令人遗憾的。

5 讨论

科学界中的“学派”，是指在一个理论框架下逐步聚集了一群人，他们在基本观点上一致，但又有各自的贡献。不同学派间会有竞争和对立，但其交流、辩论是健康的。量子力学的Copenhagen学派的形成有一个过程；1912年春N.Bohr到英国物理学家D.Rutherford处工作，同年回到Copenhagen后不断思考氢原子线光谱的实验规律；1913年Bohr提出原子中电子绕核公转的量子化轨道运动理论，又提出两个新概念——光辐射或吸收是原子中发生量子跃迁的结果及电子公转时的角动量量子化，证明Bohr是一位十分出色的创新型科学家。1916年Bohr任Copenhagen大学理论物理教授；1920年他创建理论物理研究所，欧洲多国学者来所工作。1922年W.Paul、1924年W.Heisenberg进入该所是标志性事件，他们都是著名的A.Sommerfeld的学生。此外，来到Bohr这里做研究的还有P.Driac、P.Ehrenfest、L.Brillouin、L.Landau、G.Gamov等人，如所周知他们都在后来做出过重大贡献。当然，根本点在于Bohr领导下的人们(特别是Heisenberg和M.Born等)提出了新的理论系统——量子力学(QM)，其独特的数学表达方式和物理思维方式与经典物理截然不同，其正确性逐步被证明；这才使Copenhagen学派名声大噪，有许多仰慕者和追随者。

Copenhagen学派的领军人物是N.Bohr，反对派的领军人物是A.Einstein。当QM问世时，Einstein已47岁，是一位饮誉世界的科学家——因为他的相对论(1905年的SR和1915年的GR)，也因为他用光子学说解释了光电效应而获Nobel物理奖。Einstein在推导光子的理论表述时是用经典物理(在1905年根本没有QM)，他却能参考Planck量子论完成了对光子的推导，是革命性的工作。但在QM出现后他却坚持反对；直到1955年去世，态度未变。

为把讨论引向深入，我们列表说明以Bohr为代表的Copenhagen学派的观点与以Einstein为代表的反对派观点的主要分歧所在，见表1。……现在有人说“Einstein不是反对QM，而是反对Copenhagen解释”，这句话值得推敲。为明确起见，笔者提出一个表达式：

QM≌CI+SE+DE

(5)

上式左端的QM代表构成量子力学的全部内容；右端：CI代表Copenhagen诠释的主要内容(Bohr、Heisenberg、Born)，SE代表Schrödinger量子波方程，DE代表Driac量子波方程。SE、DE都是QM的重要组成部分，但却不是“诠释”的内容。按照这个表达式(虽然是不精确的描述)，反对CI不等同于反对QM。尽管如此，笔者仍然认为Einstein所反对的正是QM的某些核心思想，那么怎能说他“不反对QM”？

另外，表1呈现了有趣的情况——1926年上半年E.Schrödinger从经典力学出发导出了SE，而他却不支持“诠释”，站到了Einstein一边。1928年Driac从相对论力学出发(至少从表面上看是从SR出发)导出了新的量子波方程(DE)，他却成为Copenhagen学派的一员。众所周知，1926年上半年E.Schrödinger创造了QM的波动力学，即QWM[11-14]；其核心是描述微观粒子体系运动变化规律的QM基本运动方程——Schrödinger方程(SE)。M.Planck认为该方程奠定了量子力学的基础，如同Newton、Lagrange和Hamilton创立的方程在经典力学(CM)中的作用一样。Einstein的说法稍有不同，他相信Schrödinger关于量子条件的公式表述“取得了决定性进展”，但Heisenberg和Born的路子则“出了毛病”。Einstein为什么比较喜欢Schrödinger的工作而总对Heisenberg的工作抱有反感？可能是因为他认为前者的理论并非完全抛弃确定性的，与后者对确定性的决绝态度不同。当然由此也可知道，Newton的经典力学和Einstein的相对论力学，都是确定性的理论。

表1 量子力学大辩论

Schrödinger量子波方程的推导是从Newton经典力学出发的，称为非相对论性量子波方程。这个方程独特和出色之处在于：它把核外电子轨道或分立能级当作波方程的本征值；但SE有经典物理的痕迹，当我们写出

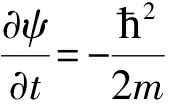
(6)

会立即注意到这里有粒子质量m，这绝对是经典物理的参数和概念。而且，这个方程给人以下述印象：经典物理中任何过程都在一定时空中发生并连续地发展的概念，是被保留下来了。尽管推导SE时没有从SR出发，但这个方程(至少从表面来看)，并不反对相对论性的自然观。

SE是QM的核心理论之一，重要性相当于经典物理中的Newton运动方程。它对自然现象有预言能力，应用广泛。但Schrödinger把全部热情放在波动上；按照de Broglie和Schrödinger的思想，运动粒子速度与波包的群速相同，故他们的理论暗示波包和粒子是一回事。这样看待微观粒子与相应波动的关系夸大了波的地位，是错误的。我们从非相对论性自由粒子出发作简单推导；可以证明，de Broglie波的色散方程(ω～k方程)为

(7)

式中ħ=h/2π，k=2π/λ；故可求群速

(8)

故群速与粒子速度相等。由上式出发计算群速vg，对波数k的导数：

(9)

故vg与k有关，说明波包在传输过程中会扩散(发胖)。但粒子在传输过程中却是稳定的，故科学界拒绝了他们的观念；还开玩笑说：“Schrödinger方程比Schrödinger更聪明”。

正是Bohr指出波传输过程中波包会“发胖”，而粒子却有无可置疑的稳定性，故简单地把粒子看成波包说不通。尽管如此，Schrödinger却不接受CI的“波粒二象性”和“波函数坍缩”。据说，是Einstein鼓励他设计一个思维实验来反驳CI。在1935年的文章中(Naturwissenchaften，1935，Vol.23，807、823、844)，Schrödinger提出了所谓“Schrödinger猫态”的悖论——假设有这样一种装置，用原子的衰变来触发小锤，将装有毒气的小瓶砸破，小瓶释放毒气把猫毒死。其中原子的衰变是随机的量子事件。问题是，原子的衰变是多种状态的叠加，称为叠加态，这意味着猫同时处于死与活的状态。一旦进行测量，量子叠加态就会被破坏。也就是说，一旦我们打开盒子查看结果，猫就只会处于一种状态，即要么活着，要么死了。但这并不意味着打开盒子之前猫就已经处于这种状态——在观测前，猫处于“生死叠加”状态，是荒唐的。一个同时处于两种状态的量子系统决定了猫的生死。这个实验表明，量子理论和人们的直觉相违背。Schrödinger猫佯谬对Copenhagen学派是一个打击，因为猫不可能是“既死又活”的[15]。

但是Schrödinger设想的思维实验有一个前提：波函数可描写宏观物体(包括生物体)，而这一点却缺乏证明。然而这个“猫佯谬”的讨论并非没有价值，它与同年(1935年)发表的EPR论文有内在的联系。EPR讨论的复合体系(二粒子体系)的不可分离状态其实就是纠缠态(entangled state)，而这个词语正好出现在Schrödinger论文中，故纠缠态问题也称为Schrödinger猫佯谬。Schrödinger使用纠缠态一词是为了描写复合体系的不能表示为直积形式的叠加态，并用思维实验说明：波函数几率诠释如用于宏观世界会得出荒谬的结论。

虽然Bohr的互补原理应用广泛而不限于光的波粒二象性[2，8]，但人们习惯于从这个二象性问题来看待互补原理。“诠释”认为，无论有质量粒子或无质量粒子都有波粒二象性；它们有时呈现为粒子(有确定路径，但不产生干涉条纹)，有时呈现为波(无确定路径，但产生干涉条纹)。这取决于实验者如何观测，但不可能同时观察到两种属性，即不会掌握粒子路径的同时又出现干涉条纹。N.Bohr的互补原理大致上也是此意。然而在2014年情况有了变化——波粒二象性研究的最新进展已证明[16]，在同一干涉仪装置内安装两套好的测量装置(路径信息和干涉条纹探测器)，分别完成不同功能，互不干扰，以正确方式协同作用，则可能同时观测粒子性和波动性。这就表示“绝不会同时观测到两种属性”的传统观念可能会被打破。中国科学院物理所李志远研究员一直做“微观粒子波粒二象性及互补原理违背可能性”的研究。……不过，笔者认为即使互补原理不完备也无损于把QM作为QC的物理基础。

6 量子纠缠态存在性问题[17]

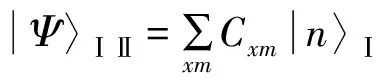
(10)

这里Ⅰ和Ⅱ有纠缠的量子态，表示对Ⅰ的测量与对Ⅱ的测量相关，不管Ⅰ、Ⅱ之间距离多远。这是由于复合体系量子态的叠加所造成的。这种量子纠缠态是量子信息学的物理基础之一。

纠缠态的事情起源于1935年的EPR论文[18]。这篇文章的局域性原则与狭义相对论一致，坚持能量与信息以超光速传送的不可能性，坚持在类空的分离体系(Ⅰ和Ⅱ)之间存在超距作用的不可能性。用思维实验说明QM是违反局域性原则的，而这正是在QM中分离体系有超距作用的根本原因。

1927年Heisenberg不确定性原理的出现使Einstein震惊，但他认为EPR论文可以驳倒该原理并证明QM不完善。EPR中的两个体系(Ⅰ和Ⅱ)的讨论中似乎表示“既测知位置又知道速度”是可以办到的，因为Ⅰ的速度即Ⅱ的速度。文章发表后，Bohr起而反驳[19]。Bohr的意思是EPR论文中的设定可以被驳回——不确定性既影响Ⅰ又影响Ⅱ，在测量Ⅰ时Ⅱ立即受影响从而使结果与Newton定律一致。这种作用会即时发生，即使Ⅰ、Ⅱ相距很遥远。……

俄罗斯的V.Fock院士说[20]：“在量子理论发展初期曾为它作了许多工作的Einstein，对近代的量子力学却采取了否定态度，这是特别令人惊异的。……EPR思维中的两个子系统之间没有直接的力的相互作用，一个也能影响另一个，Einstein认为不可理解，从而认为量子力学不完备。”Fock认为，量子力学中Pauli原理的相互作用(影响)是一个非力的例子。具有共同波函数的两个粒子可能发生相互作用，即纠缠。当然，Fock院士所说的相互作用(影响)，现在通常称之为“量子相关。”

根本之点还是J.Bell在1965年提出了著名的不等式(Bell不等式)作为判据[21]。Bell的分析建筑在Bohm的自旋相关方案(自旋双值粒子体系)及隐变量(用λ表示)理论的基础上。Bell论文的出发点(假定)共三个，即自旋双态系统(spin two state system)、理想相关(perfect correlation)和局域性条件(locality condition)。由于Bell不等式提供了实验研究的可能，从1973年起掀起了实验热潮——不仅为了检查QM的正确性，也逐步揭示了量子纠缠(quantum entanglement)现象的存在。1982年，法国物理学家A.Aspect[22，23]的实验最为精确，其结果与QM相符，而且是与QM预言非常好的相符。这绝非偶然，而对QM专家来讲也并不意外。值得注意的是，Aspect实验是动态的而非静态的，即实验装置在粒子飞行过程中随时间改变；这是J.Bell的希望，因为这样一来局域性条件就变成Einstein因果性(任何信号都不能超光速)的直接结果了。实测的结果，Bell参数S=0.101±0.020，与QM计算结果(S=0.112)十分接近，而与Bell不等式的规定数据(-1≤S≤0)相差很远。

在Aspect实验以后，不断有新的实验出来，证明QM正确而量子非局域性(quantum non-locality)存在。双粒子源的产生在技术上得到解决，其飞出去以后仍能保持相关(即纠缠)的距离也在增加。例如，1998年G.Weihs等在空间距离400m的条件下(Aspect实验仅为15m)，用波长702nm的双光子进行实验，结果也是违反不等式而完全支持QM。……这类“Bell型实验”提供的双粒子(双光子)纠缠距离一再突破，于2007年达到144km之远，令人吃惊。对这些实验，法国物理学家B.d’Espagnat评论说：“局域性实在论几乎肯定有错误”；“只能通过放弃Einstein可分性假设来解释对Bell不等式的违反”。他还认为，虽然J.Bell在推导不等式时有3个前提，但局域实在性假设是最基本的。……笔者认为，其实N.Bohr早就阐明了“不可分性”原则，即在量子领域中可分性失效——系统的两个子系统即使分开也不是完全独立的存在，测量一个必定影响另一个。

在欧洲核子研究中心工作的John Bell，1985年在接受媒体采访时，先说明Bell不等式是分析EPR推论的产物，该推论说在EPR文章条件下不应存在超距作用；但那些条件导致QM预示的非常奇特的相关性。由于QM是一个极有成就的科学分支(很难相信它可能是错的)，故Aspect实验的结果是在预料之中的。“QM从未错过，现在知道了即使在非常苛刻的条件下它也不会错”，“肯定地讲，该实验证明了Einstein的世界观站不住脚”。……这时提问者说，Bell不等式以客观实在性和局域性(不可分性)为前提，后者表示没有超光速传递的信号。在Aspect实验成功后，必须抛弃二者之一，该怎么办呢？这时Bell说，这是一种进退两难的处境，最简单的办法是回到Einstein之前，即Lorentz和Poincarè，他们认为存在的以太是一种特惠的参照系(prefered frame)。可以想象这种参照系存在，在其中事物比光快。有许多问题，通过设想存在以太可容易地解决。Einstein除掉以太只是使理论更简练。在发表了这些惊世骇俗的观点后，Bell重复说：“我想回到以太概念，因为EPR中有这种启示，即景象背后有某种东西比光快”。但这种以太在观察水平上显示不出来。……“实际上，给量子理论造成重重困难的正是Einstein的相对论”。

然后是英国著名物理学家David Bohm，他曾在1951年以现代形式对EPR思维作了表述。在提问时，主持人把“局域性”(locality)直接定义为“宇宙的不同区域不能互相传送超光速信号的观念”。而Bohm则说，(由于Aspect实验)他完全准备好了“放弃局域性”，但并未放弃相对论，而是把它看成更广泛的某种学说的近似。Bohm明确表示，他“接受超光速信号的概念”；只要做现有类型的实验，相对论就仍有效，但在更深层次可能发现有某种超光速的东西。对于Einstein，Bohm认为有些事情是按他预料那样发生的，但是“Einstein不可能在每件事上都正确”。另外，Bohm主张用“相关”一词描写那种联系，用“信号”一词就不合适，因为这个词包含了信息传递的含意。

以上两人之中，Bohm采取如下态度：批评Einstein的物理观、哲学观，但不放弃相对论。Bell却明显表示了与Einstein的相对论决裂的意思。可惜J.Bell去世太早(1990年)，来不及看到在他去世后的20多年中各国开展的超光速研究[25]。……在今天，实验家A.Aspect仍然健在并发出自己的声音；2012年他曾讲述38年前(1974年)第一次看到Bell论文时的激动心情[26]。Bell论文与1935年的EPR论文直接相关，但它先是发表在一份不出名的刊物上，几乎不为人所知。在那个没有互联网的时代，优秀论文的传播是靠复印机，Aspect拿到的正是Bell论文的复印件。他说：

“我沉浸在Bell带给我的震撼中，我决定将自己的博士论文聚焦于对Bell不等式的实验检验。……通过实验可以精确检查两种相互冲突的理论(量子力学和Einstein的局域性实在论)到底谁对。Einstein的local realism包含两个原则——系统存在物理实在，而局域性假设来自相对论。最终我的实验证明量子力学正确，并迫使大多数物理学家放弃了Einstein竭力维护的局域性实在论”。

Aspect说，非局域性明显违背相对论，很奇特。一系列基于光子对(pair of photons)的实验尽管看起来不可思议，但却验证了量子理论的有效性。N.Gisin已利用日内瓦的电信光纤网展示了相距数十公里的量子纠缠性质存在，让人们颇感意外。Aspect认为，Gisin的一些实验已证实了遥远物体间能发生纠缠(笔者注：“物体”应理解为微观客体)，而且也是把量子纠缠应用于量子密码学的首批科学家之一。……总之，Aspect直到现在仍希望非局域性物理实在能与相对论“共存”。是否真能做到，那就另当别论了[27]。

在西方科学界，Einstein的相对论被置于神圣的地位。虽然也有一些著名物理学家(如H.Dingle，L.Essen，M.Pavlovic，T.Flandern，J.Maguejo等人)对这个理论体系本身或其结果提出批评，甚至物理学大师Paul Dirac也在晚年与Einstein的理论拉开了距离[27]。但在主流的科学共同体中，相对论仍然如同《圣经》，绝对不能违反。因此，虽然Aspect也说自己“不认为有什么不可触碰、无法更改的物理理论，它们都可能被适应性更广的理论所取代”；但是，在是否可能存在超光速的问题上，老年的Aspect与中年时的他在认识上没有区别。或许他不清楚在世界各国已蓬勃开展超光速研究的现实；但不管怎么说，直到2012年Aspect实际上仍然不能面对“Einstein的理论和观念存在问题”的事实。

量子纠缠是真实存在的物理现象。尽管其本质尚未完全弄清楚[28，29]，但展开应用性实验研究是必要的和正确的。瑞士日内瓦大学N.Gisin教授的团队，多年前就测出纠缠态传播速度为(104～107)c[30]，即不是无限大而有确定速度(超光速)；这与引力传播速度、静电力场传播速度很像，是有限但很大的(超光速的)速度[25]。实验摆在那里，怎么能说纠缠态不存在？当然，有的物理学家坚守Einstein的局域性实在论物理观，那是他们的自由，但他们也应看到在全世界展开了蓬勃的量子信息学(QIT)研究，应当多了解实验物理学家做了些什么。

7 关于Wootters定理

量子信息学时代似乎突然来到人们身边，我们真的能象使用智能手机那样应用量子通信方式吗？许多人在问这个问题。既然“物理学家不懂通信、通信专家不懂量子物理”的情况大量存在，从事量子通信实验研究的人们就应当对自己的工作成果和国际上的动向作实事求是的说明，绝不能利用公众的无知作夸大宣传乃至误导。特别是不能宣传一种“量子神学”，使自己和别人都落入唯心主义的泥潭。例如，什么是“量子隐形传态”(原文为quantum teleportation)？在说明和宣传时应当慎之又慎。简言之，量子通信(QC)必须以实践的结果来说明自身的存在性和意义，立论的根本点当然还是其安全、保密的实际效果，并拿出最关心通信保密的业界(如军方、银行业)已接受QC并取得良好效果的例子来，才能证明自己。很遗憾，目前似乎尚无这方面的消息。

量子通信为何保密性好？最通俗的解释是这样的——Heisenberg不确定性原理(测不准关系式)造成下述情况，即当窃听者不知道发送方编码基时，无法准确测量获得量子态的信息；另外，量子态不可克隆原理(Wootters定理)使窃听者不能复制一份量子态以在得知编码基后作测量，故窃听造成误码。这时通信双方知道被窃听了，随即停止通信。

在以上陈述中未提纠缠；实际的量子通信系统多种多样，似乎直到2004年才用上纠缠光子于QC技术之中。故纠缠似非保密通信的必要条件。……总之，量子通信的研究者认为，是Heisenberg测不准原理和Wootters量子不可克隆定理保证了BB84协议的“无条件安全性”。假定保密者从量子信道截获光子并作测量，而这种窃听行为会干扰量子态，从而使发、收端的操作者知觉有人窃听，便停止通信。但保密者也可不作测量，而是复制出同样的(带有密码信息的)东西。然而1982年W.Wootters[31]提出了“量子态不可克隆定理”，从而否定了该作法的可能性；这就维护了量子加密的权威性，被认为是不可破解的。这里引用中国科学院的一份文件的话——“量子密钥分发采用处于叠加态的单光子来确保相互远离的双方间的无条件安全性”[32]。

2013年西安电子科技大学裴昌幸等[33]出版了一本研究生教材《量子通信》，该书对Wootters定理的陈述为：“在量子力学中，不存在实现对一个未知量子态的精确复制这样一个物理过程，使得每个复制态与初始量子态完全相同”。并且说，利用状态空间的线性性质，可以简单证明在量子信息中非常著名的单量子态不可克隆定理。书中提出了两种证明方法：

①设有输入量子态|ψ〉和|φ〉，初始状态为标准纯态|s〉。

由U(|ψ〉|s〉)=|ψ〉|ψ〉，U(|φ〉|s〉)=|φ〉|φ〉，得

U[α(|ψ〉+β|φ〉)|s〉]=(α|ψ〉+β|φ〉)(α|ψ〉+β|φ〉)

=α2|ψ〉|ψ〉+βα|φ〉|ψ〉+

αβ|ψ〉|φ〉+β2|φ〉|φ〉

(11)

另外，又有

U[α(|ψ〉+β|φ〉)|s〉]=αU(|ψ〉|s〉)+βU(|φ〉|s〉)

=α|ψ〉|ψ〉+β|φ〉|φ〉

(12)

二者矛盾。所以量子态不可克隆。

②有两个量子系统：A为待克隆的量子态，初始态为|ψ〉；B表示初始时处于标准纯态|s〉。克隆由A、B复合系统上一个幺正算子U描述，即U(|ψ〉⊗|s〉)=U(|ψ〉⊗|ψ〉)对∀|ψ〉成立。则对|φ〉≠|ψ〉也有

U(|φ〉⊗|s〉)=U(|φ〉⊗|φ〉)

取内积，且U+U=I，对于纯态|s〉，有[〈s|s〉]=I，则

(|φ〉⊗〈s|)U+U(|ψ〉⊗|s〉)=(|φ〉⊗|φ〉)(|ψ〉⊗|ψ〉)

<=>〈φ|ψ〉〈s|s〉=〈φ|ψ〉〈φ|ψ〉

(13)

可见，〈φ|ψ〉=0 或者〈φ|ψ〉=I，即两个态相正交或相等。

以上推导表明：成功率为1的量子克隆机只能克隆一对相互正交的量子态。即如果克隆过程可表示成一幺正演化，则幺正性要求两个态可以被相同的物理过程克隆，当且仅当它们相互正交，亦即非正交态不可克隆。

然而2018年梅晓春、李小坚[34]给出了“量子态不可克隆定理不成立”的证明。文章说，在证明“量子态不可克隆定理”的原始论文中，Wootters首先假设任意一个量子态都是可以克隆的。然后定义了一个量子态克隆算符，推导出了另外一个量子态可以克隆的两个条件。一个是正交条件，另一个是非正交条件，即这两个量子态的乘积的积分等于零或等于1。满足这两个条件的量子态都是可以克隆的，不满足才不可克隆。因此根本就不存在量子态不可克隆的问题，而是什么样的量子态可以克隆的问题。研究还发现，对于一般的量子体系，可以有无穷多的量子态满足这两个条件，所谓的量子态不可克隆的说法是错误的。

此外，Wootters定义的量子态克隆算符有严重问题。将这个算符作用于一个被克隆的波函数，结果不变。将它作用于标准的纯态波函数，却可以将它变成被克隆的波函数。这样的结果显然自相矛盾，因为纯态波函数也是波函数，因此量子克隆算符在数学上不成立。

梅、李文章共有23个编号公式；如梅、李文章的推导分析正确，“用量子通信可以无条件地获得绝对保密”的说法即不成立。不过，有人认为梅、李文章中说“激光器可以大量克隆光子”是不对的，因为激光器虽利用受激辐射工作，但不可避免会自发发射，故不能说一定能克隆。他们认为量子态不可克隆是早有定论的。……对此事笔者另有看法——即使Wootters定理无懈可击，QC也不可能“绝对保密”；否则，也不用(自2004年)采用诱骗态来构建QC系统了。

8 结束语

量子力学(QM)从提出至今，已有92年的历史。现在，它已成为现代物理学的基础与核心，其巨大影响还在不断地扩展。一系列的相关实验，诸如关于Bell不等式的判别实验，关于波粒二象性的新实验，关于量子隧穿呈现出来的超光速性实验，以及近年来关于量子纠缠态传播速度的实验，关于量子通信的各种实验，等等；均已超越了哲学思辨式的探讨，显示出一系列全新的非经典物理现象，引起了人们的极大关注。近年来，不仅有众多科学工作者在从事QM基础理论与量子信息学(Quantum Information Technology，QIT)理论与实验的研究，论述QM的新著作也还在不断出版；这是非常可喜的。

与此同时，也引发出一些争论，甚至是激烈的争论；这本属正常。但是，有的文章却在缺乏事实依据的情况下企图否定QM这一理论体系，至今不承认QM这一伟大理论，在物理概念上也造成了一些混乱。1965年，R.Feynman曾说过一句名言：“I can safely say that nobody understand Quantum Mechanics”，这话或许说明学习和理解QM的困难。但如不抱门户之见(甚至是太深的门户之见)，对QM的基本理论还是能有确实的把握和正确的理解的。量子信息学的进展和成就，也是有目共睹、不容否认的；这是绝大多数物理学家的看法。QM是一个成功的理论，Einstein的态度不太妥当，这些都是明显的事实。即使它不十分完备，也足够做QIT(包括量子通信QC)的物理基础。至于宣传说QC绝对安全保密，我们不能同意！

笔者强调指出QM发展到今天，其理论博大精深，其应用既广泛又卓有成效；只有承认这两点，才能开展冷静客观的讨论。至于对Copenhagen诠释的看法，1992年C.Cassidy[7]说，QM的Copenhagen诠释“从根本上改变了我们对自然的理解，标志着物理学的一次深刻变化。而且，后来也没有出现别的理论能像该诠释那样对微观现象如此深刻的认识和广泛的应用。”笔者同意这样的说法。这样讲并不意味着“诠释”没有任何问题，也不代表不允许人们对它作批评。正如中国物理学家卢鹤绂[35]所说：“量子力学数学形式自1925年至1927年建立以来，尽管不时有所精炼和推广，它经受得起理论上和实验上的考验，在30年代就已定型，直至今日仍牢牢确立而无变动。但其物理解释，在数学定律背后的物理实在究若何，则长久以来一直争论不休，仍无定论。”大师级人物de Broglie也说过这样的话[20]：“今天的物理学家几乎一致同意Bohr、Heisenberg的解释，因为该解释似乎是唯一能符合全部已知事实的。”这些冷静客观的评论，应当能使现在的人们清醒。

不过，也要看到有人为了否定量子通信，仍在基础理论层面做文章。有的说法似是而非；例如关于QM非局域性的来源，有的文章一方面说这来源是“QM方程没有彻底满足相对论所致”，但接着又说连Klein-Gordon方程和Dirac方程也是非局域的，而这两个方程是公认的相对论性方程。这样讲是自相矛盾的，而且与Einstein责难“QM是非局域的”原意不符。Einstein从未谈及非局域性是指方程的，从第5次Solvay会议(1927)上的发言到EPR论文(1935)，都是阐述QM描述方式所导致的非局域性。看来，有的作者本想追随Einstein，却未弄懂后者的原意。

QM的方程是局域性的，描述方式是非局域的，这是QM基本原理的必然结果。构成QM框架的原理有好几条，不是一个方程所能代替的。例如，纠缠态的存在即由于下述原理：①波函数Ψ完全描述粒子状态及其统计解释；②Ψ满足态叠加原理(这是波动性的体现和要求)及测量假设；③全同性原理(全同粒子不可区分性，要求其体系波函数必须对称或反对称)。上述要求缺一不可，但与它满足哪个QM方程无关。

至于有的文章所说的“非局域性另一来源是出自Fourier展开”，也是不正确的。QM只是拿Fourier展开一用而已。显然，它把该数学定理误认为是QM的态叠加原理或测量假设了。数学定理的展开各项不一定代表量子态，而物理原理的各项必须是量子态。将二者混为一淡是错误的。