移动区域中的电场问题的研究
2018-02-15刘小妹闫述涛
刘小妹,闫述涛
(中国传媒大学理工学部,北京 100024)
1 引言
电磁推进系统是以导轨和电枢为主要组成部分,通过对导轨两端施加电压,使导轨内产生电流,在电流和导轨间磁场的共同作用下,进而产生作用在电枢上的洛伦兹力,通过洛伦兹力对电枢的作用来加速抛体运动的装置。移动过程中,导轨与电枢接触面随时间变化,导致电场、电流也随之变化。求解问题模型如图1,其中最外层是空气层,中间为两条导轨,导轨中间是滑动的电枢,在导轨两端通电,由导轨与电枢构成一个闭合回路。
2 理论模型
在求解区域中,我们将在两个导轨上分别添加适当电压,我们通常给予150V和-150V的电压,利用磁矢量A和标量电位u表示的麦克斯韦方程来求解电场与磁场的分布。已知麦克斯韦方程的微分形式为
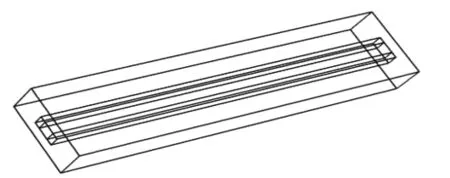
图1 电磁轨道推进系统模型

(1)
又有
D=εE,B=μH,J=σE
其中,H:磁场强度;J:电流密度;D:电位移;E:电场强度;B:磁感应强度;ρ:自由电荷体密度;μ:磁导率;σ:电导率;ε:介电常数,这里我们忽略电位移的影响,将问题简化为涡流方程,那么(1)式变为:

(2)
因此,涡流场方程可以从(2)式中导出,选择磁矢量A和标量电位u组成的电磁位对,将含有运动电枢的麦克斯韦方程组变换为:
▽·(-(σ▽u))=0
(3)

(4)
(3)式和(4)式可以视作涡流场控制方程的统一形式。在图1中,在导轨和电枢及导轨间的空气中需要描述电场和磁场,因此(3)式和(4)都需要用到,而在最外空气层中,只需描述磁场即可,因此我们只需要用到(3)式。
在忽略了电位移的影响下,问题中还涉及到边界的问题,我们需要处理好在边界上电场与磁场的条件,我们设在边界上:
n×A=0
(5)
n·J=0
(6)
式中n为交界面的法向量。另外,为了保证磁矢量解的玩唯一性,我们还要满足库仑规范条件:
▽·A=0
(7)
满足(3)、(4)式之后,我们还需考虑一个问题,电枢的运动是一个瞬时问题,电枢随着时间变化而移动,我们需要确定电枢运动的轨迹。前面有文章采用的是主丛匹配法,这里,我们利用电导率的不同来确定电枢在导轨间的位置。在两个导轨之间,存在着电枢和空气,电枢和空气的电导率是不同的,在模型中,电枢我们采用的是铝,铝的电导率为3.77×107(S/m),而空气的电导率为1.0(S/m),我们通过在导轨间不同时间、不同位置电导率的不同,就可以很容易的判断出不同时间下电枢的位置,我们取如下函数表达式作为两导轨之间相同时间下不同位置电导率:
σ=σ_air+σ_al*e-100*(|x-x0|>(L/2))*(|x-x0|-(L/2))
(8)
其中σ_air是空气的电导率,σ_al是铝的电导率,L是电枢的宽度,x是导轨间位置坐标,x0是电枢的中心点坐标。随着时间的变化,坐标产生变化,从而两道轨之间不同位置电导率发生了变化,因此就可以确定电枢移动的位置。
3 有限元分析
为了便于计算我们只考虑在导轨、电枢以及导轨之间的空气中的电场问题,并且只需要考虑(3)式,因此为了便用于仿真模拟软件的执行,需要通过变分形式,取试探函数v(x),我们将(3)式改写成弱形式:
(-σ▽u,▽v)=0
(9)
并且在两条导轨上,设置边界条件为一条导轨上通入150V电压,另一条导轨通入-150V的电压。这样,我们就可以对该模型进行仿真模拟分析。
4 数值实验
利用仿真模拟软件对电磁轨道推进系统进行模拟,首先是对电场的动态变化的分析,为了简便运算的复杂程度,我们取导轨的长度为1,电枢的宽度L为0.04,电枢的中心x0=0.02,选择让电枢每个时间单位移动半个电枢的长度,图2、图3为动态模拟结果。
通过模拟结果,我们可以看出,随着时间的推移,电压随着电枢变化而变化,导轨所在的位置即电压达到的位置,并且在电枢初始未与导轨接触时和电枢弹出时,整个导轨电压达到顶端。同样,电流也是随着电枢的移动而变化,在导轨上电流总是从高电压流向低电压,并且电枢处的电流相对于导轨上的电流较小,也同样,在电枢初始状态未与导轨接触时和电枢弹出时,电流也随之消失。

t=10s t=20s

t=30s t=40s图2 电场随时间变化图
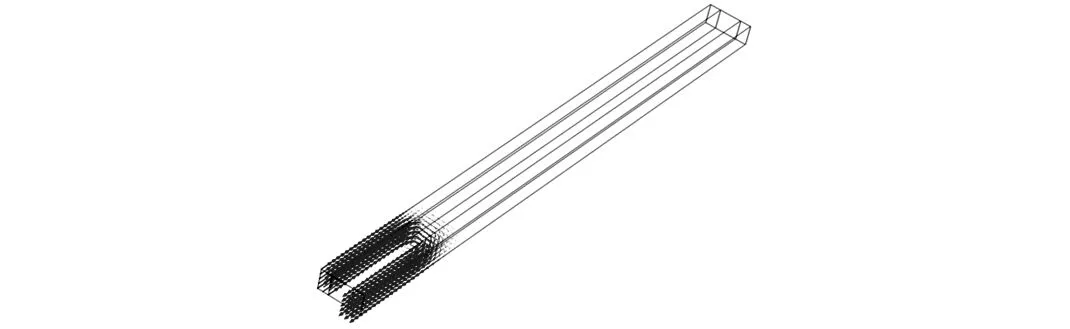
图3 20s时电磁轨道电流分布
5 结论
本文是在将电磁推进系统简化的情况下对其电场、电流进行理论分析、数值模拟。我们假设电枢在导轨间进行匀速运动,这样不仅可以简化计算,而且可以更加直观的通过仿真模拟软件观察电枢的运动状态,更好的分析电磁推进系统的电流及电场的变化情况。
