二次时变参数离散灰色预测模型的进一步推广

金梦迪，刘基伟，张辉

(中国传媒大学 理学院，北京 100024)

1 引言

由于对可靠小样本统计的需求日益增长，小样本预测是一个很重要的课题。多年来，学者们对小样本非平稳时间序列的预测问题做了深入研究，突出问题是，对于非平稳时间序列，当系统受到干扰的严重影响时，过去的可用数据不能如实反映系统的规律。因此，为使预测模型的扰动界变小，引入分数阶经典弱化缓冲算子，对原始序列进行微调来提高预测精度；并且通过建立二次时变参数离散灰色模型对实例进行研究验证。

2 分数阶弱化缓冲算子的构造

经典弱化缓冲算子充分考虑每个数据的优先性，而变权弱化缓冲算子只考虑最新一个数据的优先性，所以从综合利用原有数据信息的角度考虑，经典弱化缓冲算子是一种不错的缓冲算子。

容易证明，经典弱化缓冲算子的阶数越高，越能体现新信息的作用，提高预测质量[2]。但是经典弱化缓冲算子不能实现缓冲作用强度的微调，本文引入分数阶弱化缓冲算子。

一阶弱化缓冲算子的矩阵形式为：

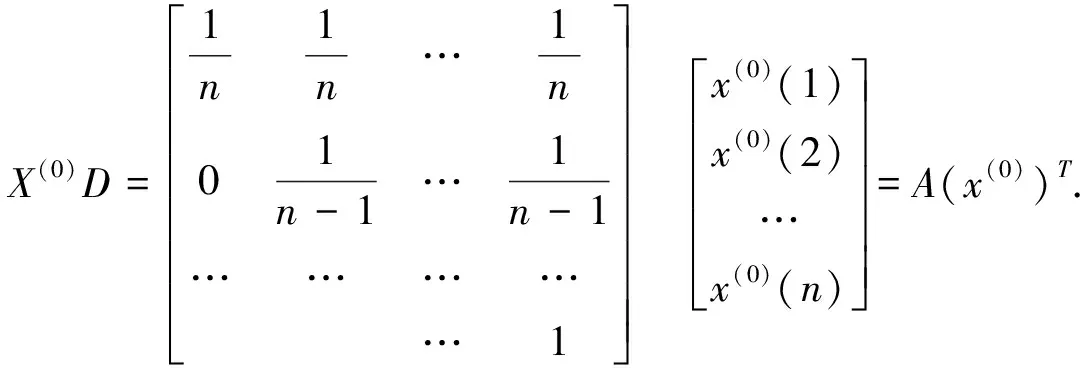
二阶弱化缓冲算子的矩阵形式为：

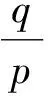
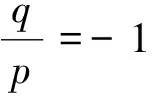
若X(0)为单调衰减序列，因为A(X(0))T≤(X(0))T，A为可逆矩阵，可得A-1A(X(0))T≤A-1(X(0))T，即(X(0))T≤A-1(X(0))T，所以D-1为单调衰减序列的强化缓冲算子；同理D-1为单调增长序列的强化缓冲算子。

若X(0)为震荡序列，x(0)(l)=max{x(0)(k)，k=1，2，…n}，x(0)(h)=min{x(0)(k)，k=1，2，…n}，

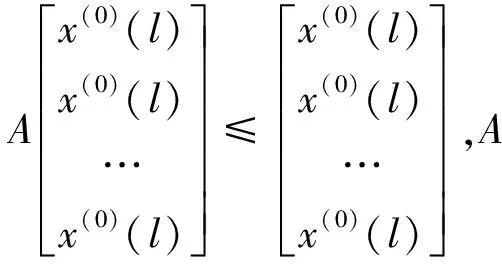
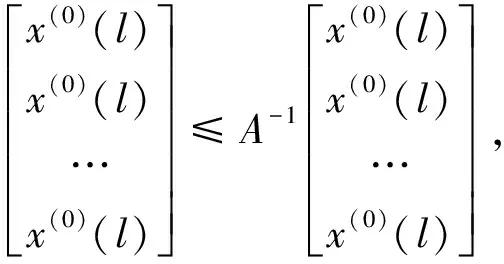
3 二次时变离散参数灰色预测模型介绍

对于实际应用的数据，因为受到外界诸多冲击因素的干扰而失真。为了能够准确的挖掘事物规律，针对以往模型使用连续时间响应式进行预测产生的跳跃性误差，本文使用时变参数离散灰色模型。

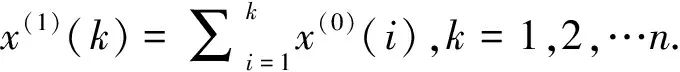
引理1 设x(0)(k+1)d1=(β1+β2k)x(0)(k)d1+β3k+β4为线性时变参数离散灰色模型，其中x(0)(k)为原始序列观测值，d1为经典弱化缓冲算子。

下面使用经典弱化缓冲算子d1作用后的序列建立二次时变参数离散灰色模型。

定义1设x(0)(k+1)d1=(β1+β2k+β3k2)x(0)(k)d1+β4k2+β5k+β6为二次时变参数离散灰色模型，其中x(0)(k)为原始序列观测值，d1为经典弱化缓冲算子。

定理1 对于二次时变含参离散灰色模型x(0)(k+1)d1=(β1+β2k+β3k2)x(0)(k)d1+β4k2+β5k+β6

该模型的最小二乘参数估计分别为：

为方便公示展示，记

因此有：

定理2 模型具有良好的性质：

(1)伸缩变换一致性

(2)白指数规律重合性

(3)能够完全模拟二次序列

(4)克服模拟值增长率恒定问题

(5)克服由连续响应式产生的跳跃性误差问题

证明过程不是本文重点，具体证明过程详见文献[3]。

二次时变离散参数灰色预测模型相比原有的一次时间项具有更高的预测值，在分数阶缓冲算子的参与下可以实现对模型的微调。

4 实例研究：不同分数阶预测结果比较

例1 以北京市年度科普经费筹集额为例，比较不同阶数经典弱化缓冲算子对模型预测结果的影响。原始数据见表1，数据来源中华人民共和国国家统计局。

表1 2008～2015年 北京市年度科普经费筹集额(万元)

取2008～2014年的年度科普经费筹集额为原始序列，分别建立0.6阶，0.8阶以及1阶经典弱化缓冲算子的二次时变参数离散模型，对2015年数据进行预测，预测结果及误差见表2。

由表2结果对比说明，0.6阶经典弱化缓冲算子可以实现模型的微调，拟精度较高，能较好的挖掘系统的发展趋势，得到比较好的预测精度。

表2 三种模型预测值与误差比较

例2 以我国江苏省科普专项经费为例，比较不同阶数经典弱化缓冲算子对模型预测结果的影响。原始数据见表3，数据来源《中国统计年鉴》。

表3 2008～2015年 江苏省年度科普经费筹集额(万元)

取2008-2014年江苏省年度科普经费筹集额为原始序列，同样建立了0.3阶，0.6阶以及0.8阶经典弱化缓冲算子的线性时变参数离散模型，对2015年数据进行预测，预测结果及误差见表4。

表4 三种模型预测值与误差比较

由表4结果对比说明，0.3阶经典弱化缓冲算子可以实现模型的微调，拟精度较高，能较好的挖掘系统的发展趋势，预测精度更好。

根据上面两个实例分析可以看出，分数阶的二次时变参数离散模型的预测精度更高，预测效果确实优于传统的整数阶模型。