基于碳排放考量的集装箱海陆多式联运模式选择

蒋玲茜+张培林+陈沿伊

【摘 要】 为使集装箱海陆多式联运模式选择能更符合节能减排的要求，分析碳排放影响因素并建立海陆多式联运碳排放计算模型和运输成本计算模型，在此基础上建立基于碳排放量、运输成本、运输时间的多目标决策模型，通过决策模型进行联运模式的比较选择。以哈尔滨市至泰安市的集装箱海陆多式联运为例，应用以上多目标决策模型得出“铁―海―铁联运”模式为最优方案。

【关键词】 集装箱；海陆多式联运；碳排放；多目标决策

0 引 言

交通运输行业碳排放量占各行业碳排放总量的30%以上，在节能减排日益重要的当今社会，推行低碳交通显得尤为重要和迫切。多式联运由于其降低成本、节能减排的效应显著，已被越来越多的国家纳入综合运输体系建设。对于集装箱多式联运来说，海陆多式联运是其最主要的联运方式，选择不同的联运模式会产生不同的经济效益和社会影响。以往在集装箱海陆多式联运模式选择的研究中，大部分学者[1-3]只是单纯考虑运输成本和时间这两方面因素的影响，较少有学者将碳排放这一因素考虑进去，即使有学者[4-5]对多式联运碳排放作研究也大多只是定性分析，较少有定量研究。在全球倡导低碳运输的大背景下，碳排放将成为海陆多式联运模式选择时必须考虑的因素。本文在前人研究的基础上，在集装箱海陆多式联运模式选择中加入碳排放这一因素，建立基于运输过程中碳排放量、运输成本、运输时间的多目标决策模型，并进行实证分析。

1 集装箱海陆多式联运模式

1.1 公海联运模式

公海联运是货物经由公路运至沿海港口码头，再经船舶运至目的地港口，或是货物经船舶运至沿海港口码头，再经公路运输至最终目的地的只需“一次申报、一次查验、一次放行”就可以完成整个运输过程的一种运输模式。[6]公海联运尽管不能达到运输成本最优且作业效率也较铁海联运低下，但由于其具有灵活性强、时效性高的特点，目前仍然是最主要的集装箱海陆多式联运模式。公海联运的整个运输过程中只涉及公路和海路2种运输方式。

1.2 铁海联运模式

铁海联运是货物经由铁路运至沿海港口码头，再经船舶运至目的地港口，或是货物经船舶运至沿海港口码头，再经由铁路运至最终目的地的只需“一次申报、一次查验、一次放行”就可以完成整个运输过程的一种运输模式。铁海联运与公海联运相比，铁海联运虽然在集货时间方面显劣势，但因有着巨大的运能、较高的作业效率、较少的废气排放、较低的成本等优势，已成为各个国家优先发展的一种运输方式。在铁海联运的整个运输过程中除了有铁路和海路运输方式外，还有从起运地到铁路集装箱场站以及从铁路集装箱场站到最终目的地的公路运输。

2 基于碳排放量、成本、时间的 多目标决策模型

2.1 海陆多式联运的碳排放计算

海陆多式联运的碳排放计算公式为

式中：W联为海陆多式联运每千米运输产生的碳排放量，kg； 海、 陆分别为海路和陆路运输里程在多式联运总里程中的占比； W海为海运段每千米运输的碳排放量，kg； W陆为陆运段每千米运输的碳排放量，kg。

本文只对同一起止点间进行不同的联运模式选择，由于公海联运和铁海联运中的海运段相同，因此，只要比較2种模式下陆路段的碳排放量即可。

在公海联运模式中，公路运输每标箱单位里程的碳排放量的计算公式为

式中：W公为公路每千米运输的碳排放量，kg； 汽为公路运输中汽油消耗量在燃料总消耗量中的占比；G汽为每标箱每千米运输所消耗的汽油量，根据相关研究[7-8]，G汽取0.689 L/（TEU€穔m）； F汽为消耗每升汽油所产生的二氧化碳，根据政府间气候变化专门委员会（IPCC）资料，F汽取2.27 kg/L； 柴为公路运输中柴油消耗量在燃料消耗总量中的占比；G柴为每标箱每千米运输所消耗的柴油量，取0.606 L/（TEU€穔m）；F柴为消耗每升柴油所产生的二氧化碳，根据IPCC资料，取2.74 kg/L。

在铁海联运模式中，由于我国目前营运的铁路机车绝大部分为电力机车，而电力机车虽然在行驶中不产生碳排放，但为其供电的发电企业是产生碳排放的；因此，在铁海联运模式中，铁路段每标箱单位里程二氧化碳排放量的计算公式为

式中：W铁为铁路段每千米运输产生的二氧化碳排放量，kg； G电为每标准集装箱每千米运输所消耗的电量，根据《中国交通年鉴》资料 G电取 kW€穐 /（TEU€穔m）； F电为上游发电企业生产每度电的二氧化碳排放量，F电=0.717 kg/（kW€穐）。

2.2 海陆多式联运的运输成本计算

海陆多式联运的运输成本是指整个联运过程中所需支出的全部费用，包括货物集散、在各个转运中心作业时所耗的场地租金、保险费和人工费用等。

本文只对同一起止点间的不同联运模式进行比较分析，由于具有相同的海运段，因此，在成本计算时只将公路运输段与铁路运输段进行成本比较。

2.2.1 公路运输成本计算公式

公路运输段每标箱的运输成本计算公式为

式中： C公为公路运输段每标箱运输成本，元； c1为公路运输中每标箱每千米的运输费，元； y为集装箱卡车的过桥费和过路费，元； l1为集装箱的卡车运输里程，km； a1为在集装箱堆场的装卸费，元； a2为集装箱卡车的出省费，元。

2.2.2 铁路运输成本的计算公式

铁路运输段每标箱的运输成本计算公式为

式中：C铁为铁路运输段每标箱的运输成本，元； c2为在铁路运输中每标准箱每千米的运输费，元；l2为铁路运输里程，km； E1为铁路建设基金率； e2为铁路运输相关均摊运费，元； b1为铁路运输的每标箱均摊发到基价，元； b2为集装箱使用费，元； b3为铁路发护费、联防费，元； b4为铁路场站装卸费，元； b5为施封材料费和组织服务费，元； m为与铁路运输相关联的公路运输费，元。endprint

3 实证分析

选取哈尔滨市至泰安市间海陆多式联运的不同模式，设定：一趟铁路班列装运80 TEU，每标准箱质量为10 t，其他基础数据如表1所示。

（1）得到各方案目标值

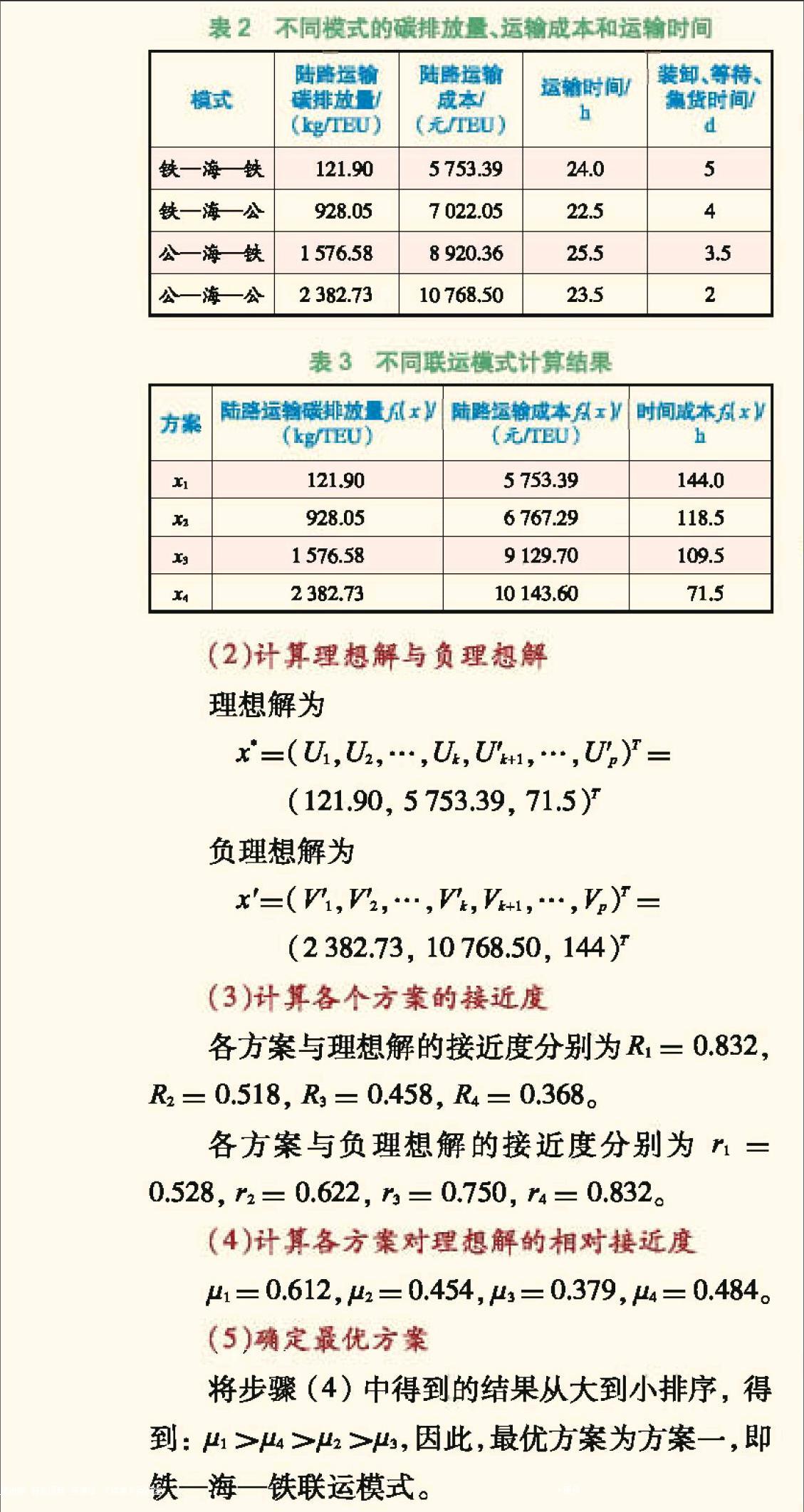
选取铁―海―铁、铁―海―公、公―海―铁、公―海―公等4种海陆联运模式，将式（1）―（5）中的相关量值取值如下： 汽= 20%；c1=6.5元/km； 哈尔滨―大连y=360元，烟台―泰安y=200元； a1=60元/km；a2=15元/km； c2=元/km；b1=161元/TEU；b2=100元/TEU； b3=4元/TEU； b4=386.1元/TEU； b5=65元/TEU； e1=0.528元/km； e2=元/km； m=900元。分别计算这4種模式中陆路运输碳排放量、陆路运输成本和装卸、等待、集货时间，见下表2。

根据多目标决策模型，计算得到4种方案3个目标的计算结果，见表3。

4 结果分析

本文实证案例中陆路运输段里程较长，因此，即使在铁路集货所需更多时间的情况下，得出的最优方案仍是铁海联运。根据本文所建立的运输成本计算模型可以得到每标箱的经济运距为320 km，即：运距小于320 km时公路运输成本低于铁路运输，运距超过320 km则铁路运输成本低于公路运输。若只考虑运输成本，则可直接比较运距。

根据碳排放量计算模型可以得到：公路运输段的碳排放量为1.641 kg/（TEU€穔m），铁路运输段的碳排放量仅为0.079 kg/（TEU€穔m），因此，在碳排放方面，铁路与公路相比有着很强的优势。

根据本文所建立的基于碳排放量、成本、时间的多目标决策模型，可以在不同情况下综合考虑碳排放量、运输成本和运输时间这三方面的影响因素进行集装箱多式联运的模式选择。

5 结 语

集装箱海陆多式联运具有运输成本低、效率高、低排放的优点，因此，我国现阶段应该大力发展集装箱海陆多式联运。从实证分析的结果可以看出，集装箱海陆多式联运在不同模式下其碳排放、运输成本和运输时间有差异，在全球倡导低碳经济的潮流下，在对其进行模式选择时不能仅考虑成本和时间，还应该考虑碳排放这一影响因素。

本文对集装箱海陆多式联运不同模式进行分析时在考虑成本和时间的基础上加入碳排放这一因素，使得分析结果更能体现节能减排的社会要求，更符合现代社会可持续发展的理念。本文以哈尔滨市至泰安市这一海陆多式联运线路为例，应用所建模型进行实证分析，结果表明该模型具有实用性及可行性，可以根据具体的情况给出相应的决策。在现实情况中，海陆多式联运的模式选择除了要考虑碳排放、运输成本和运输时间外还涉及很多因素，比如大气污染的治理成本、货主的要求等等，因此，在现有模型的基础上增加更多的影响因素来进行集装箱海陆多式联运模式选择是今后的研究方向。

参考文献：

[1] 乔欣宇.基于成本分析的多式联运运输方式选择研究[D].成都：西南交通大学，2015.

[2] 李愈，李美彦，赵军.基于运费结构的多式联运方式选择研究[J].铁道运输与经济，2011（11）：81-85.

[3] 韩增霞.集装箱多式联运路径及运输方式选择研究[D].大连：大连海事大学，2011.

[4] 魏众，申金升，黄爱玲，等.多式联运的最短时间路径―运输费用模型研究[J].中国工程科学，2006（8）：61-64.

[5] 施云清，罗贯三，李红.低碳经济条件下大力发展铁海联运势在必行[J].物流工程与管理，2010（9）：25-28.

[6] 孙家庆，张赫，宫晓婞.集装箱多式联运[M].北京：中国人民大学出版社，2016.

[7] 黄霏茜，林玉山.基于低碳经济的集装箱铁海联运效益分析[J].物流工程与管理，2011（9）：49-51.

[8] 孙国卿.铁海联运运量预测与效益研究[D].大连：大连海事大学，2010.

[9] 胡秦生.模糊多目标系统实用最优决策法及应用[J].系统工程理论与实践，1996（3）：1-5.

[10] 张守一.对一般均衡论和帕累托最优的新解释[J].经济问题，2010（11）：116-118.

[11] 盛昭瀚.最优化方法基本教程[M].南京：东南大学出版社，1992.endprint