欧氏空间中两两夹角相等的向量组的一些性质
2018-02-08凌雪岷潘娟娟
凌雪岷,潘娟娟,李 宁
(1.安徽新华学院通识教育部,安徽合肥230031;2.淮南师范学院金融学院,安徽淮南232038)
设n为任意正整数,如果把有序实数组(x1,x2,…,xn)叫做点,记作X;将所有这样的点X的集合叫做n维空间,又叫做n+1维空间中的“超”平面;把满足某种关系诸如不等式、方程(组)关系的有序实数集合叫做n维空间中的几何图形[1]。若对这样的点赋予线性性质与度量性质,则可以讨论n维欧氏空间中的有关问题。本文将解析几何和线性代数相结合,利用行列式和齐次线性方程组的若干性质[2],对平面解析几何中的向量角进行高维推广,研究欧氏空间En中两两夹角相等的向量组的性质,得到4个有意义的结论,为欧氏空间性质的进一步研究提供一定的理论基础,在一定程度上也说明了学科结合的证明方法在日常高等数学教学中的重要作用。
本文给出关于欧氏空间的相关定义和说明,其他未明确指出的参见文献[3-6]。
定义1[6]如果对n维向量,引进二维向量中定义的加法、数乘运算,则称此空间为n维向量空间(或线性空间),并记作Ln。
定义2[6]对于如上定义的n维向量空间Ln,引进二维向量中定义的内积,则称这样的向量空间为欧几里得空间,简称为欧氏空间,记为En(n≥2)。
定义3[6]在En中,n维非零向量之间的夹角规定为
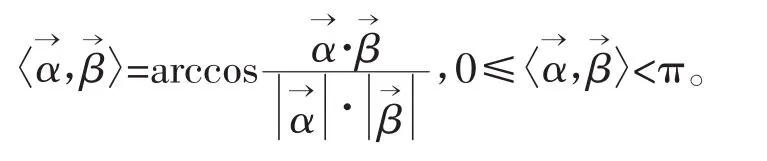
性质1 En中单位向量组两两成相等的锐角 θ=arccosσ1,其中,则线性无关。
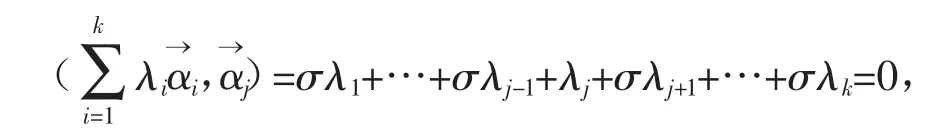
因此

记

由行列式的性质知,detD(σ)=(1-σ)k-1[1+(k-1)σ]>0,所以方程(1)只有零解,即λ1=λ2=…=λk=0,因此线性无关。
性质2 任意k≤n,En中存在单位向量,两两成相等的锐角θ=arccosσ2,其中σ2=
证明 由于D(σ)是正定实对称矩阵,故存在k阶实对称矩阵Pk,使得D(σ)=PkPkT。取En的一组基{ε1,ε2,…,εn},其中 εi=(0,…,0,1,0,…,0),令
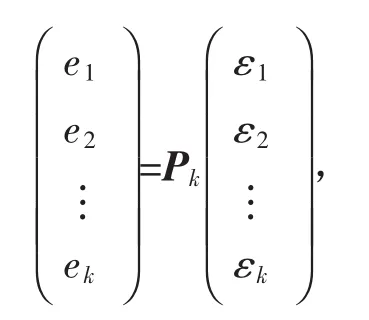
由于 dimV(e1,e2,…,ek)≤n 及{e1,e2,…,ek}线性无关,因此 k≤n。
性质3 En中至多有n+1个两两成钝角的向量。
证明 对欧氏空间的维数n进行归纳。
当n=2时,命题显然成立。
假设维数为n-1(n≥3)时命题成立,现证明对n维空间命题也成立。用反证法,设V中有单位向量组{e1,e2,…,en+1,en+2},(ei,ej)<0且1≤i≠j<n+2。
记 en+2生成的空间为 U,et=ξt+λten+2,ξt∈U⊥,λt∈R,1≤t≤n+1。于是
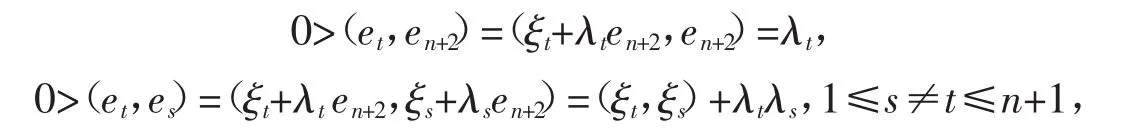
所以,(ξt,ξs)<-λtλs<0。这样,在n-1维空间U⊥中存在n+1个向量ξ1,ξ2,…,ξn+1两两成钝角,与归纳假设矛盾。
再证En中存在n+1个两两成钝角的向量。在V中取两两正交的单位向量组{e1,e2,…,en}组成一组基,在这组基下向量 α=x1e1+x2e2+…+xnen,其坐标为 α=(x1,x2,…,xn)。作
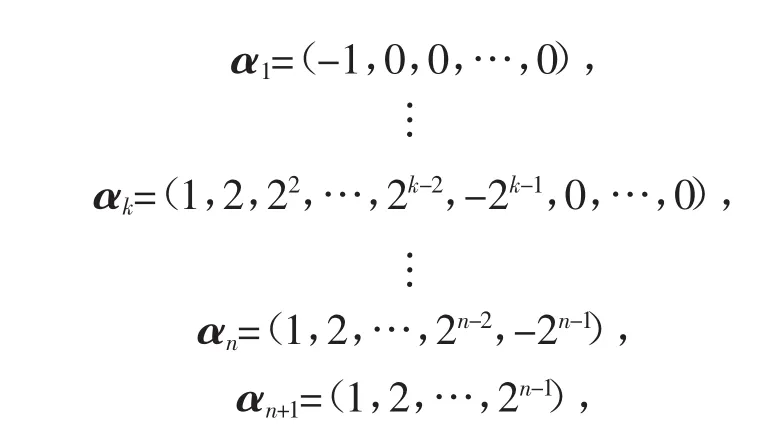
则

从而
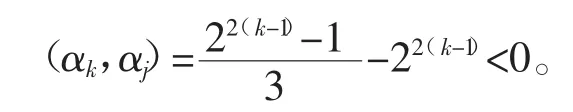
这就证明了用n+1个坐标αk代表的向量两两不共线且两两内积小于0,因此两两成钝角。
性质 4 En中存在 n+1 个单位向量{e1,e2,…,en+1}两两成相等的钝角且角度唯一。
证明 取 En中的一组基{ε1,ε2,…,εn+1},令
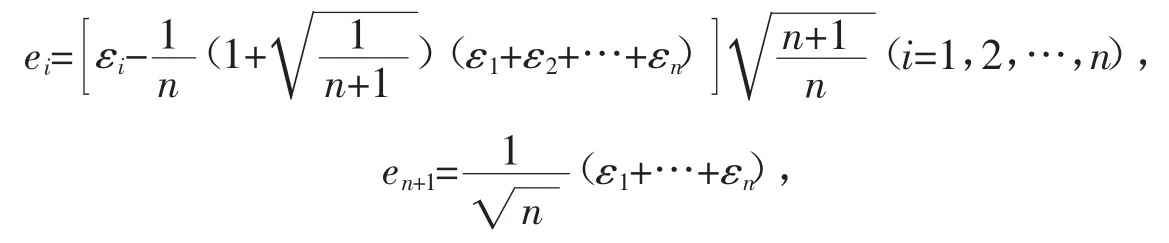
再证唯一性。设 En中单位向量组{α1,α2,…,αn+1}两两成钝角 θn',cosθn'=λ。取该空间的一组基{ε1,ε2,…,εn},设(α1,α2,…,αn+1)=(ε1,ε2,…,εn)P,P∈Rn×(n+1),则
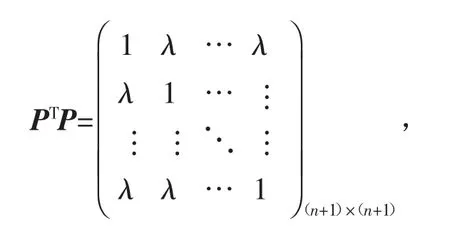
由于r(PTP)=r(P)<n+1,于是detPTP=(1-λ)n(1+nλ)=0,而-1<λ<0,得,即 θn'=θn。
鉴于平面解析几何的直观性和线性代数的抽象性特点,本文将解析几何和线性代数两门学科结合起来,利用行列式和齐次线性方程组的有关结论,研究了欧氏空间En中两两夹角相等问题,得出如下结论:
(1)两两夹角相等的向量组是线性无关的;
(2)En中存在 k(k≤n)个单位向量,它们两两成相等的锐角 θ=arccosσ2;
(3)En中至多有n+1个两两成钝角的向量;
(4)En中存在n+1个单位向量,它们两两成相等的钝角且角度唯一。
这些结论丰富了线性代数的内容,为后续的研究提供了一定的理论基础。
[1]陈志杰.高等代数与解析几何[M].北京:科学出版社,2002.
[2]李尚志.线性代数[M].北京:高等教育出版社,2011.
[3]北京大学数学系几何与代数教研室代数小组.高等代数[M].北京:高等教育出版社,1988.
[4]张禾瑞,郝丙新.高等代数[M].北京:高等教育出版社,1999.
[5]同济大学数学系.线性代数[M].北京:高等教育出版社,2016.
[6]沈文选.单形论导引[M].长沙:湖南师范大学出版社,2000.
