2017年高考文科数学全国卷(I)第12题的研究

广东省佛山市南海区教育发展研究中心(528200) 郑喜中

2017年高考文科数学全国卷(I)第12题是一道值得研究的好题.此题入门宽,解答方法多,有不同的运算路途和解法.通过不同的解法可以考查学生的思维层次.题目体现解析几何的思想,可化静为动,运用运动变化的思想解决问题.考查的知识点多,考查三角形的分割法,正切函数的定义,两角和正切公式,斜率公式,解二元二次方程组,根据椭圆的范围列不等式,运用均值不等式,参数方程等知识和数形结合的思想,分类讨论的思想,综合度大.如果运用直接法,考查运算求解能力和逻辑推理能力,能力要求高.

一、研究对象

题目1(2017年文科数学全国卷I第12题)设A、B是椭圆长轴的两个端点,若C上存在点M满足∠AMB=则m的取值范围是.

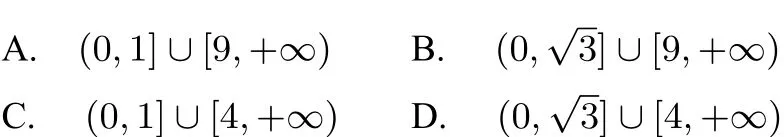
学生解决题目1的思路是将点M位置放在特殊位置.当m ＜ 3时,点M 落在y轴上,∠AMO=60◦,得m=1.当m＞3时,点M 落在x轴上,∠AMO=60◦,得m=9.

图1

图2

学生选择A,但是这种做法是不完整,得出的结论是靠猜测,没有达到考查的目的.因此题目1的选择支的设置有问题,可改进为

这样4个选择项均含有1和9,可避免学生利用极端情况猜得答案.

在解决题目1的过程中,学生如果知道如下的3个结论,可快速解决题目1.

结论1 在△ABM中,如果已知一边AB和它的顶角M为定值,顶点M的轨迹是圆弧.

结论2过点A(-3,0),B(3,0),M(0,1)的圆弧和椭圆的位置关系是圆弧上的点在椭圆内.

结论3当椭圆上的点M在短轴的端点上,M对椭圆长轴AB的张角∠AMB是最大.

对以上的3个结论说明如下:

说明1 建立坐标系,求点M轨迹方程得轨迹是圆弧,或者根据正弦定理也可知△ABM的外接圆的直径为定值,圆心位置是确定的,故知点M轨迹是圆弧;用此结论解决如下的

题目 (2013年高考新课标卷2理科第17题)△ABC在内角A,B,C的对边分别为a,b,c,已知a=bcosC+csinB.

(I)求B; (II)若b=2,求△ABC面积的最大值.

说明2画图3知圆弧在椭圆内部,

图3

证明 过点A,B,M的椭圆和圆弧的方程分别为:

在OB上任取一点G,过点G作垂线交圆弧和椭圆上的点,不妨设点(x,y1),y1＞0在椭圆上,点(x,y2)在圆弧上,代入方程得:

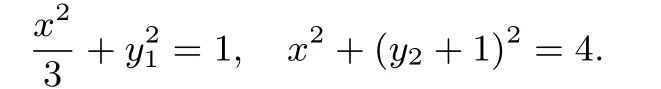
前式两端分别乘以3与后式两端分别相减得

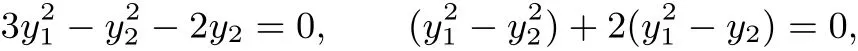
因为0＜y1≤1,所以+2(y1-y2),0＜ (y1+y2+2)(y1-y2);因为0＜y1＜1,0＜y2＜1,所以0＜y1-y2,y1＞y2.因此圆弧上的点在椭圆内.

说明 3 图4中,在圆弧上有 ∠AMB= ∠AFB,而∠AFB ＞ ∠AEB,所以 ∠AMB=∠AFB ＞ ∠AEB,

图4

点E在椭圆上,由此可看到当点E运动到点M处,点M对椭圆长轴AB的张角最大.

图5

如图5,知∠AEB ＜ ∠ACB＜ ∠AMB=120◦所以在椭圆上不存在点M 满足∠AMB=120◦.

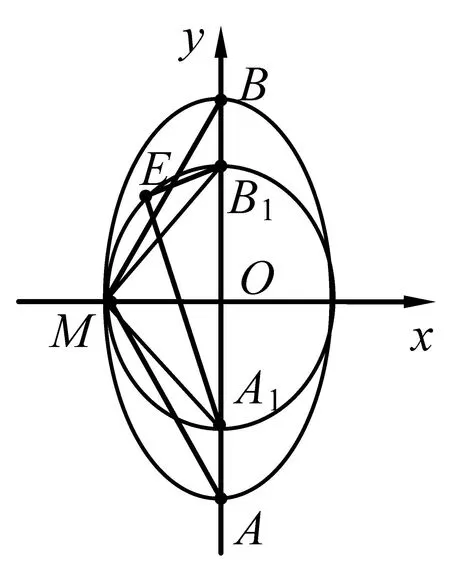
图6

直接法有三种解法,在后面对类似的问题——题目3作研究.

二、研究方法

2.1 题目溯源

题目2是在《高中数学解题题典》(主编李盘喜,东北师大出版社2001.5)P647中的一道题,题目2与题1极为相似.

2.2 学生测试

为了了解教师与学生对这一问题的认识,利用大规模的摸底考试,在2017年8月29日对我区2018届高三学生进行测试,测试题由课本例题和题1改编,如下:

题目3设点A,B的坐标分别为(-5,0),(5,0)直线AP,BP相交于点P,且它们的斜率之积是(0＜b＜5).

(I)求点P的轨迹方程;

(II)在点P的轨迹上有一点M且点M在x轴的上方,有∠AMB=120◦,求b的范围.

(II)(方法1)设点M的坐标为(x0,y0),过点M,作MH垂直于x轴,垂足为H,

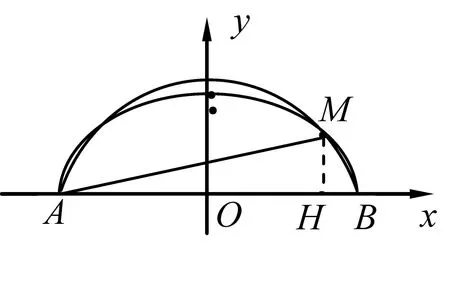
图7

因为点M 的坐标为(x0,y0)在点P的轨迹上,所以

②代入①得4

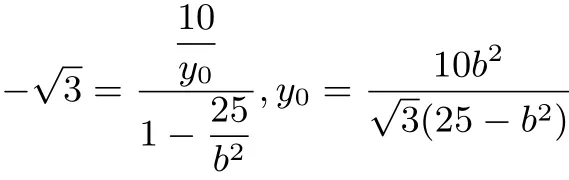
○代入③得

2.3 测试的结果

得分不理想,在1万多考生中没有满分.学生的主要错误有:没有画图就进行解题,不会运用数形结合的方法;不会运用条件∠AMB=120◦,不会对几何条件作代数化转换,如用斜率表示角,或者将三角形分割成两个直角三角形,而是运用余弦定理进行表示,造成运算困难而不能完成解决问题;没有说明为什么当椭圆上的点M在y轴上,点M对椭圆长轴AB的张角∠AMB是最大,思维不严密,对这一结果是猜测的.

2.4 教师讲评情况

教师对试题的评讲主要是讲了方法1和2,其实方法3更有一般性.教师在备讲评课时要对3种方法进行比较,看看哪种方法更让学生容易习得,了解学生不会做题的原因.题3的难点是学生不会运用题目的条件∠AMB=120◦.

为了了解评讲的效果,笔者在2018年9月16日再测试40位学生.测试题是:

◦1长轴的两个端点,若C上存在点M 满足∠AMB=120,求m的取值范围.

测试结果是2.5%的学生能正确解决题目4.说明学生的模型识别比较差,不会辨别题3与题4的关系.这与教师的评讲教学有关系,教师教学的针对性不强,对几何量的代数表征没有足够的重视,缺乏个性化的教学,对没有掌握的学生缺乏相应的帮助,没有让学生重做错题的习惯,也没有找出相关的题目评价教学的效果.如要看看此题的教学效果,看看如何用代数的方法表征角,用题目5让学生再练习,以达到教学的效果.

(1)(略); (2)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由.

三、结论

3.1 教师的教学

(1)选择“好”题进行教学 从题目溯源知在教学中的选材要选择有价值的题,选择“好”题进行教学,如教师在题海中,特别是在全国高考数学题中,筛选出能进行研究性学习的“好”题,这有利于提高尖子学生的水平.

(2)根据学生的作答情况进行教学 关注学生的答题情况,要了解学生不能作答的原因,是答题时间不够还是有足够的时间也没办法作出解答.如果是答题时间不够,在测试后让学生再独立完成作答;如果是无法作答,教师要研究学生存在的问题,并将题目的答案印发给学生自学,让学生看过答案后,再作答.教师根据学生的再作答情况进行评讲,这样能对学生开展个性化的教与学,也能提高学生的自学能力和数学的阅读能力.

(3)关注教学方法 评讲抓住解决问题的关键,教会学生运用题目的条件和挖掘题目中的隐含条件.教师要对题目中的多种解答方法进行比较,找出能使学生最容易掌握和习得的方法,在题3的第2问的解答中,方法3是最容易掌握的方法,且具有一般性,可以用此方法解决题6(将题2推广)、题7.

图8

(4)关注不同题型的不同解题策略和方法 教师要教会学生对待选择题与解答题的不同解题策略,选择题一般采用小题巧做的方法,解答题要注重思维严密,书写规范,教学中教师要有书写示范让学生学习书写表达.从上面可以看出,题1以选择题与解答题的形式出现,解答的方法是不同的.

(5)关注教学效果 要对教学的效果作检验,检查教过后,学生是否学会了,教学目标的达成度有多大.检查的方法就是给出相对应的练习题让学生再练习.

(6)深入研究试题,将试题作变式、推广.

(1)求∠AMB的范围;

(2)若∠AMB=120◦,求△AMB的外接圆的方程;

(4)是否存在椭圆C上的点M,使得它在x轴上的射影是椭圆的焦点,且∠AMB=120◦,若存在求出点M的坐标,若不存在,试说明理由.

3.2 学生的学习

(1)注意监控自己的解题策略,学会调整解题方向 学生要学会在解题过程中监控自己的解题策略,学会调整解题方向.不要一种方法做到底,如果此方法不能奏效,能否思考运用别的方法. 如部分学生运用余弦定理进行解答,而无法完成,主要受题目9这类题的影响,

题目9 F1,F2是离心率e1(a＞b＞0)的两焦点,点M 是椭圆C上的一点,∠F1MF2=120◦,求点M 的纵坐标.

(2)学会对比 学生学会根据自己(新手)的思考与教师(专家)的解答作对比,看看自己与教师的差别在什么地方,思考自我改进的方向和方法;

(3)关注错题 学生要坚持错题重做的策略.学生在学习中遇到困难,要有坚持的精神,可在教师的启发帮助下或者阅读教师提供的问题答案后再重做错题,直至会解决问题为止.

(4)学会提出问题 学生要学会提出问题,如在图3中,当点G在点O和点B位置时,|EF|=0.当点G在点O向点B运动时,|EF|不断变大,然后不断变小.因此通过观察图3学习提出问题:

题目10 在图9中过点A(-3,0),B(3,0),M(0,1)的椭圆和圆弧,在第一象限内过椭圆上一点F作x轴的垂线,与圆弧相交于E,试问|EF|是否有最值,若有求出最值.

图9

解答 过点A,B,M的椭圆和圆弧的方程分别为:

总之,数学教学中对一道题的研究,一般是研究题目考查的知识目标和能力目标,研究教学方法,研究如何让学生学会,分析学生是否具备解决问题的数学活动的基本经验,重点培养学生阅读数学材料的能力,调动学生的学习积极性.在关键的地方给学生以帮助,重视教后检查学生学习的效果.教师能对问题从多层次多角度提出新的问题,教会学生提出问题和解决问题.