例谈恰当分离策略在压轴题中的应用

广东省佛山市第一中学(528000) 陈豪

本文通过对几道高考题、高考模拟题解题思路的探究、比较、分析,旨在寻求含lnx与ex的组合函数压轴题的一般性的解题思路和解题策略.近年来诸如此类的问题一直是全国卷的考查热点,如2011年全国卷21,2013年新课标文20,2014年新课标1理21,2015年新课标1文21,此类题型注重理性思维和创新意识的考查,往往综合性强,思维强度大,方法性强而灵活,解题突破口不易找寻,常常需要适当变形转化求解,对数学思维能力的要求相当高.本文通过举例具体说明在解决函数恒成立、不等式证明、求解函数零点个数等问题中,恰当分离参数或分离函数的解题策略在解题中的实际应用.

一、恰当分离策略在恒成立中的应用

例1(2015年武汉模拟)设函数f(x)=1-x2+ln(x+1).

(1)求函数f(x)的单调区间;

分离 方式一 直接分离参数

由x0∈(2,3),知x0+1∈(3,4),所以k的最大值为3.

分离 方式二 线性分离方式

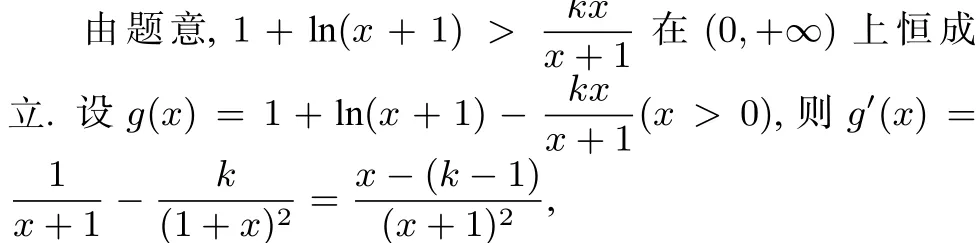
(1)当 k=1 时,则 g′(x)=＞ 0,所以g(x)单调递增,g(0)=1＞0,即g(x)＞0恒成立.

(2)当k＞ 1时,则g(x)在(0,k-1)上单调递减,在(k-1,+∞)上单调递增,所以g(x)的最小值为g(k-1),只需g(k-1)＞ 0即可,即lnk-k+2＞ 0.设h(k)=lnk-k+2(k ＞ 1),h′(k)=＜0,则h(k)单调递减,因为h(2)=ln2＞0,h(3)=ln3-1＞0,h(4)=ln4-2＜0,所以k的最大值为3.

分离 方式三 恰当分离方式 (尽量分离成下面8中形式或者其变式.)

图1

只需要研究k＞ 0相切时即可,设切点为(x0,y0).在切点处有两条曲线斜率相等,函数值相同.所以代入消去x0,有lnk-k+2=0.k∈N.

由上可知,k≤3.

评注 上述三种分离方式都可以解出k≤3,我们要关注的是哪种方式学生有可能做得出来,方式一中采用了直接分离参数,分离后的函数较大,求导比较繁琐,需要二次求导,方式二,则是线性的分离,函数式子还是较大,相对好一些,也需要讨论,而方式三,则是转化为两个更简单的基本函数,通过数形结合的方法,容易观察出两个函数相切的临界情况即为所求.在一个普通高中,学生基础比较薄弱的时候,前两种方式函数式复杂,学生看到就不愿动手,实现难度大,第三种方式可以化繁为简,变成两个简单的函数,学生容易入手,我们可以尝试引导这种方式去讲解.下面我们由重要函数不等式ex≥x+1,lnx≤x-1可以演变出下面几种基本函数模型及相应的函数图像,值域,以供参考.

二、基本函数归纳与迁移

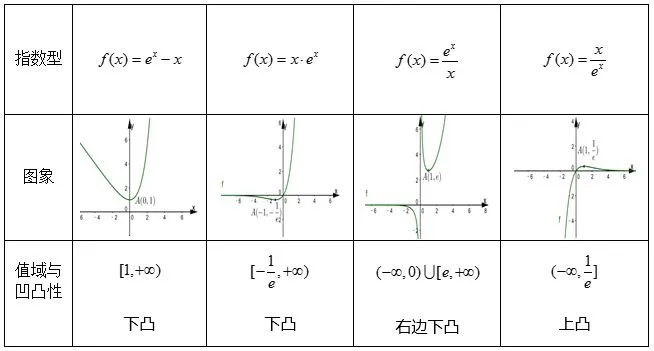
同种图像可以对比去观察变化趋势

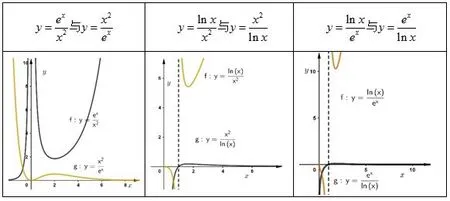
学生做题最怕遇到陌生情景,往往难于找到突破口,容易钻牛角尖,盲目探究、浪费大量时间,最后总是半途而废,没有坚持下来,老师上课往往是引导学生将陌生情景转化到熟悉的、学过的场景.学生如果知道哪些函数是可以求出值域,哪些是比较难求的,他们在做难题时感觉有做出来的希望,就有信心去挑战,坚持实现,最后思维力就逐渐提升.由上述的8种基本情况,我们还可以对它们进行变形迁移,是学生能够解决更多这种类型的问题.

迁移1自变量次数不同或者整体形式类似.

迁移2部分自变量加上常数

如:f(x)=xex+m,值域为 [f(-1),+∞);f(x)=(x+m)ex,值域[f(-m-1),+∞).

迁移3与一次函数相加求得值域

xe+bx+c(b＜0)值域为[f(ln-b),+∞);f(x)=xlnx+bx+c值域为[f(e-b-1),+∞);f(x)=xex+bx+c(b＜0)值域为:[f(x0),+∞),其中(x0+1)ex0+b=0.其它的也可以类似地求出.

迁移4与二次函数相乘求得值域

若 f(x)=ex(ax2+bx+c),f′(x)=ex(ax2+(2a+b)x+b+c).当 ∆ =(2a+b)2-4a(b+c)＞ 0时,设x1,x2(x1＜x2)是方程ax2+(2a+b)x+b+c=0的解.若f(x2)＞0,则函数值域为(0,+∞),若f(x2)≤0,则函数值域为[f(x2),+∞).当∆ =(2a+b)2-4a(b+c)≤0,则函数值域为(0,+∞).

迁移5与二次函数相加求得值域

或a=0讨论可以求出值域,读者可以有其他更多迁移.

三、恰当分离策略在不等式证明中的应用

例2 (2014年全国理科第21题)设函数f(x)=aexlnx+,曲线y=f(x)在点(1,f(1))处的切线为y=e(x-1)+2.

(1)求a,b;

(2)证明:f(x)＞1.

评注 这一题比较经典,很多老师都引用了这个例子,而且这题还可以通过重要不等式的放缩可以快速证明,文[1]蓝老师提出了两端构造,各个击破,观点正是恰当分离策略中的一种,文[3]中曾老师的间接“构造函数”视角也有类似讲解,注意在证明像上述的不等式时,必须要有g(x)min＞h(x)max作为前提,才能得到g(x)＞h(x),两者并非充要条件,否则不能得到g(x)＞h(x),这种方法有一定的局限性学生要理解透.

(1)求k的值.

(2)求f(x)的单调区间.

(3)设 g(x)=(x2+x)f′(x),其中 f′(x)为 f(x)的导函数.证明:对任意x＞0,g(x)＜1+e-2.

令导易求h(x)max=h(e-2)=1+e-2,求得φ(x)min=φ(1)=1+e-2.因为h(x)max=h(e-2)=1+e-2≤ φ(x)min,又这两个函数取得最值时的自变量取值不同,所以h(x)max=h(e-2)=1+e-2＜φ(x)min.所以1-xlnx-x＜通过求1+e-2.

评注 本题也有其它的构造方法,如文[2]中黄老师是采用的g(x)=h(x)φ(x),引出这个例子,就是希望学生在遇到以后代数式中既遇到lnx又遇到ex时可以将这两个函数放到不等号两边构成两类熟悉的基本函数,再来求其值域.

四、恰当分离策略求零点个数问题

例4已知函数f(x)=klnx-x2,k∈R.

(1)若f(x)在(0,1]上是增函数,求k的取值范围;

(2)讨论函数f(x)的零点个数.

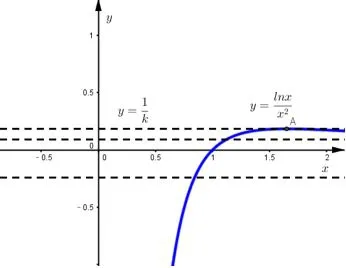
图2

图3

评注 这一题还有一种方法可以通过看原函数的极值的正负讨论出零点的个数,通过分离函数,可以很形象地看出交点个数的范围,引用这个例子主要是引导学生观察函数式的结构特征,类似上面8种基本函数或者它们的变形上去转化,如果有多种方式转化,还要考虑选取哪一种更为合适,讨论时更方便,上例中可以看得出,方式一分理后的函数更简单,后者函数有两段,有些学生大意会遗漏.

恰当分离策略在恒成立,不等式或者零点应用的实质一般要满足两点,一是转化到凹凸性不同的两个函数,二是转化到可以求出最值的基本函数.例如例2(2014年全国理21)中转化为图4中下凸的y=xlnx以及上凸的如果转为为图5中的下凸的y=xex,以及局部下凸的则凹凸性不同不能直接比较最值来求,而且右边最值也难求.

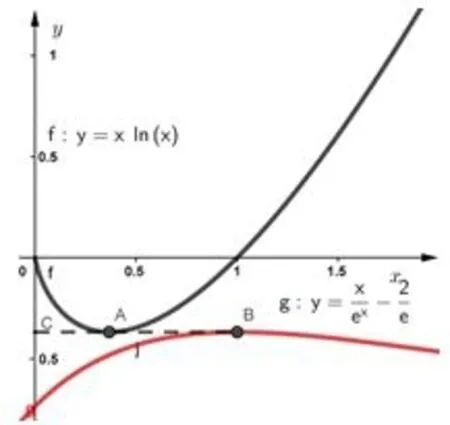
图4

图5

总之,零点问题、证明或解复杂的不等式(包括不等式恒成立或存在性问题)等函数压轴题,常常采用分离参数或分离函数的策略,最终还是化归为构造函数,再利用导数研究相应的性质,充分发挥导数的工具性和应用性的作用,往往可以获得问题的解决！因此,在复习中,教师要注意详细剖析解题思路的发现,强化转化意识,注重分类讨论,强化构造函数解决问题的通性通法.

[1]蓝云波.也谈构造函数、利用导数解答不等式恒成立问题[J],中学数学研究,2016(5):31-33.

[2]黄俊峰.例谈高考函数中的构造[J],中学数学研究,2016(5):26-28.

[3]曾辛金.一道高考数学模拟题的多视角解析*[J],中学数学研究,2016(5):18-21.