对一道高考题的反思与探究

湖北省广水市第一高级中学(432700) 聂文喜

在近年高考及全国各地模拟考试中,频繁出现以共焦点的椭圆与双曲线为背景的两离心率之积与两离心率倒数之和的最值与范围问题,学生面对此类问题往往束手无策,本文通过一道高考题探究与此类问题有关的三个优美结论,通过具体例子并说明结论的应用.

题目 (2016年高考浙江理科第7题)已知椭圆C1:n＞0)的焦点重合,e1,e2分别为C1,C2的离心率,则( )

A.m＞n且e1e2＞1 B.m＞n且e1e2＜1

C.m＜n且e1e2＞1 D.m＜n且e1e2＜1

解 设P为椭圆与双曲线在第一象限内的公共点,F1,F2为它们的公共焦点,则|PF1|+|PF2|=2m,|PF1|-|PF2|=2n,所以|PF1|=m+n,|PF2|=m-n,所以m＞n,

反思1 本题中椭圆短半轴与双曲线的虚半轴相等,椭圆离心率与双曲线离心率之间等量关系式为如果对任意两个共焦点的椭圆与双曲线,那么椭圆与双曲线的离心率有何等量关系式.

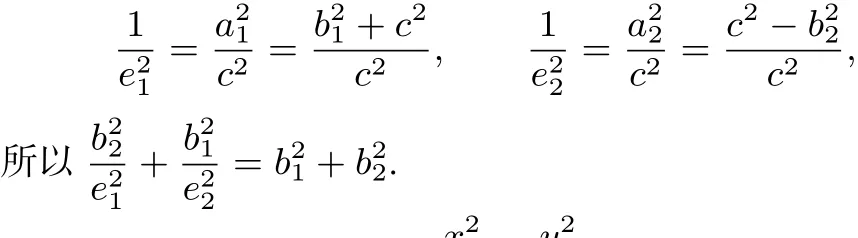
反思2 本题中椭圆短半轴与双曲线的虚半轴相等,椭圆与双曲线的离心率之积的取值范围为(1,+∞),如果对任意两个共焦点的椭圆与双曲线,那么椭圆与双曲线的离心率之积的取值范围是否为(1,+∞).

反思3若将椭圆和双曲线的离心率之积改为椭圆和双曲线的离心率倒数之和,是否有相应的结论呢?

例1(2016年全国高中数学联赛(四川初赛))已知F1,F2为椭圆和双曲线的公共焦点,P为它们的一个公共点,且∠则该椭圆和双曲线的离心率之积的最小值是( )

例2(2014年全国高中数学联赛湖北赛区预赛第10题)记共焦点的椭圆与双曲线的离心率分别为e1、e2,若椭圆短轴长是双曲线虚轴长的2倍,

例3(2014年高考湖北理科第9题)已知F1、F2是椭圆和双曲线的公共焦点,P是它们的一个公共点,且∠FPF=,则椭圆和双曲线的离心率的倒数之和的最大

12值为( )

通过对高考题的反思与探究,不仅对解题过程有较为全面的认识,还可以使试题的内涵与处延得到深入挖掘与拓展,从而达到做一题、通一类、会一片,真正实现在反思中探究,在探究中提升学生的思维与创新能力.