q-Kampé de Fériet函数的简化和求和公式
2018-02-05刘红梅秦艳杰
刘红梅, 秦艳杰
(大连民族大学 理学院,辽宁 大连 116650)
1 预 备
对|q|<1,基本超几何级数定义为[1]
式中:bj≠q-n(j=1,2,…,s),(x1,x2,…,xr;q)n=(x1;q)n(x2;q)n…(xr;q)n为升阶乘乘积,其中的因子为升阶乘,定义为
q-Kampé de Fériet函数是Kampé de Fériet函数的q-模拟,是双变量基本超几何级数,在1985年由Srivastava和Karlsson给出定义[2]
式中:|x|<1;|y|<1;|q|<1;i,j,k∈0。当λ=μ=r=s=1,u=v=0时,
式中:Φ(1)为相对常见的第一类q-Appell函数见文献[1]283和[3]232。

2 基于Jackson变换的简化公式
Jackson变换公式为
(1)
定理1Ω(m)为任意复数序列,假设下列级数都绝对收敛,有变换公式
(2)
(3)
证明利用式(1),计算式(2)

(4)
在式(4)中,令m+n=N,化简,可推导出式(3)。
推论1 假设下列级数都绝对收敛,有关q-KampédeFériet函数的简化公式成立。

(5)
(6)
证明在定理1中,令Ω(m)=1,由q-二项式定理(见文献[1]中公式(1.3.2))得
(7)
可得计算式(3)的内部求和公式为
经过化简可以得到简化公式(5)。
(8)
计算式(3)的内和,经过化简立即可得公式(6),这个公式正好是文献[9]中公式(2.2)的q-模拟。
3 基于Heine变换的简化和求和公式
在这一节中,通过应用Heine的三个变换公式,又建立了三个一般的双重q-级数变换和一些简化公式。
首先,将定理1证明中的Jackson公式(1)替换为Heine变换公式(见文献[1]中公式(1.4.1),也可见文献[10]中公式(E3.1a))
得到级数变换公式定理3。
定理2 对于任意复数序列Ω(m),假设级数都绝对收敛,则

(9)
推论2 假设级数都绝对收敛,有求和与简化公式
(10)
(11)
(12)
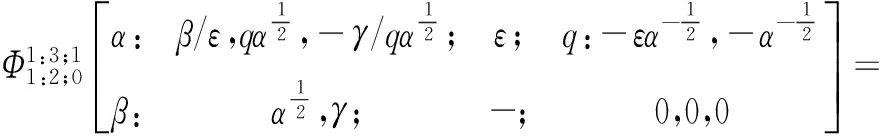
(13)

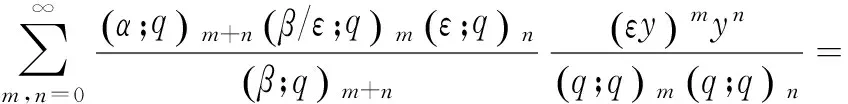
最后一个等式是来自q-二项式公式(7),求和公式(10)得证。
定理2中令
并通过q-Pfaff-Saalschütz求和定理(见文献[1]中公式(1.7.2))得
对式(7)中内部的和式进行计算,然后进行一些化简,得到简化公式(11)。
在定理2中令
然后利用求和公式(见文献[1]中例2.14)
(14)
计算式(9)中内部和式,推导出另一个简化公式(12)。另外,在定理2中令
并用公式(见文献[1]中公式(3.10.9))
(15)
计算式(9)的内部和式,得到了式(13)。
式(10)等号右边的式子与参数β和ε无关,这个求和公式可以在式(5)中直接令x=εy获得。
其次,运用Heine的q-欧拉变换 (见文献[1]中公式(1.4.3)或文献[1]中公式(E3.1c))得
(16)
有如下双重q-级数变换公式。
定理3 对于任意复数序列Ω(m),设级数都绝对收敛,有
(17)
(18)
证明重新计算式(17),

运用公式(16),并经过一些化简,可得式(18)。
推论3 设级数都绝对收敛,有简化公式
(19)
(20)

最后,给出第三个Heine变换(见文献[10]中公式(e3.1b)),
(21)
类似于定理2和定理3的证明,通过Heine变换式(21),得到了第三个变换公式。
定理4 对于任意复数序列Ω(m),设级数都绝对收敛,有
(22)
(23)
推论4 设级数都绝对收敛,有
(24)

(25)
(26)

然后经过一些化简,得到简化公式(24)。
在定理4中令
在式(23)中分别利用式(14)和(15),可以得到另外两个简化公式(25)和(26)。
[1] GASPER G, RAHMAN M. Basic Hypergeometric Series [M]. second ed., Cambridge: Cambridge Univ. Press, 2004.
[2] SRIVASTAVA H M, KARLSSON P W. Multiple Gaussian Hypergeometric Series [M]. New York: Halsted Press, 1985.
[3] SLATER L J. Generalized Hypergeometric Functions [M]. Cambridge: Cambridge Univ. Press, 1966.

[5] JIA C Z, WANG T M. Reduction and transformation formulae for bivariate basic hypergeometric series [J]. J. Math. Anal. Appl., 2007, 328: 1152-1160.
[6] CHU W C, JIA C Z. Transformation and reduction formulae for doubleq-Clausen hypergeometric series [J]. Math. Methods Appl. Sci., 2008, 31: 1-17.

[8] LIU H M, WANG W P. Transformation and summation formulae for Kampé de Fériet series [J]. J. Math. Anal. Appl. , 2014, 409: 100-110.
[9] CVIJOVIC′D , MILLER A R. A reduction formula for the Kampé de Fériet function [J]. Appl. Math. Lett., 2010, 23:769-771.
[10] CHU W C , CLAUDIO L D. Classical Partition Identities and Basic Hypergeometric Series [M].Lecce-Italia: Università di Lecce, 2004.
