一种基于传感器网络的水污染源质心定位算法*
2018-02-05吴晨晖
罗 旭,杨 君,吴晨晖,冯 政
(1.遵义医学院信息工程学院,贵州 遵义 563000;2.武汉科技大学信息科学与工程学院,武汉 430081)
传感器网络具有覆盖区域广、自组织、不受地理位置限制等优点[1-2],常用于环境监测。目前基于传感器网络的污染源定位算法无论是关于气体污染源还是水污染源,多根据污染物的迁移过程,基于扩散模型进行定位。例如文献[3-12]中,在各类具体扩散情形和扩散模型下研究了污染源定位问题,其中文献[9-12]探讨了水污染源定位问题。在此类定位算法中,主要基于污染监测数据,根据扩散模型,建立含有污染源位置的参数估计模型,并采用最小二乘、贝叶斯估计、状态滤波等方法求解估计问题。在基于扩散模型的污染源定位算法中主要有两大问题:①在求解基于扩散模型的数学问题中常涉及到复杂的数值计算,近似数值计算引入了参数估计误差。②扩散模型本身是在较为理想的条件下提出的,并不能精确描述扩散过程本身,因此扩散模型本身引入了定位误差,并且在某些情形下并没有解析扩散模型,基于扩散模型的解析类定位算法并不能适用。
尽管目前也有一些不依赖于水文模型的水污染源定位算法,如最接近点算法(CPA)[13],最大监测点算法(MPA)以及最早探测点算法(EPA)[14]。此类算法中,污染源位置为网络内某节点的位置,定位精度依赖于节点部署密度。当监测区域较广例如湖区、河流中,由于节点难以密集部署,算法精度不高。此类算法属于粗略定位算法。
在水污染事件中,及时发现污染源并进行处理十分重要。考虑到已有水污染源定位算法的上述问题,提出了一种基于传感器网络的水污染源质心定位算法。该算法虽然与扩散模型无关,但依然结合了水污染扩散规律解决定位问题。该算法仅依赖于传感器网络的监测数据,关键在于根据水污染扩散特征以及浓度场等位线求得污染源位置。相对于以某节点的位置为污染源位置的定位算法,该算法分析了监测数据,不属于粗略定位算法,受网络节点部署位置和密度的影响小;相对于基于扩散模型的定位算法,该算法即利用了监测数据,又避免了浓度模型和复杂的数值计算给污染源定位带来的负面影响,并可用于无解析浓度模型的场景中。
在下文中,首先给出该质心的算法的一般性问题,然后给出求解方法。
1 问题描述
1.1 问题背景
根据污染物迁移过程来估计污染源位置是污染源定位的基本方法,而污染物的扩散过程是污染物迁移主要过程。本文的质心算法主要依据水体中二维扩散过程求取污染源的平面位置。本文的污染源估计问题即根据已知的传感器网络节点在各采样时间的浓度监测信息C(xi,yi,tl),节点位置以及不同节点的探测时间Ti,i=1,2,…,n来求取污染位置。并且本文的质心算法有以下3个前提假设:①监测区域中只有一个污染源。②节点越早探测到污染信息,离污染源越近。③污染源位置的边界条件已知,即(x0,y0)∈B已知。
1.2 网络部署
在监测区域中均匀分布有I(>5)个传感器节点。传感器节点位置固定,待测污染物类型已知,伸入水下的探测传感器给定。传感器节点位置已知,所有的传感器节点以同一采样周期同步采样并存储数据,监测数据路由到汇聚节点并送往数据中心进行处理。
1.3 质心定位问题
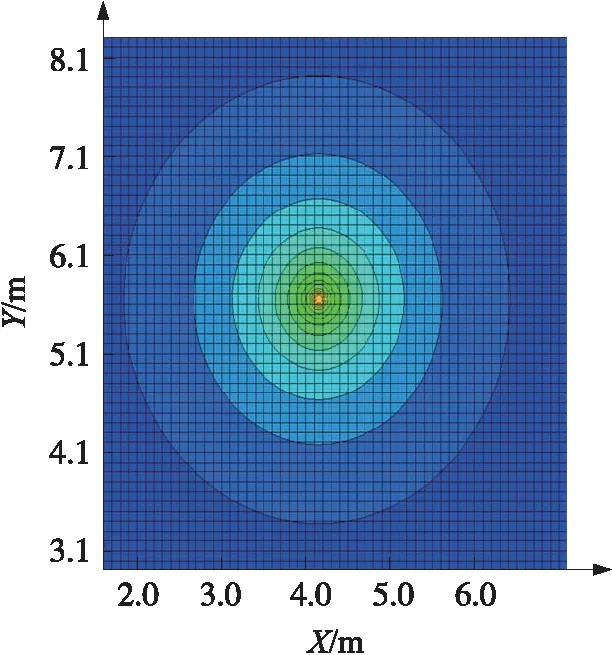
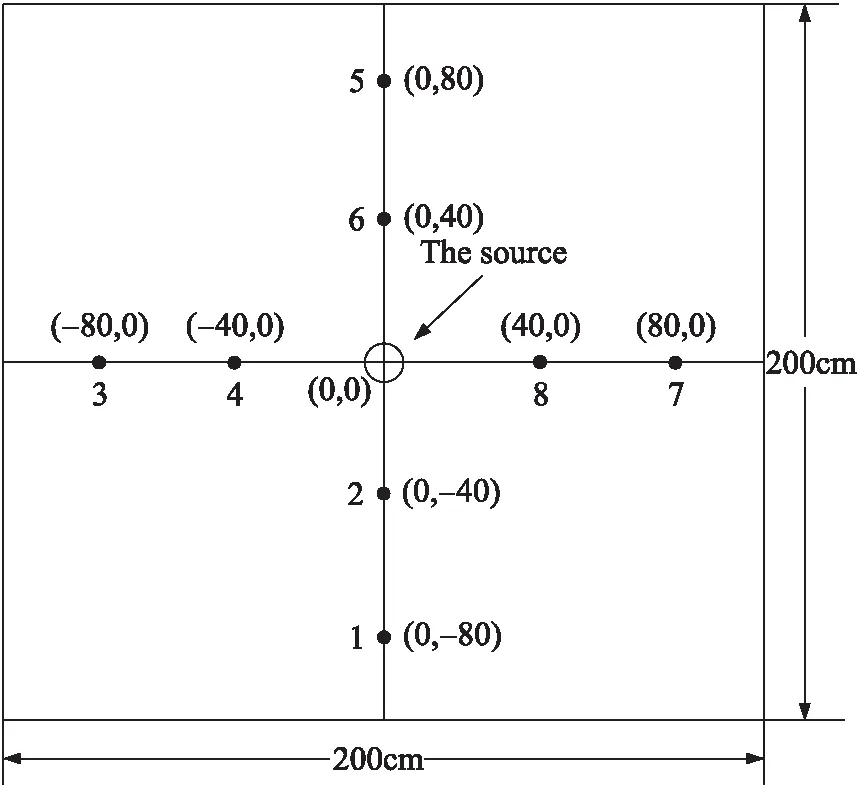
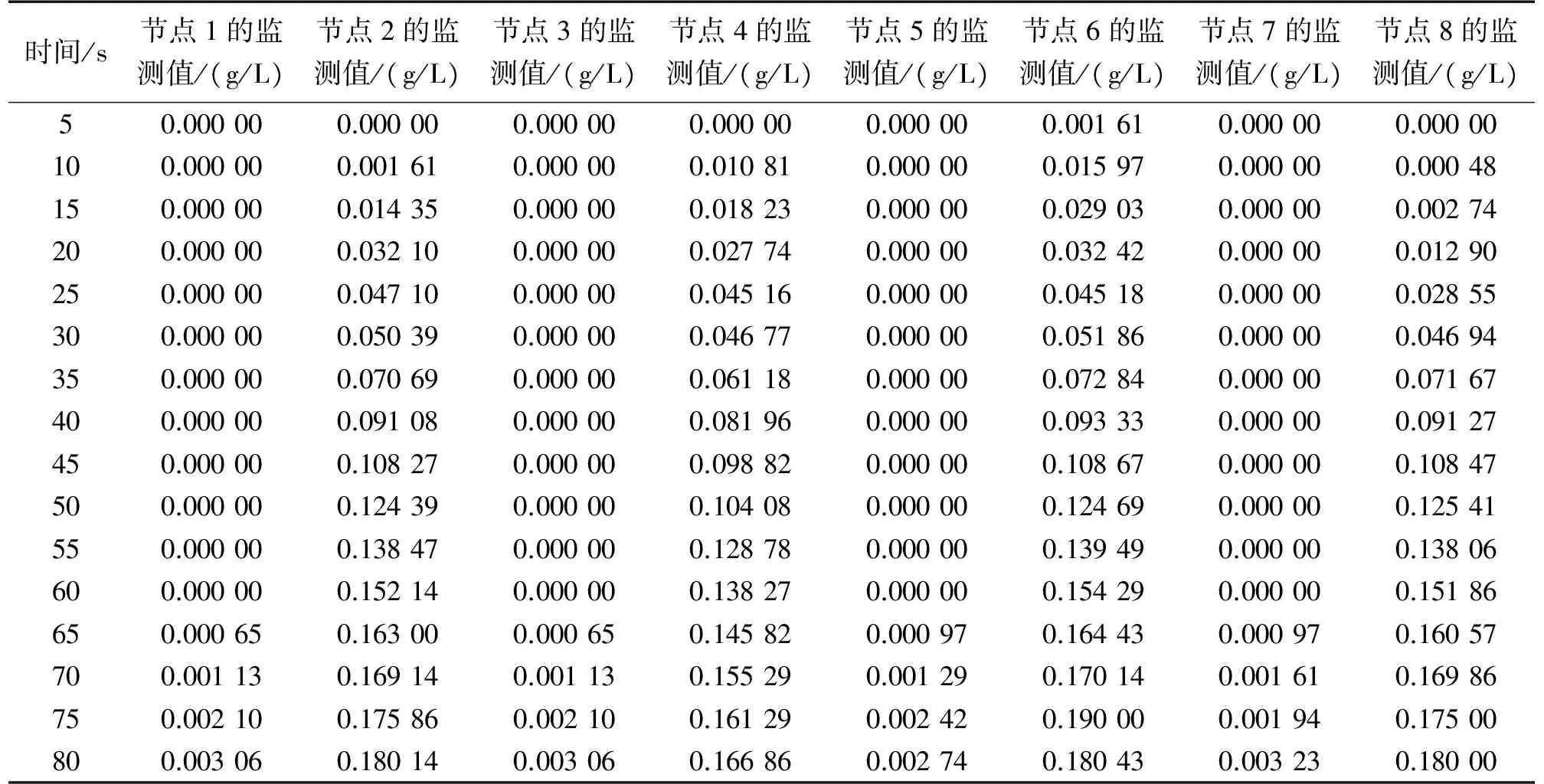
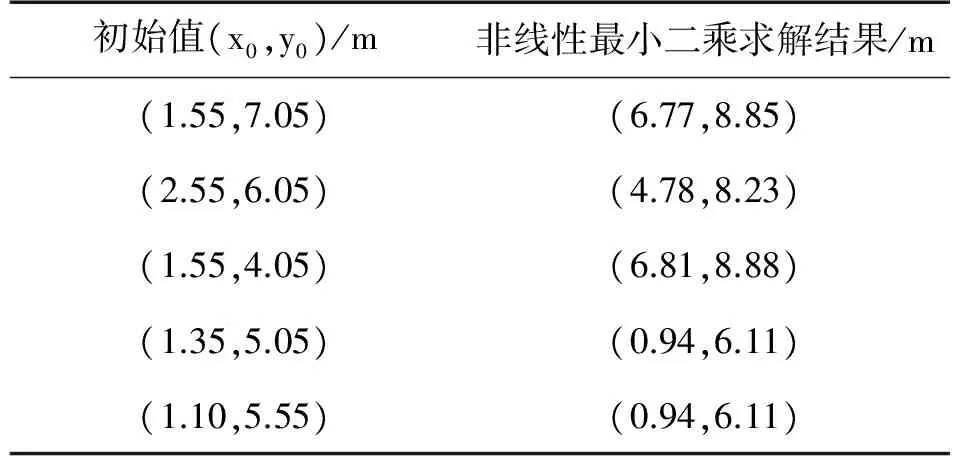
将(xi,yi,Ti),i=1,2,3,…,I按节点的污染探测时间Ti排序,使得T1 (1) 式中: D= D可简化为 (2) 是由直线 围成的区域。 若有多个节点同时且最早发现污染源,例如T1=T2 D= (3) 即有n个节点同时且最早探测到污染时,有n组不等式。 在上述定位方法中,首先是找到最早发现污染的节点(x1,y1),然后是计算式(1)中区域D的质心。式(1)没有解析解,需要通过几何方法求解。但在许多情形下,由于水污染扩散场中存在浓度场等位线,可依此获得解析解。在下文中将首先给出存在浓度势场等位线下的解析解,然后介绍相关的数据预处理,包括污染探测和浓度等位线检验。 图1 具有圆形等位线的浓度场 Case 1 节点有同一污染探测时间并在圆形等位线上 如图1所示,在不受边界限制的扩散场中,浓度等位线呈圆形。在此情形下,在同一等位线上的节点(xi,yi),i=1,2,…,I到污染源的距离相同并在同一时间探测到污染。可得: (4) 并可写为 (x1-x0)2+(y1-y0)2=r2 (5) 其解为 (6) 式中: Case 2 节点有同一污染探测时间并在轴对称等位线上 如图2所示,扩散受边界Y影响,污染源位置在等位线的对称轴上。 (7) 根据式(2),同时可得: (8) 以及估计: (9) 图2 具有对称等位线的浓度场 记: X={(x1,y1),(x2,y2),…,(xI,yI)}:传感器节点集合; N(X):X中节点的数量; N(X′):X′中节点的数量。 2.2.1 污染探测 ①简单探测法 ②基于假设检验的探测法 当监测数据变化缓慢,且浓度值较小时,采用该方法。由于监测数据在大多数情况下是非正态的,采用Wilcoxon秩和检验法[15],即检验表1中两组独立数据是否有显著差异。 表1 探测中的两组独立样本 假设为: (10) 式中:μs1与μs2为样本组1和样本组2的平均值。 将样本组1和样本组2中的数据一并升序排列,并依序标记数秩[15]。当检验显著性水平为α,样本组1中数据对应的秩和为R1,若 R1≤CU(α/2) (11) 2.2.2 浓度场等位线检验 判定在X′中的节点在环形等位线上,否则这些节点在各轴对称等位线上,这里χ为经验参数。 首先,本文算法是单源定位算法,式(1)的定位算法适用于所有情形,当有足量的节点处于浓度等位线上,至少满足N(X′)≥max{(N(X)/4,4}时,可依据式(6)~(9)利用等位线上的节点数据得到解析定位结果。 再次,本文算法主要结合平面浓度等位场讨论定位问题。值得指出的是,在三维扩散中当扩散系数各向同性时为等位球面,质心算法尤其是基于浓度等位线的质心定位可推广使用,这方面的内容将在后续的工作中讨论。 实验1:静态水体中不受边界限制的浓度场中的污染源定位。 问题背景:在浅滩水体中,水域大小为200 cm×200 cm,水深f=100 cm。在水域中心有一连续(污染)源。自t0=0 s起MgSO4溶液被排入水体中。污染源和节点位置如图3所示,具体实验工作可参考前期工作[16]。扩散过程可由式(12)描述[17]: (12) 式中:M是污染物的质量,K为扩散系数,(x0,y0)为污染源位置,t为当前时间。各节点的实地监测数据如表2所示。 图3 实验1中节点部署和污染源位置 数据预处理:显著性水平α=0.05,采用Wilcoxon秩和检验,节点探测时间如表3所示。传感器节点的最小分辨率为0.01 g/L。根据探测时间以及表1中监测数据,节点1,5,3,7在同一圆形浓度等位线上,节点2,4,6,8在同一圆形浓度等位线上。 污染源定位:根据监测数据,不同定位方法的结果如表4所示。表4中,采用了最小二乘方法来求解解析定位问题,使得各节点的浓度监测数据和由式(12)给出的理论浓度值的差值的平方和最小。浓度数据采用的是第20 s的监测数据。粗略定位算法中选取的是第20 s的监测数据的MPA点。基于浓度等位线的质心算法的定位结果是节点1,5,3,7所在圆形等位线以及节点2,4,6,8所在圆形等位线的质心的平均值。从实验1的实验结果来看,质心定位算法有更高的精确度。 表2 实验1中各节点的监测值 表3 节点探测到污染的时间(实验1) 表4 不同定位算法的实验结果(实验1) 实验2:静态水体中受边界限制的浓度场中的污染源定位。 问题背景:在浅滩水体中,位置(x0,y0)=(1.05,6.05)m处有一连续(污染)源,该污染源靠近不透水边界Y。水域大小为10 m×10 m,水深f=10 m。自t0=0 h起污染物溶液被排入水体中,质量流率M为100 kg/h,扩散系数为K=1 m2/h。扩散过程可由式(13)描述[17]: (13) 以λ为变量的erfc函数为: 该实验采用水文仿真软件MODFOLW[18]实现,各节点监测数据如表5所示。在仿真实验中节点(0.85,6.75)和节点(0.85,5.35),节点(0.55,7.25)和节点(0.55,4.85),节点(1.75,7.25)和节点(1.75,4.85),节点(0.15,7.55)和节点(0.15,4.55),节点(2.25,7.95)和节点(2.25,4.15)分别置于同一浓度等位线上。 数据预处理:阈值γ=0.05 g/L。采用简单污染探测算法,各节点探测到污染的时间如表6所示。显然污染源位置的边界条件为B={x0|10>x0>0}。 对比以下3种污染源位置定位方法: 粗略定位方法:在本实验中最大监测点算法(MPA)和最早探测点算法(EPA)得到的为同一点。当节点密集,某节点接近于污染源时,定位精度较高,否则有较大的定位误差。 基于模型的解析定位方法:采用了非线性最小二乘方法来求解解析定位问题,使得各节点的浓度监测数据和由式(13)给出的理论浓度值的差值的平方和最小。浓度数据采用的是第4.0 h的监测数据,定位结果如表7所示。 表5 实验2中各节点的监测值 表6 节点探测到污染的时间(实验2) 本文质心定位方法:不同的节点组合下定位结果不同。例如在节点组1:{(1.35,5.15),(1.35,6.95),(0.85,6.75),(0.85,5.35),(0.55,7.25),(0.55,4.85),(1.75,7.25),(1.75,4.85),(2.25,7.95),(2.25,4.15),(0.15,4.55),(0.15,7.55),节点组2:{(1.35,5.15),(1.35,6.95),(1.75,7.25),(1.75,4.85),(2.25,7.95),(2.25,4.15)},节点组3:{(0.85,6.75),(0.85,5.35),(0.55,7.25),(0.55,4.85),(2.25,7.95),(2.25,4.15)} 下有不同的定位结果,如表8所示。 结合实验结果进行分析,有:①基于扩散模型的水污染源定位算法的结果与数值计算中选择的初值有关,事实上在数值计算中应设置变量边界以使得计算结果收敛。②质心定位算法的定位结果比任何一个监测点离污染源都近。③在本实验中,相对其他污染源定位算法,质心算法有更好的定位结果。 表7 基于模型的解析定位结果(实验2) 表8 不同节点组的定位结果 实验3:一般情形下的质心定位算法 问题背景:在浅滩水体中,水域大小为200 cm×200 cm,水深f=100 cm。在水域中心有一连续(污染)源。自t0=0 s起MgSO4溶液被排入水体中。污染源和节点位置如图4所示。各节点的实地监测数据如表9所示,具体实验工作可参考前期工作[16]。在本实验中,由于溶液排放速率非常量,并没有解析扩散模型,基于模型的解析定位方法无法采用。记节点 1,节点 2,节点 3,节点 4,节点 5,节点 6,节点7,节点 8的位置分别为(a1,b1),(a2,b2),(a3,b3),(a4,b4),(a5,b5),(a6,b6),(a7,b7),(a8,b8)。 表9 实验3中各节点的监测值 表10 节点探测到污染的时间(实验3) 图4 实验3中节点部署和污染源位置 数据预处理:显著性水平α=0.05,采用Wilcoxon秩和检验,节点探测时间如表10所示。传感器节点的最小分辨率为0.01 g/L,根据节点污染探测时间以及监测数据易推得节点3和节点5在同一轴对称浓度等位线上,节点4和节点6在同一轴对称浓度等位线上。 ①一般情形下的定位结果 区域D为: D= 边界条件为B={x0|200>x0>0},基于式(1)的定位结果为(0,140/9)cm。 ②根据浓度等位线的定位结果 根据对称条件,有 定位结果为(0,20)cm。 采用EPA或CPA定位算法时,定位结果是某节点的位置。本实验中得到的估计位置都比各节点离污染源近,即估计结果都优于EPA或CPA定位算法。 纵观以上实验结果,说明了本文水污染源质心算法相对其他典型水污染源定位算法的优越性。 本文提出了一种质心算法定位水污染源。该方法不依赖于扩散模型,其关键步骤是确定污染源所在区域,其次是计算该区域的几何质心,质心位置即污染源位置。当浓度场中存在对称的浓度等位线时讨论了质心算法的解析解。在实验部分检验了本文算法,并与粗略定位算法以及基于模型的解析定位算法进行了对比,实验结果验证了本文算法的有效性。 在后续工作中,将讨论定位算法在实地环境工作中难免遇到的一些问题,如数据有效性问题,即数据使用之前对错误数据的清理;节点漂移问题,即非静态水体中参与污染源定位的观测节点实际位置可能相对于锚位置有所偏差,如何纠正位置漂移带来的估计误差的问题。 [1] Akyildiz I,Su W,Sankarasubramanian Y,et al. A Survey on Sensor Networks[J]. IEEE Communications Magazine,2002,40:102-114. [2] Kamal Z E,Salahuddin M A. Introduction to Wireless Sensor Networks[M]. Driss B D,Al-Fuqaha A. Wireless Sensor and Mobile Ad-Hoc Networks,New York:Springer Press,2015:1-18. [3] Michaelides M P,Panayiotou C G. Plume Source Position Estimation Using Sensor Networks[C]//Proceedings of the 13th Mediterranean Conference on Control and Automation. Limassol,Cyprus:IEEE,2005. 731-736. [4] 匡兴红,邵惠鹤. 无线传感器网络在气体源预估定位中的应用[J]. 华东理工大学学报,2006,32(7):780-783. [5] Wang H,Zhou Y,Yang X L,et al. Plume Source Localizing in Different Distributions and Noise Types Based on WSN[C]//Proceedings of the International Conference on Communications and Mobile Computing,Caen,France:ACM,2010:63-66. [6] Gunatilaka A,Ristic B,Skvortsov A,et al. Parameter Estimation of a Continuous Chemical Plume Source[C]//Proceedings of the 11th International Conference on Information Fusion,Cologne,Germany:IEEE,2008:1-8. [7] Huang C F,Hsing T,Cressie N. Bayesian Source Detection and Parameter Estimation of a Plume Model Based on Sensor Network Measurements[J]. Applied Stochastic Model in Business and Industry,2010,26(4):331-348. [8] Zoumboulakis M,Roussos G. Estimation of Pollutant Emitting Point-Sources Using Resource-Constrained Sensor Network[C]//Proceedings of the 3rd International Conference on Geosensor Networks. Berlin,Germany:Springer,2009:21-30. [9] 罗旭,柴利,杨君. 无线传感器网络下静态水体中的近岸污染源定位[J]. 自动化学报,2014,40(5):849-861. [10] 杨君,柴利,罗旭. 基于无线传感网络的湖库水环境污染源定位方法[C]//第31届中国控制会议论文集. 北京:IEEE,2012:6649-6654. [11] 杨君,罗旭,柴利. 基于无线传感器网络的河流中稳态扩散污染源定位研究[J]. 传感技术学报,2014,27(10):1423-1430. [12] Zhao T,Nehorai A. Distributed Sequential Bayesian Estimation of a Diffusive Source in Wireless Sensor Networks[J]. IEEE Transactions on Signal Processing,2008,55(4):2213-2225. [13] Qing Y,Lim A,Casey K,et al. Real-Time Target Tracking with CPA Algorithm in Wireless Sensor Networks[C]//Proceedings of the 5th Annual IEEE Communications Society Conference on Sensor,Mesh and Ad Hoc Communications and Networks,San Francisco,USA:IEEE,2008:305-313. [14] Yang J,Luo X. A Study on Water Pollution Source Localization in Sensor Networks[J/OL]. Journal of Sensors,2016,http://dx.doi.org/10.1155/2016/9528050. [15] Walpole R E,Myers R H,Myers S L,et al. Probability and Statistics for Engineering and Scientists,8th ed[M]. New Jersey,America:Pearson Prentice Hall,2007. [16] 杨君. 基于无线传感器网络的水环境污染源探测与定位[D]. 武汉:武汉科技大学,2016. [17] 彭泽洲,杨天行,梁秀娟. 水环境数学模型及其应用[M]. 北京:化学工业出版社,2007:24-33. [18] Aquaveo. GMS manual[OL]. http://xmswiki.com/wiki/GMS:GMS_User_Manual9.2,2016-05-13.
2 定位方法
2.1 解析特解

(x2-x0)2+(y2-y0)2=r2
(x3-x0)2+(y3-y0)2=r2
⋮
(xI-x0)2+(yI-y0)2=r2

2.2 数据预处理

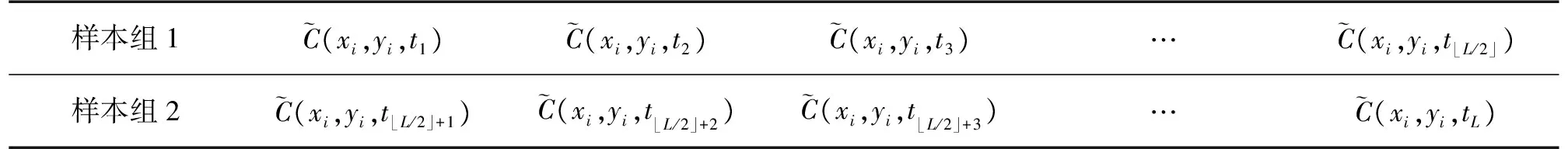
2.3 算法适用性
3 实验


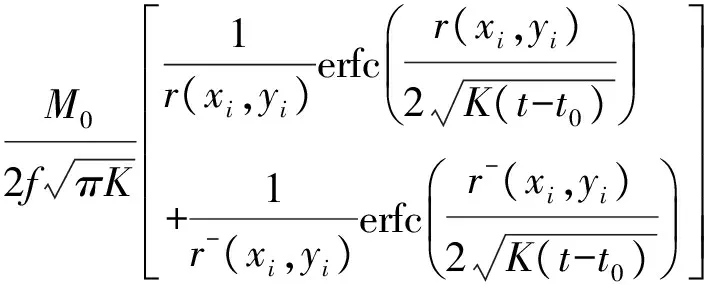






5 结论和未来研究工作
