混沌优化细菌觅食算法的传感器节点部署策略*
2018-02-05王振东陈峨霖胡中栋
王振东,陈峨霖,胡中栋
(江西理工大学信息工程学院,江西 赣州 341000)
广泛应用于地质监测、环境保护等领域的自组织多跳无线传感器网络WSN(Wireless Sensor Network)具有部署灵活、成本低廉、覆盖范围广等优点[1],但监测区域的大范围随机部署会带来节点分布不均匀问题[2],针对该问题,众多学者运用群智能仿生算法进行优化处理[3]。文献[4]基于人工鱼群算法构建网络覆盖模型,通过模型求解来优化网络覆盖。文献[5]利用概率感知模型将遗传算法与粒子群算法相结合来优化网络覆盖。文献[6]提出使用有效质心和重叠质心改进虚拟力计算公式和节点往复运动优化网络节点部署。为了克服粒子群算法容易陷入局部最优等,后期收敛速度慢等缺点,文献[7]采用混沌运动对原始算法进行了优化。文献[8]提出一种在不同网络规模及连通度都可以明显提高传感器网络的节点定位准确度及网络覆盖率的算法。文献[9]采用改进蚁群算法的方式优化离散监测区域的网络覆盖率。上述群智能算法在WSN覆盖优化问题上取得了较大成效,但也存在诸如求解复杂度高、收敛速度慢、收敛精度低、运算成本大等问题。
对此,本文提出一种混沌优化的细菌觅食算法COBFA(Chaos Optimization of Bacterial Foraging Algorithm),并基于该算法对监测区域节点部署情况进行仿真。研究表明,现有细菌觅食算法对全局空间寻优能力差,搜索速度和搜索精确度均有待提高,且容易陷入局部最优及产生早熟。针对上述问题,首先构造菌群密度函数因子、细菌反弹因子及自适应细菌趋化步长来改进细菌觅食过程中的翻转概率和细菌的趋化步长。然后,依据混沌系统的遍历性,随机生成混沌扰动序列来帮助细菌翻转后对方向的选择,当菌群繁殖时利用交叉和变异操作以避免细菌搜索到局部最优。最后,利用自适应菌群迁徙概率来提高算法的收敛速度,使最终部署的WSN网络具有较高的综合覆盖率及较低的能量消耗。
1 相关模型
本节主要介绍需要用到的基本模型和基本算法。主要包括:节点之间的距离模型,节点能量消耗计算公式,如何计算节点覆盖面积并构造联合覆盖率目标函数,接着介绍基本BFO算法。算法主要工作是求解构造的目标函数。
1.1 节点距离模型
随机抛撒在监测区域的大量传感器节点可以视为随机且相互独立[10]。设定单个节点的感知半径为r,通讯半径为R,在应用中R≥2r。o(i)是位于目标监测区域内的一个传感器节点[11],其坐标的位置为(xi,yi),(xj,yj)是另一个位于目标监测区域内的某个传感器节点g(j)的坐标。则节点o(i)到节点g(j)的距离为:
(1)
1.2 能耗模型
WSN节点消耗的能量包括收发数据、处理数据和其他能量消耗,能耗模型使用文献[12]中的模型,本文主要考虑收发数据消耗的能量。则节点在相距为d*m时发送l*bit的数据消耗的能量为:
(2)
ER(l*)表示节点接收l*bit数据消耗的能量:
ER(l)=lEelec
(3)
则节点剩余能量为:
Es=E0-q*Emem-p*ET(l*)
(4)

1.3 节点探测概率
本文采用奈曼—皮尔逊准则[13]的感知模型计算传感器的探测概率,设传感器节点存在高斯噪声并对其进行相互独立的处理,那么第a个目标点的测量值为:
(5)
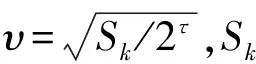
则接收信号ra在H0和H1情况下的概率密度函数分别为:
(6)
(7)
式中:σ是噪声的标准差,由奈曼—皮尔逊准则:
准则:
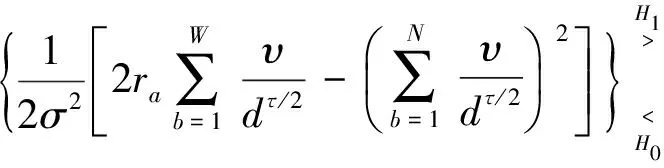
(8)
式中:ω为阈值,由式(5)得:
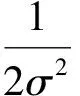
(9)
由式(6)可得:
(10)
那么得到的WSN节点误警率是:
(11)
则节点b对目标点a的探测概率为:
(12)
式中:W为可以探测到目标a的周围固定节点的个数。
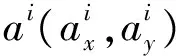
(13)
那么WSN的有效覆盖率为:
(14)
定义1联合覆盖目标函数 WSNs联合覆盖是指在保证能量均衡的情况下利用较少节点达到较大的网络覆盖率,综合考虑WSN工作节点数、有效覆盖率和剩余能量均衡性的联合覆盖目标函数f为:
f=w1f1+w2f2+w3f3
(15)
式中:w1、w2、w3为权值,且;
w1+w2+w3=1
(16)
式中:f1为WSN有效覆盖率,f2为WSN节点闲置率:
f2=(N-N′)/N
(17)
N为WSN节点的部署总数,N′为WSN工作的节点数,节点闲置率越大越好。
WSN剩余能量均衡函数为f3,表示WSN局部区域的剩余能量均衡程度,其值越大,局部区域内的节点生存时间越长。
(18)
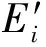
将目标函数转化为多目标优化过程来求f得极大值,即求子函数:f1、f2、f3的极大值及其对应权重系数。
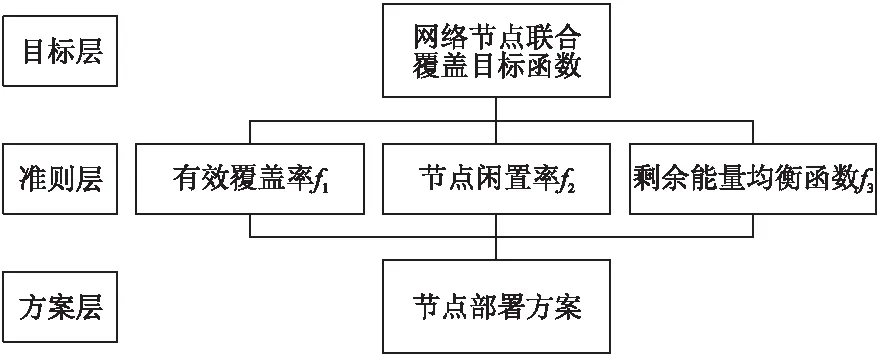
图1 AHP层次结构模型
1.4 AHP确定权值系数
在多因素或多目标决策过程中,层次分析法[14]AHP(Analytic Hierarchy Process)应用相对广泛,主要包括6个步骤:构造阶梯层次结构、建立判断矩阵、判断矩阵一致性检验、层次单排序和总排序和对分析结果进行决策。本文采AHP对f中的权值系数w1、w2、w3优化求解。
根据式(15)中f1、f2、f3与节点部署之间的关系建立层次结构模型如图1所示。
从图1目标层开始,自上而下依据上一层元素分别同下一层元素中与之关联的元素两两比较,建立判断矩阵A。
由实验得出的准则层因素相对比重如判断矩阵A:

经过一致性检验可知矩阵A具有近似一致性。权值向量由计算A的最大特征根及其对应特征向量可得:
w=[0.633 3 0.106 2 0.260 5]T
在双层层次结构模型中,单排序权重w与总排序权重相同,所以由w得到的三因素权值系数为:
w1=0.633 3,w2=0.106 2,w3=0.260 5
1.5 基本BFO
BFO(Bacterial Foraging Optimization Algorithm)是一种受细菌觅食行为启发提出的仿生群智能算法[15],设置3种算子代表细菌在觅食过程中的趋化、繁殖和迁徙行为来寻找种群最优。
定义2趋化算子
菌群趋化算子表示单个细菌在寻找食物时以一定概率向任意方向翻转,并在该方向以单元步长游动:
θi(g+1,s,l)=θi(g,s,l)+c(i)×φ(i)
(19)
(20)
式中:θi(g+1,s,l)表示单个细菌粒子进行g次趋化、s次移动和l次繁殖操作时细菌i的位置函数,c(i)是细菌游动的趋化步长,Δ(i)为细菌变向过程中生成的某个方向向量,φ(i)为细菌调整方向后的单元步长向量。
定义3繁殖算子
对于搜索菌群,细菌趋化循环后选择性繁殖,通过对细菌适应度排序,淘汰一半较差适应度的细菌后分裂复制另一半细菌保持细菌总数不变。假设第i个细菌适应度累加和为:
(21)
J(i,g,s,l)代表细菌i在l次迁徙、s次复制、g次趋化时的适应度。
定义4迁徙算子
对于搜索菌群,趋化繁殖若干次后,细菌个体随机分布在监测区域,假设以概率Ped对菌群进行驱散操作来避免觅食过程过早收敛,提高全局搜索最优解的概率。
1.6 基本BFO步骤
Step 1 随机初始化N个细菌,细菌的趋化、复制、迁徙次数分别为Nc,Nre,Ned。操作计数参数设为g,s,l,θi(g,s,l)表示细菌第g次趋化,第s次复制,第l次迁徙的位置。单个细菌的趋化步长为c(i),在相同方向最大趋化步数为Nc,迁徙概率为Ped,细菌搜索维度为d。
Step 2 计算细菌的初始适应值J(i,g,s,l)。
Step 3 趋化行为g=g+1。
Step 4 复制行为s=s+1。
Step 5 迁徙行为l=l+1,
对细菌i=1,2,…,N,按如下方法进行趋化循环操作。
(1)用Jlast=J(i,g,s,l)存储当前最佳适应度值。
①翻转,产生随机向量Δ(i)∈Rn,且Δm(i),(m=1,2,…,N)随机分布在[-1,1]。
②移动,
θi(g+1,s,l)=θi(g,s,l)+c(i)×φ(i),
其中c(i)表示细菌i翻转后游动的步长。
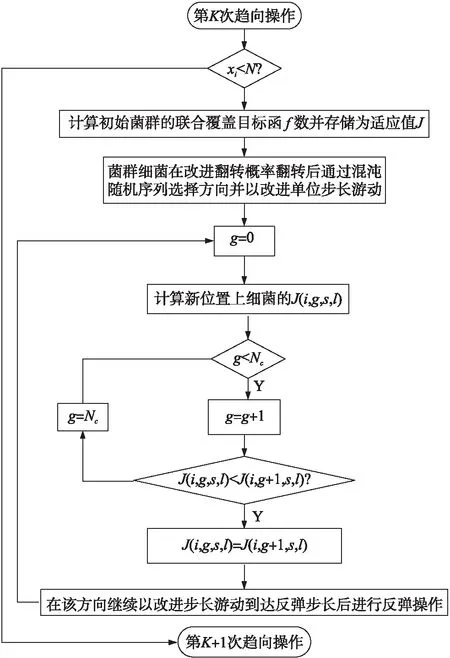
(2)用θi(g+1,s,l)计算适应度值J(i,g+1,s,l),用g计数细菌游动次数,让g=g+1.若J(i,g+1,s,l) 若g Step 7 若s Step 8 按给定概率Ped对每个细菌i=1,2,…,N进行迁徙行为,让Ped小于随机值的细菌存活并分布于寻优空间,若l 本节主要介绍构造的联合覆盖率目标函数模型如何求解;为了避免细菌的位置难以与WSN节点位置重合,首先定义了细菌粒子与节点的编码映射,然后通过对Logistic映射方程初值及参数的对比实验,寻找能迭代出的具有较好遍历性和全局搜索能力的混沌随机序列的初值及参数,帮助细菌在趋化行为阶段细菌翻转后选择方向。 改进BFO包括:细菌在趋化阶段进行行为翻转时,改进趋化翻转概率,引入时间参数因子对翻转概率进行动态调整来保证算法的精确性;细菌翻转后,用混沌模型生成的混沌随机序列帮助细菌选择方向;在移动行为时,设置菌群密度函数因子,以适应细菌周围环境的影响。此外,对细菌的趋化步长进行动态调整,当细菌之间的距离小于阈值时,利用反弹步长使细菌向食物感知系数大的方向移动;在细菌繁殖阶段,使用交叉算子和变异算子改善细菌的适应度,并计算各个菌群的联合覆盖率以求解联合覆盖率目标函数模型;最后在迁徙阶段动态调整迁徙概率以确保细菌具有较好的寻优能力。 针对构造的联合覆盖目标函数多目标优化模型(15)采取如图2所示的方法求解。 图2 多目标优化模型求解流程图 定义5编码映射关系: 假设菌群对监测区域离散搜索时细菌粒子与WSN节点位置间的相互映射[16]函数为: Z(Xid)={Xnd|min(‖Xnd-Xid‖)}1≤n≤N (22) 式中:Xnd表示WSN的节点位置,Xid表示细菌粒子的位置,‖Xnd-Xid‖是欧氏距离,d是离散搜索的空间维度(本文中d=2)。 菌群为监测目标区域的节点集合,一个菌落由e个细菌粒子构成,代表一种节点部署方案。每个粒子代表一个WSN节点,细菌的搜索维度为2,表示二维搜索平面x轴和y轴的取值,区域内节点的联合覆盖率代表细菌的适应度值。 混沌优化CO(Chaos Optimization)依据混沌运动对初始值敏感性且能按照自身搜索规律在搜索范围内不重复遍历搜索所有状态来提高搜索效率[17]。 著名的Logistic混沌映射方程表达式为: zn+1=cρ(ρ,zn)=ρxn(1-zn),zn∈(0,1) (23) 式中:ρ表示混沌映射系统的参数。若zi=[mi,ni],那么可由式(24)、式(25)对混沌序列[14]zi进行往返映射。 (24) (25) Logistic映射系统十分敏感初值和参数,不同的初值和参数可能得到不同的混沌随机序列,通过研究混沌运动的轨迹所生成的轨迹序列分布图直观表示,在细菌觅食时加入混沌随机序列,提高了菌群的多样性和全局寻优能力。 图3表示不同初值z0,参数ρ通过Logistic方程迭代500次后得到分布在(0,1)区间上的轨迹序列分布图,利用它来寻找具有较好遍历性和全局搜索能力的混沌随机序列。 图3 5种初值和参数的时轨迹序列分布图 由图3知当初值z0=0.6576,参数ρ=2.5、z0=0.997 8,参数ρ=3.56和z0=0.5,参数ρ=4时,Logistic混沌映射方程迭代生成的的生成的随机序列分布不均匀,在(0,1)区间上形成的是近似于直线的间断运动轨迹没有较好的均匀性和遍历性。当初值z0=0.997 8,参数ρ=3.8时,Logistic混沌映射方程迭代产生的混沌序列随机分布于(0,1)区间,但该初值和参数生成的混沌序列分布在一个带状区域,序列并不能对搜索区域完全遍历相关区域。当初值z0=0.997 8,参数ρ=4时,Logistic混沌映射方程通过迭代可以在(0,1)区间上形成分布较为平均的且有着很好遍历性的混沌随机序列,该序列能够对搜索区域进行全局搜索。所以在后文利用Logistic混沌映射方程迭代产生混沌随机序列时选取的是初值z0=0.997 8,参数ρ=4。 2.4.1 菌群密度函数 单个细菌不断感知菌群拥挤程度以减小菌群周围环境影响搜索结果,根据细菌间的平均距离动态调整搜索细菌的趋化步长。设菌群密度函数因子为: (26) 感知细菌密度改进趋化函数: C(i)=A×D(k)+B (27) 式中:Cmin与Cmax,Dmin与Dmax分别是细菌最小、最大趋化步长,最小、最大间隔距离。 Cmin≤C(k)≤Cmax,Dmin≤D(k)≤Dmax, A=(Cmax-Cmin)/(Dmax-Dmin), B=(DminCmax-DmaxCmin)/(Dmax-Dmin)。 2.4.2 趋化反弹步长 细菌趋化阶段加入反弹系数,当菌落内细菌i和j距离小于设定阈值,细菌i对细菌j产生反弹作用,使其各自向食物感知系数大的方向迁徙,sij表示细菌i和j反弹后的游动距离,α表示节点的冗余覆盖度: (28) 2.4.3 冗余覆盖度 节点i的冗余覆盖度[18]表示i感知区域内邻居节点nei(i)感知面积与节点感知面积的重叠区域与节点感知面积的比值,用式(29)计算: (29) 式中:axi代表节点i的感知面积区域。 axi= (30) 式中:n为i的邻居节点数目,r为节点感知的半径,dit为邻居节点t与节点i的距离。 2.4.4 趋化翻转概率 在细菌觅食时引入时变衰减函数作为衰减因子β,改进觅食时细菌的翻转概率[19],通过时间参数因子对翻转概率进行动态调整来保证算法的精确性。其函数为: visk+1=β×visk+vismin (31) β=e-Ti-T0 (32) 式中:T0表示算法初始运行时间,Ti表示算法当前运行时间,vismin为给定的最小翻转概率,开始时β值较大,函数快速收敛且翻转概率大。随着时间的推移,β逐渐变小,翻转概率也会慢慢变小最终达到最小值。 2.4.5 繁殖算子改进 细菌繁殖阶段利用交叉算子使健康细菌在搜索过程中起正向作用以改善适应度差的细菌个体,适应度差的半数细菌个体与适应度好的健康细菌先相互杂交;同时为了防止菌群早熟陷入局部最优解,设置菌群变异算子对杂交后的高适应度的半数细菌进行随机微小扰动后复制分裂。 菌群细菌的交叉算子设为: F″(i)=χX(i)+(1-χ)X(best),i=1,2,…,N (33) 式中:χ为[0,1]均匀的随机数,X(best)为菌群搜索的高适应度细菌的编号,F″(i)为高适应度细菌的坐标信息。 菌群细菌的变异算子设为: F′(i)=F(i)+Y,i=1,2,…,N (34) 式中:Y服从标准正态分布N(0,1)。 2.4.6 动态迁徙概率调整 细菌迁徙阶段以概率Pself对迁徙概率动态调整: (35) 式中:Jnum是适应度函数,Ped是原始迁徙概率。 Step 1 随机初始化N个细菌,细菌的趋化、复制、迁徙次数分别为Nc,Nre,Ned.设3种操作循环计数参数为g,s,l,θi(g,s,l)表示细菌第g次趋化,第s次复制,第l次迁徙的位置.单个细菌的趋化步长为c(i),在相同方向最大趋化步数为Nc,迁徙概率为Ped,细菌搜索维度为d。 Step 2 计算初始化细菌的f作为适应度值J(i,g,s,l)。 Step 3 趋化行为g=g+1。 Step 4 复制行为s=s+1。 Step 5 迁徙行为l=l+1, 对细菌i=1,2,…,N,按如下方法进行趋化循环操作。 (1)用Jlast=J(i,g,s,l)存储当前适应度值。 ①翻转;根据式(31)计算在细菌在趋化行为时的趋化翻转概率。 ②移动; Ⅰ.产生混沌随机序列.依据混沌系统的遍历性,随机生成混沌随机序列帮助细菌翻转后对方向的选择, 由式(23)选择初值z0=0.997 8,参数ρ=4后由混沌系统迭代出确定的混沌随机序列z1,z2,z3,…。 zxi+1=ρzxi(1-zxi),i∈(0,1) (36) 式中:ρ为混沌控制参数。 (a)搜索细菌xi的Pbestxi通过式(37)映射到式(36)Logistic方程定义域(0,1)上。 zxi=(Pbestxi-axi)/(bxi-axi) (37) 式中:axi,bxi为节点坐标范围。 (b)通过Logistic方程zxi+1=ρzxi(1-zxi)多次迭代得到混沌序列: zm(m=1,2,3,…) (38) (c)把产生的混沌序列通过式(25)逆映射 (39) 从而返回原解空间并产生一个含有混沌变量的可解混沌序列: (40) 菌群中的细菌按此序列对搜索空间寻优。 Ⅱ.混沌游动方向序列: 及游动步长 θi(g+1,s,l)=θi(g,s,l)+C(i)×φ(i) 来使细菌游动以寻找最优适应度值。其中c(i)表示细菌i翻转后游动的步长,且当菌落内细菌i和j距离小于设定阈值,细菌i对细菌j产生反弹作用,使其各自向食物感知系数大的方向迁徙,sij表示细菌i和j反弹后的游动距离。 (2)用θi(g+1,s,l)计算适应度值J(i,g+1,s,l),用g计数细菌游动次数,让g=g+1.若J(i,g+1,s,l) 若g 图4 Step 6 对细菌i=1,2,…,N,进行Nc次趋化行为后; ②对适应度值较差的半数细菌用交叉算子与挑选出的精英细菌进行杂交,生成N/2个新细菌,然后用变异算子F′(i)=F(i)+Y,i=1,2,…,N对交叉操作后的一半细菌进行变异操作后复制分裂构成新细菌群Nnew。 Step 7 若s Step 8 按式(35)计算概率并对每个细菌i=1,2,…,N进行迁徙行为,让Pself小于随机值的细菌存活并重新分布于寻优空间,若l 在MATLAB2010b环境下使用经典的LEACH协议仿真算法,(协议运行步骤为:选取簇头并形成簇、 建立时隙表和稳定运行。)800 m×800 m矩形区域平面随机分布200个传感器节点。每个节点代表菌群中的一个细菌,节点的监测半径r=50,通信距离R=100,初始化算法的各项参数,Nre∶Nc∶Ned=5∶60∶3初始节点能量E0=0.5 J,趋化步长c是0.05,反弹碰壁系数α为0.05,迁徙概率为0.25,单方向翻转最大次数为15次,实验结果如图所示。图4(a)、图4(b)为随机分布节点对监测区域进行覆盖时节点的部署情况及覆盖率曲线图,图4(c)为用BFO优化后得到的WSN部署节点情况,图4(e)为用COBFA算法优化后得到的WSN部署节点情况,其中黑点和圆分别表示传感器节点坐标位置信息和节点覆盖面积区域。 分析图4~图6可知,随机节点部署策略中节点在区域分布极不均匀,出现覆盖空洞的同时也存在有大量的节点冗余和大面积重复覆盖,节点覆盖率为91.15%,经过细菌觅食算法优化节点部署休眠冗余覆盖度大的节点后节点覆盖比较均匀,减少了重复覆盖区域,但仍然存在较多的冗余节点和覆盖空洞,其覆盖率为96.71%。在用混沌优化的细菌觅食算法得到的节点覆盖方案中WSN节点在监测区域中均匀分布,休眠冗余覆盖度大的节点后,几乎不产生节点冗余,并且覆盖率能够到98.97%,几乎没有覆盖空洞。与随机部署节点的策略比较,通过混沌序列优化细菌觅食算法得到节点部署策略网络覆盖率提高了7.82%,节点在监测区域分布更加均匀,重复覆盖的区域更少,节点的冗余度极低,达到了WSN优化覆盖的目的,而且优化的算法使用更少的节点就能有效覆盖监测区域,节约了部署成本,同时也极大地延长了WSN的监测时间。 由表1可知,混沌优化过的细菌觅食节点部署策略其网络平均覆盖率高于其他对比算法,且使用的节点个数少于其他节点部署算法,节点的利用率、能量平衡性优于其他节点部署算法且搜索最优覆盖策略的速度最快,通过互相对比发现,COBFO优化算法能够有效提高节点的利用率、网络覆盖率、降低节点能量消耗及延长网络生存寿命。 图5 生存周期对比曲线 图6 节点剩余能量对比曲线 表1 部署策略比较 本文针对监测区域节点随机部署时网络存在冗余覆盖面积大、能量不均匀消耗及细菌觅食未优化算法存在的易陷入区域局部最优、后期搜索速率慢等缺陷,用混沌理论对原始细菌觅食算法改进后优化WSN覆盖。仿真表明,改进的节点部署策略与节点随机部署覆盖策略及未优化的细菌觅食算法部署策略比较,通过改进算法得到的WSN节点部署策略有着较高网络覆盖率及节点综合利用率,增加算法的搜索能力和探索速度,有效地增强搜索的精确性,能够实现优化节点覆盖、节约节点能量、提高WSN覆盖率,大幅降低节点重复覆盖面积及节点冗余度,提高WSN的监测时间。 [1] Singh M,Khilar P M. A Range Free Geometric Technique for Localization of Wireless Sensor Network(WSN)Based on Controlled Communication Range[J]. Wireless Personal Communications,2016:1-27. [2] 牛玉刚,杜国杰,贾廷纲. 一种基于能耗均衡的分区节点部署算法[J]. 控制与决策,2016,31(6):1021-1026. [3] 张梦蓓,乔帅. WSN中节点分布的协方差矩阵自适应优化策略[J]. 仪表技术与传感器,2016(2):83-86. [4] 范政武,王铁,陈峙. 基于人工鱼群算法的车辆平顺性优化分析[J]. 农业工程学报,2016,32(6):107-114. [5] 丁旭,吴晓蓓,黄成. 基于改进粒子群算法和特征点集的无线传感器网络覆盖问题研究[J]. 电子学报,2016,44(4):967-973. [6] 黄帅,程良伦. 一种基于虚拟力的有向传感器网络低冗余覆盖增强算法[J]. 传感技术学报,2011,24(3):418-422. [7] Kwon O M,Park M J,Ju H P,et al. Script H∞Synchronization of Chaotic Neural Networks with Time-Varying Delays[J]. Chinese Physics B,2013,46(11):244-252. [8] 陈跹. 无线传感器网络节点自定位算法研究[D]. 重庆:重庆大学,2014. [9] 马学森,曹政,韩江洪,等. 改进蚁群算法的无线传感器网络路由优化与路径恢复算法[J]. 电子测量与仪器学报,2015,29(9):1320-1327. [10] 王成成. 基于蒙特卡洛方法的移动无线传感器网络节点定位技术研究[D]. 山东大学,2014. [11] 赵玫,杨洪勇,李路伟. 基于权重的目标覆盖控制算法[J]. 控制与决策,2014(10):1845-1850. [12] 张品,王佳佳,占梦. 能量高效的无线传感器网络非均匀分簇路由算法[J]. 传感技术学报,2016,29(12):1919-1923. [13] 胡楠,吴成东,于晓升,等. 基于C-V模型的网络覆盖空洞探测与修复算法[J]. 控制与决策,2016,31(8):1424-1428. [14] 于春娣,丁勇,李伟,等. 一种能量有效的WSN目标跟踪动态协同自组织算法[J]. 传感技术学报,2012,25(11):1577-1583. [15] 姜建国,周佳薇,周润生,等. 一种采用改进细菌觅食优化算法的图像增强方法[J]. 控制与决策,2015(3):461-466. [16] Zhang Z,Li J X,Liu L. Distributed State Estimation and Data Fusion in Wireless Sensor Networks Using Multi-Level Quantized Innovation[J]. Science China Information Sciences,2016,59(2):1-15. [17] 王伟,朱娟娟,万家山,等. 基于混沌量子粒子群算法的无线传感器网络覆盖优化[J]. 传感技术学报,2016,29(2):290-296. [18] 周文宏,雷欣,姜建国,等. 变概率混合细菌觅食优化算法[J]. 系统工程与电子技术,2016,38(4):960-964. [19] 蒋鹏,王兴民. 网络分层的水下传感器网络覆盖保持路由算法[J]. 电子学报,2016,44(5):1240-1246.
2 模型求解
2.1 多目标优化模型求解
2.2 混沌模型
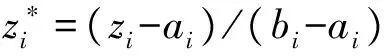
2.3 初值及参数影响产生的混沌序列
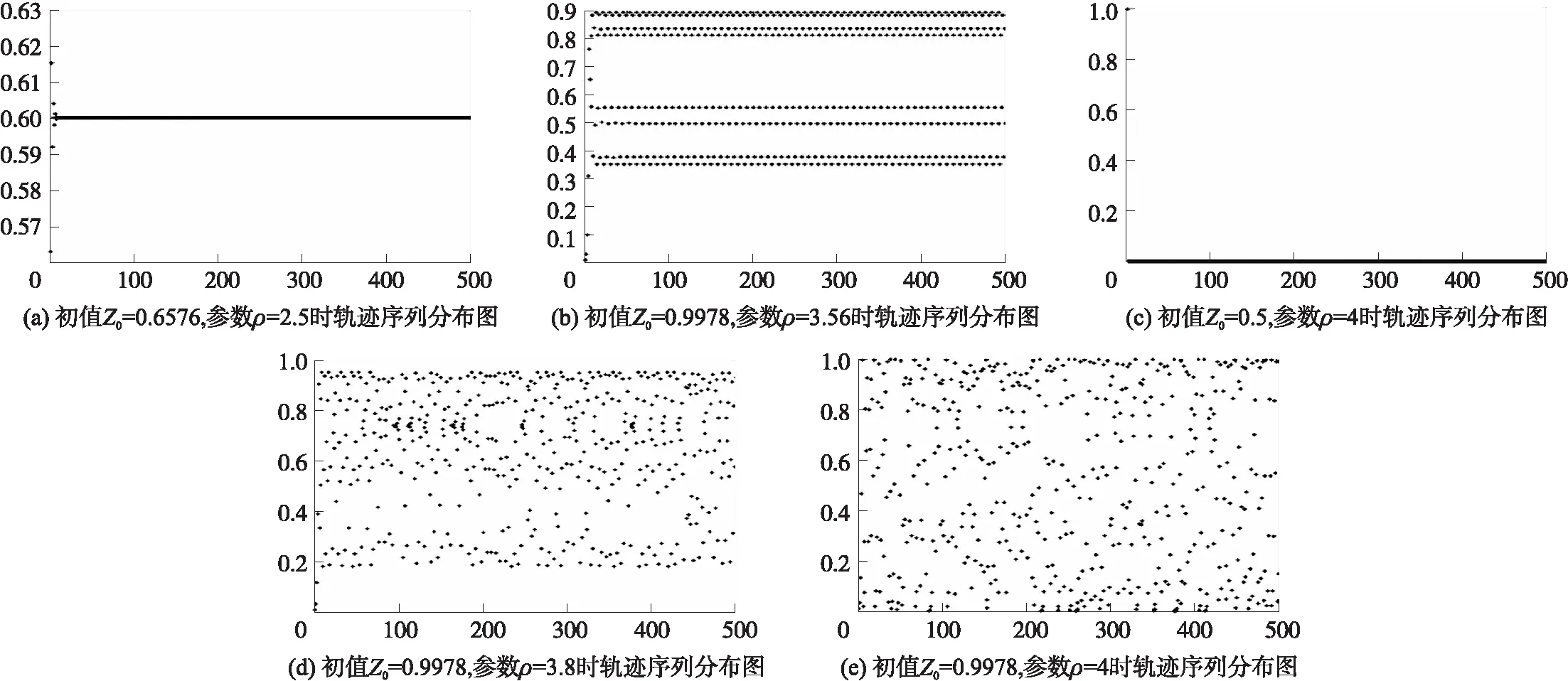
2.4 细菌觅食算法改进
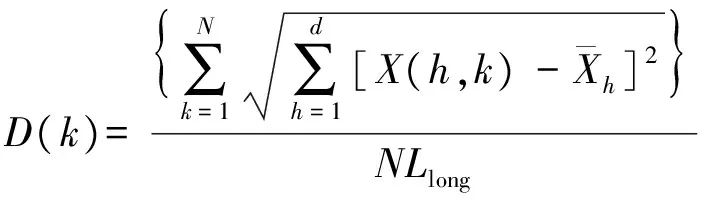

3 算法及分析
3.1 步骤
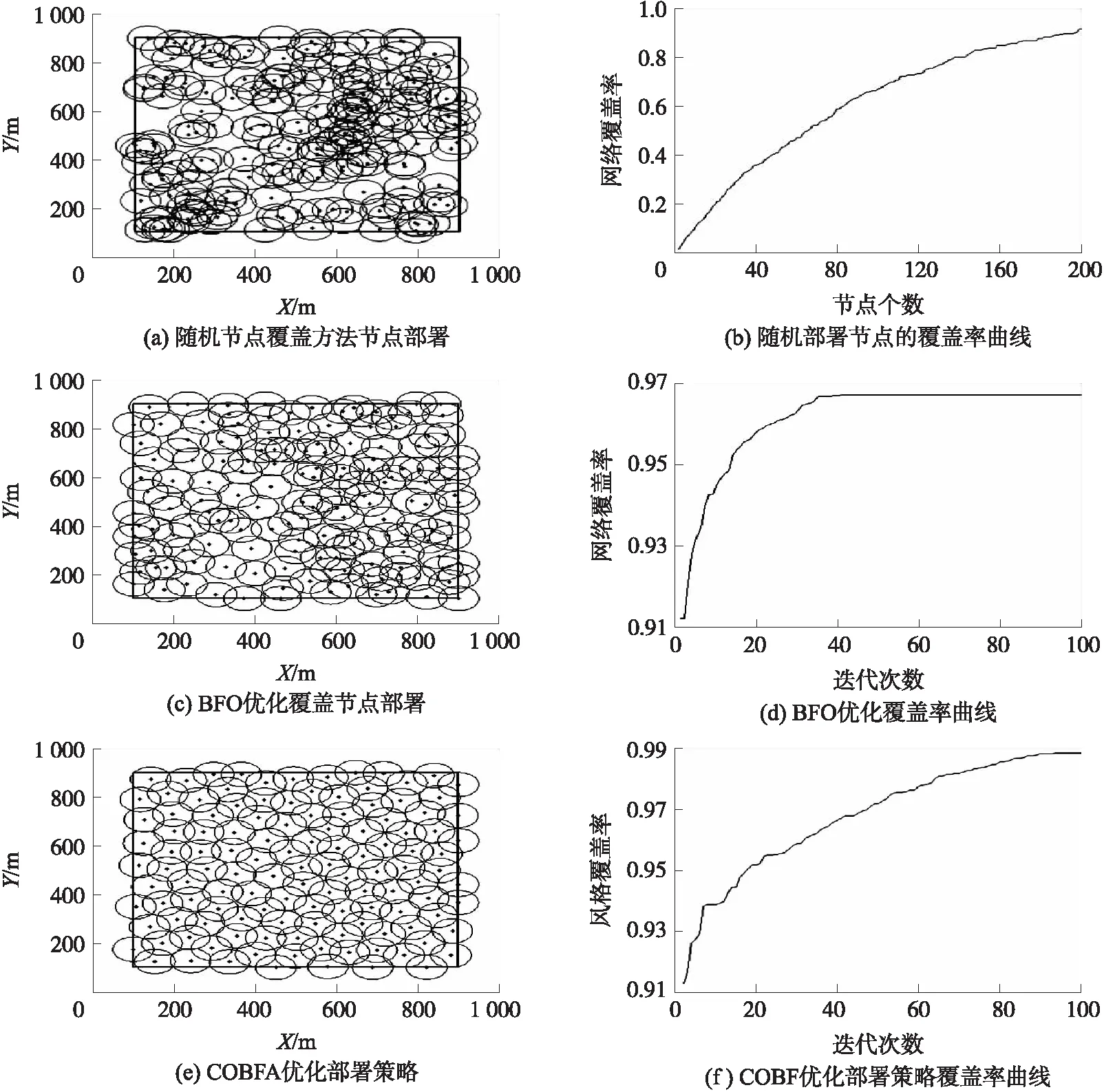
3.2 实验分析



4 结束语
