面向皮纳卫星姿态确定的MEMS陀螺磁强计组合滤波系统*

杜超禹,蒙 涛,金仲和

(1.浙江大学信息与电子工程学院,杭州 310027;2.浙江大学航空航天学院,杭州 310027)

皮纳卫星因功耗、体积约束,其姿态确定系统主要使用MEMS陀螺、磁强计、太阳敏感器[1]。当卫星处于阴影区或任何太阳敏感器不可用状态下时,陀螺与磁强计的组合就显得格外重要,该组合也是皮纳卫星低功耗、全轨、全天时姿态解算的最小系统。

目前微小型化的磁强计可以达到100 nT甚至更高的敏感精度;而MEMS陀螺随机漂移较大,并需要对零偏漂移校准,使得其精度受限[1-2],是该敏感器组合姿态确定精度不高的主要原因。

MEMS陀螺仪的随机漂移误差主要由确定性漂移和非确定性随机漂移组成。确定性误差作为系统误差,可以通过标定等环节加以消除[3],而随机误差没有明显的统计规律,是其精度提升工作的重点。文献[3-7]通过时间序列分析对MEMS陀螺进行误差建模并进行软件算法修正,但并没有考虑陀螺零偏变化对建模的影响,不适用于其长期工作的实时补偿;文献[2]基于Allan方差分析对陀螺零位误差的综合评定,提出了一种动态的零值偏移误差补偿算法;文献[8]通过对原始数据序列求均值的方法去除陀螺常值零偏的影响;文献[9]基于集合经验模态分解和支持向量机的混合建模方法,实现对陀螺漂移序列的区间预测;文献[10]针对大温差应用环境,提出了一种无需分段、全温度区间线性回归补偿模型,对陀螺零偏进行补偿。文献[11]从工程角度设计了适用于星载应用的MEMS陀螺与磁强计组合定姿算法;文献[12]基于光纤陀螺与磁强计设计了改进平方根sigma点卡尔曼滤波器,但工作中使用的陀螺精度都较高。上述研究或仅针对陀螺本身的随机噪声,或仅针对陀螺的零偏补偿,或陀螺精度高重点放在工程简化与算法提升,未提出皮纳卫星中低精度陀螺的在轨数据处理,并应用于卫星姿态确定的实用方案。

本文基于MEMS陀螺与磁强计的适用于皮纳卫星的低功耗、全轨、全天时最小姿态敏感组合,提出一种适用于在轨运行的滤波系统方案。该方案通过在线滑窗ARMA建模降低陀螺随机噪声的影响,由姿态滤波器估计所得的陀螺零偏,并在线去除其常值分量,以保证建模的长期有效性。该系统方案有效降低了陀螺随机噪声,获得了更精确的陀螺零偏估计,提高了该最小敏感器组合的在轨姿态确定精度。

1 在轨滤波系统设计

为了提高该组合的姿态确定精度,本文在轨滤波系统主要完成如下功能:MEMS陀螺ARMA滑窗建模、随机噪声滤波,姿态信息、陀螺零点估计,以及陀螺零偏反馈补偿。具体说明如下:①陀螺ARMA滑窗建模。陀螺通过时间序列ARMA分析,在线建立其在轨数学模型。该在线滑窗建模基于陀螺历史及最新采样信息,并定时更新;②陀螺随机噪声滤波。将①中所得陀螺在轨模型接入随机噪声滤波器,降低原始采样数据的噪声干扰;③陀螺零点、姿态信息估计。降噪后的陀螺数据与磁强计共同接入陀螺零偏及姿态估计器。该估计器分两个阶段:入轨阶段仅使用陀螺数据,通过姿态动力学模型快速得到陀螺零偏的粗估计;待陀螺、磁强计共同接入的姿态估计器收敛后,得到卫星姿态信息以及陀螺零偏的精估计;④陀螺零偏反馈补偿。③中所得陀螺零偏的粗/精估计,作为补偿值反馈接入①中的ARMA分析,以进一步提高在线建模的精度。

该最小姿态确定在轨滤波系统框图如图1所示。

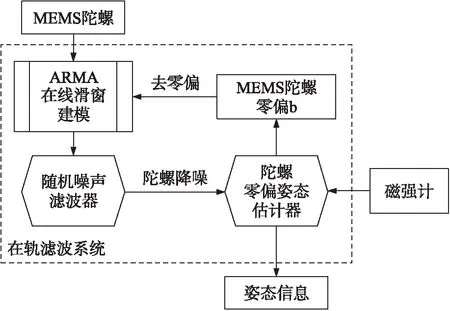
图1 本文基于MEMS陀螺、磁强计的在轨组合滤波系统框图

2 MEMS陀螺随机噪声建模与处理

2.1 模型建立与选择

工程上,时间序列建模法展现了其对随机序列以及实际物理系统统计特性的强大分析能力[4,13-14]。本文对MEMS陀螺随机漂移序列建立若干个时间序列分析模型,并根据工程上常用的AIC信息准则选择确定适用模型[15],该准则简化公式为

(1)

式中:n为序列数据个数。文献[7,15]对数据样本进行了自相关系数、偏自相关系数分析,但该相关特征不明显,在此不做主要考虑。陀螺漂移模型的阶次都较低,一般不超过2到3阶[8],本文分别建立AR(1)、AR(2)、AR(3)、ARMA(1,2)、ARMA(2,1)模型,计算每个模型的AIC值,并取AIC值最小的模型作为适用模型,并确定模型阶次。两种时间序列建模方法如下[4]:

①自回归AR(p)模型

yt=φ1yt-1+…+φpyt-p+εt

(2)

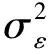
②自回归滑动平均ARMA(p,q)模型

yt=φ1yt-1+…+φpyt-p+θ1εt-1+…+θqεt-q+εt

(3)

当q=0时,该模型退化为p阶AR模型;当p=0时,该模型退化为q阶MA模型。

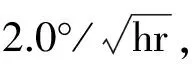
其中较优的为AR(1)以及ARMA(2,1)模型。文献[4-6,8]皆因计算复杂性选择了前者;考虑皮星二号及后续卫星平台的DSP处理器能力强,在此选取模型复杂但精度更高的ARMA(2,1)模型进行后续分析。

表1 各时间序列模型AIC准则对比结果

2.2 适用于在轨姿态确定的建模在线滑窗设计

MEMS陀螺随机误差数据为有序的非平稳随机过程信号,可按照统计理论处理数据输出,建立能够反映系统状态的数学模型[3,8]。本文考虑一种基于陀螺历史及最新信息的在线滑窗ARMA建模,设置滑窗时间区间τ。待建模及处理数据由历史1/2τ数据与最新1/2τ数据拼接而成,如式(4)所示:

(4)

考虑中央处理器存储空间及运算或读取实时性,建模在线滑窗时间区间τ设为1 h。MEMS陀螺三轴数据各2 byte,则一个滑窗时间区间内所需存储及处理数据大小计算如式(5),约为10 MB。

Size=3 600 s×0.5 Hz×3×2 byte=10 800 byte

(5)

则该设计下,无需使用系统其他外存器件,中央处理器DSP片内缓存资源即可满足需求,且有较大余量。获得一个滑窗时间区间τ的陀螺数据后,通过ARMA(2,1)进行数学建模,建立陀螺数学模型。其中,a,b,c为待确定的ARMA系数。

yt=ayt-1+byt-2+cεt-1+εt

(6)

2.3 随机噪声滤波器设计

基于式(6)给出的时间序列模型,可得到如下EKF滤波器状态方程

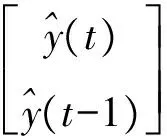
(7)

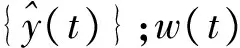
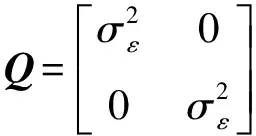
(8)

3 陀螺零偏及姿态估计器设计

该估计器由两个阶段组成。阶段1:仅在入轨初期使用。只依靠陀螺数据,通过姿态动力学模型快速地得到陀螺零偏的粗估计,为在线ARMA建模提供陀螺初始零偏;阶段2:陀螺、磁强计共同接入的滤波器收敛后使用。该滤波器可获得陀螺零偏的精估计,并作为新的陀螺零偏接入在线ARMA建模。同时,该滤波器能够得到卫星姿态信息。

经过随机噪声滤波后的陀螺数据,有助于提升陀螺+磁强计的姿态滤波器精度;同时更高精度的姿态滤波器又为随机噪声ARMA建模提供更精确的陀螺零偏估计值,形成协作互补,以进一步提升滤波系统精度。该估计器架构示意框图如图2所示。

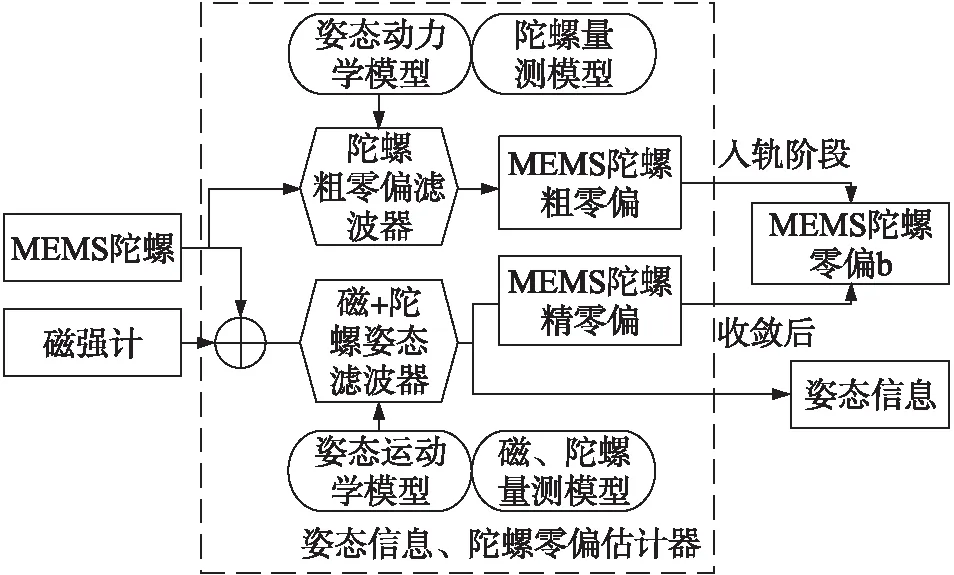
图2 陀螺零偏及姿态估计器设计框图

3.1 阶段1 仅基于陀螺的零偏粗估计器设计

该滤波器由姿态动力学、陀螺量测模型搭建,与卫星姿态、其余姿态敏感器无关,可通过陀螺原始采样数据快速地得到陀螺粗零偏的估计。此滤波器收敛速度快,仅用于入轨阶段。

微小卫星在轨道上运行时,姿态运动满足刚体姿态动力学方程[16]

(9)

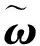
对式(9)在角速率标称值附近线性展开,可得

(10)

典型的MEMS陀螺量测模型表示如下

(11)

卫星入轨短时间自由翻滚阶段主动控制力矩为0,皮纳卫星体积小、重量轻,大气阻力、太阳光压、重力梯度干扰都较小,目前星体剩磁标定也能控制到较小的水平。采用陀螺的初测值作为卫星的初始角速率,即状态方程初值,则下一时刻由卫星姿态动力学递推的角速率与陀螺的实测值的差值,即为陀螺偏置信息。对式(9)在角速率标称值附近线性展开[17],再结合式(11)中陀螺零偏模型,得到系统状态方程:

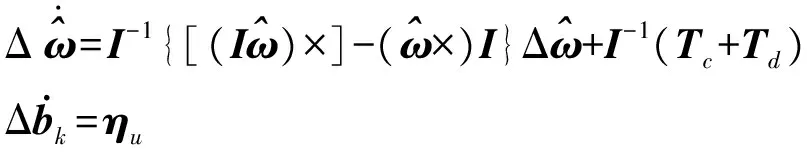
(12)

(13)

将式(11)线性化,所得小量方程为系统量测方程

(14)

此外,本文统一采用Δ表示物理量的估计误差,上标^表示物理量的估计值。

3.2 阶段2 陀螺+磁的姿态、零偏精估计器设计

该滤波器由姿态运动学、陀螺、磁强计量测模型搭建,最终获得卫星姿态信息、陀螺零点、磁强计零点的估计。

(15)

考虑陀螺和磁强计的测量模型

(16)

式中:bg为陀螺漂移;vu为陀螺角速度随机游走白噪声。式(15)、式(16)的组合为系统状态方程。

针对磁强计的测量结果组建误差量测方程

(17)

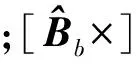
上述两个估计器的滤波流程在此不再赘述。

4 在轨组合滤波系统仿真

4.1 仿真背景及结果分析

基于浙江大学皮星二号轨道环境及在轨数据进行仿真验证。其中滤波器参数设置:vg取0.077 5,vu取0.000 145,vb取2e-8。MEMS陀螺在轨近3 h三轴原始采样数据如图3所示。

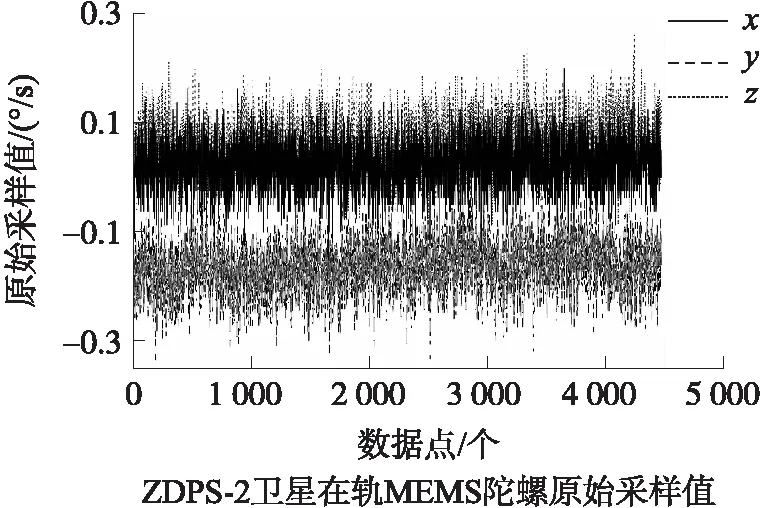
图3 浙江大学皮星二号MEMS陀螺在轨原始采样数据

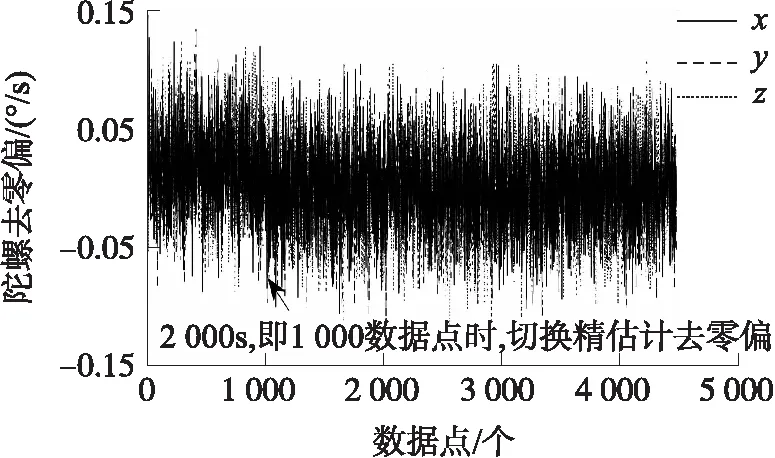
图5 皮星二号MEMS陀螺去零偏处理结果

图4为基于陀螺+磁强计组合的普通EKF算法与本文在轨滤波系统的陀螺零偏估计误差对比。其中粗零偏估计器在500 s内收敛,精度0.016 6 °/s;精零偏估计器、普通EKF算法都在2 000 s内收敛,精度从0.004 1提升至0.001 0 °/s,统计结果与最终姿态确定精度一同汇总于表3。设置2 000 s(即陀螺 1 000 数据点)为粗、精零偏补偿切换点,图5为陀螺去零偏处理结果,该结果接入随机噪声滤波器。

图4 普通EKF算法与本文滤波系统陀螺零偏估计结果对比

陀螺随机噪声滤波前后数据比较如图6所示,结果表明,本文建立的ARMA(2,1)模型能准确描述该MEMS陀螺的随机漂移特性,其构建的卡尔曼滤波器能有效减少陀螺随机噪声,参数抑制比皆在50%以上。近3 h数据滑窗ARMA建模数学表达式5组如下:

yt=0.027 25yt-1+0.058 96yt-2+0.437 2εt-1+εt

yt=0.029 27yt-1+0.056 12yt-2+0.466 5εt-1+εt

yt=0.029 33yt-1+0.055 37yt-2+0.465 8εt-1+εt

yt=0.029 17yt-1+0.056 45yt-2+0.467 3εt-1+εt

yt=0.029 42yt-1+0.055 82yt-2+0.466 8εt-1+εt

(18)

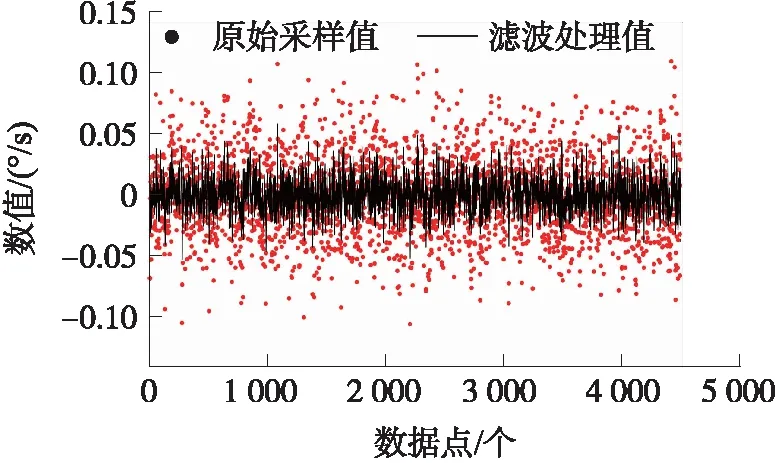
图6 MEMS陀螺随机噪声滤波前后比较

采用评估陀螺随机噪声的最佳方法Allan方差[3,6]进行滤波前后的比较分析,汇总如表2所示,其中主要参数包括量化噪声(QN),角度随机游走(ARW),零偏不稳定性(BI),速率随机游走(RRW),速率斜坡(DRR)。

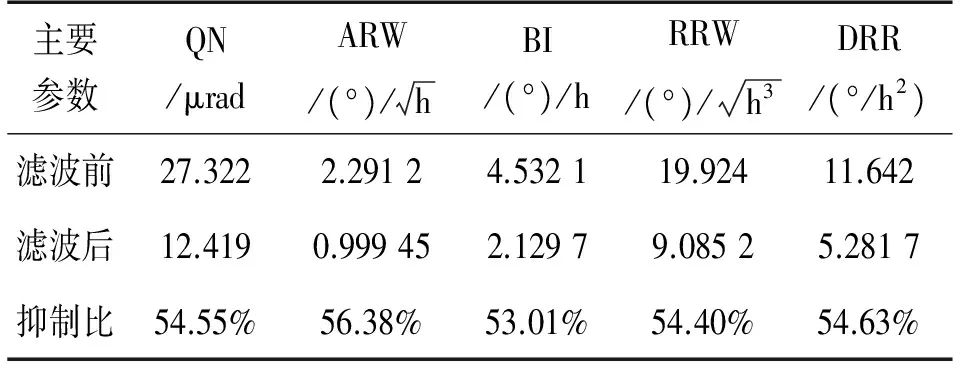
表2 滤波前后Allan方差主要项系数比较

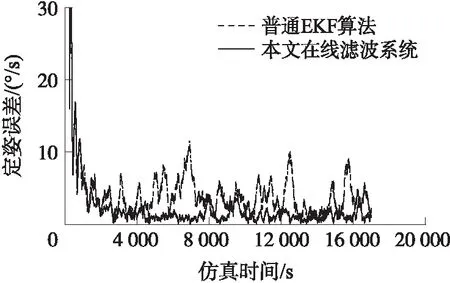
图7 陀螺+磁EKF算法与本文滤波系统定姿结果对比

图7为普通EKF算法与本文在轨滤波系统的最终姿态确定估计精度对比,统计结果汇总于表3。该结果表明,基于陀螺、磁强计的最小姿态敏感组合,本文所提系统方案的姿态确定精度1.21°(1σ),陀螺零偏估计精度0.001 °/s,较普通EKF算法有着显著提升,分别为190%以及310%。

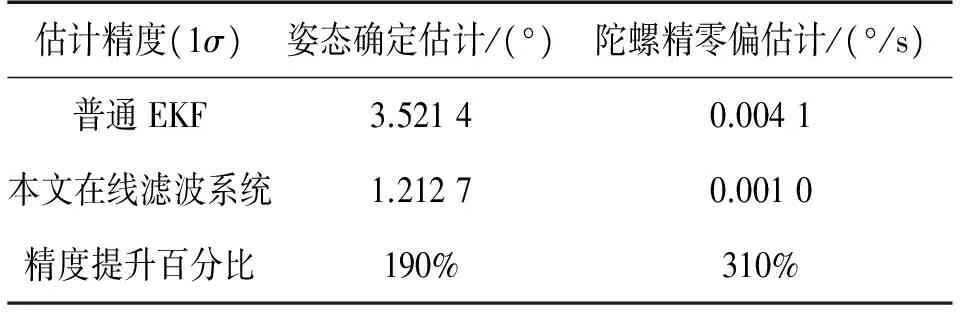
表3 陀螺+磁EKF算法与本文滤波系统估计误差汇总

5 结论

本文基于MEMS陀螺与磁强计最小姿态敏感组合,提出一种适用于皮纳卫星在轨运行的滤波系统方案。该方案通过在线滑窗ARMA建模降低陀螺随机噪声的误差,并由姿态滤波器估计所得的陀螺零偏去除常值分量对陀螺建模的影响。系统方案有效降低了陀螺随机噪声,较大程度提高了陀螺零偏估计、姿态确定精度,可满足中精度姿态控制的基本要求,是对皮纳卫星姿态确定最小系统精度提升及实用方案设计的有益探索。

[1] Springmann J C,Sloboda A J,Klesh A T,et al. The Attitude Determination System of the RAX Satellite[J]. Acta Astronautica,2012,75:120-135.

[2] 陈旭光,杨平,陈意. MEMS陀螺仪零位误差分析与处理[J]. 传感技术学报,2012,25(5):628-632.

[3] 张玉莲,储海荣,张宏巍,等. MEMS陀螺随机误差特性研究及补偿[J]. 中国光学,2016,9(4):501-510.

[4] 杜少鹤. MEMS陀螺仪组合系统及滤波算法设计[D]. 哈尔滨:哈尔滨工业大学,2015.

[5] 吕印新,肖前贵,杨柳庆. MEMS陀螺随机误差建模与补偿[J]. 电子测量技术,2012(12):41-45.

[6] 陈晨,赵文宏,徐慧鑫,等. 基于卡尔曼滤波的MEMS陀螺仪漂移补偿[J]. 机电工程,2013,30(3):311-313.

[7] 霍元正. MEMS陀螺仪随机漂移误差补偿技术的研究[D]. 南京:东南大学,2015.

[8] 蒙涛,王昊,李辉,等. MEMS陀螺误差建模与滤波方法[J]. 系统工程与电子技术,2009,31(8):1944-1948.

[9] 田颖,汪立新,李灿,等. 基于EEMD-RVM的陀螺漂移混合建模预测[J]. 传感技术学报,2015,28(10):1520-1524.

[10] 赵旭,苏中,马晓飞,等. 大温差应用环境下的MEMS陀螺零偏补偿研究[J]. 传感技术学报,2012,25(8):1079-1083.

[11] 王献忠. 陀螺与磁强计组合定姿及工程应用分析[J]. 航天控制,2009,27(5):43-47.

[12] 吴锦杰,刘昆,石实,等. 基于磁强计和光纤陀螺的小卫星姿态确定非线性滤波算法[J]. 国防科技大学学报,2013,35(1):1-6.

[13] Box G E P,Jenkins G M,Reinsel G C,et al. Time Series Analysis:Forecasting and Control[M]. John Wiley & Sons,2015.

[14] Diao Z,Quan H,Lan L,et al. Analysis and Compensation of Mems Gyroscope Drift[C]//Sensing Technology(ICST),2013 Seventh International Conference on. IEEE,2013:592-596.

[15] 王超. 光纤陀螺随机漂移的建模,分析和补偿[D]. 中国科学技术大学,2015.

[16] 章仁为. 卫星轨道姿态动力学与控制[M]. 北京:北京航空航天大学出版社,1998.

[17] 郁丰,刘建业,熊智. 用于微小卫星的陀螺随机常值偏置误差的在轨标定(英文)[J]. 南京:南京航空航天大学学报(英文版),2007,24(4):300-304.