基于DV-Hop测距修正的遗传模拟退火定位算法*

徐慧娟

(黄淮学院信息工程学院,河南 驻马店 463000)

目前,无线传感网络WSNs(Wireless Sensor Networks)已应用于多个领域,如森林防火监测、健康医疗等。而定位是WSNs应用的基础。现有的定位算法可分为基于测距(Range-based)[2]和基于非测距[3]两类。通常,基于测距定位算法的定位精度优于基于非测距定位算法。但是,后者无需额外的硬件设备,成本低,其中DV-Hop算法属典型的非测距定位算法,也被广泛应用。

然而,DV-Hop定位算法在测距过程中仍存在较大的误差,为此,研究人员提出了不同的改进算法。文献[4]利用粒子群算法求解定位方程,提高了定位精度;文献[5]提出基于差分进化的定位算法,其利用差分进化优化适应度函数,从而获取最优的位置估计。此外,文献[6-7]也分别提出基于遗传、人工蜂群的定位算法。但是,这些算法需要的参数较多,容易产生局部最优问题[1]。

本文提出基于DV-Hop测距修正的遗传模拟退火定位算法IDV-Hop-GSAL(Improved DV-Hop Ranging-based Genetic-Simulated Annealing Localizatio)算法。IDV-Hop-GSAL算法首先利用DV-Hop测距,即通过引用相近度修正测距值,然后利用最小二乘估计未知节点的位置(初始解),再利用遗传模拟退火算法优化初始解。实验数据表明,提出的IDV-Hop-GSAL算法降低了DV-Hop算法的定位误差,提高了定位精度。

1 DV-Hop测距原理及问题描述

1.1 DV-Hop测距原理

DV-Hop测距算法过程主要由3个阶段构成:

①估算跳数 在估算跳数阶段,锚节点广播自己位置以及初始跳数信息,使得邻居节点能够获取离锚节点的跳数值。此阶段是DV-Hop的初始阶段。

②计算锚节点间的平均跳距 通过估算跳数阶段,锚节点已获取了各锚节点的跳数以及位置信息[8]。据此,计算平均跳距。假定锚节点i计算的平均跳距:

(1)

式中:dik表示锚节点i与锚节点k间的距离。相应地,hik为它们间的跳数。而(xi,yi)和(xk,yk)分别表示锚节点i、k间的位置。

③测距 锚节点计算了平均跳距后,就将平均跳距值进行广播。未知节点接收后,就利用此值计算离锚节点间的距离[9]。假定未知节点j离锚节点k的距离为djk,其定义如式(2)所示:

djk=Hopsizek×hjk

(2)

式中:hjk为节点j与节点k间的跳数。

DV-Hop测距示例如图1所示。

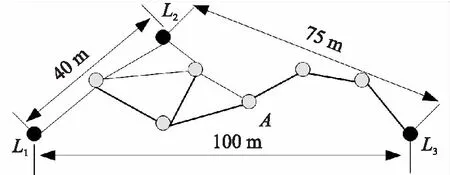
图1 DV-Hop测距原理

图1中的3个黑色实心圆表示锚节点,其他节点为待定位节点(未知节点)。以锚节点L2为例,在估算平均跳距前,先计算离另两个锚节点(L1、L3)距离和跳数,最后依据式(1)计算平均跳距:

Hopsize2=(40+75)/(2+5)=16.43m

(3)

随后,锚节点L2就广播平均跳距值。未知节点A接收后,就依据式(2)计算离3个锚节点的距离:

(4)

1.2 问题描述

从1.1节过程可知,DV-Hop测距是利用锚节点所计算的平均跳距与跳数相乘而得到的距离。而平均跳距是由锚节点依据锚节点的分布情况进行计算的。如果锚节点分布不均匀,必然会存在大的误差。为此,本文对测距值进行修正。在获取了修正后的测距值后,再利用遗传模拟退火算法GASA进行位置估计,进而提高位置估计。

2 IDV-HOP-GSAL定位算法

2.1 系统模型

2.2 测距值的修正

由2.1节可知,未知节点在估算离各锚节点间的距离时,是采用同一个平均跳距值与离各锚节点间的跳数相乘。这没有考虑各锚节点周围节点分布的差异性,必然会引起测距误差[10]。

以图2为例。假定A是未知节点。B、C、D为锚节点。从图2可知,节点A离锚节点B、C均是一跳。依据式(2)计算,节点A离锚节点B、C距离是相等的。而实际上,它们的距离并不相等。

图2 节点通信示例

此外,如果节点A是从锚节点B获取了平均跳距HopsizeB。若HopsizeB值误差较大,则节点A在估算到其他锚节点距离时,就会产生测距误差,并且随跳数增加而被累积。显然,在利用单一平均跳距进行测距时,增加测距误差。因此,必须对测距值进行修正。

为此,提出的IDV-HOP-GSAL定位算法先对测距值进行修正。具体而言,未知节点先计算离各锚节点的距离远近,再依据远近程度对测距值进行修正。

(5)

式中:λjk表示未知节点j离它的邻居锚节点k的相近度。而Setj、Setk分别表示节点j、k的邻居节点集。相应地Crad(Setj∪Setk)、Crad(Setj∩Setk)分别表示Setj和Setk两个集的并集、交集的元素个数。

相近度能够真实地反映节点离邻居锚节点的远近信息。以图3为例进行说明。从图3可知,Crad(SetA∪SetB)=21、Crad(SetA∩SetB)=7。因此,依据式(5)计算可得:节点A与B的相近度λAB=21/7=3。类似地,λAc=17/12≈1.42。由于λAB>λAC,说明节点C离节点A更近,而节点B离节点A更远,其更接近于通信半径R。

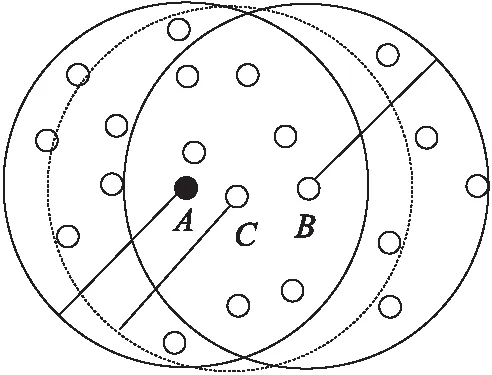
图3 计算相近度示意图

依据相近度,未知节点便可对距离进行修正。假定未知节点j对距离djk修正后:

(6)

式中:λkmax表示节点k的所有邻居节点离自己相近度的最大值。

2.3 定位算法

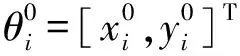
整个定位算法的思路就是:先通过DV-Hop测距并进行修正,然后再利用最小二乘法估计未知节点的初始位置,最后将此初始解作为GSAS的输入[11],并进行全局搜索。再经历遗传算法内的选择、交叉、变异等一系列操作,产生新的个体,然后再基于新个体进行模拟退火操作,其结果作为下一代群体中的个体。

(7)

然后,再建立函数fk:

(8)

因此,fk表示锚节点k与未知节点i的定位误差。为了最小化误差,并且避免“早熟”情况,减少个体适应度间的差异,使得群体具有多样性。据此,建立适应度[12]:

(9)

式中:βk表示权值,其反映了未知节点与锚节点间测量值的精度。IDV-HOP-GSAL算法就是利用GSAS降低适应度值,适应度值越小,定位越准确。

为了更准确地估计未知节点位置,对GSAS的参数进行控制。首先利用式(10)更新种群,进而更新染色体的好坏。

min{(p,exp(fk-f′)/Tt)}>random(0,1)p=1

(10)

从式(10)可知,更新种群的原则:将当前种群中最佳染色体直接复制到子代种群中。式(10)中fk、f′分别表示子代中个体适应值、父代中个体适应值最差的个体。而Tt为控制温度,单位度(℃)。

然后,通过Metropolis准则来检测是否对解进行了更新。假定xi是本次解,xi+1是新解,且其以概率p进行更新:

(11)

式中:T温度参数。依据文献[13],初步将T设置为90。

最后,进行交叉、变异操作。在交叉操作时,将选择的点的序列分为左、右部,同时使得两个基因的左、右部的序列进行互换。然后,依据交换变异策略进行变异操作,进而维持种群的多样性,最终增强全局探索能力。

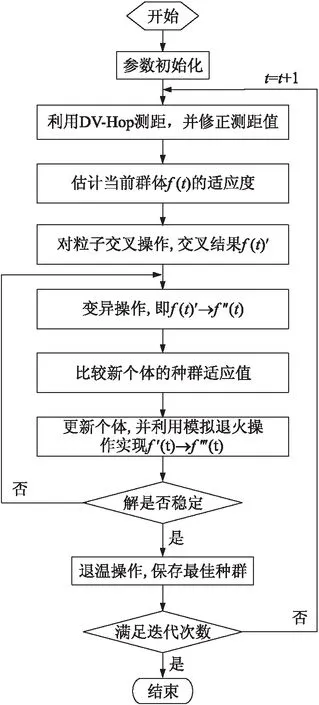
图4 IDV-HOP-GSAL定位算法流程

IDV-HOP-GSAL定位算法流程如图4所示。首先进行初始化阶段。在此阶段,设定初始值,包括初始迭代次数t=0、变异概率、交叉概率以及T0和Td,其中T0、Td分别表示初始温度、终止温度。然后,利用DV-Hop测距,直到迭代次数满足要求。

3 仿真与分析

3.1 仿真环境

利用MATLAB建立仿真平台,分析IDV-HOP-GSAL定位性能。迭代次数为100、交叉概率为0.008、变异概率为0.000 6,而种群大小为30。此外,仿真过程过程中考虑锚节点数、节点通信半径以及总的节点数对平均定位误差的影响,为此,设为3个独立实验。平均定位误差的定义如式(12)所示:

(12)

为了更好地的比较IDV-HOP-GSAL的定位算法,选择几个同类的定位算法进行比较:①利用DV-Hop测距(未修正),最小二乘法定位,记为DV-Hop+LS;②布谷鸟改进的DV-Hop算法,记为CSDV-Hop。

3.2 仿真数据

3.2.1 实验一

首先分析锚节点数对平均定位误差的影响。实验参数如下:总的节点数为100(锚节点和未知节点),其中锚节点比例从5%～35%变化。此外,通信半径R=30 m。实验数据如图5所示。

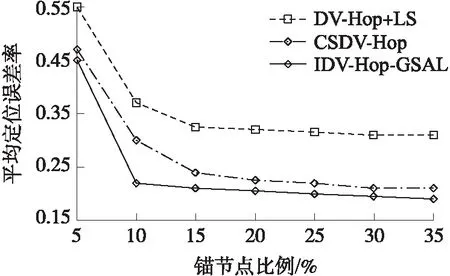
图5 锚节点数对平均定位误差率的影响

图5是DV-Hop+LS定位算法、CSDV-Hop和IDV-Hop-GSAL定位算法运行了50次的平均定位误差随锚节点变化曲线。从图5可知,当通信半径R、总的节点数固定时,DV-Hop+LS、CSDV-Hop和IDV-HOP-GSAL定位算法的平均定位误差随锚节点数的增加而减少。换而言之,锚节点数的增加有利于定位精度的提高。与DV-Hop+LS、CSDV-Hop算法相比,提出的IDV-HOP-GSAL算法的平均定位误差得到有效地控制,且分别比DV-Hop+LS、CSDV-Hop下降了25%、6%。

3.2.2 实验二

本次实验分析通信半径R对平均定位误差的性能。实验参数如下:通信半径R从20 m～50 m变化,总的节点数为100,锚节点数为30。图6描述了DV-Hop+LS、CSDV-Hop和IDV-HOP-GSAL定位算法运行了50次的平均定位误差随通信半径R的变化曲线。

图6 通信半径R对平均定位误差率的影响

从图6可知,通信半径R的增加,降低了平均定位误差,提高了定位精度。原因在于:通信半径越长,跳数越短,这有利于测距的精度的提高。与DV-Hop+LS、CSDV-Hop算法相比,提出的IDV-HOP-GSAL算法的平均定位误差得到下降,且分别下降了28%、5%。这主要归功于IDV-HOP-GSAL算法利用相近度对测距值进行了修正,同时也利用GSAS算法估计了未知节点位置。

3.2.3 实验三

最后,分析节点数对平均定位误差的影响。实验参数如下:锚节点数为30、通信半径R=30 m,总的节点数从60～180变化,步长为20。图7描绘了DV-Hop+LS、CSDV-Hop和IDV-Hop-GSAL算法运行50次的平均定位误差曲线。

图7 节点数对平均定位误差率的影响

从图7可知,当锚节点数不变、通信半径R=30 m固定时,节点数的增加,降低了平均定位误差,但下降幅度逐渐下降。与DV-Hop+LS、CSDV-Hop算法相比,提出的IDV-HOP-GSAL定位算法的平均定位误差得到控制,且比DV-Hop+LS、CSDV-Hop算法下降了30%、4.7%。

3.2.4 算法复杂度

表1描述了在100个节点数、30个锚节点以及通信半径R=30 m的环境下的算法运行时间。从表1可知,提出的IDV-HOP-GSAL定位算法的运行时间高于DV-Hop+LS算法。这也说明,IDV-HOP-GSAL定位算法以一定的复杂度换取高的定位精度。

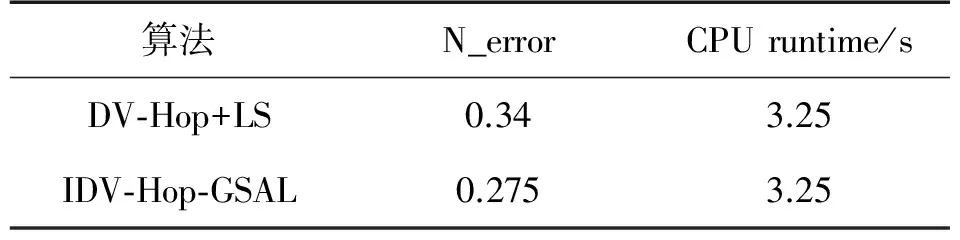
表1 算法的运行时间

4 总结

本文针对传统的DV-Hop的定位算法,先分析它的不足,再提出基于DV-Hop测距修正的遗传模拟退火定位算法 IDV-Hop-GSAL算法。IDV-Hop-GSAL算法利用节点分布情况,对测距值进行了修正。在定位阶段,先利用最小二乘法估计未知节点位置,并将其作为初始值,然后再GSAL算法优化初始值。实验数据表明,提出的IDV-Hop-GSAL算法的定位精度优于DV-Hop+LS算法。在后期,将优化算法,降低算法的复杂度。

[1] 刘登峰,章力,邴晓瑛,等. 基于布谷鸟差分算法优化的DV-Hop改进算法[J]. 系统仿真学报,2017,29(4):790-797.

[2] Chu Y L,Tzeng J R,Cheng Y P. Density-Adaptive Range-Free Localization in Large-Scale Sensor Networks[C]//41st International Conference on Parallel Processing Workshops(ICPPW),2012. USA:IEEE,2012:488-495.

[3] Maung N,Kawai M. Experimental Evaluations of RSS Threshold-Based Optimised DV-HOP Localisation for Wireless Ad-Hoc Networks[J]. Electronics Letters(S1350-911X),2014,50(17):1246-1248.

[4] 黄艳,臧传治,于海斌. 基于改进粒子群优化的无线传感器网络定位算法[J]. 控制与决策,2012,27(1):156-160.

[5] 林雯,张烈平,王守峰. 基于差分进化算法的无线传感器网络节点定位方法研究[J]. 计算机测量与控制(S1671-4598),2013,21(7):2023-2026.

[6] 刘彦隆,吕显朋,王相国. 混合遗传算法在WSNs定位中的应用[J]. 传感器与微系统,2014,33(2):150-153.

[7] 李牧东,熊伟,梁青. 基于人工蜂群改进算法的无线传感网络定位算法[J]. 传感技术学报,2013,26(2):241-245.

[8] 向满天,王胜,杨友华. 基于阈值机制与距离校正的WSN改进DV-Hop定位算法[J]. 传感技术学报,2016,29(6):920-926.

[9] 张新荣,熊伟丽,徐保国. 采用RSSI模型的无线传感器网络协作定位算法[J]. 电子测量与仪器学报,2016,30(7):1008-1017.

[10] 任克强,李亚东. WSN中DV-Hop节点定位算法的改进[J]. 传感技术学报,2017,30(4):611-618.

[11] 李腾宇,易晓梅,陈石. 基于RSSI加权质心和GASA优化的WSN定位算法[J]. 计算机工程与应用,2017,53(6):118-123.

[12] Tian Jun. Reversible Data Embeding Using a Difference Expansion[J]. IEEE Trans on Circuits and Systems for Video Technology,2013,13(8):56-62.

[13] Wu H C,Lee C C,Tsai C S. A High Capacity Reversible Data Hiding Scheme with Edge Prediction and Difference Expansion[J]. Journal of Systems and Software,2014,82(12):1966-1973.