粒子计数器的一种新型光学传感器设计*

石 鑫,韩 月,丁思红,戴 兵*

(1.南通大学机械工程学院,江苏 南通 226019;2.南通大学理学院,江苏 南通 226019)

光学粒子计数器以其检测速度快、结果可靠[1-3]而受到国内外学者重视。粒子计数器的关键部件是光学传感器,按散射光接受方式可分为[1-7]前向接受系统(最大采样角范围:±3°～±30°),如库尔特仪、ROYCO粒子计数器;侧向接受系统(最大采样角范围:+75°～+105°),如ROYCO粒子计数器;半旋转二次曲面集光镜(最大采样角范围:±35°～±135°),如Climet、国产Y09激光粒子计数器。但是,上述仪器存在两个方面的问题[1-2,5-7],一是接受角范围存在一定的局限性,导致检测信号易受颗粒形状及折射率的影响。二是由于目前仪器流行采用便携的半导体激光光源,造成光敏区光强均匀性不佳,导致检测信号易受颗粒在光敏区位置的影响。所以,已有的仪器精度有限,重复性不佳。为此,本文设计了一种新型的光学传感器,利用旋转对称椭腔镜扩大空间角的接受范围,采用非球面透镜与柱面透镜组合光学器件提高光敏区光强的均匀性。通过模拟计算证实该光学传感器的适用性优良,改善了目前已有仪器的不足,同时具有简洁、便携、价廉的特点。

1 光学接受系统的设计

粒子计数器是采用光电接收器件接受单颗粒在光照射后产生的散射光信号量值来反映颗粒大小的一种检测技术[1-3],为了保证接受的光信号大小能反映粒度大小,确保仪器的精度及灵敏度,如何减小折射率、颗粒形状对测量的影响是光学接受系统的设计要点。本研究设计了旋转对称椭腔镜光接受系统,可以达到上述目的。

1.1 旋转对称椭腔镜系统

图1为旋转对称椭腔镜及其内颗粒光散射示意图,这里,F1为椭腔镜的左焦点,F2是右焦点。当入射光照射到处于F1位置(光敏区)的颗粒时,颗粒向各方向发出的散射光必将最终聚于椭腔镜的右焦点F2,在焦点F2接受的光信号实际上是来自于大空间角范围内的散射光,其方位角φ涵盖了0～360°的范围,而散射角θ的范围可达±5°～±155°。与已有的光接受系统[1-7]相比,该系统散射光的接受空间角范围有了较大的增加。

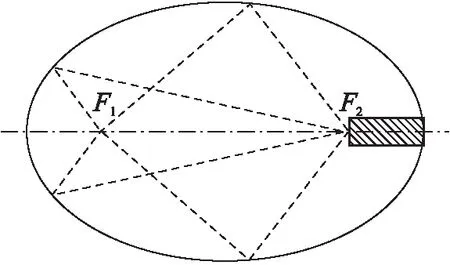
图1 旋转对称椭腔镜接受系统示意图

1.2 颗粒光散射及其通量的基本理论

颗粒的光散射理论是粒子计数器的光学传感器依赖的基本原理。球形颗粒是最简单的颗粒模型,其散射问题由Mie散射理论[8]给出。但是实际颗粒经常是非球形的,近年来,发展了T矩阵法、离散偶极子近似法(DDA)等[9-14],可解决一些具有对称性的非球形颗粒散射问题,其中,T矩阵法是目前公认的最为有效的方法。

1.2.1 非球形颗粒的T矩阵散射理论

当波长为λ的入射光入射到任一轴对称颗粒时,其入射场和散射场按球矢量波函数展开为[9-10]:

(1)

(2)

(3)

(4)

(5)

(6)

式(5)和式(6)可写成:

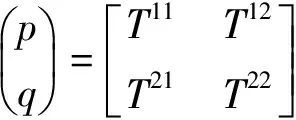
(7)

式(7)称为T矩阵,构成了入射场扩展系数与散射场扩展系数之间的关系。

入射光及散射光的斯托克斯矢量关系为[12-14]:

(8)

这里,对轴对称颗粒,Mueller矩阵F(θ)为

(9)

若颗粒为椭球形颗粒,则其形状方程为[12-14]:

r(θ,φ)=reqβ1/3(β2cos2θ+sin2θ)-1/2

(10)

这里,req为等体积球的半径,β=b/a为形状率[13-14],b,a分别为椭球的长半轴及短半轴,当β=1时,该颗粒为球形颗粒。

1.2.2 散射光通量

粒子计数器的光电接收器接受的光能量与接受空间角范围内的颗粒散射光通量成正比,该通量是散射光强在接受面上的积分,设该接受面对应的散射角范围是θ1到θ2。由斯托克斯参数可得到颗粒光散射的强度函数i1(θ),i2(θ)[11-13],则接受面上光通量FL为:

(11)

(12)

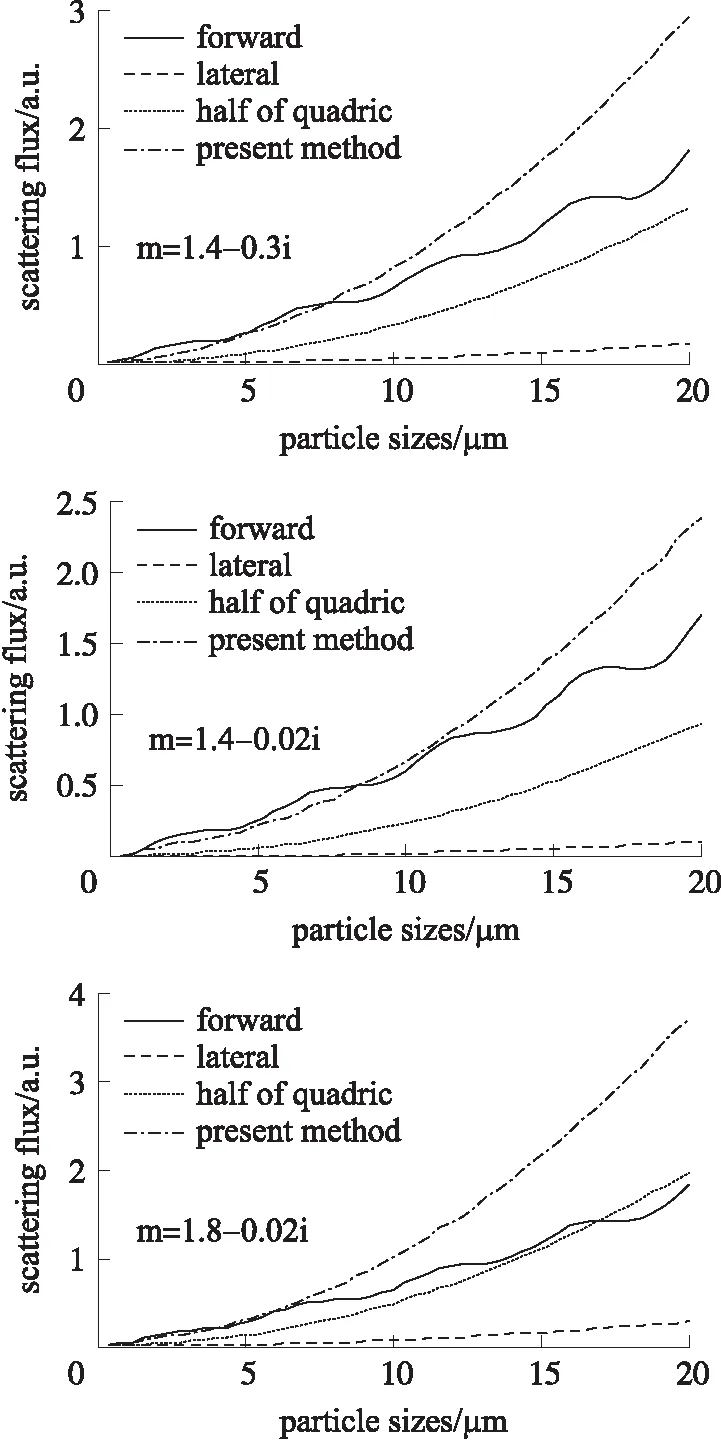
图2 不同折射率下(m=1.40-0.3i,1.40-0.02i,1.80-0.02i),球形颗粒散射光通量随粒径的变化

1.3 模拟计算

为了说明本接受系统减小折射率、颗粒形状影响的效果,在不同折射率、不同形状及不同空间取向下,基于T矩阵散射理论及式(12)、式(13)模拟计算了本系统接受的散射光通量随粒径的关系,为了对比,同时也给出了前向、侧向、半旋转二次曲面3种典型接受系统的结果。计算中,对于非球形颗粒情况,以椭球形颗粒为例。

图2是不同折射率下接受的球形颗粒的光通量随粒径的关系。这里,入射光波长取450 nm(下同),折射率取1.40-0.3i、1.40-0.02i、1.80-0.02i,分别反映了折射率虚部及实部不同的情况,其中虚部大小取0.3及0.02分别表示强吸收及弱吸收[8]。

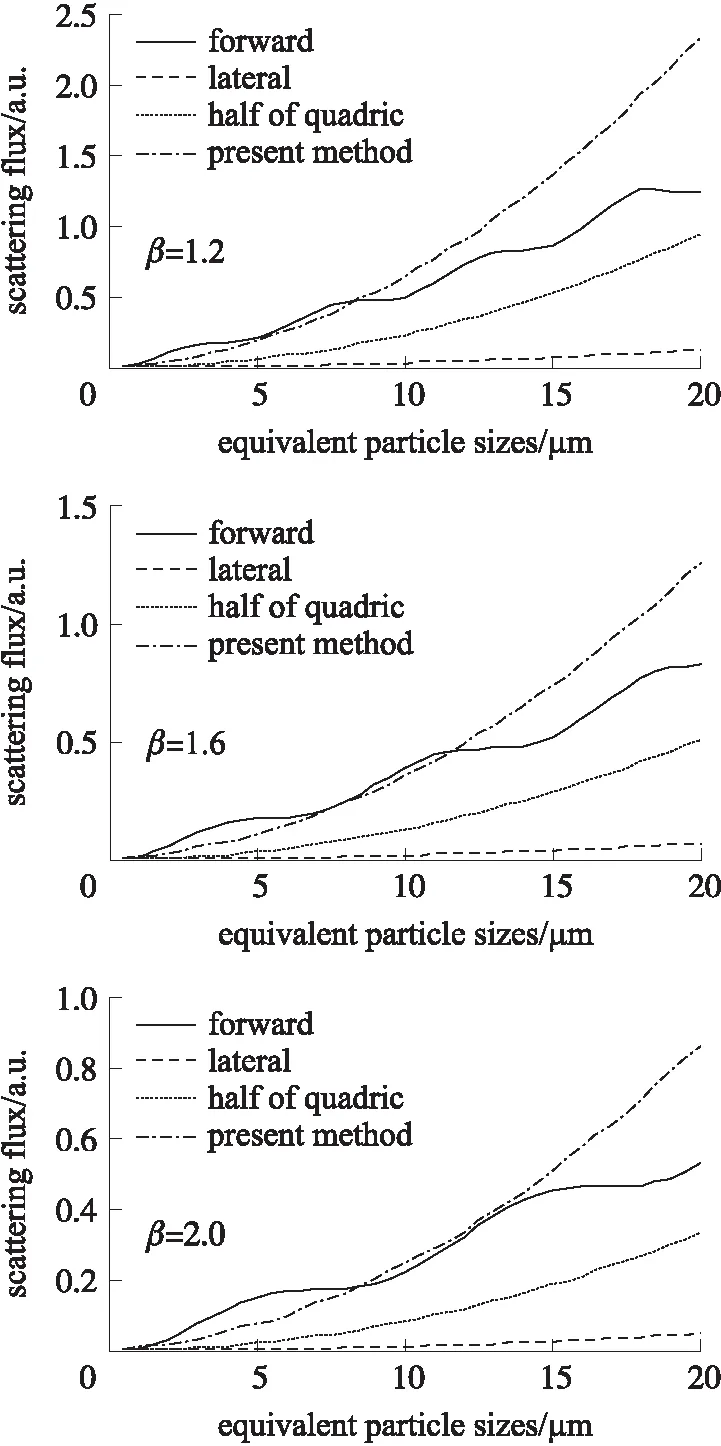
图3 不同形状率下(β=1.2,1.6,2.0),椭球形颗粒散射光通量随粒径的变化

图3是不同形状率下,接受的椭球形颗粒的散射光通量随等效粒径的关系,这里折射率m取1.45-0.1i,椭球形颗粒取向的方位角为:θ0=15°,φ0=30°,椭球的3种形状率分别为:1.2,1.6,2.0。图4是不同空间取向下,接受的椭球形颗粒的散射光通量随等效粒径的关系,这里折射率m取1.55-0.05i,椭球形颗粒的形状率为β=1.5,椭球的3种取向方位角分别为:θ0=30°,φ0=45°;θ0=30°,φ0=75°;θ0=60°,φ0=75°。由图2～图4可见,在不同折射率、不同形状率及不同空间取向下,本系统接受的光通量与粒径的关系曲线单调性优良,较前向接受系统有了明显改善,表明本系统利用光通量大小来反映粒度大小具有更佳的适用性,可减小折射率、颗粒形状造成的影响,提高测量精度。此外,还可见,对不同折射率及不同形状的颗粒,本系统接受的光通量量值较已有接受系统明显增大,特别是比侧向接受系统有大幅增加,表明本系统将具有更高的灵敏度。

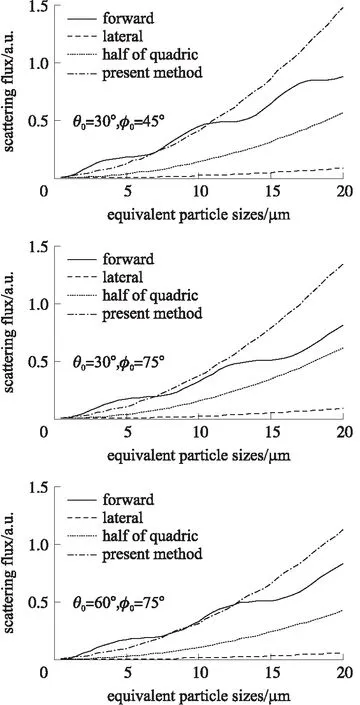
图4 不同空间取向下(θ0=30°,φ0=45°;θ0=30°,φ0=75°;θ0=60°,φ0=75°),椭球形颗粒散射光通量随粒径的变化

2 光强均匀化系统的设计

当光束照射到颗粒时,散射光强将随入射光强不同而不同,所以如果颗粒处在光敏区不同位置,且光敏区光强不均,势必会对测量结果造成影响。激光束呈高斯分布,如果不加以均匀化处理而直达光敏区,将会由于上述原因带来系统误差。光强均匀化方法较多[15-16],如二元光学元件、液晶空间光调制器等,由于设计的目标不同,方法也有所区别。基于已有文献的思想[15-16],以光敏区均匀性为主要目标要求,从易加工及经济的角度出发,考虑到目前非球面加工已经成为一项成熟技术,本研究采用非球面透镜与柱面透镜组合光学器件,可以达到上述目的。

2.1 非球面-柱透镜组合系统

非球面透镜与柱面透镜组合光学器件布局如图5所示,半导体激光器发出的光束首先入射到一非球面透镜然后再经过一柱面透镜,由于半导体激光束在快轴方向受到柱面的进一步汇聚,所以在光敏区形成光强均匀度较高且能量聚集的光束。

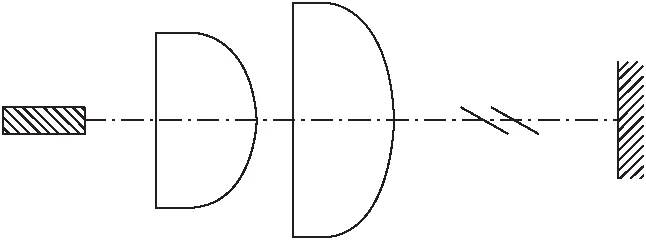
图5 非球面-柱面透镜组合系统示意图

2.2 模拟计算

为了说明上述组合光学器件的光均匀化效果,以Zemax进行模拟。Zemax中有很多优化设计操作数,分别代表光学设计中所需求的光学特性、像差等约束和目标。为了最优化光学设计,建立评价函数,其可由式(14)表示[15-16]:

(14)

这里,Vi是第i种操作的实际值,Ti是第i种操作的目标值,Wi是第i种操作的权重。本研究的主要目标是能量的均匀性,对成像质量要求不高,所以采用光照度评价函。在Zemax中,利用光线坐标追迹法进行模拟。这里,设光学系统的轴线方向为z,光源的位置为原点,其他各光学元件轴向位置坐标、通光半径、中心厚度分别如表1所示。

表1 各光学元件的光学参数

半导体激光器功率设为200 mW,快轴与慢轴方向发散角分别设为40°及10°,发出的光波长仍选为450 nm。透镜材料选用冕牌玻璃(K9°),其折射率n=1.516 3。非球面及柱面表达式分别为:

(15)

z2=-ν1y2-ν2y4-ν3y6-ν4y8

(16)

这里,μ1,μ2,μ3,μ4及ν1,ν2,ν3,ν4为常数。模拟得到的光照度分布如图6所示,结果显示,在径向半径约1.0 mm范围内,光强分布明显被平顶化,激光束的高斯分布特征基本消失,同时光强也表现出很好的汇聚度。经计算,在光敏区(半径为0.6 mm的区域)范围内,光照度的均匀度为92.3%,说明经此设计后光敏区内已经具有了较好的光强均匀性,可确保在光敏区的不同位置,入射光强基本相等,消除了因光敏区位置差别造成的系统误差。

图6 光束均匀化后的光照度分布

3 传感器整体结构

传感器整体结构如图7所示。旋转对称椭腔镜外框由金属制成,腔壁内表面经抛光处理并镀有反射膜。半导体激光器及其均匀化透镜组被固定在一金属圆柱形腔内,其外框再固定在椭腔镜外框上。激光束经图7所示的光路入射到旋转对称椭腔的左焦点(光敏区),在该焦点处与采样粒子流相遇,直射光束进入光陷阱被湮没,散射光经椭腔镜面聚于右焦点,并被该焦点后的探测器接受,检测信号可经输出、放大、处理。气路通道如图8所示,采样气流由进气道导入经出气道流出,进出气道在一条直线上,其中间区域是光敏区,进气道外裹一同轴纯净气道,起到稀释气流并防止颗粒残留腔内的作用,整个气路通道垂直于图7所示的平面并通过左焦点。

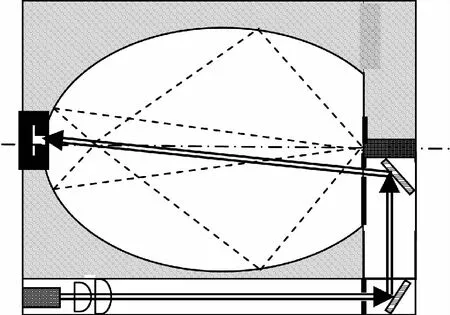
图7 光学粒子计数器传感器整体结构示意图

图7中采取了2条措施抑制杂散光,一是设置了3个光阑,2个在入射光路上,1个在探测器前,二是采用椭腔镜内除了进出气通道外别无其他硬件的设计。本传感器整体结构在设计上不仅满足了扩大空间接受角及均匀化光敏区光强的主体目的,同时也贯穿了结构紧凑、易于加工、方便携带、造价低廉的设计理念。

4 实验验证

由于非球形粒子目前仍没有标准样本(包括形状和等效粒径),故对非球形粒子的实验验证及校准目前难以实现。为此,本研究仅对球形标准粒子进行了部分实验验证,实验框图如图9所示。

图9 检测传感器的实验结构框图

采用PG-100粒子发生器雾化和干燥标准粒子稀释液(球形标准粒子悬浮液),经分配器后通过抽气通道进入待测传感器,接受光电管将光信号转变成电信号,其经放大电路等分别进入示波器及数据采集卡。标准粒子采用北京博研科创公司生产的3种粒度的聚苯乙烯(PSL)微球,标号分别为:GBW 120064(0.117 μm)、GBW12010a(0.333 μm)及GBW 120060(1.098 μm)。表2给出了测得的本传感器对3种标准粒子产生的脉冲幅值电压均值,为了对比,也给出了国产粒子计数器所采用的半旋转传感器的实验结果。

表2 传感器测得的3种粒度粒子产生脉冲的幅值电压

由表2可见,本传感器对不同粒度的粒子产生的脉冲幅度值均有明显增加,这对提高信噪比非常有利。更为有利的是,对于0.117 μm的粒子,国产传感器产生脉冲的幅值电压为76 mV,但由于该类传感器的背景噪声幅度约为50 mV,所以不易甄别真实信号,而本传感器产生脉冲的幅值电压为141 mV,则可以轻松地甄别真实信号。上述实验结果表明,本传感器的性能较同类传感器有了显著提升,可提高仪器的信噪比,扩展检测下限。

5 结论

①T矩阵理论计算表明,扩大颗粒散射空间接受角,可以减小颗粒折射率、形状及空间取向对测量的影响。

②非球面透镜与柱面透镜组合光学系统,可提高半导体激光束光强分布的均匀性,可减小颗粒在光敏区位置不同对测量的影响。

③基于旋转对称椭腔镜并采用非球面透镜与柱面透镜组合光学器件的光学粒子计数器传感器,可扩展空间接受角,增加光敏区光强均匀性,提高传感器的精度及灵敏度。

④实验验证表明,本传感器比同类传感器有更好的性能,且由于简洁、便携、价廉的优点,应用前景广阔。

[1] 叶超,孟睿,葛宝臻. 基于光散射的粒子测量方法综述[J]. 激光与红外,2015,45(4):344-348.

[2] Villa S,Sanvito T,Paroli B,et al. Measuring Shape and Size of Micrometric Particles from the Analysis of the Forward Scattered Field[J]. J Appl Phy,2016,119(22):224901.

[3] Yoshida H,Igushi T,Yamamoto T,et al. Theoretical Calculation of Fundamental Uncertainty Region Based on the Maximum and/or the Minimum Size in the Preparation of Standard Reference Particles for Particle Size Measurement[J]. Advanced Powder Technology,2011,22(1):43-49.

[4] Yoon J,Kim M,Lee S,et al. A Real-Time and in Situ Particle Size Distribution Measurement for Fractal-Like Diesel Exhaust Particles[J]. Journal of Aerosol Science,2015,90:124-135.

[5] Sipelgas L,Raudsepp U. Comparison of Hyperspectral Measurements of the Attenuation and Scattering Coefficients Spectra with Modeling Results in the North-Eastern Baltic Sea[J]. Estuarine Coastal and Shelf Science,2015,165:1-9.

[6] 张加宏,韦圆圆,顾芳. 高精度光散射气溶胶质量浓度测量系统的信号处理研究[J]. 传感技术学报,2016,29(4):536-544.

[7] Kulikov K G,Koshlan T V. Measurement of Sizes of Colloid Particles Using Dynamic Light Scattering[J]. Technical Physics,2015,60(12):1758-1764.

[8] Van de Hulst H C. Light Scattering by Small Particles[M]. New York:Wiley,1957:119-130.

[9] 张学海,魏合理,戴聪明,等. 取向比对椭球气溶胶粒子散射特性的影响[J]. 物理学报,2015,64(22):224205-1-10.

[10] Huang Xin,Yang Ping,Kattawar George. Effect of Mineral Dust Aerosol Aspect Ratio on Polarized Reflectance[J]. J Quantiitative Spectroscopy and Radiative Transfer,2015,151:97-109.

[11] Wu Y Q,Yang M L,Sheng X Q,et al. Computation of Scattering Matrix Elements of Large and Complex Shaped Absorbing Particles with Multilevel Fast Multipole Algorithm[J]. J Quantiitative Spectroscopy and Radiative Transfer,2015,156:88-96.

[12] Mishchenko M I,Martin P A. Peter Waterman andT-matrix Methods[M]. J Quantiitative Spectroscopy and Radiative Transfer,2013,123:2-7.

[13] 戴兵,袁银男,梅德清,等. 椭球模型下通过雾场的多重光散射谱[J]. 物理学报,2012,61(8):084201-1-084201-7.

[14] Farafonov V G,Ustimov V I. Properties of the T Matrix in the Rayleigh Approximation[J]. Optics and Spectroscopy,2015,119(6):1022-1033.

[15] 梁丹华,孙华燕,樊桂花,等. 半导体激光阵列光束整形技术研究进展[J]. 装备制造技术,2014,12:179-181.

[16] 战利伟. 半导体激光器输出光束整形设计[D]. 长春:长春理工大学,2011.