一种具有交叉缠绕激励绕组的磁通门电流传感器

杨晓光,金双双,高灵虎,徐林亮,高丽敬

(河北工业大学省部共建电工装备可靠性与智能化国家重点实验室,天津 300130)

随着电力电子技术的发展,对电流传感器性能的要求不断提高,从而使得电流传感器迅速发展。电力电子装备中需要测量的电流形式多种多样,有不同的波形、频率和测量范围。针对不同的电流形式,需要不同类型的检测方法和电流传感器。目前已经报道了很多新的电流检测方法和新型结构的电流传感器[1-2]。电流检测技术和方法可分为非隔离式与电隔离式两种。非隔离式主要是指分流电阻;电隔离式主要包括电流互感器、霍尔电流传感器、罗氏线圈、巨磁阻电流传感器以及磁通门电流传感器等[3-7]。其中磁通门技术基于检测磁路的饱和特性而设计,具有低温漂、低漂移、高精度及高灵敏度等优势[8]。

国际上已经公开了磁通门电流传感器的各种结构和检测方法:Guillermo Velasco-Quesada等人设计了一种包含3个磁芯的磁通门电流传感器,设计了功率转换器以减小功耗。Eyal Weiss等人设计了一种正交磁通门电流传感器,减小了磁通门的噪声。Piotr Frydrych等人介绍了一种小型双轴磁通门电流传感器,进一步实现了磁通门传感器的小型化[10]。庞娜等人通过对激励源幅值位置的时间变化进行测量,提高了测量精度和灵敏度[11]。Wang Nong等人为实现直流大电流测量引入了自激振荡式半数字化磁通门电流传感器,这一功能的实现主要依靠磁通门开环原理,应用微控制器对激励电压的占空比进行测量[12]。

磁通门电流传感器容易受到激励源带来的外界磁场的干扰。Guillermo Velasco-Quesada等人采用激励绕组差分的形式,减小激励源带来的外界磁场的干扰。由于变压器效应,高频激励源会耦合到反馈绕组和原边绕组中对磁通门传感器产生噪声干扰[1,13-14]。为了降低外部磁场和内部磁场造成的干扰,磁通门电流传感器可以使用额外的磁芯和额外的线圈[13-14],或者绕组采用正交分布[15]。

前期工作中我们采用聚磁芯或者U型聚磁壳来降低外界磁场干扰[16-18];采用激励绕组与被测绕组、感应绕组缠绕的方向垂直的方法消除激励电压引起的噪音[1]。

本文提出了一种激励绕组具有交叉缠绕结构的磁通门电流传感器。该缠绕方式有利于降低激励源耦合到反馈绕组和原边绕组的噪声,提高传感器的测量精度与灵敏度。

1 电流传感器的结构与工作原理

新型的电流传感器探头结构如图1所示。该电流传感器包括两个完全相同的环形磁芯C1和C2,磁芯的材料选用铁基纳米晶,磁导率高且容易饱和。Wp、Wf和We分别表示原边绕组、反馈绕组和激励绕组。原边绕组WP穿过磁环中心轴;激励绕组We在C1和C2之间均匀的交叉缠绕;反馈绕组Wf均匀缠绕在两个环形磁芯C1和C2上。Np(通常为1)、Nf和Ne分别代表它们的匝数。原边电流Ip在磁芯C1和C2中产生的总磁通为Φp;反馈补偿电流If在磁芯C1和C2中产生的总磁通为Φf;激励电流Ie在磁芯C1和C2中分别产生大小相等方向相反的磁通Φe1和Φe2。

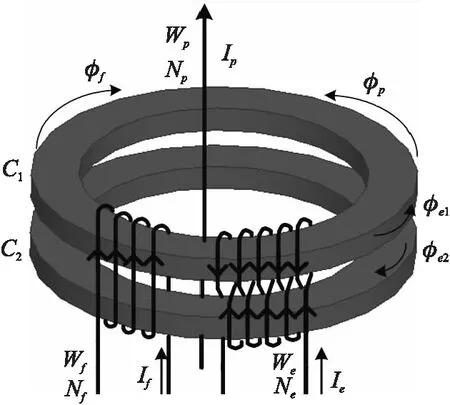
图1 磁芯和绕组的结构

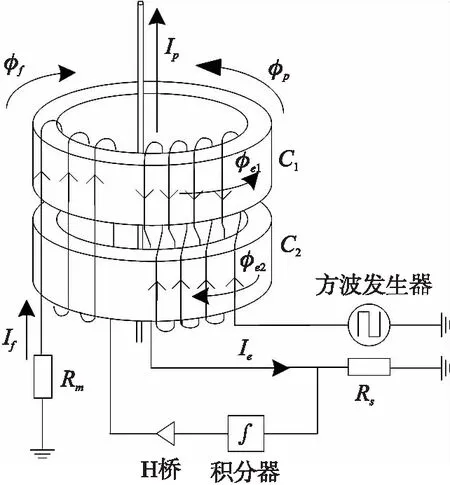
图2 电流传感器的工作原理

新型电流传感器采用闭环零磁通原理。当该电流传感器工作时,高导磁率的磁芯C1和C2在交变激励下往复磁化,呈现周期性饱和与不饱和状态。传感器的工作过程如图2所示。

新型电流传感器工作过程概括如下:方波发生器产生的方波激励电压加载到激励绕组上,同时激励绕组和采样电阻Rs串联。当不存在外部磁场,即原边被测电流Ip=0时,采样电阻Rs上的波形是正负对称的;当存在外部磁场,即原边被测电流Ip≠0时,Ip产生的磁场使磁芯在前、后半周期内不同时达到饱和,使得采样电阻Rs上的波形在整个周期内正负半波不再对称。该采样电阻上的电流经过积分器,输出一个非零的信号,非零信号经过H桥驱动电路,输出反馈电流If到二次反馈绕组上。反馈电流在磁芯中感应出的磁通和被测电流在磁芯中感应出的磁通方向相反。调整二次反馈电流If,直到If产生的磁通Φf和Ip产生的磁通Φp大小相等,方向相反,二次反馈电流不再增大,整个系统达到零磁通状态。二次反馈绕组同时和检测电阻Rm串联,当达到零磁通的状态即满足Φp+Φf=0时,被测电流和反馈电流存在比例关系Ip=-Nf*If/Np。

对于传统的磁通门电流传感器,方波电压加载到激励绕组上并且使磁芯交替处于饱和与不饱和状态。但是互感器效应会在传感器的绕组之间产生,也就是说,激励绕组产生的磁场能够耦合到反馈绕组和原边绕组上。

如图1所示,在本文提出的新型的绕组结构中,激励电流Ie在磁芯C1和C2中分别产生大小相等方向相反的磁通Φe1和Φe2,激励电流耦合到反馈绕组和原边绕组上的磁通为零;在激励绕组和反馈绕组之间、激励绕组和原边绕组之间的互感器效应降低。此外,磁芯C2对外界磁场干扰起到屏蔽的效果。

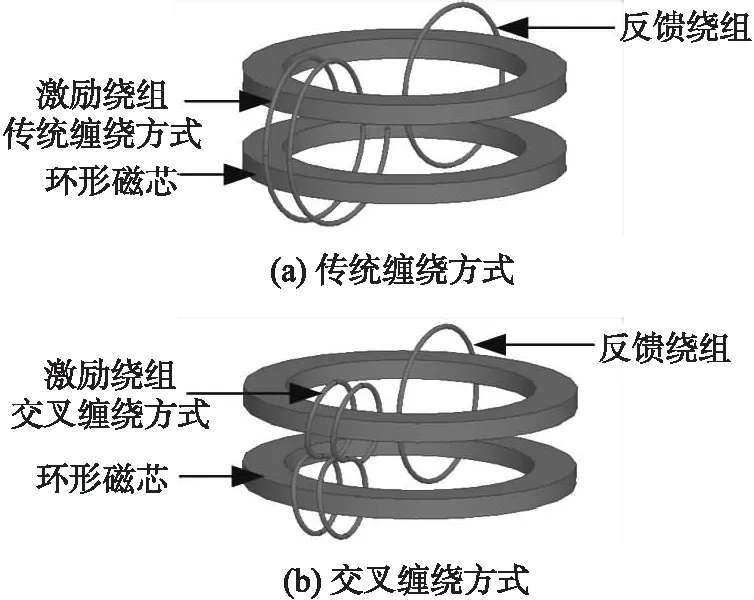
图3 激励绕组的两种结构

2 交叉绕组结构的分析

为了分析激励绕组不同缠绕结构的影响,采用有限元法对两种不同的缠绕方式进行仿真,对于复杂的传感器来再说,定量的分析激励源耦合到反馈绕组和原边绕组的噪声比较困难。为了验证本文提出的缠绕结构的效果,一个简化的三维模型是被建立的,模型如图3所示。

激励绕组和反馈绕组各为2匝和1匝。仿真分析中,激励电流幅值为1.5 A,频率为1 kHz。

以反馈绕组的横截面为观察面,横截面上感应出的电流密度分布如图4所示,经过计算,具有传统缠绕结构的传感器的反馈绕组感应出的电流大约为5.63 mA;具有交叉缠绕结构的传感器的反馈绕组感应出的电流大约为0.78 mA。仿真结果表明,激励绕组采用本文提出的交叉缠绕方式,可以极大减少激励绕组对反馈绕组的耦合影响;同理也能减小激励绕组对原边绕组的耦合影响,降低传感器的噪声,有利于提高传感器的分辨率和测量精度。

图4 反馈绕组电流密度分布

3 仿真与实验

基于理论和仿真的分析,设计制作了实验样机。工作在磁通门原理下的磁芯要求磁导率高,通过理论分析和仿真实验,磁通门检测原理的磁芯选用德国VAC公司的纳米晶磁芯“T60006-L2045-V102”。磁滞损耗小,饱和磁感应强度为1.2 T,磁芯的平均磁路长度和磁芯的横截面积分别为11.8 cm和0.855 cm2,内径为30 mm、外径为45 mm和高为15 mm。所用环形磁芯的B-H曲线如图5所示。

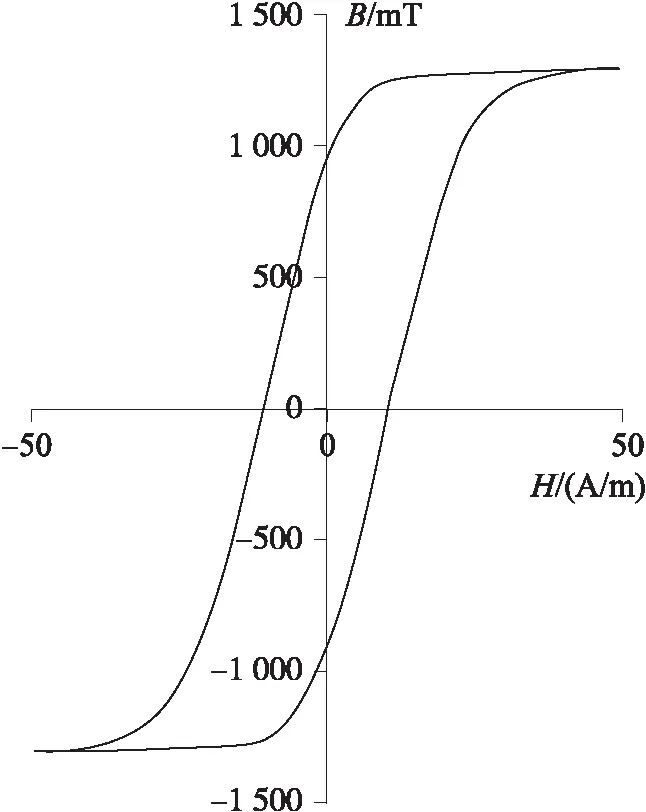
图5 磁芯的B-H曲线

采用的方波激励电压幅值为12 V,频率为1 kHz,通过仿真分析不同被测电流情况下的激励电流波形。当被测电流Ip=0 A时,采样电阻Rs上的电压波形如图6(a)所示;当被测电流Ip非零的时候,仿真结果显示采样电阻上的电压波形在一个周期是不对称的。作为一个例子,当Ip=5 A时,采样电阻上的电压波形如图6(b)所示。对比图6(a)和图6(b),可以看出,被测电流对激励电压有影响:①当被测电流为零的时候电阻Rs上的电压的波形是对称的,也就是说激励绕组上的电流经过积分后为零。②当被测电流非零的时候,电阻Rs上的电压的波形是不对称的,也就是说激励绕组上的电流积分后不是零,激励绕组电压波形取决于被测电流的数值和方向。

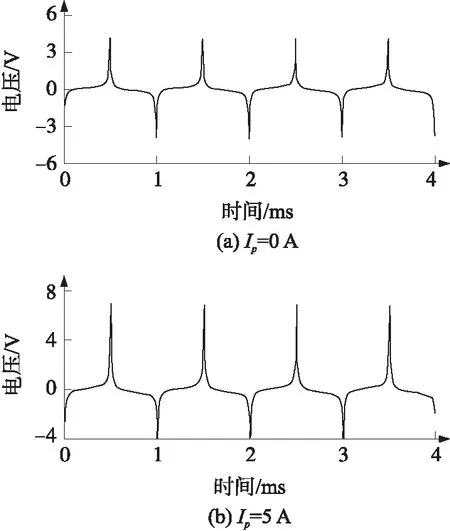
图6 采样电阻电压波形

实验设备包含功率分析仪PA3000、电流探头CT-200-5和电压探头P6139B与本文所设计的传感器样机。①当原边被测电流Ip=0 A时,采样电阻上的电压波形如图7(a)所示;②当原边被测电流Ip=5 A时,采样电阻上的电压波形如图7(b)所示。将实验结果图7(a)、图7(b)和仿真结果图6(a)、图6(b)进行对比,可以看出实验结果和仿真结果具有很好的一致性。

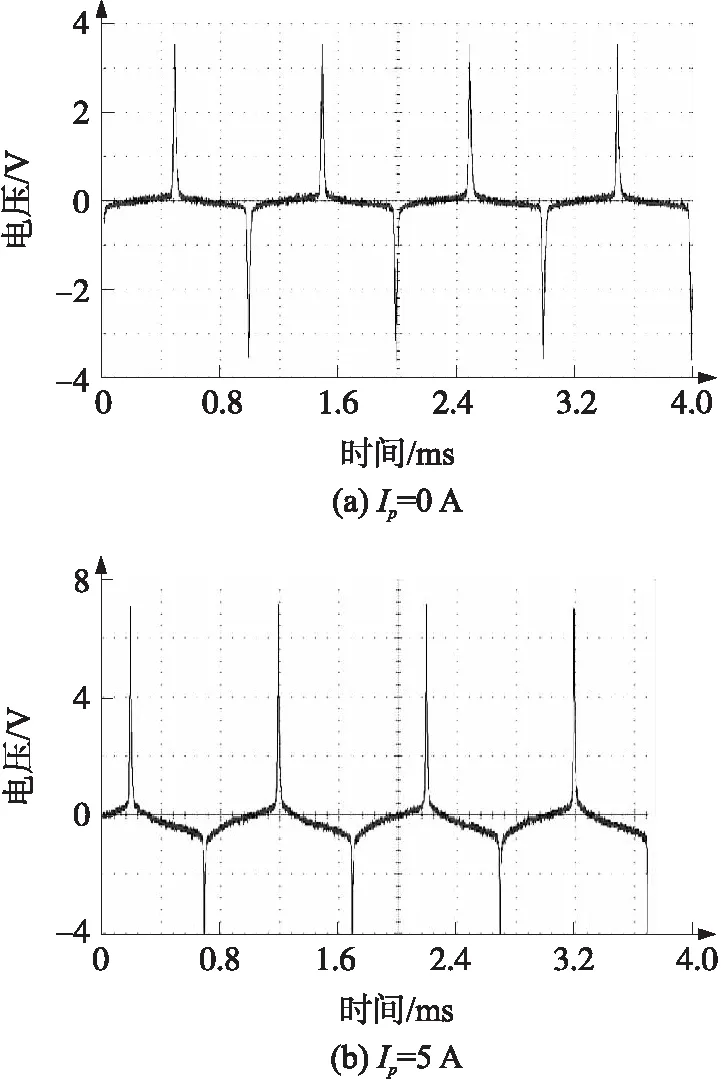
图7 采样电阻电压波形

将具有传统缠绕结构激励绕组的电流传感器与具有交叉缠绕结构激励绕组的电流传感器进行对比实验,被测直流变化范围0～30 A。实验结果如图8所示,测试结果表明:交叉结构能够提高传感器输出的灵敏度。

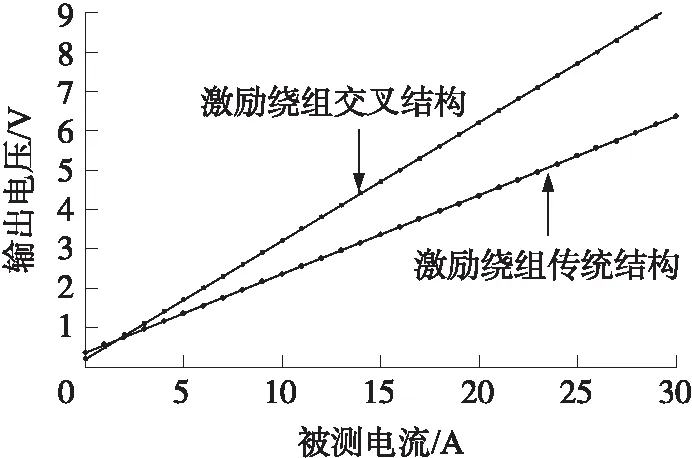
图8 传感器输入输出特性曲线

磁滞效应会影响电流传感器的测量精度,为了分析磁滞现象对电流传感器的影响,本文进行了4组实验:

实验1:激励绕组为交叉缠绕结构,测试电流从0到30 A变化。

实验2:激励绕组为交叉缠绕结构,测试电流从30 A到0变化。

实验3:激励绕组为传统缠绕结构,测试电流从0到30 A变化。

实验4:激励绕组为传统缠绕结构,测试电流从30 A 到0变化。测试结果如图9所示,测试结果表明,采用交叉缠绕结构也能减少磁滞效应带来的误差。

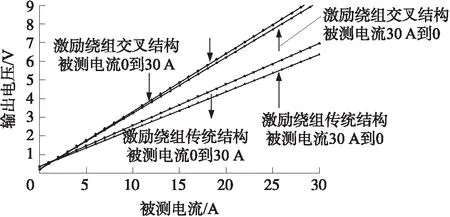
图9 磁滞现象对传感器影响

对本文设计的交叉结构激励绕组的电流传感器在0～30 A进行测试,可以得到测量结果的相对误差曲线,如图10所示。可以看出,电流测量的相对误差在0.4%以下。

图10 新型电流传感器的相对误差

4 结论

激励绕组采用交叉缠绕结构可以极大减少激励绕组对反馈绕组与原边绕组的耦合影响,该结构也能降低磁滞效应带来的误差,有利于降低传感器的噪声和提高传感器的分辨率和测量精度。

[1] Velasco-Quesada G,Roman-Lumbreras M,Conesa-Roca A,et al. Design of a Low-Consumption Fluxgate Transducer for High-Current Measurement Applications[J]. IEEE Sensors Journal,2011,11(2):280-287.

[2] Ripka P,Draxler K,Styblikova R. Measurement of DC Currents in the Power Grid by Current Transformer[J]. IEEE Transactions on Magnetics,2013,49(1):73-76.

[3] 刘杰,康明超,田明,等. FBG电流互感器非线性校正系统研究[J]. 光电子·激光,2017,28(2):155-160.

[4] 玉梅,孙登峰,李平,等. 自全式无线霍尔电流传感器[J]. 仪器仪表学报,2014,35(8):1700-1706.

[5] 谢潇磊,刘亚东,刘宗杰,等. 高频差分绕线PCB罗氏线圈设计[J]. 仪器仪表学报,2015,36(4):886-894.

[6] Yang X,Xie C,Wang Y,et al. Optimization Design of a Giant Magneto Resistive Effect Based Current Sensor with a Magnetic Shielding[J]. IEEE Transactions on Applied Superconductivity,2014,24(3):1-4.

[7] 吕辉,李随源. 低功耗微型磁通门的制备与分析[J]. 传感技术学报,2016,29(1):21-25.

[8] 杨理践,涂传宾,高松巍. 基于磁通门传感器的弱磁场检测方法[J]. 仪表技术与传感器,2014(9):84-87.

[9] Weiss E,Grosz A,Amrusi S,et al. Orthogonal Fluxgate Employing Digital Selective Bandpass Sampling[J]. IEEE Transactions on Magnetics,2012,48(11):4089-4091.

[10] Frydrych P,Szewczyk R,Salach J,et al. Two-Axis,Miniature Fluxgate Sensors[J]. IEEE Transactions on Magnetics,2012,48(4):1485-1488.

[11] 庞娜,程德福,王言章,等. 时间差型磁通门敏感单元巴克豪森噪声处理研究[J]. 仪器仪表学报,2015,36(11):2594-2601.

[12] Wang N,Zhang Z,Li Z,et al. Self-Oscillating Fluxgate-Based Quasi-Digital Sensor for DC High-Current Measurement[J]. IEEE Transactions on Instrumentation and Measurement,2015,64(12):3555-3563.

[13] Isolated Current,Voltage Transducers:Characteristics-Applications-Calculations(3rd Edition),LEM Components,CH 24101 E/US,2004.

[14] Sonoda T,Ueda R,Koga K. An AC and DC Current Sensor of High Accuracy[J]. IEEE Transactions on Industry Applications,1992,28(5):1087-1094.

[15] Li X P,Fan J,Ding J,et al. A Design of Orthogonal Fluxgate Sensor[J]. Journal of Applied Physics,2006,99(8):08B313.

[16] Yang X,Li Y,Guo W,et al. A New Compact Fluxgate Current Sensor for AC and DC Application[J]. IEEE Transactions on Magnetics,2014,50(11):1-4.

[17] Yang X,Guo W,Li C,et al. Design Optimization of a Fluxgate Current Sensor With Low Interference[J]. IEEE Transactions on Applied Superconductivity,2016,26(4):1-5.

[18] Yang X,Guo W,Li C,et al. A Fluxgate Current Sensor with a U-Shaped Magnetic Gathering Shell[J]. IEEE Transactions on Magnetics,2015,51(11):1-4.