基于平面阵列电磁传感器的金属缺陷检测新方法*
2018-02-05汪剑鸣杨伟明崔莉莎孙玉宽王化祥窦汝振
汪剑鸣,杨伟明,王 琦*,崔莉莎,孙玉宽,王化祥,窦汝振
(1.天津工业大学电子与信息工程学院,天津 300387;2.天津市光电检测技术与系统重点实验室,天津 300387;3.天津大学电气与自动化工程学院,天津 300072;4.中国汽车技术研究中心,天津 300300)
随着我国工业快速发展,大量不同种类和规格的金属材料被广泛应用。在金属材料的使用过程中,必然存在着金属缺陷问题。金属缺陷检测中最常见也很有效的一种方法是无损检测,在不破坏金属材料结构的前提下能为检测者提供有价值的检测信息,整个检测过程有效降低了检测成本[1]。在传统金属缺陷无损检测设备中一般为单个或双传感器[2],在检测时需移动传感器或被测金属板,检测用时较长且需要相应的机械装置辅助检测,容易造成检测误差,影响检测结果,不能满足检测现场的实时检测需求。通过增加传感器数目实现了多传感器检测,检测精度得到提高。多传感器检测时一般采用特征提取法对测量结果进行分析,但多数仅能对缺陷位置、形状和尺寸信息中的一个或两个参量进行检测,检测结果较抽象。如果在检测时能得到金属缺陷分布图像,检测结果就更加直观形象。本文介绍的电磁层析成像技术EMT(Electromagnetic Tomography)正是一种基于电磁原理的可视化无损检测技术,通过平面阵列电磁传感器获取被测物场信息,再利用图像重建算法重建被测物场内电导率或磁导率的分布情况。EMT技术在无损检测应用中具有检测速度快、灵敏度高、无接触和检测可视化的优点,同时EMT检测系统成本较低,在航空、冶金、石油等行业领域有着广阔应用前景[3-4]。
在金属缺陷检测时,传统检测方法通过特征提取能够对缺陷位置、形状和尺寸3个参数中的一到两个进行检测,但检测可视化程度较低,缺陷成像结果直观性差[5]。本文中基于新型平面阵列电磁传感器的EMT检测方法可实现对3个参数的同时检测,检测结果以图像形式显示,直观反映出金属表面缺陷的位置、形状和尺寸。由于金属缺陷呈稀疏分布,EMT检测方法在重建金属缺陷图像时采用了稀疏加权算法。本文从仿真和实验角度验证了EMT检测方法在重建金属缺陷图像方面的优越性。
1 基于EMT的缺陷检测系统
1.1 EMT系统传感器设计
传感器是整个EMT检测系统的重要部分。本文为实现对平面金属缺陷的可视化检测,设计了如图1所示的平面传感器。传感器由9个线圈组成,线圈呈3×3矩阵排列,并固定在一个非导磁塑料正方形盘上。各线圈由线径0.3 mm铜线绕制而成,匝数为100匝,高10 mm,内径15 mm,外径17 mm。

图1 传感器部分
与其他传感器相比,本文中传感器具有以下优点:首先,该平面阵列电磁传感器线圈呈矩阵排列,能有效解决中心区域检测不敏感问题,均匀分布的阵列线圈也提高了传感器在不同区域测量时的一致性。其次,线圈数量增加,能得到更多测量数据,成像效果更好。最后,传感器通用性更强,适用于各种平面金属缺陷检测。
检测时激励测量策略是先向一个线圈中输入激励电流,再依次测量非激励线圈上的感应电压值。之后按次序将下一个线圈作为激励线圈通入电流,再分别测量其他非激励线圈的感应电压值,重复该过程直到所有线圈都依次充当过激励线圈。
1.2 基于平面式阵列电磁传感器的EMT检测系统
整个基于平面式阵列电磁传感器的EMT检测系统由五部分构成,包括传感器部分、信号源模块、多路选通模块、高速采集模块和上位机,整个系统的结构示意图如图2所示。EMT检测系统的工作原理为在电磁感应作用下,利用电磁传感器对敏感场进行循环激励,检测被测区域内导电物体相互作用形成的物场,获取被测对象的边界电压信息,再利用图像重建算法再现物场内部的分布情况。实际的实验系统如图3所示,信号源模块产生特定幅值频率的正弦激励信号,接着通过串口控制的多路选通模块施将激励信号施加到相应的激励线圈上,利用多路选通模块控制相应检测线圈得到感应电压,再通过数据采集模块采集相应检测线圈电压并传送至上位机,最后利用图像重建算法进行金属缺陷图像重建。
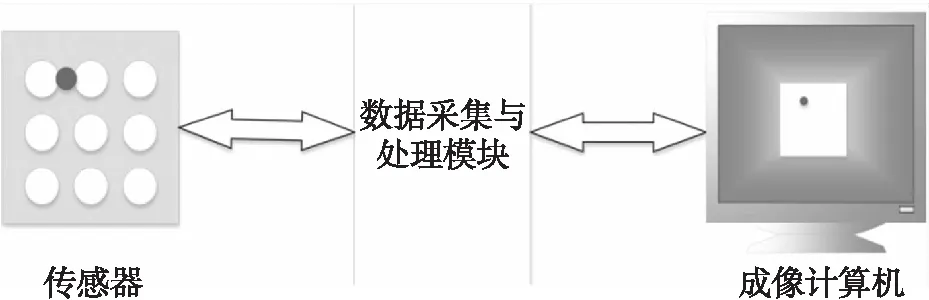
图2 平面式传感器EMT检测系统结构图

图3 实验用平面式传感器EMT检测系统图
2 金属缺陷检测方法
本文提出了一种基于平面阵列电磁传感器的EMT检测新方法,该方法在重建缺陷图像时用到了稀疏加权算法。与传统扫描式检测方法相比,新方法实现了金属缺陷的可视化检测,成像结果较好反映出缺陷的位置、形状和尺寸。
2.1 基于平面阵列电磁传感器扫描式检测方法
传统扫描式检测方法中,首先利用传感器分别对标准铝板和有缺陷铝板表面进行检测。传感器检测结束后,对检测数据进行处理,得到每个线圈以平均值形式表示的检测结果。检测结果作为图像重建的原始数据,利用成像算法重建图像,从而判断出缺陷所在位置,具体方法如下。
传统扫描式检测方法按照2.1节中的激励测量策略得到的检测数据可表示为一个9×9的矩阵,即
该矩阵中每个元素可以表示为xij,其中i=1,…,9,j=1,…,9,且i≠j,i的值表示相应激励线圈,j的值表示相应检测线圈。用xij表示对标准铝板表面检测时第i号线圈为激励时第j号线圈的检测值。
则j号线圈对标准铝板表面的检测结果为
(1)
同理可得j号线圈对有缺陷铝板表面的检测结果为τ
l2,i=1,…,9;j=1,…,9
(2)
将j号线圈两次检测结果差值j作为最终检测结果,如式(3)所示。其中σ0表示对有缺陷铝板表面检测时第i号线圈作为激励第j号线圈的检测值。
(3)
可依次得到9个线圈的最终检测结果,将得到的检测结果表示为3×3矩阵形式,即
为便于与EMT检测方法的成像结果进行比较,将传统扫描式检测方法的检测结果表示为图像形式。矩阵ΔA中每一个元素对应一个像素块,像素块位置与测量线圈位置相对应。
2.2 基于平面阵列电磁传感器EMT成像检测方法
2.2.1 成像数学模型
基于平面阵列电磁传感器EMT检测方法的数学模型如式(4)所示[6]:
v=F(σ)
(4)
式中:σ代表电导率分布,v∈RM代表传感器线圈检测到的感应电压值,F是由正问题决定的非线性函数[7],若F和σ已知,便可计算电压v。可用式(4)截断的泰勒展开式来描述,如式(5)所示。
(5)

v-F(σ)=S(σ-σ0)
(6)
B=SG
(7)
式中:B代表电导率变化引起的电压变化量,G代表电导率分布的像素点。
成像过程是在已知系统的磁场激励特性、传感器边界条件和检测信号的情况下,通过特定的图像重建算法得到被测物场中电导率和磁导率的空间分布图像。
2.2.2 灵敏度矩阵构建
在进行缺陷图像重建时,灵敏度矩阵构建是其中关键技术之一。灵敏度矩阵是电磁传感器的敏感场分布数据,是电磁层析成像数学模型构建与求解的先决条件。求解灵敏度矩阵通常用到的方法有测量扰动法、模型扰动法、解析法和实际测量法[8]。本文中采用解析法,灵敏度矩阵的解析法计算已被完整推导出,假设线圈i为激励线圈,线圈j为检测线圈时,计算公式如式(8)所示。
(8)
公式中S为灵敏度,Δk=Δσ+jwΔε为复电导率变化,ΔZ为互阻抗变化,Ii、Ij分别是线圈i和线圈j中的激励电流和感应电流,Ei、Ej是通过有限元计算得到的不同激励条件下被测物场的感应电场分布。其他不同线圈间的灵敏度分布计算与此类似,可由此得到整个灵敏度矩阵[8-9]。
2.2.3 稀疏加权算法
检测新方法中EMT图像重建是根据测量数据和灵敏度矩阵来求电导率分布,即可转化为求解方程(7)的过程。由于图像重建问题中存在的病态性,同时灵敏度矩阵S既非方阵又非满秩,不能对式(7)直接求逆。一般采用的解决方法是引入如式(9)所示的正则项构造,并求满足式(9)的最优解。
(9)

(10)
式中:l1范数惩罚项的惩罚作用对解中的所有元素同样适用,对非平滑图像的重建效果很明显,能有效削弱重建图像的平滑过渡,很好地检测重建图像的边缘和突变。与l2正则化方法相比较,l1正则化方法能有效保持重建图像的边缘性[12],更适合缺陷图像重建。
由于存在一阶范数,不能够直接对式(10)进行求导,在处理不可导项时存在一系列稀疏加权算法,本文中采用的是成像效果较好、收敛速度较快的SplitBregman算法(SB算法)。
根据SplitBregman算法[13],电导率分布可按照以下3个步骤来进行迭代求解。
步骤1:
(11)
步骤2:
(12)
步骤3:
bk+1=bk+Gk+1-dk+1
(13)
式中:G的初始值设为0,β是惩罚系数,为正值,b和d作为辅助变量,初始值设为0。式(11)为二阶范数优化问题,通过求导可得
(14)
式(12)为l1正则问题,d可通过向量值算子进行求解
dk+1=Shrink(LGk+1+bk,a/β)
(15)
向量值Shrink算子如下:

(16)
式中:x为一向量,τ为一常数。
3 仿真结果及分析
为对比两种检测方法在金属缺陷检测时的缺陷图像重建效果,本文进行了相关仿真实验,设计了如图4所示的传感器仿真模型。模型由9个铜质材料线圈按照33矩阵形式排列而成,传感器仿真模型中线圈参数与2.1节中真实线圈的参数设置相一致,且线圈到铝板的距离是2 mm。在对金属缺陷检测时,将传感器置于缺陷上方。每个线圈既可当做激励线圈,也可当做检测线圈。当其中一个线圈作为激励线圈时,其余8个线圈当做检测线圈,经过循环激励测量,得到89个检测数据。

图4 EMT系统传感器仿真模型
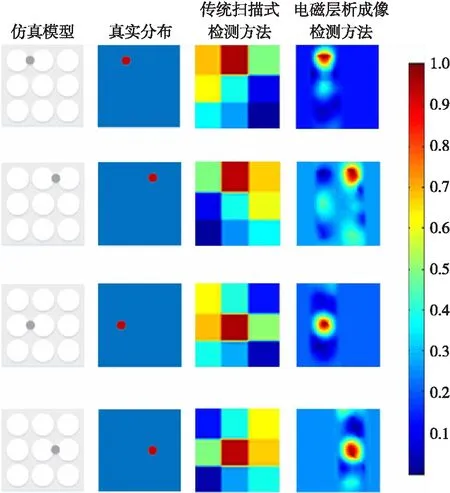
图5 不同位置处一个缺陷重建结果
通过仿真实验得到检测数据后,分别使用传统扫描式检测方法和EMT检测方法得到缺陷重建图像,缺陷具体位置、形状和尺寸如图5所示。图5中第1列代表仿真模型,深灰色小圆代表缺陷,外边的浅灰色正方形代表铝板,缺陷半径为3.5 mm,深度为5 mm。第2列为介电常数真实分布,第3列为传统扫描式检测方法的成像结果,第4列为EMT检测方法的成像结果。仿真实验中,首先建立与有缺陷铝板形状、厚度相同的无缺陷铝板仿真模型,进行正问题仿真,得到不同激励线条件下被测物场的感应电场分布,以及检测线圈中的感应电流值和感应电压值,结合已知的激励电流值,由式(8)计算获得重建图像所需的灵敏度矩阵。
为对两种检测方法的缺陷图像重建结果进行定量比较,引入了重建图像相对误差概念,如式(17)所示:
(17)
式中:G为重建电导率分布,G*为原始电导率分布。
两种检测方法对于一个金属缺陷的重建图像相对误差计算结果如图6所示。

图6 两种检测方法对一个缺陷重建图像的相对误差
从图5可看出,采用传统扫描式检测方法的图像重建结果中有9个区域,每个区域颜色不同。在检测时逐渐移动传感器使缺陷处于传感器下方,重建图像中对应有缺陷处的颜色值最大,能反映出缺陷所在区域,符合检测的预期结果。但不足之处在于重建图像并不能准确反映缺陷位置、形状和尺寸,即缺陷检测的精确度不够。而采用EMT检测方法的重建图像结果能较好反映出缺陷位置,成像较清晰,能基本判定缺陷形状和尺寸。同时,从图6可以看出EMT检测方法重建图像的相对误差比传统扫描式检测方法重建图像的相对误差低很多,可知EMT检测方法中缺陷图像重建效果更好。
以上研究了检测单个金属缺陷时的图像重建结果,为进一步证明EMT检测方法在金属缺陷图像重建方面的优势,又对有两个缺陷的铝板进行了仿真检测和缺陷图像重建,重建结果如图7所示。
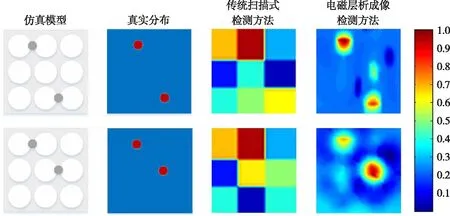
图7 不同位置处两个缺陷重建结果
图7中第1列代表仿真模型,缺陷半径为3.5 mm,深度为5 mm。从图7可以看出,传统扫描式检测方法的成像结果只能反映出金属缺陷所在大致区域,无法判定缺陷的形状尺寸。而EMT检测方法的成像结果能较好反映物场信息分布,仿真实验中采用的稀疏加权算法实现了对金属缺陷位置、形状及尺寸的较好重建,成像效果良好。对比可看出EMT检测方法中缺陷重建图像质量较高。
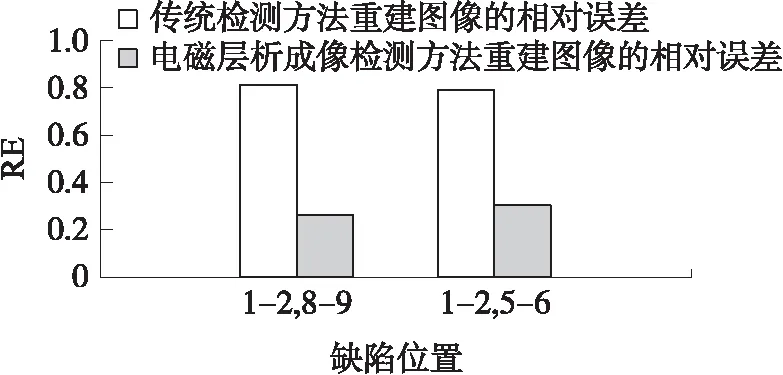
图8 两种检测方法对两个缺陷重建图像的相对误差
图8为两种检测方法中对两个金属缺陷铝板检测时重建缺陷图像的相对误差。
从图8可以看出,在多个缺陷图像重建时,EMT检测方法重建图像的相对误差要明显比传统扫描式检测方法重建图像的相对误差低。由此证明EMT检测方法在多缺陷检测时也有优势。
4 实验验证及分析
为进一步验证基于平面式阵列电磁传感器的EMT检测方法在金属缺陷图像重建中的实际效果,本文对真实有缺陷方形铝板进行了缺陷检测实验。待检测铝板如图9所示,铝板长宽均为12 cm,厚度为1 cm。其中图9(a)为无缺陷铝板,作为实验空场采集对象;图9(b)为有一个缺陷铝板;图9(c)为有两个缺陷铝板;缺陷半径为3.5 mm,深度为5 mm。实验所用的传感器及其线圈设计参数在2.1节中已介绍。实验中首先得到与图9(a)无缺陷铝板形状厚度及电导率一致的仿真模型,进行正问题仿真,得到不同激励条件下被测物场的感应电场分布,以及检测线圈中的感应电流值和感应电压值,结合已知的激励电流值,由式(8)计算获得重建图像所需的灵敏度矩阵。实验时将传感器在整个铝板区域内扫描检测,为比较两种检测方法的检测效果,将传感器经过金属缺陷时的检测成像结果进行了对比分析。

图9 实际实验中待测铝板
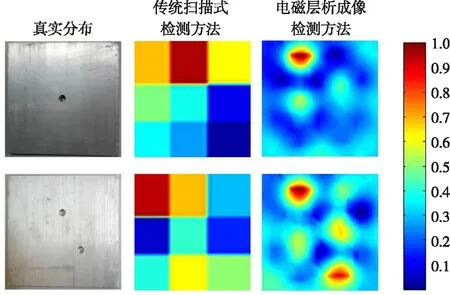
图10 真实实验数据缺陷重建结果
实验中分别采用传统扫描式检测方法和EMT检测方法进行了金属缺陷检测,缺陷图像重建结果如图10所示。
图10中第1列为有缺陷铝板,缺陷半径都为3.5 mm,深度为5 mm。第2列和第3列分别为传统扫描式检测方法和EMT检测方法的缺陷图像重建结果。从图10可看出EMT检测方法的成像结果能够很好反映出金属缺陷位置、形状和尺寸,且成像较清晰。而传统扫描式检测方法的成像结果只反映出缺陷所在区域,不能准确定位,更无法判定缺陷形状和尺寸。
对比真实实验与仿真实验的缺陷重建结果,由于真实实验环境复杂,受干扰较多,成像质量较差,但重建结果基本一致。说明基于平面式阵列电磁传感器的EMT检测方法能够有效应用于金属缺陷检测中。
5 结论
本文为解决传统扫描式金属缺陷检测方法中缺陷位置、形状和尺寸测量失真的问题,提出了针对金属缺陷的EMT检测新方法。采用新型平面阵列电磁传感器,能有效解决中心区域检测不敏感问题,增强不同区域测量一致性,提高检测精度,可实现对最小直径为3 mm,深度为5 mm的金属缺陷可视化检测。基于SplitBregman算法,实现了金属缺陷成像。仿真和实验的金属缺陷可视化检测结果表明,与传统扫描式检测方法的金属缺陷图像重建结果相比,新方法的缺陷成像结果更加形象直观,有效提高了对金属缺陷位置、形状和尺寸检测的准确性。下一步研究中将继续改进传感器线圈参数与激励检测方式,由串行检测改为并行检测,提高系统检测速度和精度;同时进一步优化图像重建算法,提高缺陷成像质量与速度。
[1] 杨海龙. 多层板材电磁无损检测技术研究[D]. 电子科技大学,2015.
[2] 张思全,唐江锋. 一种新型相移场探头改变导体涡电流分布的理论验证[J]. 传感技术学报,2016,29(8):1169-1175.
[3] 张闯,刘素贞,金亮,等. 用于金属管材裂纹检测的涡流加载线圈设计[J]. 电工技术学报,2013,28(2增):172-175.
[4] 徐凯,陈广,尹武良,等. 基于场量提取法的电磁层析成像系统的灵敏度推算[J]. 传感技术学报,2011,24(4):543-547.
[5] 何敏,柴孟阳. 三种电磁无损检测方法综述[J]. 测控技术,2012,31(3):1-4.
[6] 熊汉亮,徐苓安. 电磁层析成像(EMT):正问题的理论分析[J]. 应用数学和力学,2000,21(9):933-941.
[7] Wang Q,Wang H X,Zhang R H,et al. Image Reconstruction Based onl1Regularization and Projection Methods for Electrical Impedance Tomography[J]. Review of Scientific Instruments,2012,83(10):104707-104711.
[8] 尹武良. 低频电磁传感检测技术[M]. 北京:科学出版社,2010:82-84.
[9] Yin W L,Peyton A J,Stefani F,et al. Theoretical and Numerical Approaches to the Forward Problem and Sensitivity Calculation of a Novel Contactless Inductive Flow Tomography(CIFT)[J]. Measurement Science and Technology,2009,20(10):105503-105509.
[10] Shi J,Liu F,Zhang G,et al. Enhanced Spatial Resolution in Fluorescence Molecular Tomography Using Restarted L1-Regularized Nonlinear Conjugate Gradient Algorithm[J]. Journal of Biomedical Optics,2014,19(4):046018-046018.
[11] Koh K,Kim S J,Boyd S. An Interior-Point Method for Large-Scalel1-Regularized Logistic Regression[J]. Journal of Machine Learning Research,2007,8(Jul):1519-1555.
[12] Lingala S G,Hu Y,Di Bella E,et al. Accelerated Dynamic MRI Exploiting Sparsity and Low-Rank Structure:Kt SLR[J]. IEEE Transactions on Medical Imaging,2011,30(5):1042-1054.
[13] 李昊庭,徐灿华,刘本源,等. 稀疏加权算法与GREIT算法在颅脑电阻抗成像中的对比研究[J]. 中国医疗设备,2016,31(11):23-27.
