基于双眼同步运动特征约束的Kalman瞳孔跟踪算法*

张远辉,李 颜,李孝禄,朱俊江

(中国计量大学机电工程学院,杭州 310018)

人眼是人机交互过程中自然而快捷的通道,计算机屏幕上的注视点定位是实现人机信息交互的主要手段。红外光环境下的瞳孔跟踪作为注视点定位中的关键技术,在心理学、医学、军事、商业界面评估与设计方面都有极大前景与研究价值,数十年来受到学界的广泛关注。

然而瞳孔的运动过程总是伴随着各种各样的噪声,一些噪声来源于外部环境:外部的光线干扰、毛发遮挡,令瞳孔目标的时序定位存在误差;一些噪声来源于眼睛运动本身:眼部的抖动,眨眼等无意识动作[1]。这些噪声使得瞳孔跟踪在快速性和鲁棒性上存在一定的难度,无法满足人机交互中对注视点准确性和实时性的要求。

近年来视觉跟踪领域取得的一些成果有:李兵等人提出的基于人工神经网络进行瞳孔视觉跟踪的研究[2],只需商业摄像头就能在普通实验室光照条件下达到识别精度高于88%的视线跟踪,而文章仅进行了静态注视映射的训练,尚未考虑运动状态下的视线跟踪。瞳孔运动状态下的跟踪技术大都依赖于接触式的眼部图像获取设备,包括Chang等人提出的通过穿戴式的双目摄像头拍摄瞳孔运动情况从而估计3D环境下的视线方向[3];张琴等人提出的通过安装在眼镜上的摄像头采集瞳孔运动图像,利用硬件电路分离信号传送信息[4];杨庆华等人提出的眼动跟踪方法同样采用可穿戴式的系统硬件方案[5],在普通眼镜上安装CCD摄像头;邹云海等人提出的快速投影跟踪算法[6],能够实现高速眼动跟踪,但其算法对硬件要求较高,需依赖FPGA完成。也有一些研究人员依赖非接触式的眼部图像获取设备进行视线跟踪研究,例如Zanetti等人利用Kinect设备降低3D场景中基于瞳孔-角膜反射的视线跟踪误差,提高红外光照射下对受试者眼部特征跟踪的准确度[7]。

Kalman滤波器在针对运动目标的检测领域运用甚广[8-9]。例如王江等人提出的基于Kalman滤波的双目视觉跟踪[10],针对场景中的目标图像有良好的跟踪效果;王丽等人提出的综合运用Kalman滤波器的眼部跟踪算法[11],对于跟踪人脸中的眼部图像有较强的鲁棒性,但并未精确至瞳孔坐标;Jiannan Chi等人提出的将粒子滤波和Kalman滤波结合进行瞳孔跟踪的算法[12],相较于其他结合算法定位精度上有所提升但算法流程相对繁琐。由于眼部瞳孔运动相较于人脸中眼部跟踪或者驾驶环境存在更多噪声干扰且需要的跟踪精度更高,将Kalman滤波器算法运用在瞳孔运动跟踪检测领域的改进研究成果相对来说较少。

图2 红外光照射下眼部图

本文提出一种基于双眼同步运动特征约束的Kalman跟踪算法,算法的核心思想是通过双眼的同步运动特征,简化跟踪系统模型:在对瞳孔位置和速度进行估计的基础上,利用瞳孔的间距矢量参数进行隐式参数估计,为进一步检测人脸与摄像机之间的距离以及识别人脸姿态奠定了基础。通过和滑动平均滤波算法、常速度Kalman滤波算法等的对比实验表明,本算法在抗干扰性能方面和计算量方面均有一定优势。

1 实验平台搭建

1.1 传感硬件平台搭建

在可见光下,人眼的瞳孔和虹膜区域反射情况类似,因此采用可见光照射人眼,并不能从图像中准确提取瞳孔边缘,进而定位瞳孔中心。而在红外光照射下,由于瞳孔区域与虹膜区域对红外光的反射率不同,使得两个区域在红外成像中存在较为明显的差异,有利于瞳孔边缘的定位和识别,因此国际上通行的注视点识别系统中,普遍使用红外光下基于视觉的视线跟踪方法。另外,人眼视觉神经细胞对红外光照射不敏感,因此红外光照射不会引起受试者的眼部不适和视觉干扰。本文搭建的红外光照明下的头戴式注视点传感实验装置,如图1所示。

装置上的右侧摄像头可以通过手拧螺丝进行姿态自锁,调整支架扭转角度后拍摄双眼区域图像,拍摄图像如图1所示。

图1 头戴式注视点传感实验装置

1.2 瞳孔中心定位预处理

瞳孔跟踪和瞳孔定位密不可分,在对运动过程中的瞳孔进行跟踪之前对瞳孔中心位置进行准确定位,获得双眼瞳孔中心的初始坐标用于跟踪算法的输入数据,能够有效提高瞳孔跟踪算法的精度。

图2为红外光照射下的眼部图,采集图像像素大小为1 920 pixel×1 080 pixel。图2(a)为瞳孔中心定位过程示意。首先通过图像分割,从图像中获取眼部子图。从眼部子图中可见瞳孔区域在二维图像中与周围区域的颜色灰度存在较大差异,本文采用结合凸区域投票和模型约束的算法对瞳孔进行定位。首先利用星射线算法[13]提取边缘点,接着利用图像中特征点的位置和梯度信息,进行凸区域投票获取瞳孔近似边界,然后通过椭圆模型约束迭代优化边缘点,从而准确定位瞳孔位置。图2(b)中瞳孔中心红点位置即为由图2(a)眼部子图识别出的瞳孔中心结果。

2 双眼同步运动特征约束下的Kalman瞳孔跟踪算法

2.1 双眼同步运动规律

Kalman滤波器是根据无后性假设和独立性假设这两大基本假设以及贝叶斯估计相关理论得出的状态估计方法[14]。Kalman滤波同时考虑预测模块和更新模块的协方差,赋较大的权重给误差较小的项,赋较小的权重给误差较大的项,达到使预测结果误差最小的目的。考虑使用Kalman滤波器对双眼的运动进行建模,建立眼球运动的过程方程和观测方程。

瞳孔间距矢量如图2(b)所示。把图像的左上角作为原点,水平向右为x轴,竖直向下为y轴,两个瞳孔的坐标可以表示为左眼(xl,yl)和右眼(xr,yr)。实时跟踪两个眼睛的运动状态还需要估计左右眼的瞳孔的速度在xy轴上的分量,即左眼速度(vxl,vyl)与右眼速度(vxr,vyr)。进一步地,为实现人脸姿态的估计,还需要估计瞳孔间距。因此,物理量xl,yl,xr,yr,vxl,vyl,vxr,vyr以及衡量瞳孔间距的两个物理量dw(两瞳孔的水平间距)和dh(两瞳孔的竖直间距),一共10个变量需要估计。用这10个物理量构建状态列向量,应用Kalman滤波算法的计算复杂度为O(n2)(其中n=10),因此计算量较大[15]。

分析上述10个状态变量,发现部分变量和变量之间存在着耦合和约束关系。人眼运动的一个典型特征就是双眼同步运动。假设人的头部位置和姿态保持不变,人眼在向左看和向右看的时候,两个瞳孔同时向左或者向右运动[16]。

2.2 双眼同步运动的Kalman滤波器设计

2.2.1 过程方程的构建

本文滤波算法中将10维状态变量精简为6维状态变量。图 2中红色箭头所示为瞳孔矢量,该矢量由左侧瞳孔中心指向右侧瞳孔中心,把该瞳孔矢量的中点位置,作为系统过程的状态向量,构造的6维的系统过程方程,如式(1)所示。

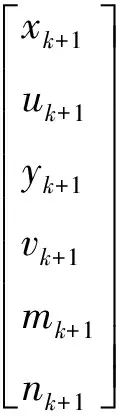
(1)

式中:xk+1和uk+1表示k+1时刻瞳孔矢量中心位置在x轴方向(水平)方向的位置和速度,yk+1和vk+1表示k+1时刻瞳孔矢量中心位置在y轴方向(竖直)方向的位置和速度,mk+1和nk+1表示k+1时刻,瞳孔矢量在x轴和y轴上的投影分量。dt表示连续两次图像采集时刻的时间间隔。wk是k时刻的过程噪声项,它满足高斯分布N(0,Qk),其中Qk表示wk的协方差矩阵,是一个6×6的对角矩阵,即过程方程中状态变量的过程噪声协方差矩阵。

(2)

式中:Q1,Q2,Q3,分别为2×2的协方差矩阵。在忽略干扰的情况下,可以认为双眼在扫视过程中,瞳孔矢量中心位置为匀速运动,如果考虑瞳孔在运动过程中受到各种扰动的影响,可以将过程噪声wk看作眼球在运动过程中受到一个等效扰动Fa的作用力,其产生的等效加速度为a,那么协方差矩阵的取值如下推导所示。

2.2.2 观测方程的构建

由于图像处理中只能检测出左右眼的瞳孔中心坐标,因此系统的观测方程如式(3)所示:

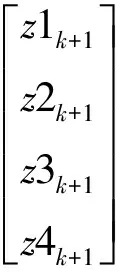
(3)

式中:等号左侧的z1k+1和z2k+1表示左侧瞳孔的测量位置x坐标和y坐标,z3k+1和z4k+1表示右侧瞳孔的x坐标和y坐标。等式中的下标均表示当前为离散时间k时刻的状态值,等式最右侧的vk+1是k+1时刻的测量误差项,该误差项服从高斯分布,具有如下形式N(0,Rk+1),其中Rk+1表示k+1时刻的测量噪声的协方差矩阵,是一个4×4的矩阵。

(4)

式中:Rvar为单侧瞳孔坐标的方差,Rcov为两侧瞳孔坐标的协方差。

3 实验结果和分析

3.1 实验参数设置

3.2 本文算法与常速度Kalman滤波算法仿真实验结果

由于直接构造10维Kalman滤波器的计算量较大,作为和本文提出方法的对比,本文将左右眼的状态变量进行分离,构建两个4维的常速度Kalman滤波器分别对左右眼瞳孔进行状态跟踪,同时亦构造一个2维的Kalman滤波器估计瞳孔间距矢量。左右眼的常速度滤波器采用如下方式构建系统的过程方程和观测方程。

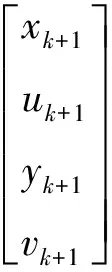
(5)

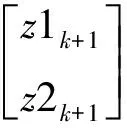
(6)

此处过程方程式(5)和观测方程(6)与之前的式(1)和式(3)在定义形式上是一致的。式(1)的位置坐标和速度是基于瞳孔矢量中心点的,而式(5)和式(6)坐标状态变量和速度状态变量仅仅是某一侧的瞳孔运动状态(例如左眼瞳孔的位置和速度)。在此对比实验中,过程协方差、测量协方差矩阵均采用与本文滤波算法相同的数值。

3.3 仿真实验

模拟双眼瞳孔水平向右匀速扫视动作来构造仿真数据序列,仿真序列数据包括:双眼瞳孔矢量中心的x坐标,双眼瞳孔矢量中心的y坐标,两瞳孔的水平间距dw,两瞳孔的竖直间距dh。单侧瞳孔的坐标由上述4个量计算获得。其中,双眼瞳孔矢量中心的x坐标的真实值设定为起始点为0,速度为10 pixel/s,时间间隔dt=0.1 s的100个离散点的坐标序列,双眼瞳孔矢量中心的y坐标的真实值设定为零。两瞳孔的水平间距dw的真实值设定为100 pixel,两瞳孔的竖直间距dh的真实值设定为40 pixel。上述4个量的测量值均由对应的真实值加上一个均值为零的高斯白噪声所得,并且模拟测量序列中不包含较大干扰。

将模拟测量值分别置入本文算法模型和常速度Kalman滤波算法模型获得估计值,估计值与真实值的几何距离为仿真实验误差。两种算法模型的x轴坐标误差与y轴坐标误差如表1所示,其中本文算法下的x轴坐标误差比常速度Kalman滤波算法减小了11%,y轴坐标误差减小了4.8%。

表1 仿真实验下两种算法模型的估计误差对比

3.4 两种眼部动作下的对比实验结果

3.4.1 本文算法的实验结果及对比

以某次双眼水平扫视动作和自左下至右上扫视屏幕对角线动作中的瞳孔图像为研究对象,实验中的拍摄和图像处理的间隔时间dt为0.1 s,扫视动作持续时间为10 s左右。使用电脑屏幕的分辨率大小为2 560 pixel×1 600 pixel。

根据实验数据给出状态变量矩阵的初值,对应状态向量的协方差P的初始值一般定义比较大的值[14],本文实验中定义如式(7)所示:

P0|0=diag[50 000 50 000 50 000 50 000 50 000 50 000]

(7)

图3是扫视屏幕对角线瞳孔矢量中心位置和瞳孔矢量中心点速度的估计结果,横坐标为时间,单位为秒,纵坐标分别为矢量中心点的像素坐标与速度大小。图3(a)中实线表示滤波器对矢量中心点的坐标估计,点线表示测量的瞳孔中心位置。事实上,因为无法直接测量该位置的坐标,此处是通过左右瞳孔测量位置坐标求平均值的方法得到的。图中在7.5 s时刻,存在由于外部大扰动带来的测量噪声,具体表现为x轴坐标测量位置出现较大偏差,而在该扰动影响下,滤波器的输出抖动幅度不大,约为5 pixel。图3(b)点线为测量结果(测量结果由测量数据对时间的导数计算得到),实线为xy两轴的速度估计结果,可见在7.5 s受到测量扰动后,速度估计曲线并没有大的浮动。扫视对角线动作下x方向的速度为-10 pixel/s左右,y方向的速度为-4.6 pixel/s左右,基本符合本次实验中自左下至右上扫视屏幕对角线的动作过程。

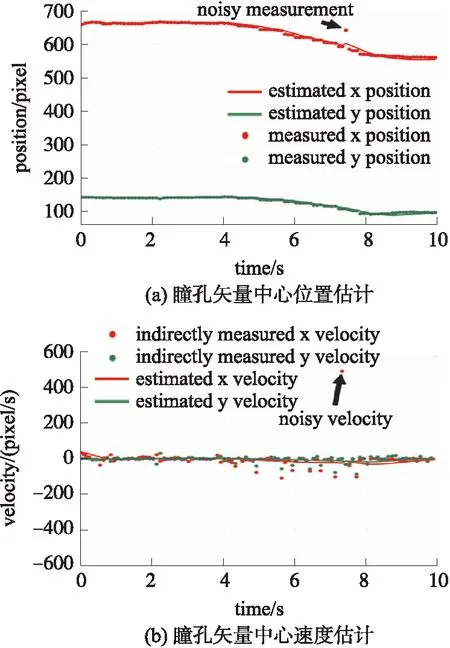
图3 扫视屏幕对角线瞳孔矢量中心估计结果

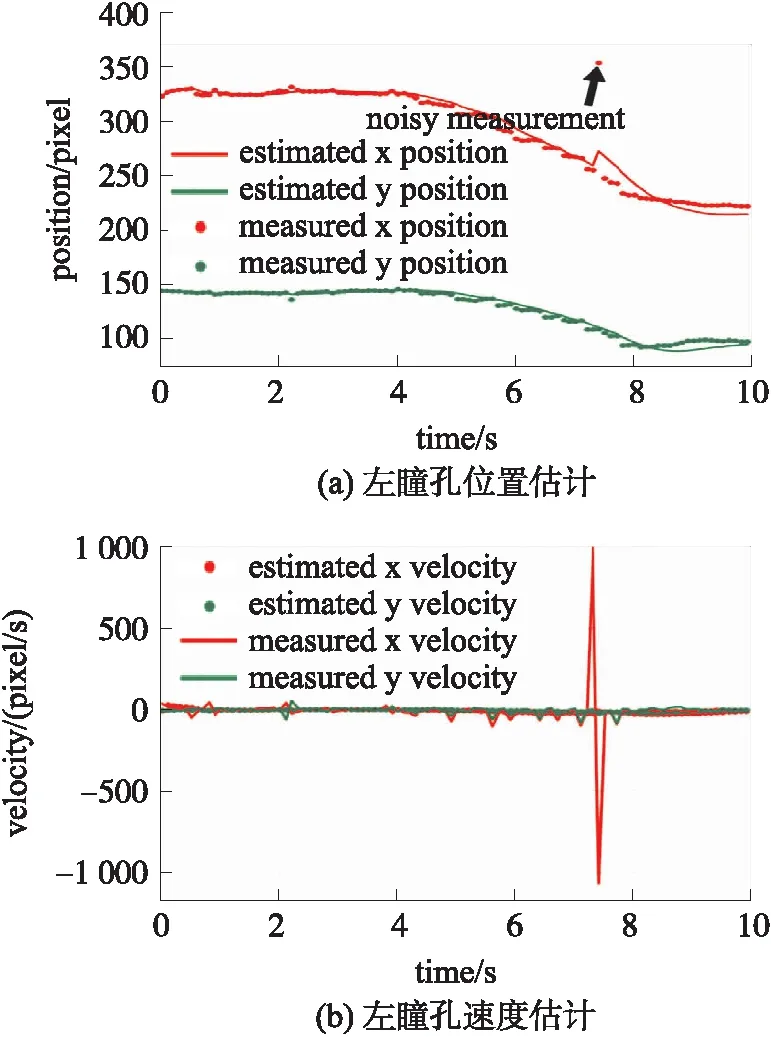
图4 常速度Kalman滤波器的左瞳孔位置与速度估计结果

3.4.2 常速度Kalman滤波器算法的实验结果及对比

图4是扫视屏幕对角线动作下常速度的Kalman滤波器的输出结果。图4(a)为常速度Kalman滤波器左瞳孔位置估计结果。实线为滤波器的x,y两个方向的位置估计结果,点线为测量结果。当在7.5 s左右时刻,位置测量存在噪声时,滤波器的输出存在着一个较大的抖动,抖动幅度约为15 pixel,为本文算法之下抖动幅度的300%。

图4(b)是常速度Kalman滤波器的左瞳孔速度估计结果,横坐标为时间,纵坐标为速度大小,其中离散点表示测量的速度结果(由相邻两个时刻的离散测量数据直接对时间求导所得),实线为速度估计结果。可见,常速度Kalman滤波器的输出速度估计上,存在一个1 000 pixel/s的抖动,而在本文算法之下无明显抖动。

另外,计算10维度的传统滤波器在执行单次Kalman模型计算时的乘法计算量,为5 686次。在MATLAB测试环境下,如表2所示,根据实验情况,数据量为100时(执行模型迭代计算100次),程序运行时间为0.060 13 s。如果将10维度传统滤波器拆分为3个滤波器,分别为为左右眼各4维的两个滤波器,以及两眼间距在xy轴上的分量2维滤波器进行叠加计算,所需时间为0.004 531 s。本文6维度的滤波器在执行单次Kalman模型计算时的乘法计算量为1 356次,程序运行时间为0.001 766 s,比10维度常速度Kalman滤波器加快了97%,比拆分后的常速度Kalman滤波器加快了61%。因此本文设计的滤波器简化了程序的运算量,在跟踪的快速性上具有一定优势。

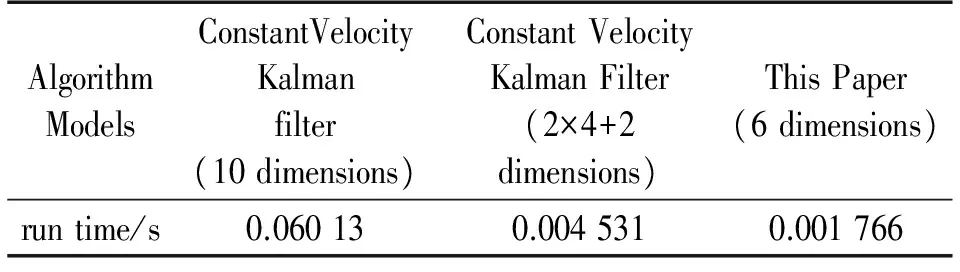
表2 3种算法模型运行时间对比

4 对预测注视点跟踪精度的影响

为探究本文算法对人机交互过程中预测注视点跟踪精度的影响,将未经过滤波算法计算得到的预测注视点、经过中心滑动平均的滤波方法(滑动窗口大小为7个数据点)得到的预测注视点、经过常速度Kalman滤波方法得到的预测注视点与经过本文算法得到的预测注视点位置进行比较。

实验过程中,首先令观察者注视屏幕中九宫格中心(白底图黑线相交处),再令观察者注视位于屏幕中央线上自左向右在10 s内匀速移动的动点,拍摄这两个动作下的眼部图像,获得瞳孔中心和角膜反射光斑中心坐标为实验数据。假定由注视屏幕九宫格中心获得瞳孔中心坐标(xp,yp)和角膜反射光斑中心坐标(xg,yg),则瞳孔—光斑相对偏移矢量可表示为:

xe=xp-xg,ye=yp-yg

(8)

假设(Xs,Ys)为屏幕上标记点的坐标,则用校准函数表示映射关系为[17]:

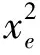
(9)

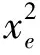
(10)

式(9)和(10)中共有12个待求解参数,将9组数据代入此二式获得共18个方程对参数进行求解,本文采用最小二乘法确定参数。将注视屏幕中央横线上动点获得的瞳孔—光斑相对偏移矢量数据代入上述模型得到注视点估计位置。根据实验过程,10s内屏幕中央线上匀速运动的点的实时坐标为注视点的准确位置。按照两种测试环境,即存在大扰动测量噪声和不存在大扰动测量噪声的情况,对以下4种滤波方法:未滤波、滑动平均滤波、常速度Kalman滤波、本文滤波算法4种方法分别预测注视点位置,并计算预测注视点坐标和注视点准确位置之间的距离误差。如表3所示,表中4行表示所使用的4种数据滤波处理方法,表中两列数据分别对应是否有大扰动测量噪声环境,可见本文算法模型下注视点估计结果误差最小,与常速度Kalman滤波算法相比,误差分别在无扰动与有扰动的情况下减小了21%与29%。

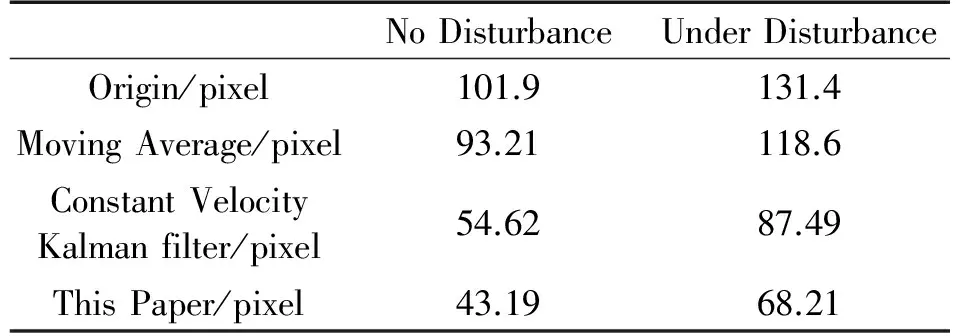
表3 4种算法模型下注视点估计结果误差对比

由注视点估计结果的误差对比可以看出,分别在存在大扰动测量噪声和不存在大扰动测量噪声的情况下,本文的滤波方法误差与常速度Kalman滤波方法以及滑动平均滤波方法相比,都具有最小的定位误差。综上所述,本文算法无论在计算量上,还是在人眼双目扫视下的注视点定位精度上,均具有一定的优势。

5 结语

本文将双眼扫视运动中拍摄的眼部图像作为研究对象,将瞳孔位置作为跟踪目标,构建了一种基于双眼同步运动特征约束的Kalman跟踪算法。仿真实验和实际注视点跟踪实验结果均验证了本文提出的算法在鲁棒性和快速性上均优于常速度Kalman滤波器以及滑动平均滤波器,对人机交互领域中的预测注视点位置定位跟踪的准确性的改善也大有帮助。注视点跟踪精度的提高,对进一步在心理学、医学、商业界面评估与设计等人机交互领域中开展相关研究都具有重要意义。

[1] 张琳琳,蒋敏,唐晓微. 基于眨眼修正卡尔曼滤波的人眼跟踪研究[J]. 计算机工程,2012,38(21):36-39.

[2] 李兵,戴尔晗. 基于人工神经网络的视线跟踪系统[J]. 计算机技术与发展,2015(4):98-101.

[3] Chang C J,Huang C W,Hu C W. Wearable Binocular Eye Tracking Targets in 3-D Environment Using 2-D Regression-Based Gaze Estimation[C]//IEEE International Conference on Consumer Electronics-Taiwan. Taiwan:IEEE,2016:1-2.

[4] 张琴. 基于瞳孔定位技术的视觉跟踪系统的研究[J]. 微型机与应用,2016,35(4):54-56.

[5] 杨庆华,张达磊,荀一,等. 面向人机交互的眼动跟踪方法研究[J]. 机电工程,2016,33(7):904-908.

[6] 邹云海,关蒲骏,杨波,等. 基于FPGA与投影算法的快速眼动跟踪系统实现[J]. 四川大学学报(工程科学版),2016,48(3):100-106.

[7] Zanetti M,Cecco M D,Fornaser A,et al. The Use of INTER-EYE for 3D Eye-Tracking Systematic Error Compensation[C]//International Symposium ELMAR-2016. Zadar:IEEE,2016:173-176.

[8] 朱小生,许烁. 基于卡尔曼滤波的运动目标速度测量[J]. 计量与测试技术,2016,4:9-12.

[9] 周承松,彭竞,刘文祥,等. 速度自适应约束卡尔曼滤波方法[J]. 传感技术学报,2016,29(8):1180-1185.

[10] 王江,付强,全权,等. 基于Kalman滤波和直方图匹配的双目视觉跟踪[J]. 新型工业化,2013,3(2):23-33.

[11] 王丽,郝晓丽. 基于kalman滤波器和改进camshift算法的双眼跟踪[J]. 微电子学与计算机,2016,33(6):109-112.

[12] Chi J,Xie L,ZhangP,et al. Hybrid Particle and Kalman Filtering for Pupil Tracking in Active IR Illumination Gaze Tracking System[J]. Mathematical Problems in Engineering,2014,2014(8):11-14.

[13] Li D,Winfield D. Starburst:A Hybrid Algorithm for Video-Based Eye Tracking Combining Feature-Based and Model-Based Approaches[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego:IEEE,2005:79-87.

[14] Grewal M,Andrews A. Kalman Filtering:Theory and Practice with MATLAB. New York:Wiley-Interscience,2015:195-214.

[15] 毛晓波. 仿生机器眼运动系统建模与控制研究[D]. 郑州大学,2011.

[16] Wang X,Ma X,QinB,et al. Control Strategy of Bionic Eyes Movement in Gaze Shifts[J]. Journal of System Simulation,2016,28(6):1380-1386.

[17] Jin Chun,Li Yaping. Estimation Method of the Fixation Point in Gaze Tracking System[J]. Science Technology and Engineering,2016,16(14):201-205.