驱动微梁形状对微陀螺仪耦合误差的影响分析*

郝淑英,张辰卿,齐成坤,李会杰,张昆鹏,陈 炜

(1.天津市先进机电系统设计与智能控制重点实验室,天津 300384;2. 机电工程国家级实验教学示范中心(天津理工大学),天津 300384)

微机械陀螺仪是一种利用哥氏效应来测量物体转动角速率的惯性传感器,与传统的陀螺仪相比,具有性价比高、尺寸小、重量轻以及动态性能好等特点,广泛应用于航空航天、军事、汽车工业和消费电子等领域[1]。由于微陀螺仪是基于微机械加工技术而研制成的新型陀螺仪,加工的相对精度较低,且一次成型,尺寸无法修正,易产生加工误差[2]。所以微陀螺仪会经常存在支撑梁刚度不对称的现象,导致驱动运动耦合到检测方向从而导致陀螺仪的输出产生偏差,严重影响了微机械陀螺仪的性能[3],因此分析由支撑梁加工误差引起的正交耦合以及模态耦合现象十分必要。

侯占强[4]研究了弹性梁制造误差对微陀螺零偏稳定性的影响机理,以及抑制方法。刘学[5]等提出了一种正交误差闭环控制自补偿方法,降低了正交误差,使微陀螺零偏输出均值从778 mV减小到了2 mV。施芹[6]等人对不等弹性、阻尼不对称、质量不对称这3种加工误差引起的机械耦合误差进行了理论分析,指出正交耦合误差是机械耦合误差中主要的误差信号,且主要误差源是支撑梁不对称。裘安萍[7]以一种SZG1微陀螺为研究对象,通过对内、外支撑梁的结构改进,有效地减小了微陀螺的正交误差。郑怡文[8]等全面分析了正交误差产生的主要因素,并论述了如何减小加工误差带来的正交误差。姜劭栋[9]等人建立了正交耦合系数的理论分析模型,提出了加工误差和正交耦合系数的关系,指出加工误差影响最大的情况是同一对角线上微梁的尺寸同时增大或减小。贺琨[10]等人提出了振动结构支撑梁的加工误差会引起结构刚度不对称并产生模态耦合误差,并采用紫外激光微细加工技术进行修正,使微陀螺样机模态耦合误差信号的峰值从2.88 V降低到0.24 V。

考虑同一对角线两驱动微梁的梁宽同时减小或增大的加工误差情况对检测质量块在驱动模态时的耦合程度影响最大[11],本文以同一对角线上微梁的尺寸同时增大或减小这一影响最大的加工误差的梳状微陀螺为研究对象,研究U形微梁一端梁长变化对微陀螺正交耦合、模态耦合以及对输出信号的影响,为微陀螺微梁设计、误差修正及补偿提供指导。

1 梳状微陀螺的有限元模型的验证

直弹性梁在加工时,经过高温氧化、键合和掺杂等许多工艺,都会使其结构产生加大的残余应力,对微陀螺的灵敏度、带宽等性能产生影响。为降低直弹性梁对微陀螺带来的不利影响,本文在保持微梁刚度不变的条件下,设计了驱动微梁为U型梁和检测微梁为蟹脚型梁的微陀螺模型,将文献[12]中的直梁微陀螺改进成蟹脚型和U型梁,改进后的模型如图1所示。本文选择solid195单元,采用多晶硅材料参数,其密度ρ=2.33×103kg/m3,泊松比μ=2.78,弹性模量E=169 GPa,采用自动划分网格方式,为保证计算精度选用自动网格化分中精度最高的等级,共划分了38 478个单元,微陀螺的有限元模型如图2所示,微陀螺驱动模态的等效质量为mx=2.007×10-9kg,检测模态的等效质量为my=0.907×10-9kg。有限元分析得出驱动模态的固有频率ωd=29.64 kHz,检测模态固有频率ωs=29.90 kHz。

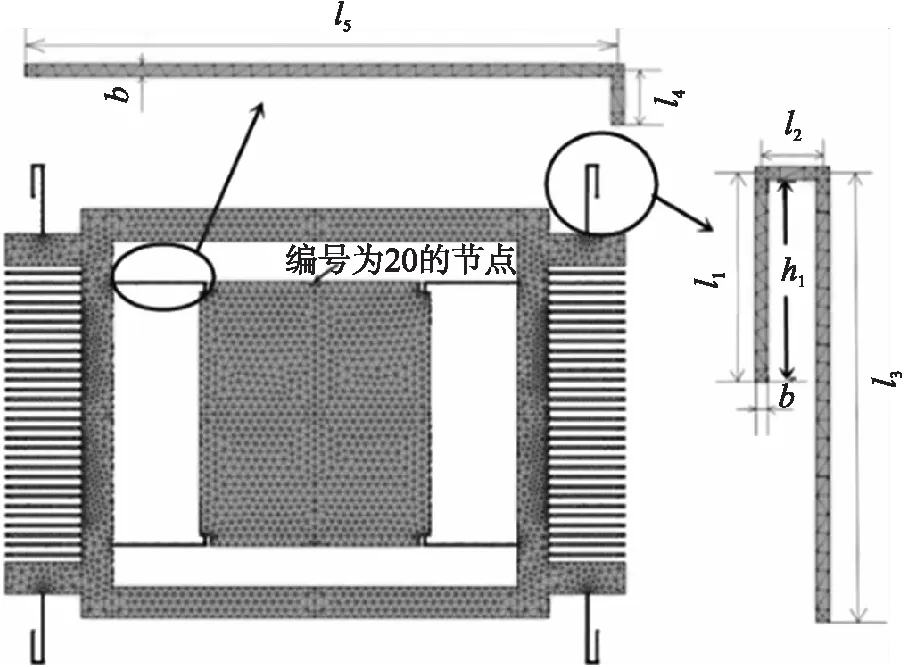
图2 微陀螺有限元分析模型

采用能量法求出U形梁驱动方向和蟹脚梁检测方向的刚度表达式[5]为:

驱动模态和检测模态的固有频率为:

(1)

由式(1)计算得驱动模态和检测模态对应的固有频率值为30.30 kHz、30.49 kHz;与有限元结果比较可知驱动模态固有频率误差为2.18%,检测模态固有频率误差为1.94%,由此验证了有限元分析模型及分析方法的可靠性。

2 驱动微梁形状对正交耦合误差的影响

加工误差导致各微梁的刚度产生差异导致结构的弹性不对中即刚度矩阵为非对角阵,使得检测质量块的运动轨迹不再是与驱动轴线重合,驱动方向和检测方向不能完全垂直,即使没有输入角速度,驱动振动也会在检测方向产生一个误差分量,因此在加工误差不可避免的情况下,有必要对支撑梁形状对正交误差的影响规律进行分析。微陀螺仪驱动支撑梁的总刚度矩阵为:

同一对角线两驱动微梁的梁宽同时减小(或增大)的加工误差情况下微陀螺的梁宽不等结构如图1所示。鉴于其他两种情况下的梁宽误差对系统的影响比较小,选择在模态耦合最严重的微梁梁宽误差下研究不同微梁形状对梳状微陀螺驱动模态耦合的影响规律,图中的Δi(i=1,2,3,4)是驱动微梁梁宽的相对误差。驱动微梁的弹性刚度与惯性矩成正比,是梁宽b的三次方,当Δ很小时,可忽略Δ的高阶项,得到微陀螺驱动方向的刚度矩阵[7]为:

(2)

kxx为x轴方向的刚度,kyy为y方向的刚度,kφzφz为绕z转动的刚度,kxy为x轴和y轴之间的耦合刚度,kxφz为x轴和绕z轴之间的耦合刚度,kyφz为y轴和绕z轴之间的耦合刚度。本文取梁宽误差为:Δ1=Δ4=5%,Δ2=Δ3=-5%,将Δi(i=1,2,3,4)值分别代入式(2)得:

(3)

U型梁在检测方向以及耦合方向的刚度系数为:

(4)

(5)

当弹性系统的总刚度矩阵的非对角线上的元素不为零,在没有角速度输入时,驱动方向x的运动会传导至检测方,沿检测方向y产生位移,此时驱动模态下检测方向和驱动方向的位移比值为:

(6)

考虑式(3)由式(6)得:

(7)

根据式(7)得出同一对角线两驱动微梁的梁宽同时减小(或增大)的加工误差情况下微陀螺正交耦合误差随梁长h1的变化规律如图3所示。

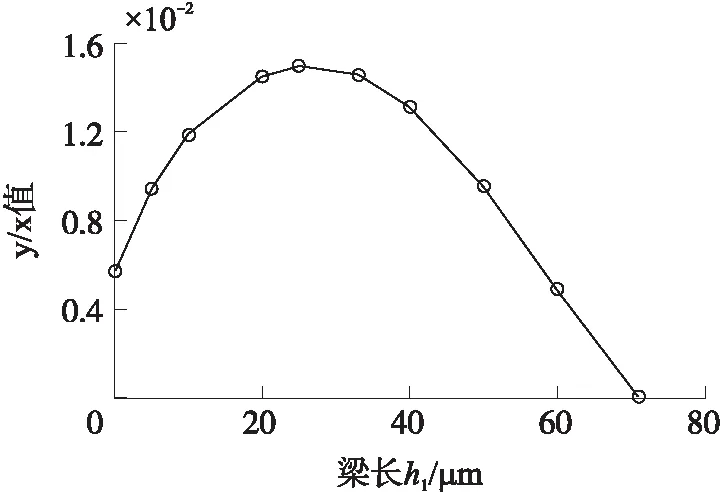
图3 正交耦合误差随梁长h1的变化规律

微梁加工误差导致的正交耦合误差随着梁长h1长度的增加呈现先增后减的变化规律,当h1=30 μm～32 μm时微陀螺驱动与检测方向正交耦合程度达到峰值;此后,正交耦合程度随h1不断增大而逐渐减小,当h1=70 μm即微梁变成等长U型梁时,正交耦合误差为零。所以在设计微梁形状的时候要尽量选择等长U型梁或者直弹性梁。这样才能最大化降低因正交耦合误差带来的影响,同时在加工中应从工艺上改进,尽量减少两对角线微梁尺寸相同的加工误差。

3 驱动微梁形状对模态耦合的影响

由加工误差导致的弹性不对称会引起模态耦合即在驱动模态时检测质量块会沿检测方向发生移动,反之亦然,由此造成微陀螺在检测方向出现较大的干扰信号。图4～图6分别表示当h1为0 μm、32 μm、70 μm时微陀螺的驱动模态和检测模态。

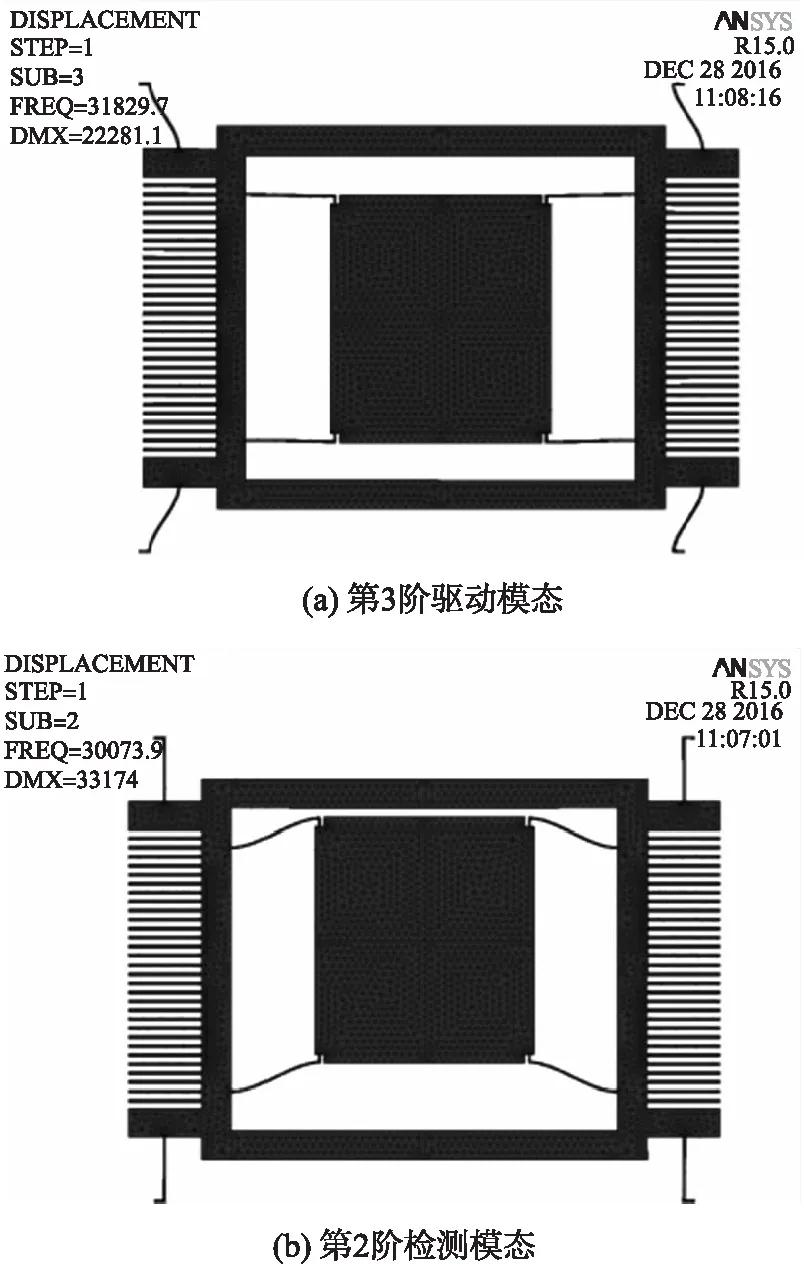
图4 h1为0 μm时微陀螺工作模态图

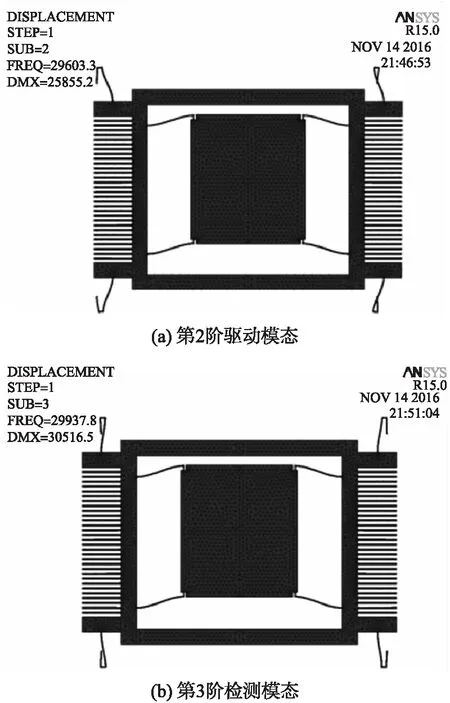
图5 h1为32 μm时微陀螺工作模态图

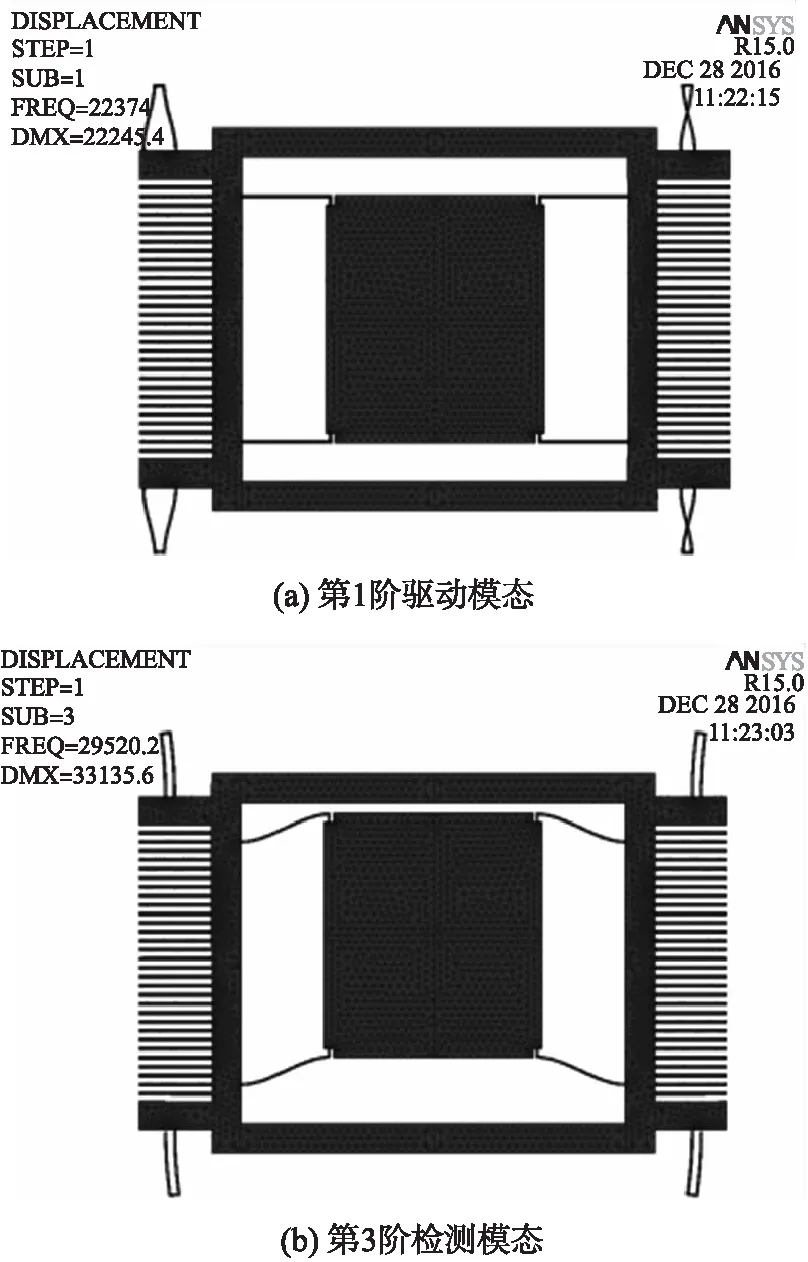
图6 h1为70 μm时微陀螺工作模态图

由图4可知当h1为零时相当于U型梁退化为直梁时驱动模态下检测质量块在检测方向仅有微小的位移。当h1=32 mm时驱动模态下检测质量块在沿检测方向以及检测模态下驱动质量沿驱动方向都产生了相当大的位移,如图5所示;由图6可知当U形梁两端梁长相等时驱动模态下检测质量块沿检测方向没有位移,检测模态下驱动方向仅有微小位移。

分别取h1的长度为0 μm、5 μm、10 μm、15 μm、20 μm、25 μm、30 μm、32 μm、35 μm、40 μm、50 μm、60 μm、70 μm,其他尺寸不变,分别建立这13种微陀螺的有限元模型,进行模态分析,分析同一对角线微梁尺寸相同的加工误差下梁长h1对微陀螺模态耦合的影响规律。在检测质量块上选取编号为20的节点,分别量取该节点在驱动模态时检测方向的位移y与驱动方向的位移x,得到y/x的比值,比值越大模态耦合越强。驱动模态下y/x的比值随梁长h1的变化关系如7图所示。

图7 模态耦合随梁长h1的变化规律

当h1从0 μm到32 μm变化时微陀螺驱动模态与检测模态耦合程度逐渐增大;当h1从32 μm到70 μm变化时,微陀螺驱动模态、检测模态耦合程度逐渐降低。梁长h1=0 μm或h1=70 μm时,微陀螺驱动模态耦合程度非常微小;当梁长h1=32 μm时,微陀螺驱动模态耦合程度达到最大。对比图3与图7可知驱动模态耦合随梁长h1的变化规律与正交耦合误差随梁长h1的变化规律基本相同,两者呈现正相关。根据式(4)、式(5)和式(7)可知,影响正交耦合误差的主要是驱动微梁的尺寸,但模态却取决于微陀螺的特征矩阵即不仅包含驱动微梁还包含了检测微梁尺寸及其两者质量的影响,因此图3中的曲线比值与图7中的比值会有差别。

4 驱动微梁形状对检测信号的影响

由于微陀螺试件为微米级,其加工成本过高,同时实验装置也比较复杂,实验验证存在一定的困难。微陀螺工作时,在两端的驱动电极施加带有直流偏置的交流电压,梳齿间产生交变的静电力,本质上为简谐激振力,因此本文采用有限元仿真实验对微陀螺沿驱动方向施加简谐激励模拟交流电压作用下微陀螺的响应,研究驱动微梁存在加工误差条件下U形梁h1的长度对微陀螺输出结果的影响。

根据前面分析所得的驱动模态的固有频率选定谐响应分析的频率范围,使驱动方向的固有频率在该激励频率范围的中间位置,给定20个步数,在动梳齿左端面施加简谐激振力,直流偏置电压Vdc=10 V,交流电压Vac=4 V时静电力的幅值为F=6.372×10-8N,微陀螺整体的空气阻尼系数为C=1.362×10-6kg/s。图8为h1为0 μm、32 μm、70 μm时节点20在驱动、检测方向的幅频响应曲线。

当h1=0和70 μm时驱动方向施加激励时对检测信号的干扰很小,当h1=32 μm时驱动方向施加激励时在无外界角速度输入的情况下对应于激励频率等于驱动频率时检测方向产生了很大的位移,此时正交耦合误差的影响最大,其原因为驱动方向的运动由于耦合作用在检测方向生成一个简谐变化的运动分量,相当于给检测模块施加了一简谐激励,当驱动模态与检测模态频率相近时意味着检测的激励频率与检测的固有频率相近,检测发生共振,所以此时的耦合作用最强。因此对于单自由度微陀螺应适当加大驱动和检测的模态频率差,即可起到适当增加带宽的目的又能降低耦合的影响。

图8 梁长h1对检测信号的影响

图8给出了交流电压的频率等于驱动频率时节点20驱动方向的位移与检测方向的位移比随h1的变化关系。当微梁梁长h1由0 μm到70 μm变化时,检测方向的位移首先是逐渐增加并接近驱动方向的位移,在32 μm达到峰值,随后又逐渐降低。

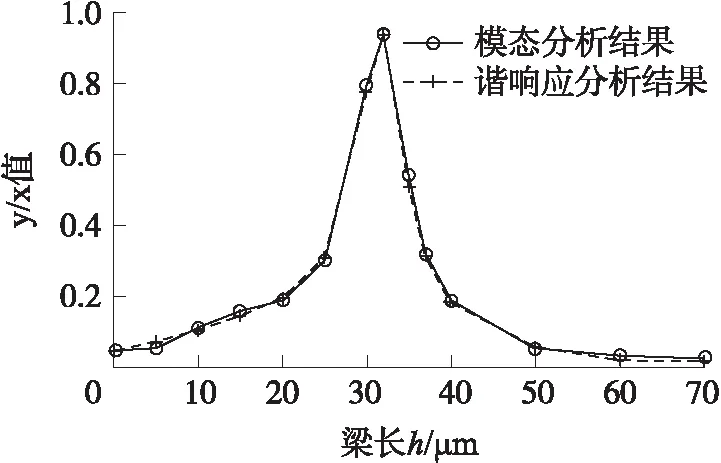
图9 y/x值随不同梁长h1的变化规律

由图9可知,模态分析结果和谐响应分析结果相互验证,表明了随着梁长h1的增大,节点20的检测方向位移y与驱动方向位移x的比值先增大后减小,且两者变化趋势基本吻合。即当梁长h1=0 μm或h1=70 μm时,微陀螺驱动模态耦合程度非常微小;当梁长h1=32 μm时,微陀螺驱动模态耦合程度达到最大。为了避免在设计过程中发生更加严重的模态耦合,微梁应该设计成等长的U型梁或者直梁,这与避免正交耦合误差中得到的设计原则也是吻合的。

5 结论

在同一对角线两驱动微梁的梁宽同时减小或增大的加工误差情况下,U形梁一端梁长的变化对正交耦合误差、模态耦合及检测信号产生极大影响,在加工中应尽量避免或减小这类误差的发生;U型梁退化为直梁或为完全对称的形状时,同一对角线两驱动微梁的梁宽同时减小(或增大)的加工误差所引起的的正交耦合误差、模态耦合及对检测信号的影响可略去不计;当U型梁一端的梁长为另一端长度的二分之一左右时该类加工误差会引发非常严重的模态耦合现象并对检测信号产生极大影响,在设计与加工中要尽量避免此类情况的发生;对于单自由度微陀螺应适当加大驱动和检测的模态频率差,既可起到适当增加带宽的目的又能降低耦合的影响。

[1] 陈尚,张世军,穆星科. MEMS 陀螺技术国内外发展现状简述[J]. 技术与应用,2016,22(4):19-23.

[2] Han J S,Kwak B M. Robust Optimal Design of a Vibratory Microgyroscope Considering Fabrication Errors[J]. Micromechanics and Microengineering,2001,66(11):662-671.

[3] Yang Bo,Zhou Bailing,Wang Shourong. Quadrature Error and Offset Error Suppression Circuitry for Silicon Microgyroscope[J]. Journal of Southeast University:English Edition,2008,24(4):487-491.

[4] 侯占强. 蝶翼式微陀螺零偏稳定性提升关键技术研究[D]. 国防科学技术大学,2012.

[5] 刘学,陈志华,肖定邦. 动式微陀螺正交误差自补偿方法[J]. 传感技术学报,2012,25(9):1221-1225.

[6] 裘安萍,施芹,苏岩,等. 微陀螺仪的机械耦合误差分析[J]. 精密工程,2008,16(5):894-898.

[7] 施芹. 提高硅微陀螺仪性能若干关键技术研究[D]. 南京:东南大学,2006.

[8] 郑怡文,白云辉,彭超. 微陀螺仪的正交误差控制分析[J]. 电子技术与软件工程,2015,4(5):143-144.

[9] 姜劭栋,裘安萍,施芹,等. 硅微陀螺仪正交耦合系数的计算及验证[J]. 光学精密工程,2013.

[10] 贺琨,崔红娟,侯占强,等. 微机械振动陀螺模态耦合误差分析与激光修形方法研究[J]. 传感器与微系统,2013,32(3):21-24.

[11] Iyer S V. Modeling and Simulation of Non-Idealities in az-Axis CMOS-MEMS Gyroscope[D]. Pittsburgh:Carnegie Mellon University,2003.

[12] Phani A S,Seshia A A,Palaniapan M,et al. Coupling of Resonant Modes in Micromechanical Vibratory Rate Gyroscopes[C]//Boston,Massachusetts,USA,2004 NSTI Nanotechnology Conference & Trade,2004:335-338.

[13] Gary K. Simulation of Microelectromechanical Systems[D]. American:Engineering-Electrical Engineering and Computer Science,University of California,Berkeley,USA,1994.