链条桌边下落问题的探究
2018-02-05李岩松
陈 思 李岩松
(1清华大学机械学院汽车工程系,北京 100084; 2清华大学物理系,北京 100084)
“链条(软绳)下落”的习题经常出现在一些高中和大学的物理题目中,用来考察学生对于动量守恒和功能原理的理解和应用。有很多专家和学生对这类习题进行了深入的讨论和分析[1-4]。文献[5]就链条中科学问题介绍了国内外进展,而文献[6]则从教学角度对这一话题进行了梳理。为了能够在有限的时间之内,得到这类问题的答案(这样教师“教”和学生“学”都显得有“信心”),自然要对问题进行简化和理想化。链条被简化成“细”“软绳”和“质量均匀分布”,对限制绳的接触面简化成“光滑”。这些简化在解题中是被默认了。另外一个非常关键的默认简化是绳子始终与光滑接触面接触。这个简化则有待深入分析。
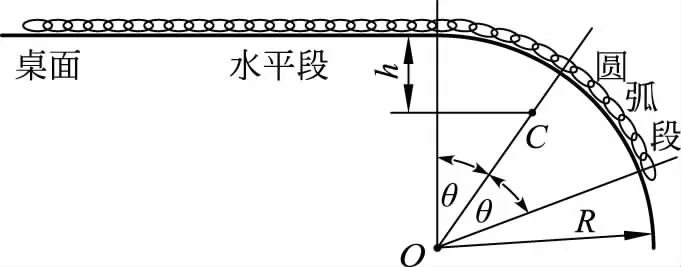
图1 链条下滑示意图
本文以图1所示的链条沿圆弧形桌边下落模型论证了链条会飞离桌边的依据,确定了飞离点位置,最后对相关文献中的有关飞离问题进行了讨论。
1 飞离分析
1.1 速度
图1中,柔软细链条的质量均匀分布;长度为l;线密度为λ;桌边的圆弧半径为R。接触面光滑。假设链条一端从桌边圆弧的起始位置被触发下滑,初始速度为零。
不失一般性,先假定初始阶段链条与圆弧段贴合,一直运动到图1所示的2θ角位置。整个链条沿桌面绷紧运动,故各点速率v相同,因此链条动能Ek为
图1中的链条圆弧段的重心位于C处,由理论力学得知
因此,圆弧段质心下降高度为
根据机械能守恒,有
即
(1)
1.2 支持力
链条内部有张力T,此张力沿链条的切线方向,但是会随链条内断面位置的变化而变化。用s表示链条断面的位置,则链条内部张力的矢量形式为T=T(s)τ,其中τ为切向单位矢量。在数学上T=T(s)τ就如同弧坐标中的速度=v(s)τ。类似于从弧坐标的速度到加速度,我们分析dT/ds,有
即
(2)
其中,n为链条的法向单位矢量;ρ为链条的曲率半径。
显然柔软链条与柔弱细绳没有本质差异。为了便于画图显示,把链条画成横断面沿链条完全不变的柔软细绳。考察细绳在桌角圆弧段上的一个微元段ds,见图2。由式(2)有
(3)

图2 柔软细绳下滑示意
沿法向对微元运用牛顿第二定律,有
(4)
即
(5)
式(4)对桌子水平面也是成立的,只不过ρ=∞。此时还有β=0,因此dN=λgds,它不会小于零。这表明链条始终与桌子水平面有压力,因而水平段不可能跳起来。
链条不能抗压,所以张力T总是大于零的;它在链条两端等于零,因为是自由的边界。如果链条足够长,在水平段有足够的长度,那么从β=0到β=θ,圆弧段的张力必然单调减小,即式(5)第二项是单调减,第一项对β也是单调减的,而第三项不随β变化。综上,dN最小应发生于β=2θ,此处又有T=0,故在链条的下落末端有
1.3 飞离
末端飞离的临界条件为dN=0
即
(6)
引入γ=π/4-θ,式(6)可写为
(7)
对R/l很小的情形,γ必然很小,此时就有sinγ≈γ;cos2γ≈1,从式(7)可近似解得γ≈πR/l,即下落端到:
2θ=2(π/4-γ)≈π/2-2πR/l
(8)
链条末端就会飞离。
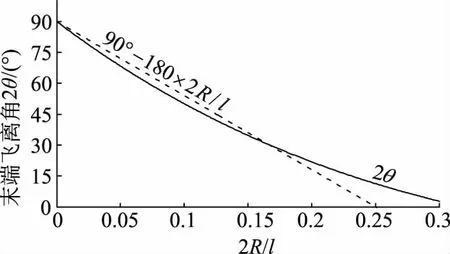
图 3
对R/l不是很小的情形,式(5)要用数值法求解。利用Matlab的fminsearch求出的结果如图3所示。
图3和式(8)表明,只有当R/l→0时,才可能2θ=π/2(=90°),即链条末端在脱离桌面时垂直下落。只要R/l非零,则链条末端并不会一直沿圆弧段滑动到垂直才下落,而是在未到垂直之前就会飞离。
R/l=0的情形物理上不可实现,在数学考察R/l→0,那么式(5)中第三项将趋近于负无穷(ρ=R),更无法保证dN≥0,也就是更不可能保证绳与桌角贴合。
综上所述,图1所示的问题中:链条脱离桌面后不可能保持垂直;下落的端点在达到垂直之前就应该飞离。
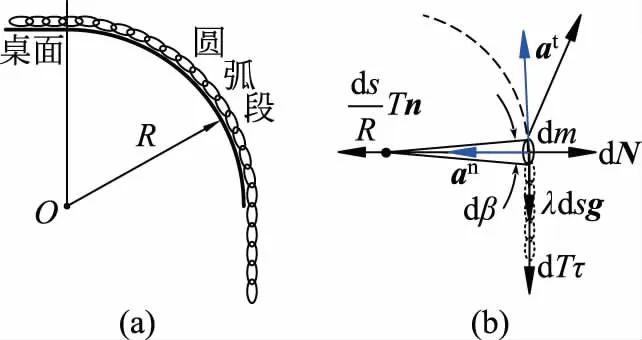
图 4(a) 模型; (b) 最后一环分析
2 讨论
(1) 文献[1]中例2的链条已经悬垂于桌面下,从静止再释放。这也不能保证链条与桌角的贴合。论证如下。
式(5)也适用于链条末端已垂于桌面之下。对桌角半径R/l→0的情形,第三项必然是趋于负无穷,无法保证贴合条件dN≥0。
对R/l有限的情形,采用反证法,即先假定链条与桌角一直贴合。我们来分析链条最后一环,它在离开桌面之前的受力分析如图4(b)所示,其中链条张力按照式(3)分解了。由于处于链条末端,所以进一步有T=0,这样沿水平方向就有
-dN=λdsg×an=λdsg×v2/R>0
即dN<0。这表明假设错误。真实情形应该是在脱离之前,某段链条会飞离桌面。
(2)文献[2]分析了图5所示的软绳沿桌面小孔下落的问题。该文作者分别采用了动量定理和动能定理两种方法,发现二者结果不一致。实际上软绳自小孔边缘下落,与图1的模型类似,软绳会飞离小孔的倒角圆弧。如果小孔很小,那么飞离的软绳必然与小孔的内壁碰撞,因而落下段不能保持直线。如果小孔小到在孔内段,绳子近似保持直线,那么绳子到小孔的下方也不能保持直线。因此,文献[2]计算落下段的动能和动量的方式值得深入分析。

图5
(3) 文[6]讨论了链条在滑轮上下落的问题,研究了链条从滑轮上飞离的条件,但是由于微元段没有考虑重力,所以飞离条件应按式(5)重新分析。
如果张力在图1弧形段的大小可以近似相等(在1.2节的分析中没有承认它近似相等),那么随弧上位置变化的是β。当β=90°时,式(5)右边最小,它对应最容易飞离的位置(而不是文献[6]中的β=0)。在此位置,飞离条件为
T=λv2/R
如果T沿弧形段的大小变化很明显,则确定飞离位置和飞离条件还是很麻烦的。
3 结语
从上文分析我们可以看出,对于“链条桌边下落模型”的分析是较为复杂的,很难在没有计算机辅助的情况下进行求解、分析。为了出题方便而简化的条件不仅不会帮助学生掌握知识,还会错误地引导学生。因此高中和大学的考试中,应当
避免利用该模型对“动量守恒”“功能原理”知识点进行考察。本文对于“飞离”这一过程的讨论还不全面,应当继续求解飞离的水平方向速度,可以尝试通过对“链条受力”的积分计算,求链条水平方向受到桌子的作用力,进而利用“水平方向动量定理”求出飞离的速度。
[1] 杨元平,高翔. 对机械能守恒定律“五性”的理解[J]. 物理教师,2003(10): 4-6. YANG Yuanping, GAO Xiang. Understanding conservation law of mechanical energy from 5 aspects[J]. Physics Teachers, 2003(10): 4-6. (in Chinese)
[2] 吴海娜, 刘顺, 公卫江,等. 用微元法巧解软绳下落过程的能量损失[J].物理与工程,2016,26(1):72-75. WU Haina, SHUN Liu, GONG Weijiang, et al. The energy loss of the falling process of soft rope using microelement method[J]. Physics and Engineering. 2016, 26(1): 72-75.
(in Chinese)
[3] 刘斌. 充分发挥习题的作用培养学生独立解决问题的能力[J]. 物理与工程, 2014, 24(4): 11-19. LIU Bin. To give full play to the role of exercises to cultivate students’ ability to solve problems independently[J]. Physics and Engineering, 2014, 24(4): 11-19. (in Chinese)
[4] 郑国安.下降链条的能量损失[J].物理教师,2005,26(5):41-42. ZHENG Guoan. The energy loss of the descending chain[J]. Physics Teachers, 2005, 26(5): 41-42. (in Chinese)
[5] 于同旭,张文彬,许腾,等. 链条下落运动问题浅析[J].自然杂志,2015,37(1):53-60. YU Tongxu, ZHANG Wenbin, XU Teng et al. Discussion of the chain falling movement[J]. Chinese Journal of Nature, 2015, 37(1): 53-60. (in Chinese)
[6] 路峻岭,秦联华,任乃敬. 关于柔软细绳运动问题中加速度奇点的讨论[J].大学物理,2016,35(12):7-12. LU Junling, QIN Lianhua, REN Naijing. Discussion on the speed singularity of soft string movement[J]. College Physics, 2016, 35(12): 7-12. (in Chinese)
