带电粒子在磁场中运动规律的可视化研究
2018-02-05姚琴芬束正煌
姚琴芬 束正煌
(江苏开放大学通识教育学院,江苏 南京 210036)
研究带电粒子在磁场中运动的规律时,可以利用Matlab强大的模拟仿真功能[1,2],把复杂、抽象的物理规律,通过直观、生动的物理图像展现出来。同时,我们可以随意更改仿真参数,输出不同条件下的仿真图像。对于有些解析法无法求解的复杂问题,只要给定初始条件,我们也可以通过Matlab软件的强大计算功能进行数值求解,这一点,在实际工作中有着重要的意义。
1 几个应用实例[3]
(1) 磁聚焦[4,5]
如图1所示,一束质量为m、带电量为e的电子,先经过较大的轴向电压加速,获得相同的水平速度vz;再经过径向交变电压发散,获得不同的但很小的径向速度vr;然后进入轴向匀强磁场B中做螺旋运动。下面分析这束带电粒子的运动轨迹:

图1 磁聚焦原理图
螺旋运动的半径由径向速度vr决定,其值为
(1)
根据公式(1),各粒子将作半径不同的螺旋运动。
螺旋运动的螺距由水平速度vz决定,其值为
(2)
根据公式(2),由于各粒子具有相同的水平速度vz,所以,它们的螺距相同。下面,根据粒子的运动方程,用Matlab描绘其运动轨迹。
由于电子带负电荷,其运动方程可表示为
(3)
其中,Cx,Cy和Cz是常数,如果t=0时,x=y=z=0,则Cx=-R,Cy=Cz=0。
设发散角的正切tanθ=vr/vz,则半径可表示为
(4)
以管长L为坐标单位,取周期T为时间单位,运动方程可化为约化形式,即
(5)
其中,t′=t/T。取发散角θ为参数向量,取时间t为自变量向量,形成矩阵,计算三维坐标,用三维矩阵画线法画出轨迹曲线族如图2所示:
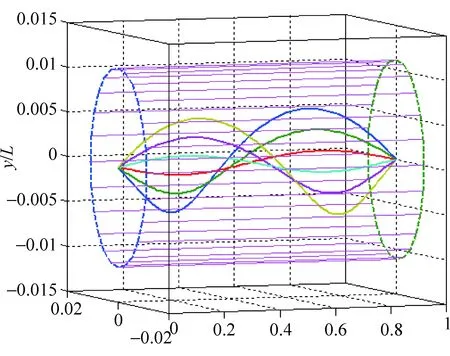
图2 电子束磁聚焦轨迹图
从图2可以看到,由于各个电子的径向速度不同,因此,每个电子各自以不同的半径做螺旋运动,但由于各电子具有相同的螺距,因此,经过一个周期后,它们又重新会聚到同一点,这种现象叫做磁聚焦。改变观察角度,从右向左看,可以看到,所有电子的运动轨迹都是圆,如图3所示。且电子束的发散角越大,它做螺旋运动的半径就越大,每经过一个周期,电子束就会聚一次。
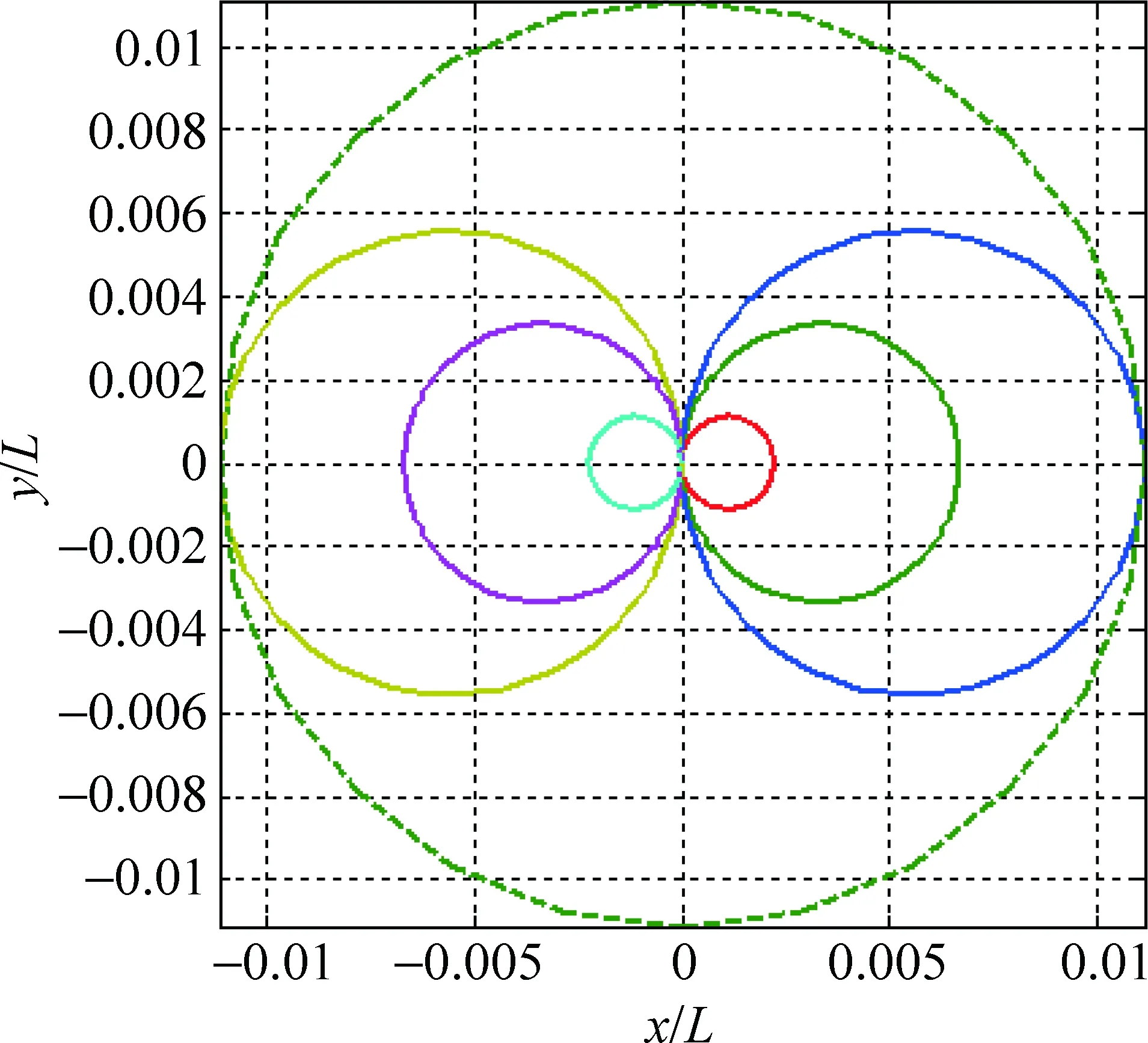
图3 磁聚焦侧面示图
程序如下:
clear %清除变量
theta=-2:0.8:2; %发散角向量的度数
th=theta*pi/180; %化为弧度
n=1; %整数(焦点或周期个数)
t=linspace(0,n); %时间向量
[TH,T]=meshgrid(th,t); %矩阵
X=tan(TH)/2/pi/n.*(cos(2*pi*T)-1);
%x坐标
Y=tan(TH)/2/pi/n.*sin(2*pi*T);
%y坐标
Z=T/n; %z坐标
figure %创建图形窗口
box on %加方框
grid on %加网格
view(-20,5) %设置视角
fs=16; %字体大小
r=max(abs(X(:))); %圆的半径
x=r*cos(th); %圆的横坐标
y=r*sin(th); %圆的纵坐标
hold on %保持图像
%画磁感应线
pause %暂停
view(90,0) %设置左视角
axis equal tight %使间隔相等
《庄子》有篇《不龟手之药》(龟通皲,皮肤皲裂之意),讲了一个故事:宋国有一个善于制造防治皮肤冻裂的药(类似于现在的防冻护手霜)的人,世世代代以在水中漂洗棉絮为业。有一个客人听说了,请求用百金购买这个药方。宋国人把族人召集在一起商量说:“咱家世世代代以在水中漂洗棉絮为业,不过赚几个小钱儿罢了。现在一下子卖掉技术就能得到百金,那就卖给他吧。”客人得到秘方以后,用它来游说吴王。正赶上越国向吴国发难,吴王派客人作大将,冬天与越国人在水中作战,因为客人有制作护手霜的秘方,将士们免受冻伤,吴军大获全胜。论功行赏,吴王赏给这个客人一块封地。
(2) 带电粒子在非匀强磁场中的运动规律[6,7]
如图4所示: 一质量为m、电荷量为q的粒子,以初速度v0,从坐标原点出发,在xy平面内,沿与x轴夹θ角的方向进入非均匀磁场中,磁感应强度B的大小与x成正比,B=B0x,方向沿x正方向。试写出该带电粒子的运动方程,并描绘它在这一非均匀磁场中运动的轨迹[8](忽略重力作用)。
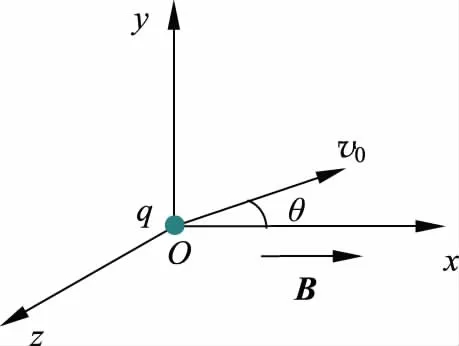
图4 带电粒子进入非均匀磁场
分析求解: 该带电粒子在非均匀磁场中仅受洛伦兹力的作用,因此运动方程为
(6)
(7)
根据速度与位置的关系方程有
(8)
在初始条件t=0时,x=y=z=0,vx=v0cosθ,vy=v0sinθ,vz=0。联立求解(7)、(8)两式组成的6个一阶微分方程组,可以得到3个位置(x,y,z)以及3个分速度(vx,vy,vz),但求解过程比较复杂。我们利用Matlab强大的数学工具,编制下列程序,可很方便地解出方程组,并描绘出带电粒子在这一非均匀磁场中运动的轨迹。假设v0=1000m/s,θ=30°,qB0/m=100。
程序如下:
%电荷在非均匀磁场中的运动
clear
global A; %定义全局变量
A=100;v=1000;sita=pi/6; %设定qBo/m,初速度,入射角
vx=v*cos(sita);vy=v*sin(sita);
%计算x,y方向的初速度
tspan=[0 0.1]; %设定积分时间
subplot(2,2,1) %以下为描绘各方向的运 动轨道
plot(t,y(:,1)); %绘制一般二维曲线
%comet(t,y(:,1)); %绘制动态二维轨迹
subplot(2,2,2)
plot(t,y(:,3));
%comet(t,y(:,3));
subplot(2,2,3)
plot(t,y(:,5));
%comet(t,y(:,5));
subplot(2,2,4)
plot(y(:,3),y(:,5));
%comet(y(:,3),y(:,5));
figure %新开图像窗口plot3(y(:,1),y(:,3),y(:,5)); %绘制一般三维曲线
%comet3(y(:,1),y(:,3),y(:,5));
%绘制动态三维轨迹
函数文件是一个独立文件,文件名为dzc.m
%电荷在非均匀磁场中运动的微分方程
function yp=dzc(t,y)
global A; %定义全局变量yp=[y(2) 0 y(4) A*y(6)*y(1) y(6)-A*y(4)*y(1)]; %写入微分方程
程序通过求解方程组,得到了全部位置和速度分量与时间点的数值关系,因此,运行程序后,可一一画出带电粒子在非均匀磁场中的运动轨迹图如图5所示。
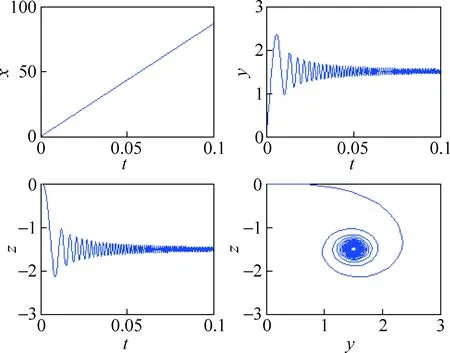
图5 带电粒子在非均匀磁场中各个方向的运动图像
从图5可以清楚地看到:在x方向,带电粒子因没有受到任何力的作用而作匀速直线运动;在y和z方向,带电粒子在磁场与x成正比增强的洛伦兹力的作用下,运动轨迹呈半径逐步变小的螺旋形[9]。图6是带电粒子在三维空间中的螺旋形运动轨迹。

图6 带电粒子在非均匀磁场中的运动轨迹
2 结语
通过Matlab模拟仿真技术,不仅可以算出解析法无法计算出来的结果,而且能把带电粒子在磁场中的运动轨迹直观、准确地描绘出来,通过动画观察物理过程的细节[10],不同参数的自由选取,使学生能更透彻地理解物理现象及规律背后的奥秘,同时,还能培养学生利用数值计算和模拟[11]解决物理问题和其他工程问题的兴趣与能力。
[1] 华玲铃,杨阳.大学物理教学中培养科学计算能力的研究
[J]. 物理与工程,2013,23(3):37-41. HUA Linlin, YANG Yang. Research on the cultivation of scientific computing ability in college physics teaching[J]. Physics and Engineering, 2013, 23(3): 37-41. (in Chinese)
[2] 吕波,饶黄云.大学物理教学中融入数值计算与模拟技术的研究[J].东华理工大学学报,2013,32(1):74-77. LV Bo, RAO Huangyun. The research on the application of numerical calculation and simulation technology in the teaching of college physics[J]. Journal of East China University of Science and Technology, 2013, 32(1): 74-77. (in Chinese)
[3] 周群益,侯兆阳,刘让苏.Matlab可视化大学物理学[M].北京:清华大学出版社,2011.
[4] 马文蔚.物理学[M].北京:高等教育出版社,2006.
[5] 方云团.磁聚焦的图像和精度分析[J].物理与工程,2002,12(2):18-19. FANG Yuntuan. The figure and precision analysing of magnetic focusing[J]. Physics and Engineering, 2002,12(2): 18-19. (in Chinese)
[6] 周开红.带电粒子在喇叭形磁场中的运动分析[J].云南师范大学学报,2011,31(3):47-50. ZHOU Kaihong. Analysis on moving charged particles in the trumpet magnetic field[J]. Journal of Yunnan Normal University, 2011, 31(3): 47-50. (in Chinese)
[7] 史祥蓉,张景卓.带电粒子在非均匀磁场中运动的教学设计[J].物理与工程, 2014,24(3):31-33. SHI Xiangrong, ZHANG Jingzhuo. Instructional design of charged particle movementina non-uniform magnetic field[J]. Physics and Engineering, 2014, 24(3): 31-33. (in Chinese)
[8] 钟季康,鲍鸿吉.大学物理习题计算机解法—Matlab编程应用[M].北京:机械工业出版社,2008.
[9] 邝向军.带电粒子在典型非均匀磁场中的运动[J].陕西工学院学报,2004,20(4):63-65. KUANG Xiangjun. On the movement of electriferous particle in asymmetrical magnetic field[J]. Journal of Shaanxi Institute of Technology, 2004, 20(4): 63-65. (in Chinese)
[10] 雷前召.利用数值法改进大学物理课中的演示实验[J].渭南师范学院学报,2013,28(2):29-32. LEI Qianzhao. Using numerical methods to improve the demonstration experiments in the university physics[J]. Journal of Weinan Teachers College, 2013, 28(2): 29-32. (in Chinese)
[11] 刘建生,张流生,董太源.现代数值计算与模拟技术在大学物理中的应用[J].南方冶金学院学报,2004,25(5):45-49. LIU Jiansheng, ZHANG Liusheng, DONG Taiyuan. The application modern number calculation and simulating technique in university physics[J]. Journal of South Institute of Metallurgy, 2004, 25(5): 45-49. (in Chinese)
