预应力混凝土连续梁桥的摩阻系数研究①

周海涛， 赵 青， 陈宜强， 钟智强

(1.安徽建筑大学土木工程学院，安徽 合肥 230601；2.安徽金星预应力工程技术有限公司，安徽 合肥 231135)

0 引 言

在使用后张法进行预应力混凝土的施工时，其预应力损失中，摩阻损失是重要的一部分[1]，预应力摩阻损失由锚口、管道、喇叭口三种摩阻组成，其中管道的摩阻损失最大。对它的准确估计度将影响到对钢束施加的张拉力能否满足梁的使用要求和预拱变形。估计值太大会让钢束的张拉过度，从而导致梁端混凝土局部破损或开裂，并使得梁体延性下降；估计值过小会使预应力施加不足，从而导致桥梁的承载能力降低、出现裂缝或者变形等情况。预应力管道摩阻损失与管道的材料性质长度、力筋束种类等有关[2～3]，不同材料之间差异有大有小，最多能达到45%。在工程中对预应力管道摩阻损失用摩阻系数μ和管道偏差系数k来表示，虽然在设计规范中给出了对应材料其系数的取值范围，但为了工程质量得到更高的保证和施工控制的更加精确，并且在实际工程中，不同工程中其管道摩阻系数相差明显，所以，在对预应力进行张拉之前，需要对相同施工环境下的管道摩阻系数进行现场测定，从而可以为预应力张拉时所要施加的张拉力和伸长量提供依据，同时对施工过程中预拱度的控制提供帮助[4]。

1 工程概况

商合杭铁路安徽段特殊结构桥梁(40+56+40)m，采用悬臂现浇施工预应力单线连续梁，无声屏障，单座连续梁全长137.5m，桥梁顶面全宽7.4m，截面最低点梁高在端支座为2.8m，中支点为4.5m。选取6#墩 2号块F3(1×13-15.2-1860-GB/T5224-2003)和3号块F4(1×13-15.2-1860-GB/T5224-2003)，测试项目为金属波纹管管道摩阻系数测试。

2 试验原理

按照规范[5～6]预应力钢束的摩阻损失可按下式计算：

σl1=σcon[1-e-(μθ+kx)]

(1)

σcon为张拉端钢绞线锚下控制应力(MPa)

根据上式推算k和μ，设主动端压力传感器读数为P1,被动端为P2，管道长度为l，管道长的包角为θ，(1)式两边乘以钢束的有效面积，则可得：

P1-P2=P1(1-e-(μθ+kl))

(2)

即

P2=P1e-(μθ+kl)

(3)

将上式(3)两边取对数可得下式：

μθ+kl=-ln(P2/P1)

(4)

令y=-ln(P2/P1),可得

μθ+kl=y

(5)

在对不同管道测量时可得一系列方程组：

μθ1+kl1=y1即μθ1+kl1-y1=0

μθ2+kl2=y2即μθ2+kl2-y2=0

μθn+kln=yn即μθn+kln-yn=0

由于测试存在误差，令右边为误差值，假设

μθ1+kl1-y1=ΔF1μθ2+kl2-y2=ΔF2μθn+kln-yn=ΔFn

(6)

当

(7)

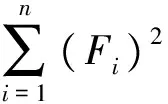
由式(6)、(7)可得：

(8)

式中：yi为第i管道对应的(-ln(P2/P1))值，li为第i个管道对应的预应力筋空间曲线长度(m)，θi为第i个管道对应的预应力筋空间曲线包角(rad)，n为实测的管道数目，且不同线形的预应力筋数目不小于2。解方程组(8)即可得出k及μ值。二元线性回归法是利用数理统计的计算方法，在试验中保证原始数据的稳定性与可靠性，在加上试验的数据越多，既可以得到更为准确的测试结果[7～8]。

3 试验内容

3.1 试验仪器设备

(1)2台穿心式液压千斤顶(2115,2117)、2台高压电动油泵(C22030717/ D01102317)、2块0.4级精密压力表。

(2)2台穿心式压力传感器(量程400t和650t)、2台数字应变仪(HZ-3)、2根对应的连接线。(如图1所示)

(3)对中工具。由现场条件进行确定。

(4)工具锚2套。

(5)0.5mm精度的钢尺1把，纸笔各2个，计算器1个。

图1 传感器及应变仪

图2 试验设备的安装示意图

图3 现场试验设备的安装

3.2 试验过程

为了是测试数据更加准确，试验使用了空心式压力传感器，通过读取主动端和被动端的压力来计算摩阻损失[9]。另外，为了使测试误差减小，将主动端和被动端交换张拉，安装示意图见图2。试验时仅主动端千斤顶进行张拉，被动端不张拉，进行试验三次，之后将主动端变被动端，被动端变主动端，主动端千斤顶进行张拉，被动端不张拉，再进行试验三次，每束力筋进行6次测试，然后取平均值。测试试验过程中对预应力钢束的张拉要保持连续均匀，防止预应力钢束收缩而引起测量误差[10]。钢束分4级加载，试验时根据千斤顶油表读数控制张拉荷载级，同时校对数据。安装传感器和千斤顶时，应保证两者中线位置与锚垫板在同一水平线上，使张拉时钢束与之减少摩擦[11～12]。现场安装如图3所示。

试验所用的F3，F4钢索的设计锚下张拉控制应力为1270MPa,对应的张拉力大小为P=2311 kN，试验最大张拉力为设计锚下张拉控制应力的100%。具体加载的荷载级情况见表1。最后计算出压力值，计算出孔道摩阻损失。

表1 具体加载的荷载分级情况

4 试验数据结果与分析

对试验梁的F3(1×13-15.2-1860-GB/T5224-2003)和F4(1×13-15.2-1860-GB/T5224-2003)管道进行测试。根据预应力钢束在各级荷载作用下张拉端至被动端的压力值计算有效系数A=F被/F张及其相应的Y=-lnA值。由施工图纸可得出其管道的曲线包角大小和预应力筋的曲线长度。其各预应力钢束管道摩阻测试数据及其对应的A值、Y值如表2所示，表中每级荷载张拉力均为6次张拉的有效张拉力的平均值。

表2 管道道摩阻试验记录表

表3 管道摩阻系数计算表

由表3数据在带入方程组(8)即可以得出k及μ值，结果见表4

表4 管道摩阻系数实测值

从表4可以看出实测的管道局部偏差系数和摩阻损失μ分别为0.0022、0.2441。这与设计值0.0025、0.2较为接近，差值影响在工程允许的范围以内。表明管道整体线形较为顺畅，满足设计要求。据此，在正式张拉时可以参考本次管道摩阻损失进行计算。μ的实测值略大于设计值，说明钢束的实际孔道摩阻损失比理论值要大，即实际张拉所施加的张拉力比设计值要小，原因主要是孔道成型不太好，施工过程中其位置产生了一定变形，还有就是在接口处存在一定的摩阻损失。

5 结 论

a)通过对试验结果的分析与研究表明上述的管道摩阻试验方法和原理是可行的 ，测得的k及μ值是可靠的，满足桥梁施工和监控的需求。

b)试验研究所得的实际数据与设计值偏差不大，说明管道摩阻系数在一般条件下是可以先依靠经验进行预估，为试验的研究提供一定参考，对于同一座桥梁来说，其不同截断的摩阻系数偏差不大。

c)摩阻系数的大小与管道的材料性质有关，本文研究的为金属波纹管的摩阻系数，对于其他类型的管道摩阻系数仍有待研究。

[1] 叶见曙.结构设计原理[M].北京:人民交通出版社,2005.

[2] 振春，孙桂云，赵迎萍.后张预应力混凝土梁管道摩阻及测试[J].西部探矿工程,2001(3):25- 27.

[3] 张伟雄.后张T梁预应力筋管道摩阻损失测试与分析[J].科技情报开发与经济,2001,11(1): 67-68.

[4] 洪拱辰.现代预应力混凝土结构[M].北京:中国建筑工业出版社,1988.

[5] TB10002.3-2005, 铁路桥涵钢筋混凝土和预应力混凝土结构设计规范[S].

[6] JTG D62-2004,公路钢筋混凝土及预应力混凝土桥涵设计规范[S].

[7] 杨欧峰，端茂军，魏洋,等.预应力混凝土连续梁桥管道摩阻试验研究及参数分析[J].中外公路，2016,36(4)：149-153.

[8] 张洪海，王金源. 铁路160m刚构预应力孔道摩阻试验分析[J].西部交通科技，2014(12)：64-70.

[9] 郑国庆,赵晓健,王卫锋.东江南特大桥预应力孔道摩阻损失试验研究[J].建筑监督检测与造价, 2009(08):10-12.

[10] 王涛,张汉平,钟穗东,等.桥梁预应力摩阻试验研究方法与研究.科学技术与工程，2009;9(19):5717-5720.

[11] 牛黎明.大跨度PC连续梁桥预应力管道摩阻研究[J].城市道路与防洪，2017(08)：90-92.

[12] 员宝珊，李登科，孙帅峰.乌准铁路 56 m 预应力连续箱梁管道摩阻试验研究[J].铁道建筑，2017(04)：32-34.