双圆弧斜齿齿轮泵脉动特性分析及齿形设计

李阁强 张龙飞 韩伟锋 邓效忠 冯 勇

1.河南科技大学机电工程学院，洛阳，471003 2.盾构及掘进技术国家重点实验室，郑州，450001 3.河南科技大学机械装备先进制造河南省协同创新中心，洛阳，471003

0 引言

针对渐开线齿轮泵存在的流量脉动大、噪声大、径向力不平衡等问题[1]，国内外学者提出了一些解决方案，如张静等[2]、杨国来等[3]采用斜齿代替直齿传动，宋爱平等[4]采用一种沿齿宽方向呈圆弧形状的齿形齿轮代替直齿传动，有效改善了流量脉动问题；刘元伟等[5]设计的单圆弧齿轮泵在理论上无脉动现象，但齿轮加工复杂，承载能力较低。力士乐公司的双圆弧斜齿轮泵噪声比普通齿轮泵平均降低11dB(A)，且流量与压力脉动远低于普通外啮合齿轮泵，与内啮合齿轮泵相当[6]。目前，对双圆弧斜齿齿轮泵的排量计算方法及流量脉动特性等尚无系统的理论分析，国内更没有相关产品。

笔者以双圆弧斜齿齿轮泵为对象，利用容积变化法推导出泵的理论排量计算公式，对比最大瞬时排量与最小排量得出其脉动特性，以正弦曲线为过渡曲线，依据齿轮共轭原理，得出双圆弧斜齿轮端面齿廓方程。

1 双圆弧斜齿轮及啮合原理

双圆弧齿轮是齿廓为圆弧形的点啮合齿轮，把两个单圆弧齿轮的凸凹齿廓组合在一个齿轮的齿廓上，即由两段圆弧加一定的过渡曲线构成。如图1所示，圆弧a1b1为齿顶圆弧，圆弧ba为齿根圆弧，两圆弧半径相同(为了避免齿轮在啮合过程中产生卡死现象及噪声，在实际制造中，齿根圆弧半径稍大于齿顶圆弧半径)，圆弧中心在节圆上。b1b为过渡曲线，与齿顶齿根圆弧分别相切于b1点和b点(过渡曲线可以是直线、抛物线、正弦线、余弦线等[7])。

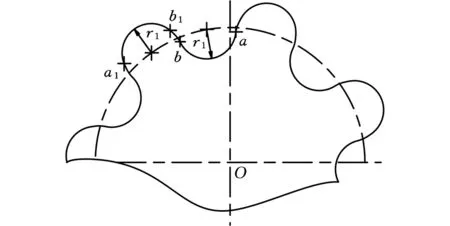
图1 双圆弧齿轮端面齿廓Fig.1 Transverse profile of double-circular-arc gear

双圆弧齿轮传动在同一个端截面中仅有一点接触，为了保证连续传动，必须做成斜齿，且两齿轮螺旋角大小相等、方向相反，轴向重合度大于1。双圆弧斜齿轮传动具有接触强度高、弯曲强度高、使用寿命长、加工工艺简单等优点[8]，因此，以双圆弧斜齿轮代替普通渐开线齿轮作为齿轮泵运动副，无论在平稳性、力矩还是在使用寿命方面，都比普通渐开线齿轮有很大优势。

较普通渐开线齿轮，双圆弧斜齿轮啮合重叠系数大，传动平稳，啮合为一点连续接触(在同一个端截面中仅有一点啮合，在不同端截面中各点依次啮合)，即在瞬时齿面可能同时存在两个接触点(图2中1、2两点)，所以作为泵，不会像渐开线齿轮泵那样产生困油现象。

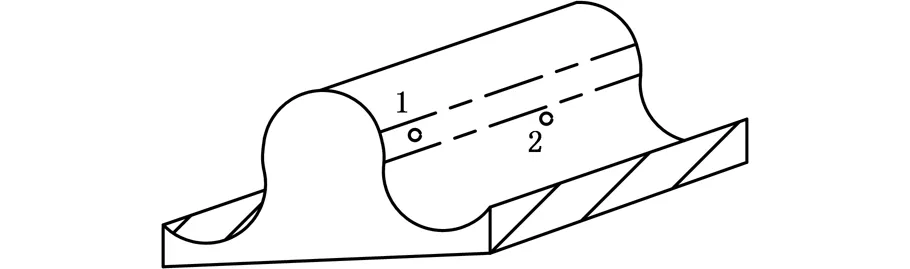
图2 双圆弧齿轮接触点分布Fig.2 Contact point distribution of double-circular-arc gear

如图3所示，双圆弧斜齿轮的啮合线为一条“8”字线，啮合过程中始终是凹面与凸面啮合，这与内啮合齿轮的啮合特征相同，齿面间的接触应力远小于凸面与凸面间的接触应力，相对滑动较小，因此寿命较长[9-10]。同时，一对双圆弧斜齿轮啮合过程中，齿顶与齿根也参与啮合，连续的齿面接触降低了工作噪声，恒定齿面接触几近以连续和无声的方式输送液压流体。

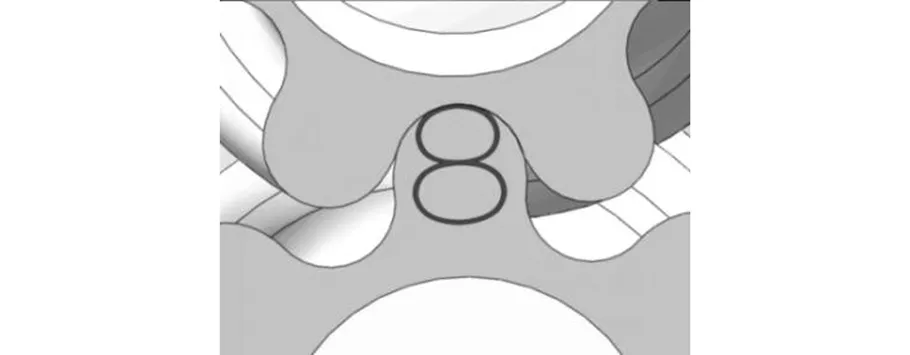
图3 双圆弧斜齿轮的啮合线Fig.3 Meshing lines of double-circular-arc helical gear

普通渐开线外啮合齿轮泵的齿轮重合度大于1，即在前一对齿轮尚未脱开啮合之前，后一对齿轮已经进入啮合，两对轮齿同时啮合时，它们之间形成一个与吸油腔、压油腔不相同的闭死容积，此即为困油现象，如图4a所示。双圆弧斜齿齿轮泵的齿轮啮合方式为一点连续式，端面重合度小于1，轴向重合度大于1，因此不会产生困油现象(图4b)，克服了困油现象造成的附加载荷，减小了机件的磨损、振动和噪声。

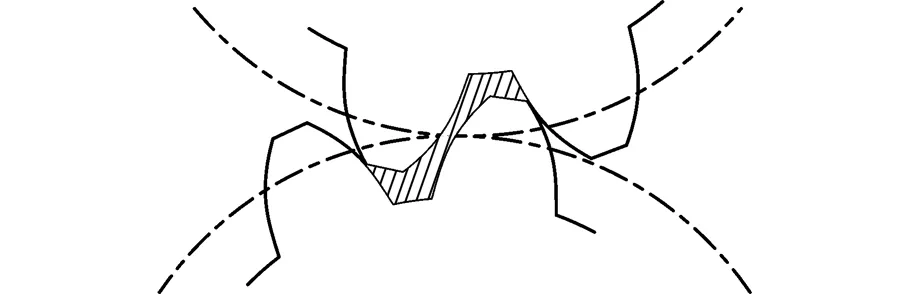
(a)渐开线齿轮

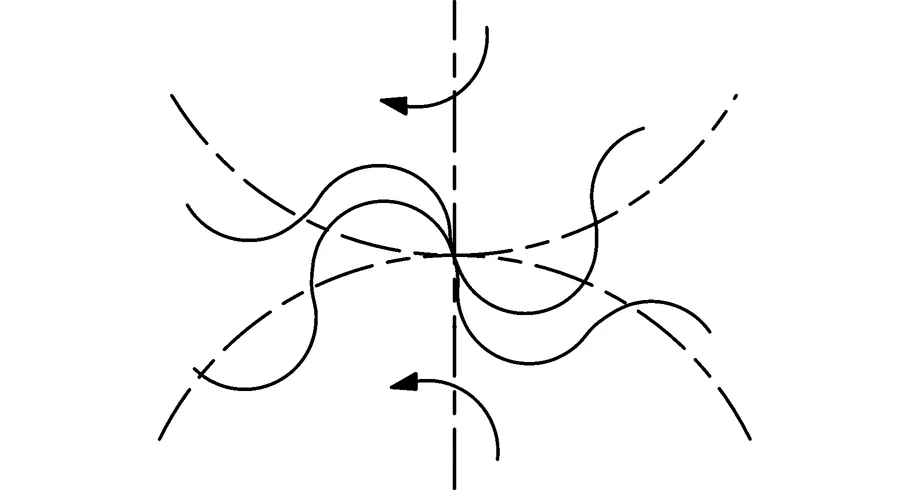
(b)双圆弧齿轮图4 双圆弧齿廓和渐开线齿廓比较示意图Fig.4 Sketch map of double circular arc tooth profile and involute tooth profile

2 双圆弧斜齿轮端面齿形设计

进行双圆弧斜齿轮齿廓设计，首先需确定过渡曲线形式[11]，过渡曲线有多种选择，以正弦曲线为过渡曲线的齿轮周节短、有效齿高大、输出排量大[12]。同时，选择较小的压力角，减小了轴承的载荷，为实现泵的高压化创造了条件。以正弦曲线为过渡曲线的端面齿廓方程设计如下。

如图5所示，节圆相同的主动轮O1和从动轮O2，过主动轮圆心O1作射线交主动轮节圆于s点，∠AO1P=β=π/(2z)(z为齿数)，任意设过A点的一条正弦曲线L为

(1)

式中，r为齿轮节圆半径；t为参变量；t0为初始值；s为过渡曲线到x轴最大坐标值的控制系数；n为控制正弦曲线周期的常数。

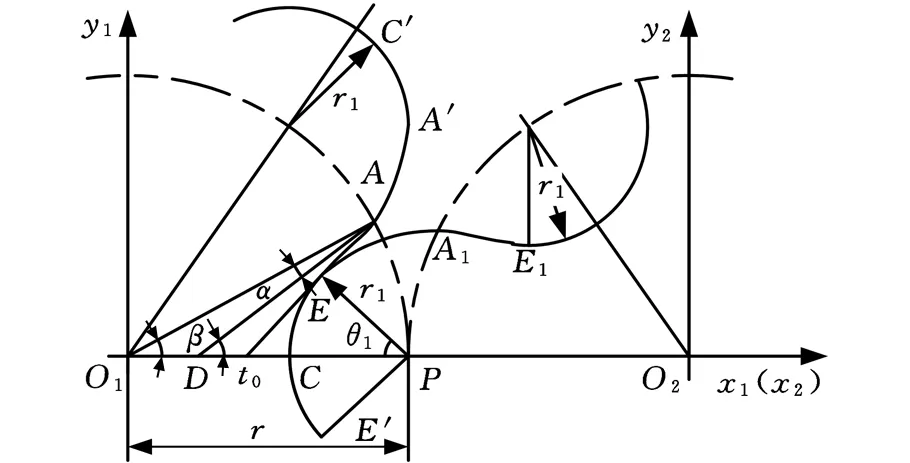
图5 双圆弧端面啮合分析图Fig.5 Double-circular-arc end face meshing analysis diagram

设过正弦曲线L上A点的切线与x轴交于点D，令A点压力角为α，由图5显见，∠ADP=β+α。

对于A点，有

(2)

式中，tA为A点变量参数t的值。

由式(2)可得

(3)

(4)

切线AD的斜率为

(5)

x1=1.5r即n(1.5-t0)=π/(2z)时，y有极大值，求得

(6)

将式(4)、式(6)代入式(5)可得

(7)

综上所述，在齿数z、压力角α已知的情况下，可解出n、tA、t0，即可得出正弦曲线L。

在正弦曲线L上任取一点E，令其法线过节点P(r,0)，则曲线E点的法线方程为

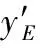
(8)

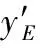
E点坐标分量为

(9)

式中，tE为E点变量参数t的值。

将式(2)、式(5)及P点坐标代入式(8)可得

(10)

如图5所示，以节点P为圆心，PE为半径作圆弧EE′，EE′为主动轮O1的齿根圆弧，亦为从动轮O2的齿顶圆弧。

由此可得，齿顶(根)圆弧半径r1为

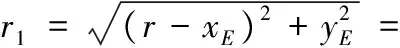
(11)

因r=mz/2，可令齿高系数

(12)

在齿轮泵齿轮副设计中，一般认为压力角为14.5°有利于减小轴承载荷、径向力，提高泵的综合性能。当压力角α=14.5°时，不同齿数z下tA、t0、n、tE、f1的值如表1所示。

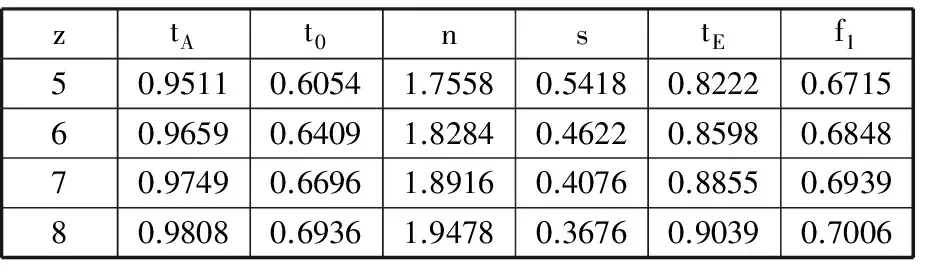
表1 齿形设计参数(α=14.5°)

确定齿轮O1上的一段曲线方程后，可通过齿轮啮合共轭原理[13-16]求得齿轮O2与之相共轭的一段曲线方程，亦可通过齿轮O2上的一段曲线方程得到齿轮O1上的曲线方程，具体求解如下。

如图6a所示，坐标系S1(O1x1y1z1)、S2(O2x2y2z2)是两齿轮啮合传动空间固定坐标系，z1轴与z2轴分别与两齿轮轴线重合。x1轴与x2轴重合，它们的方向即为两轴的最短距离方向，它们之间的距离即为中心距2r。

坐标系Sm(O1xmymz1)、Sn(O2xnynz2)分别是与两齿轮固连的坐标系，在起始位置时，它们分别与坐标系S1、S2重合。齿轮分别绕z1轴、z2轴转动，经过一段时间后，坐标系Sm(O1xmymz1)、Sn(O2xnynz2)运动到图6a所示位置时，齿轮对应转角为θ，根据图中所示坐标关系可以得到由坐标系Sm(O1xmymz1)变换到Sn(O2xnynz2)的坐标变换矩阵：

(13)

在平面坐标系O1x1y1中，曲线EA1是曲线EA共轭运动中展成的一段共轭曲线，它在平面坐标系O2x2y2中的方程可通过坐标矩阵Mnm得到：

(14)

将曲线EA1方程代入式(14)可得

(15)

同理，如图6b所示，齿轮继续分别绕z1轴、z2轴转动，经过一段时间后，固连坐标系运动到Sm(O2xmymz2)、Sn(O1xnynz1)时，齿轮对应转角为θ+β，根据图中所示坐标关系可得曲线AA′在平面坐标系x1O1y1中的方程：

(16)

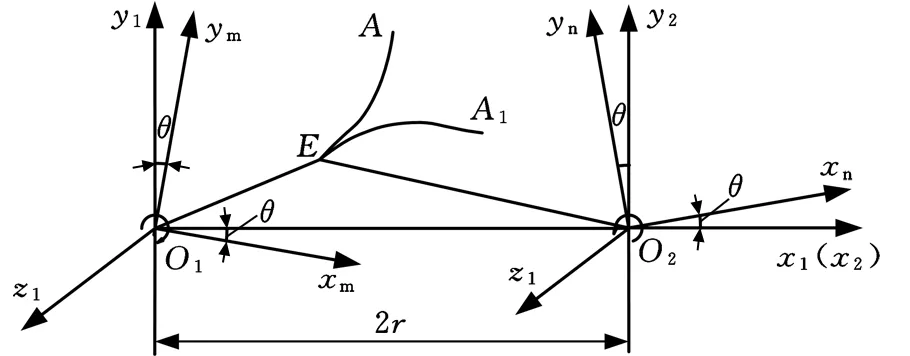
(a)齿轮转角为θ

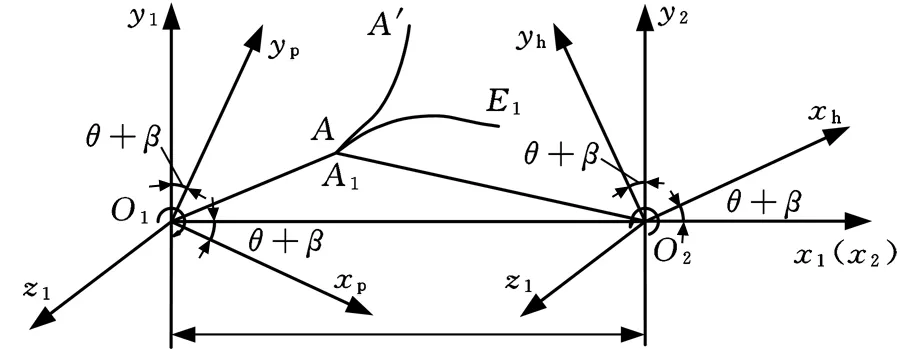
(b)齿轮转角为θ+β图6 双圆弧斜齿轮啮合传动空间坐标系Fig.6 Spatial coordinate system of double circular helical gear meshing drive

在平面坐标系O1x1y1中，曲线上E点的法线过节点P，PE为齿根圆弧半径，设齿根圆弧CE的方程为

(17)

通过坐标变换以及啮合原理，可得平面坐标系O1x1y1中齿顶圆弧AA′的方程：

(18)

啮合线是齿轮齿面上的理论接触点在固定坐标系中的集合，所以将理论接触点在动坐标系中的坐标转换到固定坐标系中的坐标值即可求出啮合线方程式，故PE部分的啮合线方程可通过坐标变换得到：

(19)

至此，通过坐标变换以及啮合原理，完成了以正弦曲线为过渡曲线的双圆弧斜齿齿轮泵的端面齿廓方程的求解。

3 双圆弧斜齿齿轮泵排量计算及脉动分析

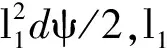
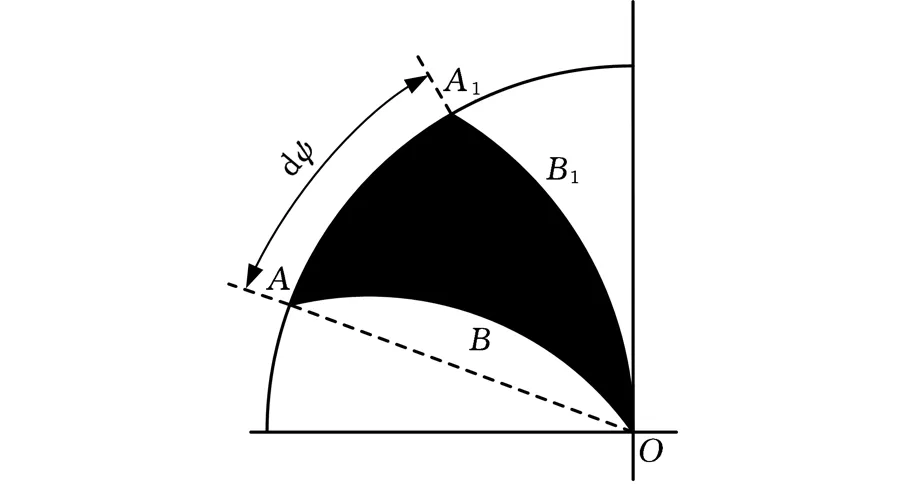
图7 曲线ABO旋转扫过的面积Fig.7 Area of curve ABO rotation swept

如图8所示，当齿轮转动ξ角度即由图示实线啮合状态转动至虚线啮合状态时，双圆弧齿轮泵的容积变化为

V=V1+V2-V3+V4

式中，V1为ΔO1A11A12的对应容积；V2为ΔO2A21A22的对应容积；V3为梯形O1B1B2O2的对应容积；V4为梯形O1C1C2O2的对应容积。

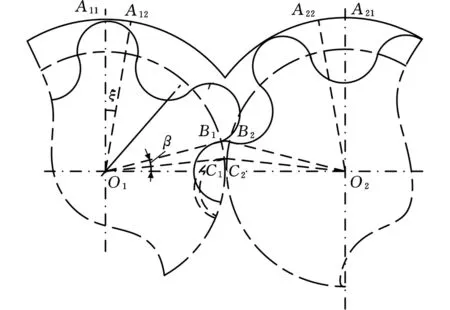
图8 双圆弧直齿齿轮泵啮合分析图Fig.8 Meshing analysis diagram of double circular arc straight gear pump

可得压油腔排出的容积：

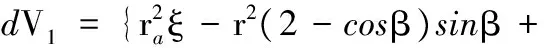
(20)

式中，R为双圆弧齿轮节圆半径，R=(a+Δa)/2；a为齿轮中心距；Δa为齿轮中心距误差；ra为齿轮齿顶半径；ξ为齿轮转角；β为双圆弧直齿轮1/4周节所对应的弧度。

由β=π/(2z)可得齿轮转动角度ξ时，压油腔排出的容积：

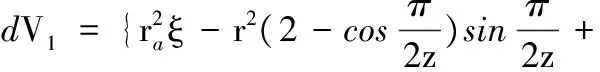
(21)

压油腔压出的液体瞬时流量为

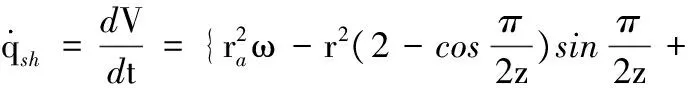
(22)

式中，ω为齿轮转角ξ所对应的角速度。

对微元薄齿x进行积分可得泵的瞬时流量

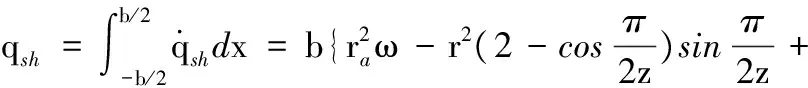
(23)

式中，b为齿宽。

泵旋转一周的排量为

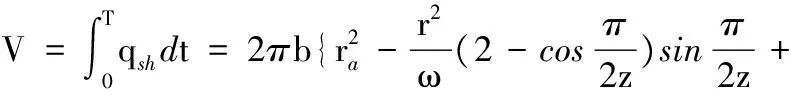
(24)

式中，T为齿轮转一周所需要的时间，T=2π/ω。

双圆弧斜齿轮可视为由无数个无限薄的双圆弧直齿轮连续转过1个相位角叠加而成，其流量输出特性可由距基准面为任意距离无限薄的双圆弧直齿轮的流量特性通过积分得到。距基面x处(沿齿宽方向)啮合点所对应的转角为

(25)

式中，β0为双圆弧斜齿轮螺旋角；φ1为齿轮端面转角。

厚度为dx的双圆弧斜齿轮泵的瞬时排量为

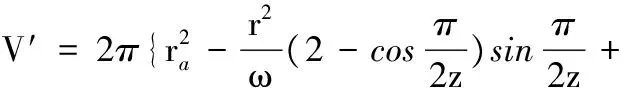
(26)

式(26)是一个以2Nπ/z(N为正整数)为周期的连续函数，且在一个周期内，函数左右对称，所以只需要考虑在[-π/z,π/z]内的函数变化即可得到整个区间上的函数特性，即输出流量的脉动特性。

如图9所示，齿宽为b处的波形比齿宽为零处的波形超前一个相位角(btanβ0)/r，假设F点坐标为-π/z，B点坐标为-π/z，则D点坐标为π/z-(btanβ0)/r，假设齿宽为零处的波形在第N-1个周期，则齿宽为b处就存在第N-1和第N个周期的波形，由于不同周期内的波形表达式不同，故应该分为两个区间分别进行讨论。

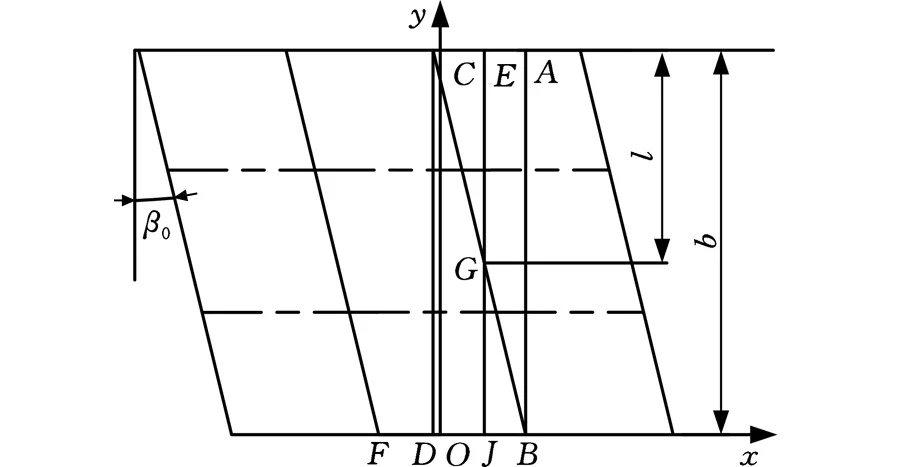
图9 双圆弧斜齿轮泵输出瞬时排量示意图Fig.9 Output instantaneous displacement of double circular arc helical gear pump

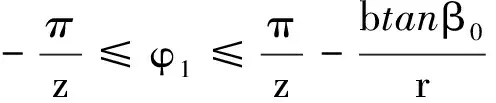
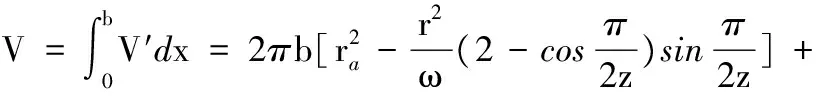
(27)

令dV/dφ1=0，可得

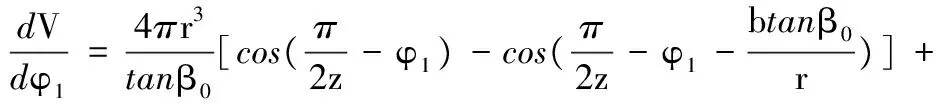
(28)

(29)

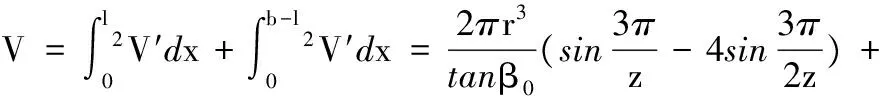
(30)

令dV/dl2=0，可得

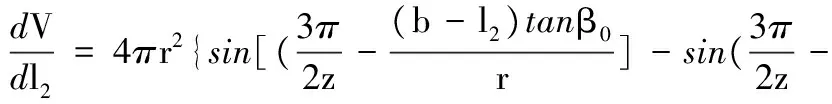
(31)

由此可得，当l2=b/2时，该函数有极小值。

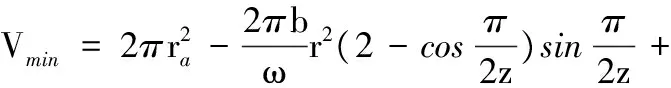
(32)

通过上述分析计算可得双圆弧斜齿齿轮泵排量的最大值与最小值，由最大值和最小值的差即可得到该泵的脉动特性：

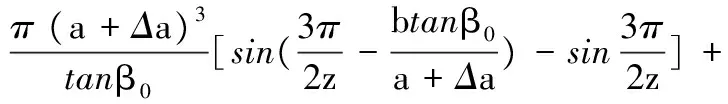
(33)

由式(33)可知，理论上双圆弧斜齿齿轮泵的流量脉动趋于零。

4 流量脉动仿真分析

为验证流量脉动理论计算的正确性，假定双圆弧斜齿轮端面模数m=7.5 mm，齿数z=7，齿宽b=45 mm，压力角α=14.5°，螺旋角β0=28°，可得齿顶、齿根圆弧半径r1=f1m=5.204 mm，节圆直径r=mz=52.5 mm，齿顶圆直径Da=D+2r1=115.408 mm，齿根圆直径Db=D-2r1=94.592 mm，D为节圆直径。双圆弧斜齿齿轮泵的简易模型如图10所示。采用有限元软件ANSYS/Workbench中的前处理模块(ICEM)、分析计算模块(Fluent)，并结合三维动网格技术，对比分析齿轮参数相同的双圆弧斜齿轮泵和普通渐开线斜齿轮泵的流量脉动。

图10 双圆弧斜齿齿轮泵简易模型Fig.10 Simple model of double circular arc helical gear pump

应用ICEM对双圆弧斜齿轮泵的流体域进行网格划分；由于齿轮泵中左右齿轮啮合旋转，即流动要素是随时间发生变化的，因此采用非定常流动(Transient)模块描述其流动特性；由于尺寸旋转较大将导致较大的逆压力梯度，所以采用Models节点中的Realizable k-epsilon湍流模型；定义进出口边界类型分别为pressure-inlet、pressure-outlet，设置进口总压力为0，出口总压力为25 MPa，设置湍流方式为Intensity and Viscosity Ratio，湍流强度为5%，湍流黏度比为5。动网格采用弹簧光顺法(Smoothing)以及局部网格重构法(Remeshing)。设置网格重构方法为local cell和local face，重构频率参数为1；齿轮泵的流量脉动仿真只有左右两个齿轮啮合旋转，因此可采用运动函数文件(profiles)定义两个齿轮旋转；定义左右齿轮为刚体运动，齿轮上下壁面为变形区域，设置变形体型为Plane(设置区域节点只能在该平面上移动)。

在Monitors节点下设置Surface Monitors，以定义齿轮泵出口流量监视器，采用Hybrid Initialization方法初始化，设置时间步长为5×10-6s，迭代次数为3000，内迭代次数为40，计算后可得双圆弧斜齿轮泵流量监测曲线,如图11所示，Y轴代表负值方向，表示流体流出计算域。由图11可以看出，在开始阶段，两种齿形齿轮泵流量持续增大，随后输出流量呈现出周期波动，波动间隔为齿轮泵的旋转周期，可明显看出双圆弧斜齿轮泵的流量脉动远小于普通渐开线斜齿轮泵的流量脉动。

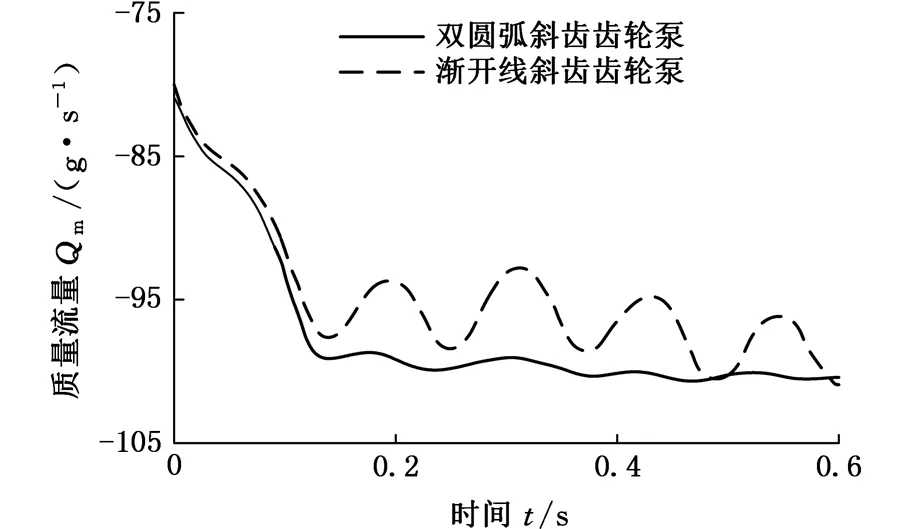
图11 齿轮泵流量监测曲线Fig.11 Flow monitoring curve of gear pump

5 结论

(1)提出将双圆弧斜齿轮作为齿轮泵的运动副，并证明其可以有效解决普通渐开线外啮合直齿齿轮泵流量脉动大、噪声大、困油现象严重等问题。

(2)采用正弦曲线为过渡曲线进行齿形设计，具有较大的有效齿高，同时可选择较小的压力角，达到了增大输出排量、减小轴向载荷，以达到高压化的目的。

(3)利用齿轮啮合共轭原理给出了双圆弧斜齿轮的端面齿廓方程设计方法，为实现齿轮泵的高性能提供了一种解决方案。

(4)采用有限元软件ANSYS/Workbench，结合三维动网格技术，对比分析齿轮参数相同的双圆弧斜齿轮泵和普通渐开线斜齿轮泵的流量脉动，得出双圆弧斜齿轮泵的流量脉动远小于渐开线斜齿轮泵的流量脉动。

[1] EMILIANO M, GIORGIO D, ALESSANDRO R. Dynamic Behavior of Gear Pumps: Effect of Variations in Operational and Design Parameters[J]. Meccanica 2011, 46(6): 1191-1212.

[2] 张静, 史伟东, 胡亮.斜齿轮泵流量及其流量脉动特性分析[J]. 液压气动与密封, 2016, 36(6): 8-12.

ZHANG Jing, SHI Weidong, HU Liang. The Characteristic Analysis on Flow Rate and Flow Pulsation of Helical Gear Pump[J]. Hydraulics Pneumatics & Seals, 2016, 36(6): 8-12.

[3] 杨国来, 张晓丽, 李文祺. 基于MATLAB的渐开线外啮合斜齿轮泵流量脉动特性的仿真[J]. 液压与气动, 2015 (2): 55-58.

YANG Guolai, ZHANG Xiaoli, LI Wenqi. MATLAB-based Flow Pulsation Characteristic Simulation for Involute Meshing External Helical Gear Pump[J]. Chinese Hydraulics & Pneumatics, 2015 (2): 55-58.

[4] 宋爱平, 周骥平, 吴伟伟，等. 弧齿齿轮泵瞬间流量及其脉动特性研究[J]. 中国机械工程, 2009, 20(19): 2315-2319.

SONG Aiping, ZHOU Jiping, WU Weiwei, et al. Research on Instant Flow Characteristic and Pulsation of Arch Gear Pump[J]. China Mechanical Engineering, 2009, 20(19): 2315-2319.

[5] 刘元伟, 崔光宇. 单圆弧齿轮泵输出特性分析[J]. 大连交通大学学报, 2008,29(4): 45-47.

LIU Yuanwei, CUI Guangyu. Analysis of Single Arc Gear Pump for Flow Output Property[J]. Journal of Dalian Jiaotong University, 2008, 29(4): 45-47.

[6] 张海平. 德国汉诺威2011展会观摩报告[J]. 液压气动与密封, 2011, 31(6): 5-9.

ZHANG Haiping. Report about Hannover Messe[J]. Hydraulics Pneumatics & Seals, 2011, 31(6): 5-9.

[7] LIU Yuanwei, FAN Jia. Design of Asymmetric Double Circular Arc Gear for Large-scale High-Pressure Gear Pumps[J]. Advanced Materials Research. 2011, 181/182: 361-365.

[8] 张国贤. 外啮合圆弧齿轮泵[J], 流体传动与控制, 2012 (1): 53-55.

ZHANG Guoxian. Outer Meshing Circular Arc Gear Pump[J], Fluid Power Transmission and Control, 2012(1): 53-55.

[9] ZHOU Yang, HAO Shuanghui, HAO Minghui. Design and Performance Analysis of a Circular-arc Gear Pump Operating at High Pressure and High Speed[J]. Journal of Mechanical Engineering Science, 2016, 230(2): 189-205.

[10] LIU Yuanwei, FAN Jia. Study of Tooth Profile Design with Asymmetric Double Circular Arc Gears for Pumps[J], Applied Mechanics & Materials. 2010, 43: 409-413.

[11] 徐文博,刘世军,李志胜. 双圆弧齿轮的精确建模与动态接触分析[J]. 机械传动, 2013, 37(1): 68-70.

XU Wenbo, LIU Shijun, LI Zhisheng. Research on Accurate Modeling and Dynamic Contact Analysis of Double Circular Arc Gear[J]. Mechanical Transmission, 2013, 37(1): 68-70.

[12] 周洋. 高性能圆弧齿轮泵关键技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2016.

ZHOU Yang. Research on the Key Technologies of High Performance Circular Arc Gear Pump[D]. Harbin: Harbin Institute of Technology, 2016.

[13] 陈兵奎, 梁栋, 高艳娥. 齿轮传动共轭曲线原理[J]. 机械工程学报, 2014, 50(1): 130-136.

CHEN Bingkui, LIANG Dong, GAO Yane. The Principleof Conjugate Curves for Gear Transmission[J]. Journal of Mechanical Engineering. 2014, 50(1): 130-136.

[14] CHEN C K, YANG S C. Geometric Modelling for Cylindrical and Helical Gear Pumps with Circular Arc Teeth[J]. Journal of Mechanical Engineering Science, 2000, 214(4): 599-607.

[15] 陈兵奎, 李海翔. 渐开弧面齿轮的形成原理与数学模型[J]. 机械工程学报, 2012, 48(3): 57-62.

CHEN Bingkui, LI Haixiang. Generation Principle and Mathematical Models of Involute-circular Gear[J]. Journal of Mechanical Engineering. 2012, 48(3): 57-62.

[16] 唐进元, 周炜, 陈思雨. 齿轮传动啮合接触冲击分析[J]. 机械工程学报, 2011, 47(7): 22-30.

TANG Jinyuan, ZHOU Wei, CHEN Siyu. Contact-impact Analysis of Gear Transmission System[J]. Journal of Mechanical Engineering， 2011, 47(7): 22-30.