刚柔耦合柔性机械手二阶理论精准建模及实验研究

赵 燕 阮成明 王松伟

武汉理工大学机电工程学院，武汉，430070

0 引言

柔性机械手动力学行为表现为复杂的刚柔耦合现象[1-2]，其动力学模型具有时变、非线性、强耦合等特点，而模型的建立是对柔性机械手进行动力学研究分析的基础。

目前，在柔性机械手理论建模的动边界条件及变形理论方面均取得了一定的研究成果。描述柔性臂弹性变形主要有三种理论：经典变形理论、综合变形理论、二次变形理论。DE LUCA使用经典变形理论进行单关节柔性机械手的建模，并用模型设计了一个理想的控制器。ABE[3]为了减小残余振动，采用二次变形理论进行最优轨迹的设计，所设计的最优轨迹能够有效抑制柔性机械手的残余振动。在柔性臂动边界理论方面，刘建英等[4]将柔性机械手视为包含边界条件的悬臂梁和简支-自由梁模型，采用假设模态法建立柔性臂的动力学模型并进行柔性欠驱动机械臂的动力学耦合分析。相对于传统建模方法，精准建模的精准性主要体现在三个方面：①传统建模一般选择1阶线性简化模型，精准建模选择2阶非线性复杂模型；②传统建模认为实验的动边界条件就是悬臂边界条件，精准建模认为实验的动边界条件是4种边界条件的耦合；③传统建模选用经典变形理论来建立动力学方程，精准建模考虑3种变形理论。

柔性机械系统的建模方法主要有假想模态法、有限元法和集中质量法。假想模态法、有限元法建立的模型只能做定量分析，不能做系统的参数化分析；集中质量法是一种近似考虑方法。本文从理论建模和实验验证两个方面展开，选取Euler-Bernoulli梁模型，结合假想模态法与拉格朗日法建立柔性臂的动力学模型。通过实验验证柔性臂的模态频率，找出和实际工况更贴近的理论模型。

1 双关节柔性机械手的精准建模

1.1 柔性梁的型函数

双关节柔性机械手是由刚性关节和柔性关节组成的复杂刚柔耦合机械手系统。动力学建模的精准性受型函数类型的影响[5]，而型函数选择和动边界条件又有密切的联系[6-7]，下面首先建立不同动边界条件下的型函数。

均匀材料等截面梁的弯曲自由振动方程为

(1)

式中，ρ为材料密度；A为横截面积；E为材料的弹性模量；I为机械手的截面惯性矩；w(x，t)是柔性机械手在任一点x上所对应的变形量。

本文采用假想模态法进行理论建模，即将每一阶模态表示成模态坐标和模态型函数的乘积，将连续几阶模态相加就得到整个柔性机械手上任意一点的振动量：

(2)

式中，Wi(x)为型函数；qi(x)为Wi(x)对应的模态坐标。

(3)

λ的数学表达式为

(4)

式中，f为自然频率;l为柔性机械手的长度。

柔性机械手的动边界条件如图1所示，其中，D、S、M、Q分别为挠度、转角、弯矩和剪力。

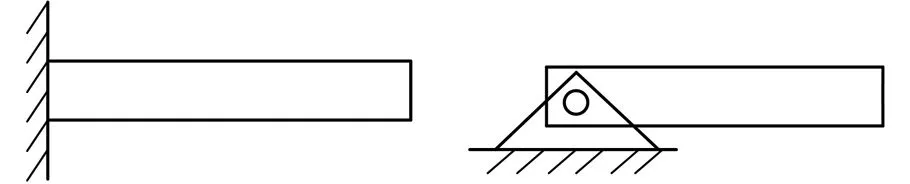
(a)固定-自由D=0,S=0;M=0,Q=0(b)铰接-自由D=0,M=0;M=0,Q=0

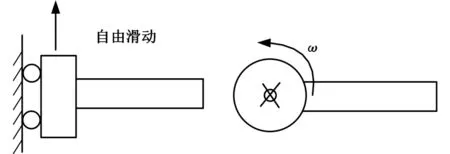
(c)滑动-自由S=0,Q=0;M=0,Q=0(d)转动-自由S=0,M=0;M=0,Q=0图1 4种边界条件Fig.1 Four boundary conditions

将以上4种动边界的位移、转角、弯矩和剪力进行统计并列入表1。

表1 梁的4种边界条件

表2 4种边界条件对应的型函数

根据表2所示的型函数，由牛顿-二分法可以求解出表3所示的3种梁模型前两阶模态的相关参数，其中，ωi为角频率、Wi(l)为柔性臂末端的型函数值。在图1c、图1d所示的边界条件下，特征值λi存在为零的情况，所以频率方程有零根即ω0=0，对应柔性机械手在这两种边界条件的刚体运动。

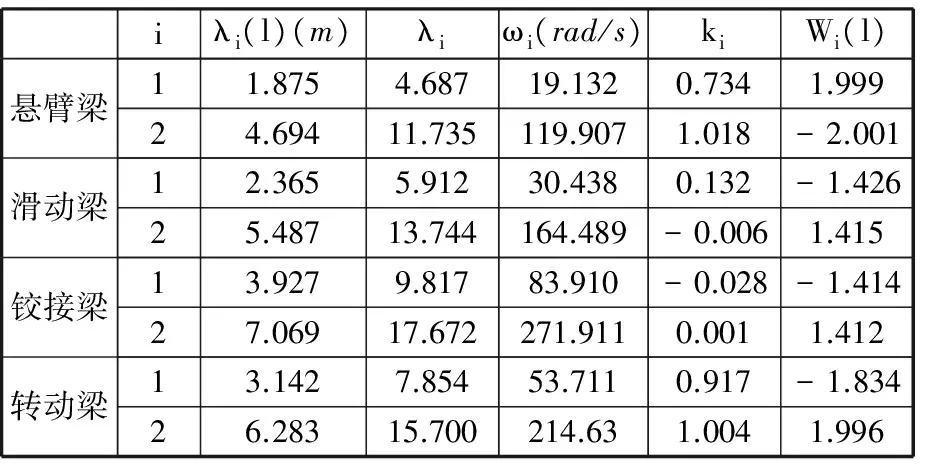
表3 柔性机械手模态参量值

1.2 双关节柔性机械手动力学方程的建立

模型由柔性臂、刚性臂、刚性基座、柔性基座组成。OXY坐标系是固定于平面的惯性参考坐标系；oxy是固定于柔性机械手基座的局部坐标系，会随着柔性机械手基座的转动而转动。3种变形理论下的坐标原理图分别为图2～图4。经典变形中，任意点的变形w(x，t)垂直于局部坐标系的x轴，如图2所示；综合变形当中，变形量w(x，t)垂直于位置矢量r，如图3所示；二次变形理论较经典变形理论，唯一不同的是在二次变形中考虑柔性机械手的轴向伸长量u，如图4所示。

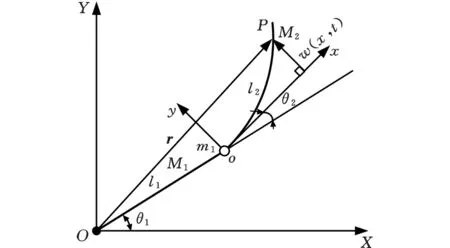
图2 经典变形Fig.2 Classical deformation

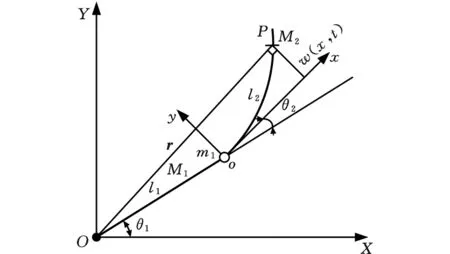
图3 综合变形Fig.3 Comprehensive deformation

图4 二次变形Fig.4 Secondary deformation

选用广义坐标来确定系统的空间坐标位置，用拉格朗日方程来描述物体的运动规律。双关节柔性机械手的动能包括柔性臂、刚性梁、刚性梁末端电机等三部分的动能，具体表达式为

(5)

式中，J1为刚性梁绕基座上转轴的转动惯量；J2为柔性梁绕基座上转轴的转动惯量；θ1、θ2分别为杆1和杆2的刚性旋转角度；m1为刚性梁末端电机的质量；r为柔性臂任意点的位置矢量。

本文所研究的柔性机械手在水平面内转动，可忽略重力影响，故柔性机械手的势能只包含弹性势能[8]：

(6)

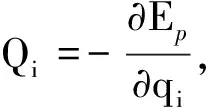
(7)

i=1,2,…,n

得到系统的拉格朗日动力学方程：

(8)

式中，qi为模态坐标，i=1,2。

这里取前二阶模态w(x,t)=W1(x)q1(t)+W2(x)q2(t)。

1.2.1双关节柔性机械手经典变形

根据图2可得r在全局坐标系的表达式：

(9)

θ=θ1+θ2

对位置矢量r求导就可以得到相应的速度分量：

(10)

将式(9)、式(10)代入式(5)、式(6)整理化简，再将化简后的结果代入式(8)，得到经典变形下双关节柔性机械手的拉格朗日动力学方程：

(11)

1.2.2双关节柔性机械手的综合变形

根据图3可得r在全局坐标系的表达式：

(12)

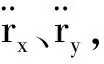
(13)

1.2.3双关节柔性机械手二次变形

根据图4可得r在全局坐标系的表达式：

(14)

(15)

(16)

(17)

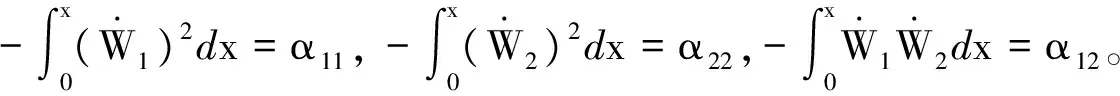
1.3 理论计算及仿真

为了确定不同边界条件和变形理论对建模精准性的影响就要进行理论求解和仿真。研究中选用梁的基本参数如下：梁厚度b=0.2 mm，梁长度L=40 mm，密度ρ=7.7×103kg/m3，横截面积A=1.85×10-5m2，弹性模量E=200 GPa，中性轴惯性矩I=5.4×10-13m4。电机的输入轨迹为

(18)

这里以悬臂梁为例计算出经典变形理论下的拉格朗日动力学方程，并利用MATLAB求解柔性机械手末端的振动位移。由表2、表3可知，一端固定、一端自由的悬臂梁的前两阶型函数分别为

W1(x)=cosh4.688x-cos4.688x-
0.734(sinh4.688x-sin4.688x)

(19)

W2(x)=cosh11.735x-cos11.735x-
1.019(sinh11.735x-sin11.735x)

(20)

将以上型函数以及模型参数代入式(11)，得到经典变形理论下的理论模型：

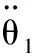
(21)

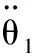
(22)

运用MATLAB龙格-库塔函数求出对应的模态坐标q1、q2，通过公式w(x,t)=W1(x)q1(t)+W2(x)q2(t)可以计算出双关节柔性机械手末端振动位移并得到其随时间变化的振动位移-时间图。同理可得到悬臂梁在二次变形理论和综合变形理论下的振动位移-时间图。结合滑动梁、铰接梁、转动自由梁这3种动边界条件下的型函数，按照上述方法亦可求出双关节柔性机械手在另外3种动边界条件下分别对应不同变形理论时的振动位移-时间曲线，如图5～图8所示。从横向(动边界条件固定对应不同变形理论)和纵向(变形理论固定对应不同变形理论)两个角度对理论计算结果进行分析。

图5 悬臂梁末端振动位移Fig.5 Vibration displacement at the end of a cantilever beam

图6 滑动梁末端振动位移Fig.6 Vibration displacement at the end of sliding beams

图7 铰接梁末端振动位移Fig.7 Vibration displacement at the end of articulated beams

图8 转动梁末端振动位移Fig.8 Vibration displacement at the end of rotating beams

横向分析，动边界条件固定时，不同的变形理论对柔性机械手末端的边缘振动位移影响十分的微小，这说明，动边界一定的前提下，在低速(电机停止时,柔性机械手的转动速度小于柔性机械手的一阶固有角频率)范围内，3种变形理论对于建模精准性有一定的影响，但是这种影响可以忽略不计。纵向分析，4种动边界条件对柔性机械手的末端边缘振动位移影响较大，不同边界条件下柔性机械手边缘振动的位移(从大到小)为：悬臂条件、滑动条件、转动条件、交接条件。此外，动边界条件对柔性机械手边缘振动位移的模态频率也有较大的影响。

2 双关节柔性机械手的模型验证实验

从1.3节的结果分析得知，3种变形理论对理论模型的影响比较小。由于实验设备局限性,这里只对模型动边界条件进行验证。

2.1 实验目的

双关节柔性机械手工作时的边界条件是一种复杂的耦合状态。因此实验研究的目的是通过对比分析确定哪一种柔性机械手模型与实际工作状况更为贴近。

2.2 双关节柔性机械手实验测量的基本原理

如图9所示，利用PC机设定电机的输入轨迹，电机驱动柔性机械手在1 s内转动π/2后停止转动，电机停止转动后双关节柔性机械手开始自由振动。通过粘贴在柔性机械手上的电阻应变片测出柔性机械手自由振动的应变桥压信号，应变桥压信号经过放大和滤波可以得到柔性机械手自由振动末端应变(包括优化前应变、优化后应变、HySMC优化后的应变)。实验装置如图10所示。

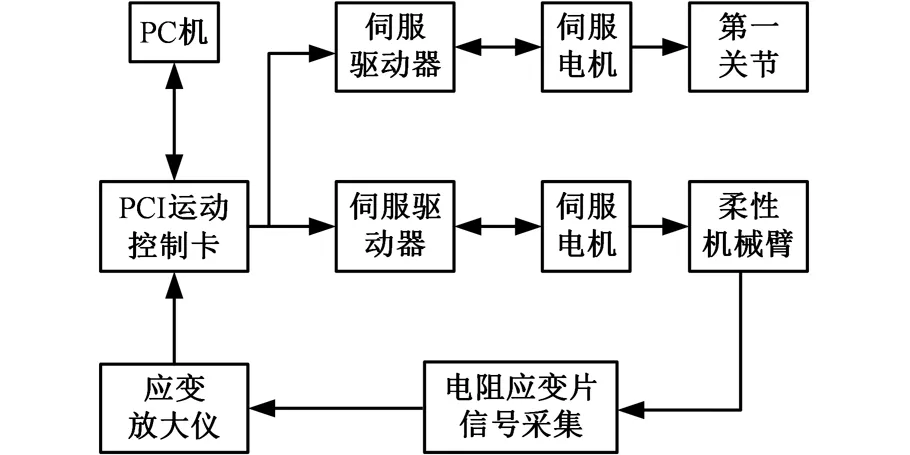
图9 双关节柔性机械手的实验测量原理框图Fig.9 Experimental measurement block diagram of biaxial joint flexible manipulator

图10 双关节柔性机械手的实物连接图Fig.10 The connection diagram of the biaxial flexible manipulator

2.3 实验结果分析

图11是实验条件下测得的双关节柔性机械手自由振动的应变-时间图。本文从模态频率角度来对比验证理论模型的正确性，为了方便和理论计算结果进行比较这里取一阶模态。柔性机械手的模态频率就是柔性机械手在1 s内的振动次数。通过图11，可以计算出在1 s 内柔性机械手末端自由振动的次数接近8.5即频率为8.5 Hz。结合表3的模态角频率参数和公式ωi=2πfi可求出不同边界条件下的模态频率，对比实验结果如表4所示。

图11 双关节柔性机械手的应变-时间图Fig.11 Strain-time diagram of flexible manipulator with biaxial joints

悬臂梁滑动梁铰接梁转动梁实验结果fi(Hz)3．054．8513．368．558．5

从表4可以看出，双关节柔性机械手的实验结果最接近于转动自由梁动边界条件下的理论建模计算值。

3 结论

(1)基于3种变形理论和4种动边界条件建立了双关节柔性机械手的动力学模型，通过理论计算分析发现3种变形理论对双关节柔性机械手理论建模精准性影响较小，动边界条件对双关节柔性机械手理论建模精确性影响较大。

(2)通过实验对比了双关节柔性机械手在不同动边界理论模型和实验条件下的模态频率，发现实验结果和转动-自由边界条件下的理论建模仿真值最吻合，从而得出如下结论：转动自由梁模型与实际工作状况更为贴近，其适用于双关节柔性机械手的理论建模。

[1] 谷勇霞，张玉玲，赵杰亮，等, 柔性机械手动力学建模理论与实验研究进展[J]. 中国机械工程, 2016,

27(12): 1694-1703.

GU Yongxia, ZHANG Yuling, ZHAO Jieliang, et al. Advances on Dynamics Modeling and Experimental Studies for Flexible Manipulators[J].China Mechanical Engineering, 2016, 27(12): 1694-1703.

[2] 褚明.空间柔性机械手动力学特性与主动控制研究[D].北京：北京邮电大学，2010.

CHU Ming. Research on Dynamic Characteristics and Active Control of Space Flexible Manipulator[D]. Beijing: Beijing University of Posts and Telecommunications, 2010.

[3] ABE A.Trajectory Planning for Residual Vibration Suppression of a Two-link Rigid-flexible Manipulator Considering Large Deformation[J]. Mechanism and Machine Theory,2009, 44(12): 1627-1639.

[4] 刘建英，王校岳，宫金良.柔性欠驱动机械臂动力学耦合分析[J].中国机械工程，2017,28(22):2732-2746.

LIU Jianying, WANG Xiaoyue, GONG Jinliang. Dynamics Coupling Analysis of Flexible Underactuated Manipulators[J].China Mechanical Engineering,2017,28(22):2732-2746.

[5] DWIVEDY S K, EBERHARD P. Dynamic Analysis of Flexible Manipulators[J]. Mechanism and Machine Theory， 2006,44(12) :749-777.

[6] LI S，LIU H. Vibration Analysis on Complex Boundaries Model of Aero-engine’s Vane[J]. Machine Design & Research, 2008, 24(6): 60-63.

[7] 章孝顺,章定国,洪嘉振.考虑曲率纵向变形效应的大变形柔性梁刚柔耦合动力学建模与仿真[J].力学学报, 2016,48(3): 692-701.

ZHANG Xiaoshun, ZHANG Dingguo, HONG Jiazhen. Rigid and Flexible Coupling Dynamic Modeling and Simulation of a Large Deformed Flexible Beam Considering Curvature Longitudinal Deformation Effect[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016,48(3): 692-701.

[8] 刘旭亮, 黄玉平，崔佩娟，等. 柔性机械手建模及动力学特性分析[J]. 噪声与振动控制, 2014,34(6): 7-11.

LIU Xuliang, HUANG Yuping, CUI Peijuan, et al. Modeling and Dynamic Characteristic Analysis of Flexible Robotic Arm[J].Noise and Vibration Control, 2014,34(6): 7-11.