基于时变零相位滤波的变转速滚动轴承故障诊断
2018-02-05陈向民晋风华李录平
陈向民 张 亢 晋风华 李录平
长沙理工大学能源与动力工程学院,长沙,410076
0 引言
滚动轴承是旋转机械设备中最为常用的零部件之一,其工作状态正常与否直接影响到整台设备的性能。当滚动轴承出现点蚀、裂纹等局部故障时,故障元件的固有频率会被故障元件的通过频率所调制[1]。有效解调出滚动轴承故障信号中的调制频率是准确诊断滚动轴承故障的关键。
变转速下机械设备的振动信号中往往包含了丰富的状态信息,一些在平稳运行时不易体现的故障特征可能会被充分表现出来[2-3]。当滚动轴承处于变转速下运行时,其调制信号中的调制频率与转速相关,也为一时变量,直接对解调信号进行频谱分析会产生“频率混叠”现象[4]。
阶次跟踪是工程上常用的一种变转速工况下的信号分析方法。它根据参考轴的转速对信号进行等角度重采样,能提取振动信号中与转速有关的信息[5-6]。但由于机械设备中的零部件众多,其振动信号中与转速相关的调制信号成分也较多,且各种调制信号成分之间的能量强弱不同,特别对微弱故障而言,其故障特征容易被其他特征所淹没,因此,需预先对调制信号中的各调制成分进行分离。
常用的自适应信号分离方法主要有EMD(empirical mode decomposition)[7-8]、EEMD(ensemble empirical mode decomposition)[9-10]、LMD(local mean decomposition)[11-12],VMD(variational mode decomposition)[13]等方法,这些方法在滚动轴承故障特征提取中均取得了一定的效果。但当两调制信号的频率比较接近时,却无法有效分离。对于多调制信号的分离问题,文献[14]提出了基于线调频小波路径追踪(chirplet path pursuit,CPP)的自适应时变滤波方法,但该方法滤取的信号存在时延。为此,文献[15]提出采用零相位滤波,有效解决了时延问题,并将其应用于载波频率(即齿轮啮合频率)和调制频率(即轴转频)的分析中。但对于滚动轴承来说,其载波频率(即共振频率)为一定值,因此,不能直接使用该方法对变转速下的滚动轴承故障振动信号进行分析,且当载波频率被多个调制频率同时调制时也无法有效分离。
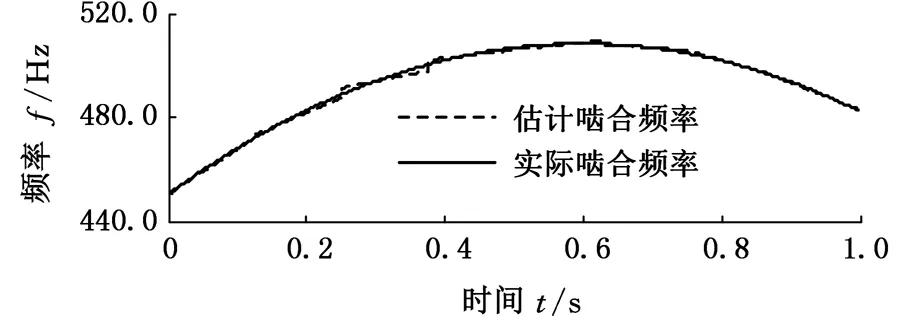
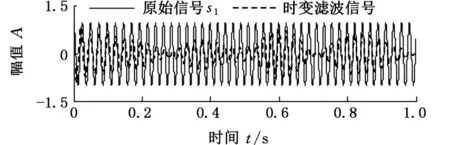
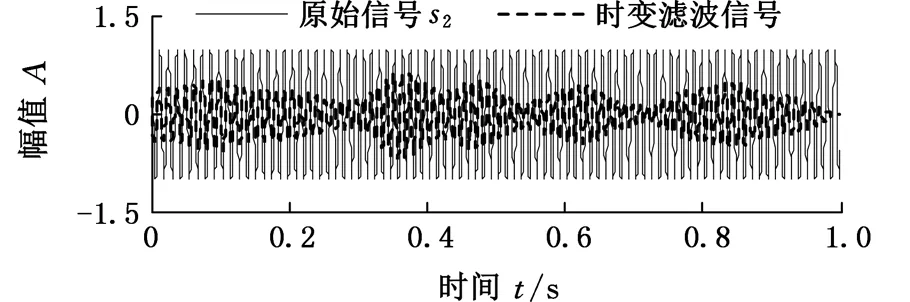
综上所述,针对变转速下滚动轴承故障特征的提取与分离,本文将CPP算法[16-18]与零相位滤波相结合,并将其用于变转速下的滚动轴承故障特征的提取与分离。对变转速下的滚动轴承故障振动信号进行算法仿真和应用实例分析,结果表明,本文方法可在强噪声环境下有效分离变转速滚动轴承的故障调制特征。
1 线调频小波路径追踪算法
线调频小波路径追踪(CPP)算法采用的多尺度线调频基元函数库为
D(haμbμI)={haμbμI(t)}=
{KaμbμIe[-i(aμt+bμt2)]LI(t)}
(1)
其中,D表示基元函数库;haμbμI(t)为多尺度线调频基元函数;I表示动态分析时间段,I=[kN2-j,(k+1)N2-j];N为分析信号长度;k为动态时间段的序号,k=0,1,…,2j-1;j为分析尺度系数,j=0,1,…,lb(N-1);KaμbμI为归一化系数,满足‖haμbμI‖=1;aμ和bμ分别为频率偏置系数和调频率,且满足aμ+2bμt 采用多尺度线性调频基元函数对分析信号进行逐段投影,并计算每个时间分析段I内的投影系数和对应的线调频基元函数。分析信号与多尺度线性调频基元函数的相似性越高,其投影系数也就越大,此时,基元函数对应的能量也就越大。因此,需寻求一种动态连接算法Π,使得所连接基元函数对应的信号在整个分析时间内的总能量最大,且连接算法Π应覆盖整个分析时间段,不重叠,即 (2) 式中,1I(t)为矩形滤波器,数字1表示矩形滤波器的幅值为常量1。 此时,对应的投影系数集合和基元函数集合分别为 (3) CPP方法中连接算法Π的连接步骤如下: (1)初始化。以i表示分析时间段序号,di表示第i个时间段之前的分解信号,ei表示第i个时间段的分解信号,Edi表示第i个分析时间段之前分解信号的总能量,li表示连接到第i个分析时间段的前一分析时间段序号,Eei表示第i个分析时间段投影系数对应的分解信号的能量。初始化时,Edi=0,li=0。 (2)对于动态分析时间段集合I={I1,I2…}中的每一个元素Ii,查找出与其相邻的所有下一个动态分析时间段集合{Ij},如果 Edi+Eei>Edj (4) 则有 (5) 连接算法Π可保证在整个分析时间段内基元函数组合所对应的信号与分析信号最为相似。基元函数在动态分析时间支持区Ii内的瞬时频率fIi(t)=aμ+2bμt,ti∈Ii,将所有动态时间段集合I={I1,I2…}中所对应的频率曲线集合fI={fI1,fI2…}按时间先后顺序连接成线则为信号在整个分析时间段内的瞬时频率估计。 零相位滤波是一种滤波思想,不涉及具体的滤波器,可以是FIR滤波器,也可以是IIR滤波器。零相位滤波中的FRR(forward-reverse filtering, reverse output)法是先将输入信号x(t)按顺序进行滤波,然后将所得结果逆转后反向通过滤波器,再将结果逆转后输出,便可得到滤波信号y(t)[19],其频域表达式为 (6) 式中,X(ejω)为输入信号x(t)的频谱;Y(ejω)为输出信号的频谱;H(ejω)为滤波器的幅频特性。 由式(6)可得 Y(ejω)=X(ejω)|H(ejω)|2 (7) 由式(7)可看出,输出信号与输入信号之间仅在幅值上相差|H(ejω)|2,相位上并无时延或畸变,即实现了零相位滤波。 时变零相位滤波器可由经典零相位滤波方法设计而来,即根据信号的频率变化,在每一时刻均设计一个零相位滤波器[14],即 H(ejω,ti)=Hi(ejω)i=1,2,…,N (8) 假定分析信号为x(ti),i=1,2,…,N,CPP算法估计出的频率为f(ti),调制信号的阶次为O,则时变零相位滤波器的设计步骤如下: (9) (10) 时变零相位滤波方法可根据信号的频率变化特点自适应地进行滤波,因而非常适合频率变化下的信号分析。 当齿轮箱中的滚动轴承出现点蚀、裂纹等局部故障时,故障元件的固有频率会被故障元件的通过频率所调制。滚动轴承内外圈局部故障的故障特征频率计算公式分别如下[1]: (11) (12) 式中,Z为滚动体个数;fr为轴的转频;d0为滚动体直径;D为节径;α为接触角。 齿轮箱的转速发生改变,轴承的故障特征频率也会随之发生改变,此时,基于平稳分析的包络谱分析不能很好地表征轴承的故障特征。但对于同一轴承,无论转速如何变化,其故障特征阶次却是一定值(即只与轴承本身的参数相关)。内外圈的故障特征阶次计算公式分别为 (13) (14) 因此,本文针对变转速下滚动轴承故障调制信息的提取与分离,将CPP算法和零相位滤波器设计相结合,提出了基于时变零相位滤波的变转速滚动轴承故障诊断方法。该方法先采用CPP算法从故障轴承信号中估计齿轮箱中的啮合频率,并根据啮合频率与齿轮齿数求取转速,同时,采用Hilbert包络解调方法求取轴承故障信号的包络信号;然后根据转速信号分别设计各故障特征阶次处的时变零相位滤波器,再采用各时变零相位滤波器对包络信号进行分析,便可得到各阶调制信号;最后根据转速信号对各阶调制信号进行阶次分析,并根据阶次谱诊断轴承故障。本文算法流程如图1所示。 图1 算法流程框图Fig.1 Algorithm flow chart 为验证本文方法分离轴承故障调制特征的有效性,设置仿真合成信号s为 s=sbe+sge+sno (15) (16) sge=1.8[1+0.5cos(6πt3+10.8t2+50πt)]· (17) 其中,sbe为轴承故障信号,轴承的固有频率为1400 Hz,其三阶故障特征阶次分别为1.6、3.2和4.8,轴承故障信号分量如图2a所示;sge为齿轮信号分量,其中信号的幅值为1.8,模拟齿数为18,啮合频率被1倍转频调制,调制信号幅值为0.5,齿轮信号分量如图2b所示;sno为强度为-6 dB的高斯白噪声。合成信号s的时域波形如图2c所示。 (a)轴承故障信号分量 (b)齿轮信号分量 (c)合成信号图2 仿真信号分量及合成信号Fig.2 Simulation signal components and its composite signal 采用Hilbert解调分析求取合成信号的包络,得到的包络信号如图3所示。 图3 仿真合成信号的包络信号Fig.3 Envelope signal of the composite signal 设置频率偏置系数的搜寻范围为430~530 Hz,搜寻分辨率为1 Hz;调频率的搜寻范围为-200~200 Hz/s,搜寻分辨率为1 Hz/s(需要说明的是,对于频率偏置系数和调频率的取值,可采用短时傅里叶变换等时频分析方法大致估计信号的频率变化范围,再适当将变化范围扩大作为取值范围,其取值范围的大小只影响计算时间,对计算结果无影响)。根据上述参数采用CPP方法对合成信号进行分析,估计出的齿轮啮合频率如图4中的虚线所示。图4所示的实线为实际的啮合频率。 图4 估计的啮合频率和实际啮合频率对比Fig.4 Comparison of estimated meshing frequency and actual meshing frequency 根据图4中估计的啮合频率设计前3阶故障特征阶次处的时变零相位滤波器,得到的3个时变零相位滤波器的时频特性如图5所示,图中浅色区域为时变零相位滤波器的通带。图5a~图5c分别对应轴承3个调制频率处时变滤波器的时频特性。 (a)一阶时变零相位滤波器 (b)二阶时变零相位滤波器 (c)三阶时变零相位滤波器图5 各时变零相位滤波器的时频特性Fig.5 Time-frequency characteristic of each time-varying zero-phase filter 根据图5中的3个时变零相位滤波器分别对图3所示包络信号进行时频滤波,得到的3个信号分量分别如图6~图8所示,其中,实线为原始信号,虚线为时变滤波获取的信号。图7b和图8b分别为图7a和图8a在时间段0.1~0.3 s的局部放大图。对比图6、图7b、图8b中的实线和虚线可知,时变滤波信号与原始信号仅在幅值上存在一定的差异,而相位上无畸变。 图6 一阶滤波信号Fig.6 The first order filtered signal (a)二阶滤波信号 (b)二阶滤波信号局部放大图图7 二阶滤波信号及其局部放大图Fig.7 The second order filtered signal and itspartial enlargement (a)三阶滤波信号 (b)三阶滤波信号局部放大图图8 三阶滤波信号及其局部放大图Fig.8 The third order filtered signal and its partial enlargement 对提取的三个滤波信号分别进行阶次谱分析,结果如图9所示。图9a~图9c中,分别在阶次1.591、3.218、4.809处出现了显著峰值,与信号设置的阶次1.6、3.2、4.8相符,验证了本文方法提取和分离轴承故障调制特征的有效性。 (a)一阶滤波信号的阶次谱 (b)二阶滤波信号的阶次谱 (c)三阶滤波信号的阶次谱图9 滤波信号的阶次谱Fig.9 Order spectrums of the filtered signals 为增加对比,采用图4中的估计啮合频率直接对图3中的包络信号进行阶次分析,得到的阶次谱如图10所示。图10中,在轴承故障阶次1.591和3.218处出现了峰值,但在三阶轴承故障阶次4.8处未出现峰值,且在转频阶次0.998处出现了明显峰值。 图10 仿真合成信号的包络阶次谱Fig.10 Envelope order spectrum of the simulation composite signal 同时,采用EEMD方法对图3所示包络信号进行分解,并对分解后的IMF进行阶次分析,以获取各IMF的阶次谱。图11a、图11b分别为第4和第5个IMF的阶次谱,图中,在轴承故障阶次1.591、3.181、4.809处分别出现了峰值,但在非轴承故障调制阶次3.921处出现了未知峰值。 (a)IMF4的阶次谱 (b)IMF5的阶次谱图11 IMF4与IMF5的阶次谱Fig.11 Order spectrum of IMF4 and IMF5 为验证本文方法在实测变转速轴承故障振动信号中分离轴承故障调制特征的有效性,在齿轮箱上进行变转速轴承故障试验。试验齿轮箱主动齿与从动齿的齿数均为37。试验轴承为6307E型滚动轴承,轴承参数如表1所示。将表1中参数代入式(13)、式(14)计算可得,轴承外圈局部故障和内圈局部故障的一阶故障调制特征阶次分别为3.06和4.93。 表1 滚动轴承参数 为模拟轴承故障,利用激光分别在轴承外圈和内圈上切割宽为0.15 mm、深为0.13 mm的槽,以模拟外圈和内圈局部故障。轴承故障样本如图12所示。 (a)轴承外圈故障 (b)轴承内圈故障图12 轴承故障样本Fig.12 Faulted bearings sample 试验采用调速电机使轴承在变转速下运行。试验时,采用LMS采集仪同步采集振动加速度信号和转速信号,以便进行对比分析。 对外圈故障滚动轴承进行试验,采样频率为8192 Hz,采样时长为2 s。轴承外圈故障振动信号的时域波形如图13所示。图14 为图13的包络信号。 图13 变转速轴承外圈故障振动信号Fig.13 Vibration signal of bearing with outer-race failure under variable rotational speed 图14 变转速轴承外圈故障的包络信号Fig.14 Envelope signal of bearing with outer-race failure under variable rotational speed 采用CPP方法对轴承外圈故障信号进行分析,估计齿轮的啮合频率如图15中的虚线所示。图15中的实线为实测的啮合频率。 图15 估计的啮合频率与实测啮合频率对比Fig.15 Comparison of estimated meshing frequency and actual meshing frequency 采用本文方法对变转速轴承外圈故障振动信号进行分析,得到的阶次谱如图16所示,图16a~图16c中,分别在阶次3.086,6.171,9.257处出现了显著的峰值,与轴承外圈故障的1~3阶故障阶次吻合,表明轴承外圈出现了局部故障。 根据图15中估计的啮合频率信息对图14所示包络信号直接进行阶次分析,得到包络信号的阶次谱如图17所示。图17中出现了较多的峰值,但这些峰值均与轴承外圈故障的故障阶次有一定差异。 (a)一阶滤波信号的阶次谱 (b)二阶滤波信号的阶次谱 (c)三阶滤波信号的阶次谱图16 轴承外圈故障振动信号的时变滤波分析结果Fig.16 Analysis result of the time-varying filtered vibration signal of bearing with outer-race failure 图17 变转速轴承外圈故障包络信号的阶次谱Fig.17 Order spectrum of envelope signal of bearing with outer-race failure under variable rotational speed 采用EEMD方法对图14所示包络信号进行分解,并根据图15中估计的啮合频率曲线对分解后的IMF进行阶次分析,得到的阶次谱如图18所示。图18a~图18c分别为IMF6~IMF8的阶次谱,在阶次3.086、6.171、9.171处出现峰值,与轴承外圈故障特征阶次基本相符。但在转频阶次1.029、1.971处也出现峰值,且二阶和三阶轴承故障特征阶次6.171、9.171同处于分量IMF6中,未能有效分离。 对内圈局部故障滚动轴承进行试验。采样频率为20480 Hz,采样时长为0.8 s。图19为轴承内圈故障振动信号的时域波形图。 (a)IMF6的阶次谱 (b)IMF7的阶次谱 (c)IMF8的阶次谱图18 变转速轴承外圈故障IMF6~IMF8的阶次谱Fig.18 Order spectrum of IMF6~IMF8 of bearing with outer-race failure under variable rotational speed 图19 变转速轴承内圈故障振动信号Fig.19 Vibration signal of bearing withinner-racefailure under variable rotational speed (a)一阶滤波信号的阶次谱 (b)二阶滤波信号的阶次谱图20 轴承内圈故障振动信号的时变滤波分析结果Fig.20 Analysis result of the time-varying filtered vibration signal of bearing with inner-race failure 采用本文的时变滤波方法对图19信号进行分析,分析结果如图20所示。图中,在阶次4.982和阶次9.817处存在显著峰值,与轴承内圈局部故障的一阶和二阶特征阶次相符,故可判断轴承内圈出现了局部故障。 同时,直接采用包络阶次分析方法对图19所示信号进行分析,得到的阶次谱如图21所示。图21中,在阶次4.982处存在峰值,与轴承内圈局部故障的一阶特征阶次相符,但二阶特征阶次处无显著峰值,且阶次谱中存在众多的干扰阶次。 图21 变转速轴承内圈故障包络信号的阶次谱Fig.21 Order spectrum of envelope signal of bearing with outer-race failure under variable rotational speed 采用基于EEMD的包络阶次分析方法对图19所示信号进行分析,分析结果如图22所示。图22中,在阶次9.894和4.947处存在峰值,与轴承内圈故障的一、二阶特征阶次相符。但与图20相比,图22中存在较多的噪声干扰,分析效果要逊色于图20分析结果。 (a)IMF6的阶次谱 (b)IMF7的阶次谱图22 变转速轴承内圈故障IMF6~IMF7的阶次谱Fig.22 Order spectrum of IMF6~IMF7 of bearing with outer-race failure under variable rotational speed (1)时变零相位滤波器根据调制信号的频率变化特点,能自适应地滤取调制信号,无相位畸变,且具有较强的抗噪能力。 (2)与EEMD等方法进行了对比研究,结果表明,时变零相位滤波方法不仅能有效提取轴承故障调制特征,而且可实现其各调制特征的有效分离。 (3)由于滤波器在通带内的幅频特性会有一定的波动,因此,滤取的调制信号的幅值较原始信号会有一定的幅值畸变,如何减少滤波后信号幅值的畸变可进一步研究。 [1] 丁康,李巍华,朱小勇. 齿轮及齿轮箱故障诊断实用技术[M]. 北京:机械工业出版社,2005. DING Kang,LI Weihua,ZHU Xiaoyong. The Gear and Gearbox Fault Diagnosis Practical Technology[M]. Beijing:China Machine Press,2005. [2] 李志农,丁启全,吴昭同,等. 旋转机械升降速过程中的双谱-FHMM识别方法[J]. 振动工程学报,2003,16(2): 171-174. LI Zhinong, DING Qiquan, WU Zhaotong, et al. Study on Bispectrum-FHMM Recognition Method in Speed-up and Speed-down Process of Rotating Machinery[J]. Journal of Vibration Engineering, 2003,16(2):171-174. [3] 张亢,程军圣. 基于LMD和阶次跟踪分析的滚动轴承故障诊断[J]. 振动、测试与诊断,2016,36(3):586-591. ZHANG Kang, CHENG Junsheng. A Fault Diagnosis Method for Rolling Bearing Based on LMD and Order Tracking Analysis[J]. Journal of Vibration, Measurement & Diagnosis,2016, 36(3): 586-591. [4] 康海英,栾军英,郑海起,等. 基于阶次跟踪和经验模态分解的滚动轴承包络解调分析[J]. 机械工程学报,2007,43(8):119-122. KANG Haiying, LUAN Junying, ZHENG Haiqi, et al. Envelope Demodulation Analysis of Bearing Based on Order Tracking and Empirical Mode Decomposition[J]. Chinese Journal of Mechanical Engineering, 2007, 43(8): 119-122. [5] 郭瑜,秦树人,汤宝平,等. 基于瞬时频率估计的旋转机械阶比跟踪[J]. 机械工程学报,2003,39(3): 32-36. GUO Yu, QIN Shuren, TANG Baoping, et al. Order Tracking of Rotating Machinery Based on Instantaneous Frequency Estimation[J]. Chinese Journal of Mechanical Engineering, 2003, 39(3): 32-36. [6] BORGHESANI P,PENNACCHI P,RANDALL R B,et al. Order Tracking for Discrete-random Separation in Variable Speed Conditions[J].Mechanical Systems and Signal Processing,2012,30:1-22. [7] 孟宗,闫晓丽,王赛. 基于HMM校正与神经网络延拓的EMD端点效应抑制方法[J]. 中国机械工程,2015,26(14): 1920-1925. MENG Zong, YAN Xiaoli, WANG Sai. Restraining Method of End Effect for EMD Based on Error Calibration by HMM and Neural Network[J]. China Mechanical Engineering, 2015, 26(14): 1920-1925. [8] CHENG Junsheng, YU Dejie, YANG Yu. A Fault Diagnosis Approach for Roller Bearings Based on EMD Method and AR Model[J]. Mechanical System and Signal Processing, 2006, 20: 350-362. [9] 何青,褚东亮,毛新华. 基于EEMD和MFFOA-SVM的滚动轴承故障诊断[J]. 中国机械工程,2016,27(9): 1191-1197. HE Qing, CHU Dongliang, MAO Xinhua. Study on Rolling Bearing Fault Diagnosis Based on EEMD and MFFOA-SVM[J]. China Mechanical Engineering, 2016, 27(9): 1191-1197. [10] LEI Yaguo, HE Zhengjia, ZI Yanyang. Application of the EEMD Method to Rotor Fault Diagnosis of Rotating Machinery[J].Mechanical System and Signal Processing, 2009, 23(4): 1327-1338. [11] 孟宗,闫晓丽,王亚超. 基于LMD和HMM的旋转机械故障诊断[J]. 中国机械工程,2014,25(21): 2942-2946. MENG Zong, YAN Xiaoli, WANG Yachao. Rotating Machinery Fault Diagnosis Based on Local Mean Decomposition and Hidden Markov Model[J]. China Mechanical Engineering, 2014, 25(21): 2942-2946. [12] CHENG Junsheng, ZHANG Kang, YANG Yu. An Order Tracking Technique for the Gear Fault Diagnosis Using Local Mean Decomposition Method[J]. Mechanism and Machine Theory,2012,55: 67-76. [13] 唐贵基,王晓龙. 变分模态分解方法及其在滚动轴承早期故障诊断中的应用[J]. 振动工程学报,2016,29(4): 638-648. TANG Guiji, WANG Xiaolong. Variational Mode Decomposition Method and Its Application on Incipient Fault Diagnosis of Rolling Bearing[J]. Journal of Vibration Engineering, 2016, 29(4): 638-648. [14] 彭富强,于德介,吴春燕. 基于自适应时变滤波阶比跟踪的齿轮箱故障诊断[J]. 机械工程学报,2012,48(7): 77-85. PENG Fuqiang, YU Dejie, WU Chunyan. Self-adaptively Time-varying Filter Based Order Tracking Method and Its Application in Gearbox Fault Diagnosis[J]. Chinese Journal of Mechanical Engineering, 2012, 48(7): 77-85. [15] WU Chunyan, LIU Jian, PENG Fuqiang, et al. Gearbox Fault Diagnosis Using Adaptive Zero Phase Time-varying Filter Based on Multi-scale Chirplet Sparse Signal Decomposition[J]. Chinese Journal of Mechanical Engineering, 2013, 26(4): 831-838. [17] LUO Jiesi, YU Dejie, LIANG Ming. Gear Fault Detection Under Time-varying Rotating Speed via Joint Application of Multiscale Chirplet Path Pursuit and Multiscale Morphology Analysis[J]. Structural Health Monitoring, 2012, 11(5):526-537. [18] 陈向民, 于德介, 任凌志,等. 基于线调频小波路径追踪阶比能量解调的齿轮轮齿裂纹故障诊断[J]. 中国机械工程, 2011, 22(21): 2598-2603. CHEN Xiangmin, YU Dejie, REN Lingzhi, et al. Order Energy Demodulating Approach Based on Chirplet Path Pursuit and Its Application to Gear Tooth Crack Fault Diagnosis[J]. Journal of Vibration Engineering, 2011, 22(21): 2598-2603. [19] 纪跃波,秦树人,汤宝平. 零相位数字滤波的方法与实现[J]. 振动、测试与诊断,2000,20(增刊): 167-172. JI Yuebo, QIN Shuren, TANG Baoping.Method and Realization of Zero Phase Digital Filter[J]. Journal of Vibration, Measurement & Diagnosis, 2000, 20(S): 167-172.2 时变零相位滤波器
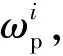
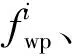
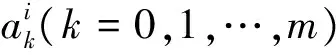
3 变转速下的滚动轴承故障诊断原理
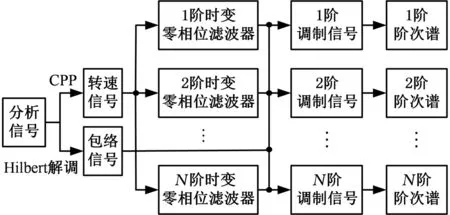
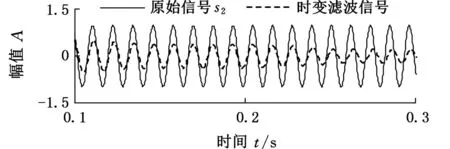
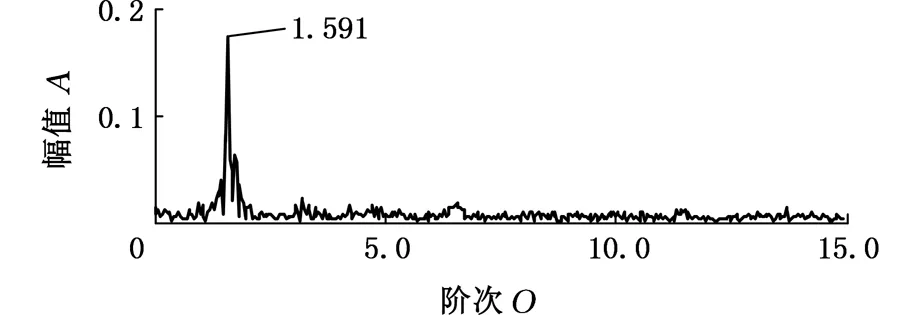
4 算法仿真
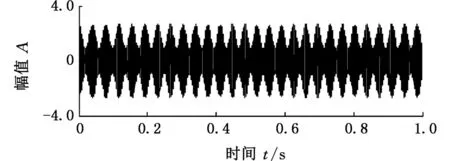
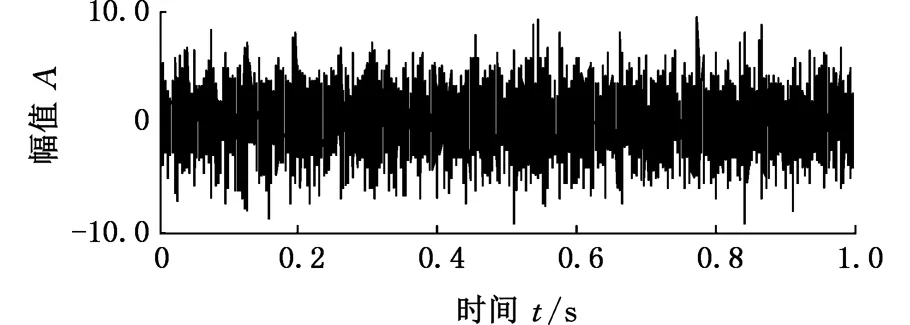
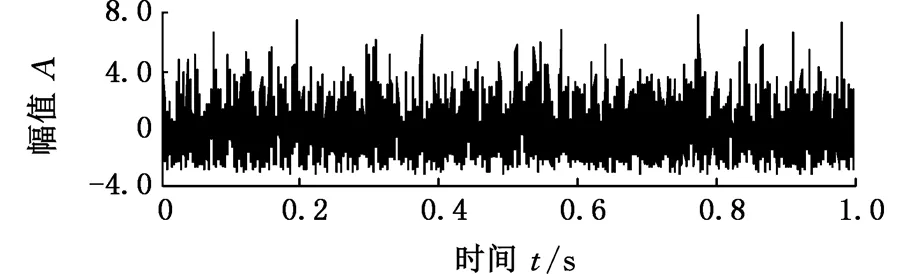
cos(108πt3+194.4πt2+900πt)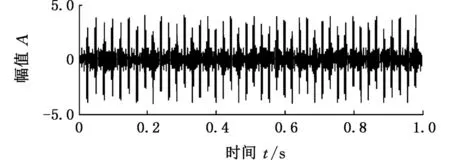


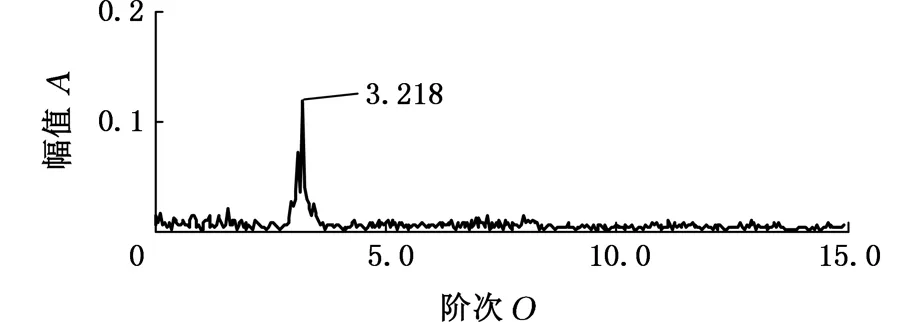
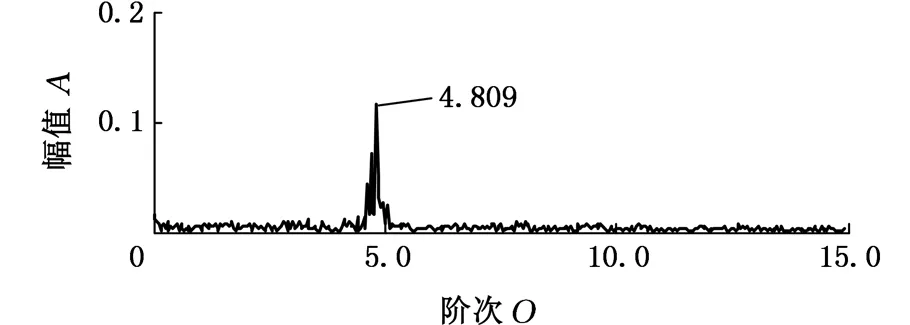

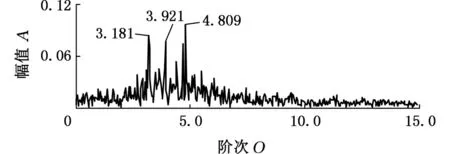
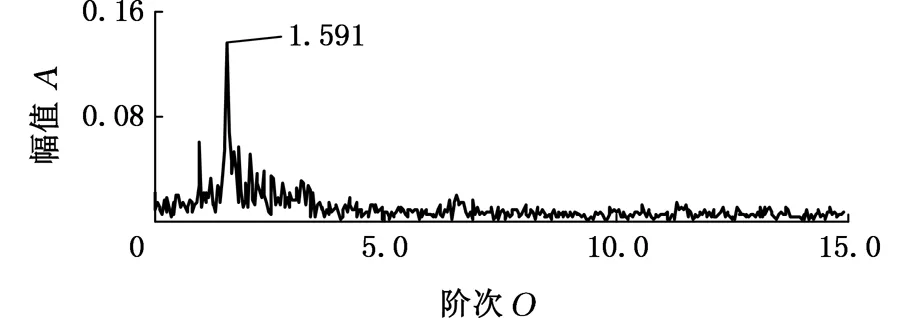
5 应用实例


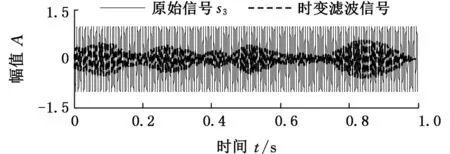
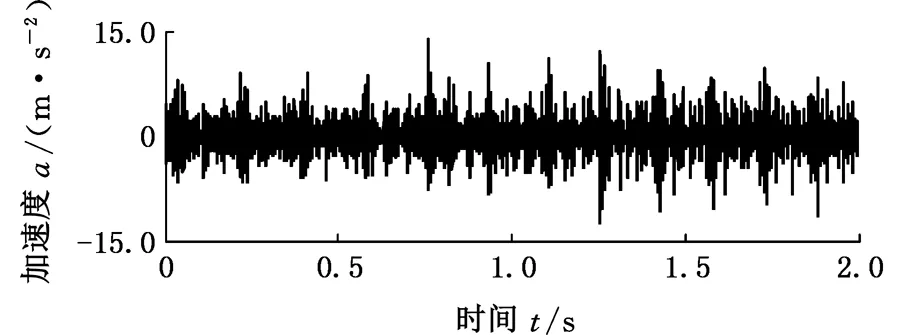
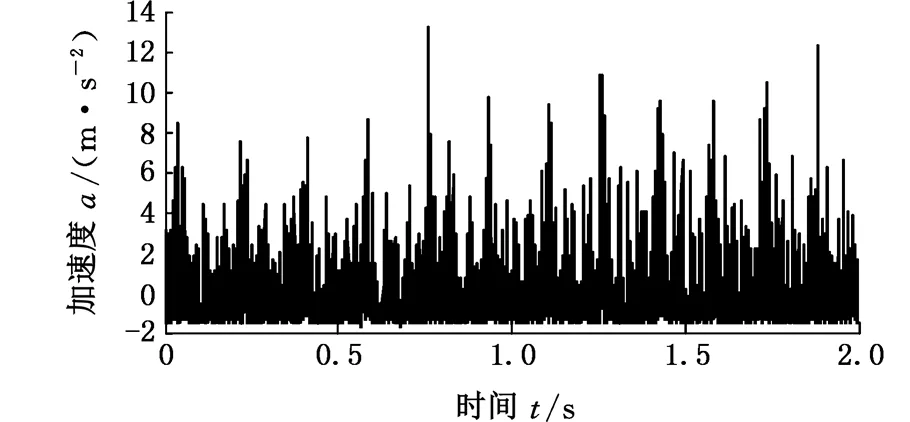
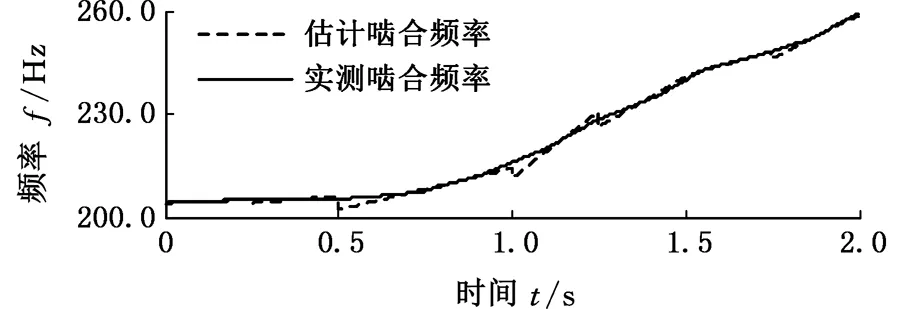
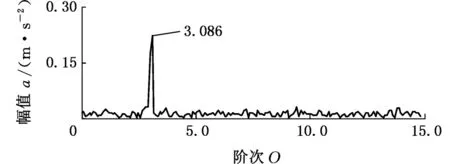
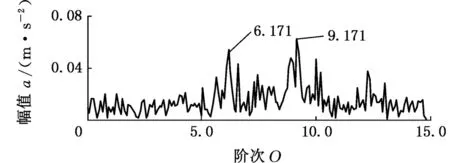
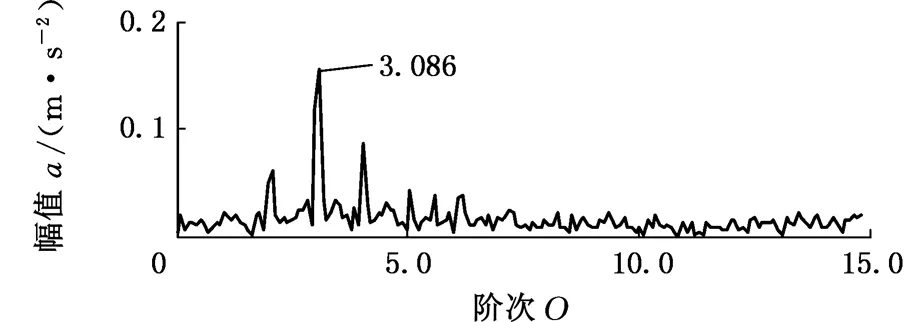
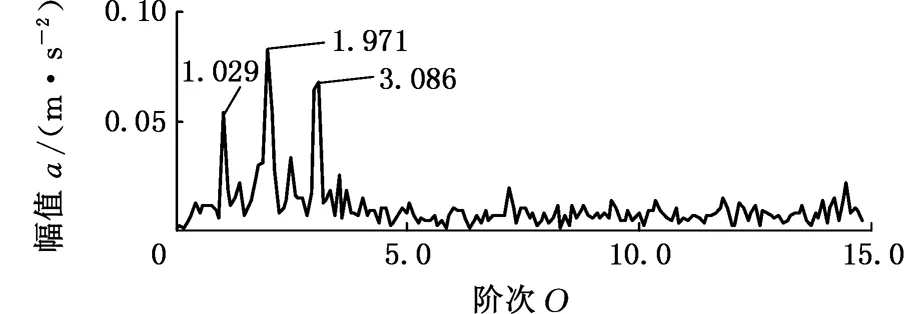
5.1 变转速轴承外圈局部故障振动信号分析
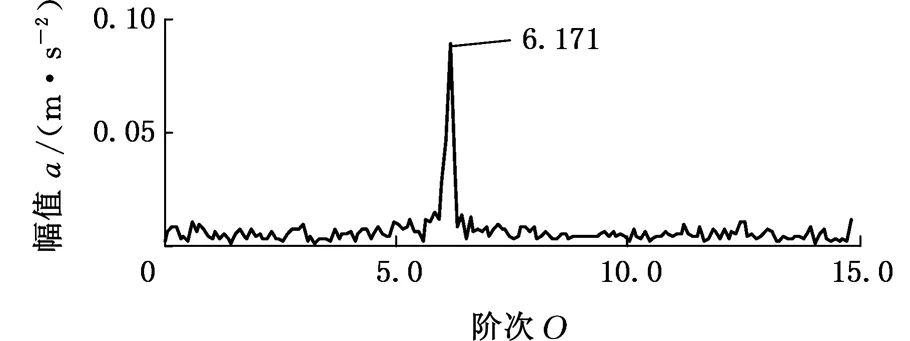
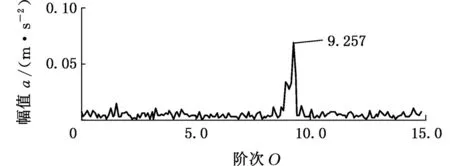
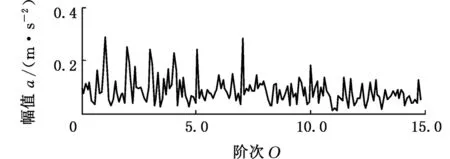
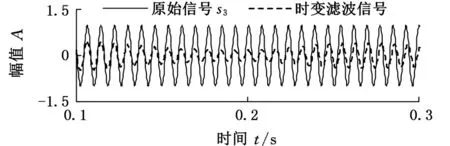
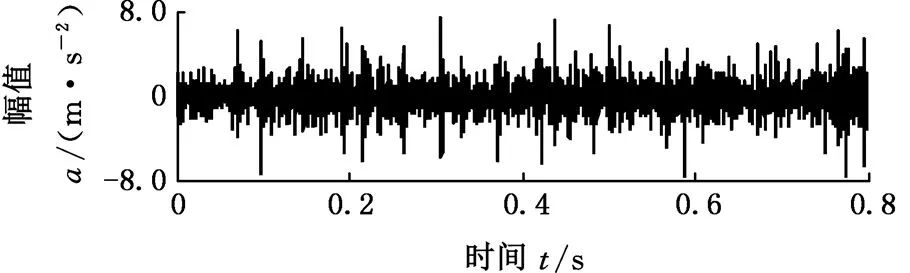
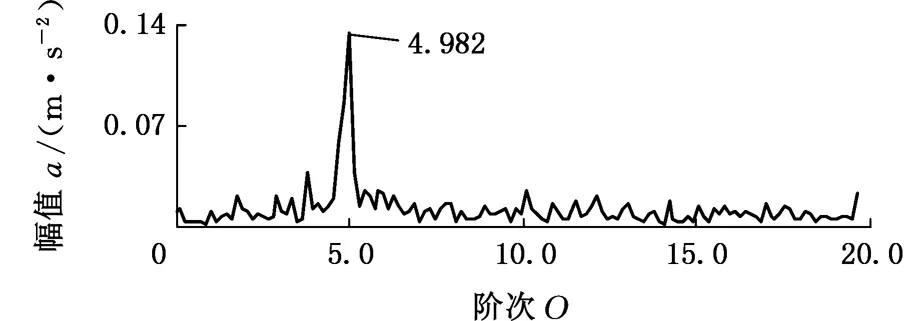
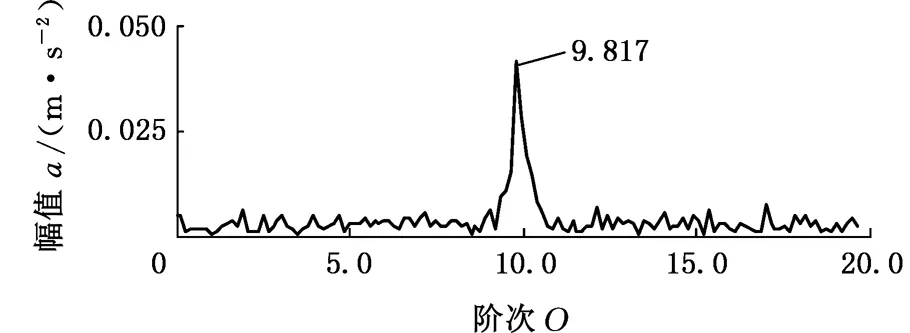
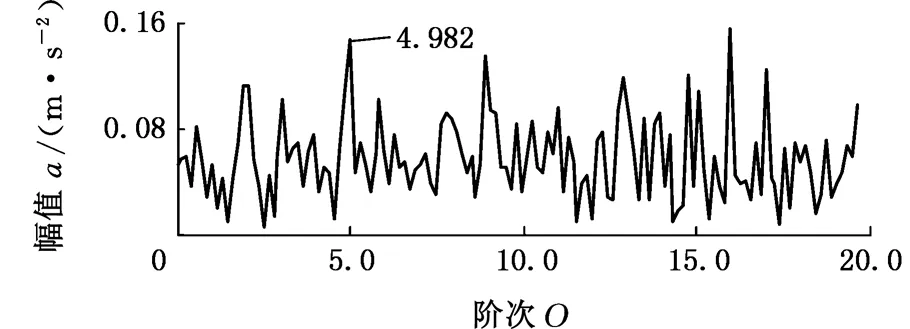
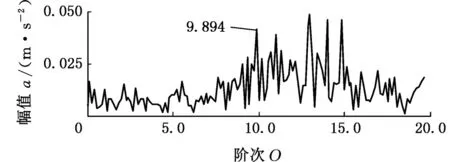
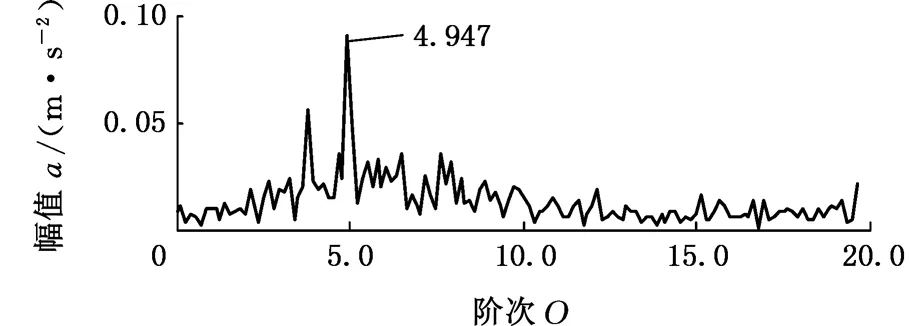
5.2 变转速轴承内圈局部故障振动信号分析
6 结论
