高速列车的样本关联改进故障诊断方法
2018-02-05罗怡澜邹益胜宋小欣
张 楷 罗怡澜 邹益胜 王 超 宋小欣
西南交通大学机械工程学院,成都,640031
0 引言
通过故障诊断可对高速列车进行实时故障监控,在检修维护前进行故障定位,为零部件周期更换提供依据。高速列车系统振动信号受车体和转向架耦合关系、轨道随机激励等多种因素共同影响,属于典型的非平稳信号,通过振动信号进行故障诊断是一种行之有效的方法[1]。
加拿大Ultra-Tech公司开发的组合式转向架监控系统可对转向架蛇形失稳故障及机车轴箱发热等故障进行监测与预报;法国Banbadi公司对机车车辆转向架蛇行失稳开展了持续研究;英国AME公司在客车上安装温度传感器和振动传感器,进行状态监测;瑞典SKF公司对铁路机车车辆新型轴承开展了研发和制造,并对机车轴承的运行状态开展监测诊断[2]。国内的高速列车故障诊断研究中,丁夏完等[3]釆用自适应短时傅里叶变换对货车滚动轴承振动信号进行时频分析和故障信息提取。陈特放等[4]釆用小波变换研究了由损伤冲击造成的机车车辆走行部振动信号突变的时频特征;马莉等[5]釆用小波变换对列车运行中踏面与轨道产生的振动检测数据处理算法进行了研究;秦娜等[6]通过SIMPACK动力学仿真提取高速列车转向架信号特征,提出信息测度理论框架,研究了多特征融合与降维。然而,采用小波包特征提取和支持向量机(support vector machine,SVM)模式识别结合的方法进行故障诊断,存在基函数、分解层数和SVM核函数等经验性选择问题,同时,SVM具有局部极小点、收敛慢、网络学习和记忆不稳定等缺陷。
聚合经验模态分解(ensemble empirical mode decomposition,EEMD)是一种针对非平稳信号的自适应非线性信号处理方法,能将非平稳信号按时间尺度进行分解[7],从而得到高频到低频分布的本征模态函数(intrinsic mode function,IMF)分量,避免了参数经验性选择问题。基于变量预测模型的模式识别(variable predictive model based class discriminate,VPMCD),根据故障信号特征值之间的内在关系建立数学模型,通过回归分析确定模型参数,避免了神经网络中结构类型、SVM核函数及其参数的选择等经验性问题和迭代寻优过程,具有算法运算量小和识别结果稳定的优势[8-9]。杨宇等[10-12]通过主成分估计法进行预测模型参数估计并结合人工鱼群智能算法实现VPMCD的改进;潘海洋等[13-14]通过引入LE流形学习算法进行特征压缩并采用Kriging模型代替原模型的方法对VPMCD算法进行了改进。
上述方法对滚动轴承故障诊断识别效果较好,在样本足够的情况下,对高速列车故障诊断也取得了较好的识别效果。然而在高速列车故障诊断的研究中发现还存在以下问题需要解决:①小样本不适用。高速列车机械系统故障诊断所提取的特征量较多,用于参数回归的样本需求量也相应增加,当样本量不足时,原方法不适用。②随机突变点造成识别率降低。高速列车工况多变,轨道不平顺、弯道,列车间和部件间相互作用等随机激励因素造成样本突变点,降低了高速列车故障诊断识别率。
针对上述问题,本文基于EEMD故障特征分解和VPMCD模式识别方法,通过EEMD分解提取故障特征矩阵,进一步通过滑窗逐步回归估计VPMCD预测模型的参数;同时,利用相邻故障样本间的相关性和连续性,对突变样本进行平滑性处理,减小了突变样本对识别结果的影响,从而有效提高了高速列车复杂机械系统的故障识别率和稳定性。
1 EEMD及特征提取
1.1 EEMD原理
EEMD是经验模态分解(EMD)的改进方法,EMD方法主要通过三次样条对信号极值点进行包络,获取该信号的IMF分量,但如果信号极值点分布不均匀,则提取的IMF分量会出现模态混叠的情况。
为此,WU等[7]将白噪声加入待分解信号,把信号和噪声的组合看成一个总体,利用白噪声频谱的均布特性抑制模态混叠,经过多次平均运算处理后,噪声将相互抵消,集成均值的结果就可直接作为最终结果,EEMD的原理如图1所示。
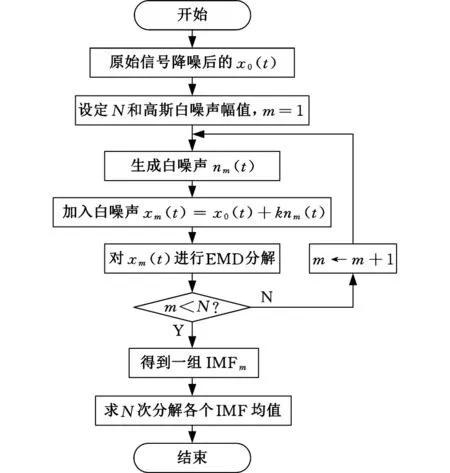
图1 EEMD分解原理及流程Fig.1 EEMD decomposition principle and flow chart
1.2 故障特征提取
原信号经过EEMD获取各IMF分量,采用相关系数法求出各IMF与原信号的相关系数,如表1所示。根据表1选取了与原信号相关系数大于0.004的IMF分量(IMF1~IMF6),进行特征提取。
考虑到高速列车故障种类众多,不同时频域特征对不同故障类型的识别效果各有侧重,根据振动信号的机械故障特征提取[1]、信息测度特征提取[6]和高速列车熵特征提取[15]的理论,对原信号和IMF1~IMF6各分量提取时域特征、频域特征和时频域特征,组合使用时得到一个164维特征量组成的特征矩阵,如表2所示。

表2 故障特征提取
2 VPMCD分类器及其改进
2.1 VPMCD原理
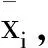
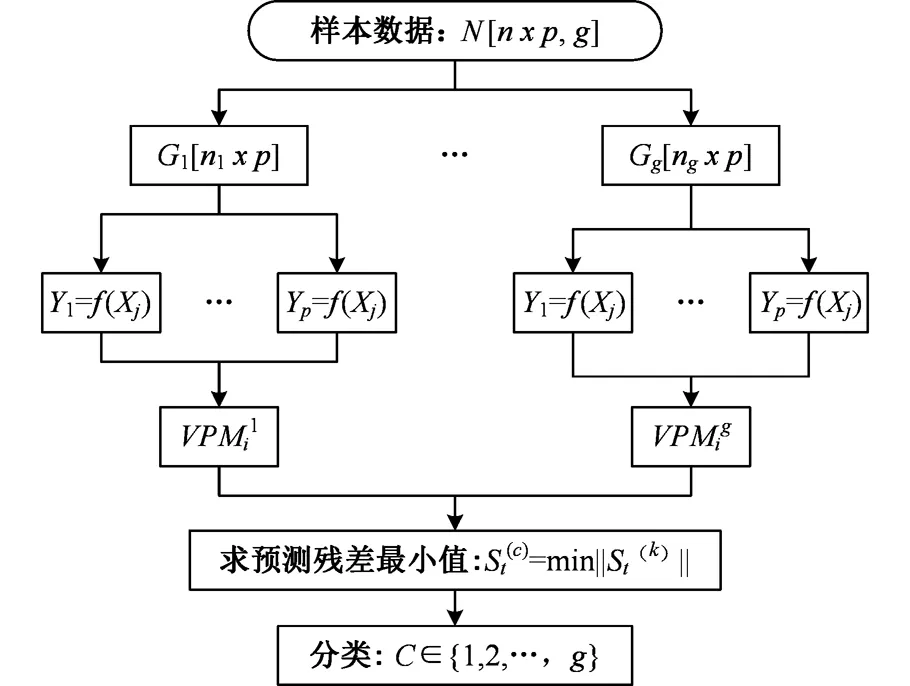
图2 VPMCD模式识别原理Fig.2 VPMCD pattern recognition principle
2.2 基于滑窗逐步回归和样本关联的VPMCD改进
RAGHURAJ等[8]提出的VPMCD方法从本质上来说,是对线性模型(L)、线性交互模型(LI)、二次交互模型(QI)、二次模型(Q)进行参数估计,通过模型的回归分析结果对特征变量进行预测,从而得出实时监测样本的特征量与预测结果的残差平方和,以此作为分类依据。四种预测模型如下。
线性模型(L):
(1)
式中,r为模型阶数,r=1,2,…,p-1。
线性交互模型(LI):
(2)
二次交互模型(QI):
(3)
二次模型(Q):
(4)
对于不同的特征值,其预测模型类型、预测变量、模型阶数有可能不同。
除L模型外,其余3种模型均为非线性模型,因此该问题本质上是多元多重回归问题。根据最小二乘法回归分析,方程个数(样本数)需大于待估计变量个数,可知4种模型需要的最小样本数:
nL=r+1
(5)
nLI=(r2-r)/2+1
(6)
nQI=r(r+1)/2
(7)
nQ=2r-1
(8)
由式(5)~式(8)可知,该方法有最小样本数限制,当特征维数较大时不适用于小样本数据,因此限制了该方法的使用。
逐步回归的思想是将变量逐个引入模型,每引入一个变量便进行一次F检验,并对已经选入的解释变量逐个进行t检验,当已引入的变量由于后引入变量变得不再显著时,将其删除,直到没有显著变量入选回归方程为止[16]。从式(1)~式(4)可以看出,与典型多元多重回归模型不同的是,各特征变量在其他变量的预测过程中是自变量;在自身变量预测的时候是因变量,是变量预测模型结果的一部分,不宜直接删除。
高速列车的运行状态虽然受多种随机激励影响,样本间可能出现突变样本,但理论上,同一列车在短时间内的故障状态不会发生突变,其相邻样本间存在关联性和连续性,本文正是利用这一数据特点,对VPMCD方法进行改进。
本文将滑窗逐步回归分析与样本集训练结合,对故障模式进行识别,其具体算法如下(以L模型为例对方法改进思路进行说明)。
2.2.1模型训练过程
(1)对于g类故障分类问题,共收集N个训练样本,第k类故障的样本数为nk。
(2)对所有训练样本提取特征向量X。
(3)对任意被预测变量xi,从L、LI、QI、Q四种模型中选择一种模型类型(本文以L模型为例说明)。
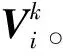
原方法中取r 将第k类故障第j滑窗(滑窗宽度为r)中第e个特征量的L模型计算式用矩阵表示: Xj(k)Be(k)=Yj(k) (9) Xj= (10) Be(k)=[be,1be,2…be,r]T (11) Yj(k)=[x1,e+jx2,e+jxn,e+j]T (12) 式中,e为特征编号,e=1,2,…,r;j为滑窗编号,j=1,2,…,p-r+1,且r+1 (5)通过最小二乘算法求得待估计参数向量Be(k),可得出第k类故障第j滑窗的预测模型Vj(k)即矩阵(本矩阵为对称矩阵,建议取上三角矩阵简化运算): Vj(k)=[B1(k)B2(k) …Br(k)] (13) 2.2.2模型识别过程 (1)对测试样本提取特征向量Xt=(x1,x2,…,xp),其中,t为测试样本号,将其代入式(1),式中参数取Vj(k)的训练结果,可得该测试样本第k类故障第j滑窗的预测向量: (14) 对于L模型,有 (15) (2)求测试样本Xt每个滑窗对应的原特征和第k类预测值的残差之和: (16) 从而求出样本Xt对第k类预测值的残差向量: St(k)=(st,1(k),st,2(k), … ,st,p-r+1(k)) (17) (3)计算第k类故障所有特征的预测残差平方和矩阵。将T个样本作为一个关联样本集输入,分别计算每类故障下各滑窗的预测残差平方和,组成一个式(13)所示的残差平方和矩阵: (18) 该矩阵中的行代表不同样本的计算结果,列代表不同滑窗的计算结果。 (4)根据最小残差平方和确定故障类别。比较各类故障在第t个测试样本第j滑窗下故障特征预测残差平方和,按照下式 st,j(c)=min(st,j(1),st,j(2), …,st,j(g)) (19) 求各故障特征预测残差平方和中的最小值st,j(c),并根据最小值所属类别确定故障类别c。式(19)表达的是,在第j滑窗下,第t个测试样本与第c类故障的训练模型最为匹配,c∈{1,2,…,g}。 (5)以窗宽为r的滑窗遍历测试样本集合T,可得该样本集合的识别矩阵: (20) 最后将矩阵中出现最多的分类作为输出结果。取p=18,r=9,T=10,g=3,得到某识别矩阵计算结果: (21) 式(21)中,行代表某单一样本的识别结果,每行代表一个时间上连续的测试样本,其故障状态不会瞬态突变,因此每一行的输出结果应该是一致的;列代表某矩形窗识别结果。从式(21)可以看出,如果采用单一样本识别,第3行识别的输出结果为1,而实际是第3类故障。根据本文的方法,参考时序相邻样本的识别结果,将CT判别结果中出现次数最多的类作为最终输出类(此为第3类为输出结果),则消除了第3个突变样本的影响,其判别结果更稳定且算法的识别正确率更高。 根据现有的样本数nL、nLI、nQI、nQ,通过式(1)~式(4)反求,每种模型下参数r可取得的最大值。根据实验结果分析,本文方法对识别率高于50%的通道提高较为明显,因此可将识别率高于50%的通道的识别率均值作为约束条件,通过已有数据进行试验设计,根据识别结果确定对样本集容量T的最优取值。 滚动轴承故障诊断数据采用凯斯西储大学轴承数据中心网站公布的数据,通过此套数据验证本文方法针对滚动轴承故障诊断的有效性和优越性。采样频率为12 kHz,电机负载为0.746 kW,转速为1772 r/min,单样本采样点数个数1024,通过EEMD分解获得IMF1~IMF6分量,进行快速傅里叶变换后,求其频域特征重心频率、均方频率、频率方差,组成18维特征向量,每种状态下样本个数为118(一半作为训练样本,一半作为检测样本),AS-VPMCD算法使用QI模型,r取10,j取10,故障分类和识别率如表2所示。 表3 滚动轴承VPMCD及AS-VPMCD故障识别率 改进前后的分类结果如图3、图4所示,由图3可知,3、4类中存在错误识别的故障样本,而3、4类故障均属于滚动轴承的滚动体故障,从原理上分析,滚动体受不完全约束,多一个旋转自由度,当我们通过电火花加工滚动体进行试验并进行数据采样时,滚动体与内外圈接触,随机自转可产生与其他类故障接近的振动信号,从而在分类过程中被误分为其他类别。第3、4类故障中,滚动体不完全约束产生的随机转动与高速列车的随机激励产生的故障信号突变相似。 图3 VPMCD识别结果Fig.3 Classification results of VPMCD 图4 AS-VPMCD识别结果Fig.4 Classification results of AS-VPMCD 分析表2、图3和图4的结果可知,本文通过样本关联,对突变点进行平滑性处理,能有效提高滚动轴承故障诊断识别率。 考虑高速列车非线性轮轨接触几何关系、非线性轮轨相互作用力以及非线性悬挂力,采用SIMPACK动力学仿真软件,对某型高速动车组进行了大量仿真实验,仿真实验记录了各状态下运行的高速列车车体、构架、轴箱上各部位的横向、纵向和垂向振动加速度和振动位移信号,共得到52个通道数据。 根据仿真实验结果,不同的通道对不同故障类型和故障部位的故障诊断各有侧重。本文为说明VPMCD改进算法,以横向作用的抗蛇行减振器故障、横向减振器故障等故障形式以及正常工况为例,采集时域和频域特征量,结合AS-VPMCD进行故障诊断。仿真时速为320 km/h,共采集了3.6 min的振动信号,采样频率为243 Hz。通过EEMD分解后提取IMF1~IMF6的频域特征重心频率、均方频率、频率方差组成的18维特征向量,将时长为3 s的数据作为一个样本,每种状态各取得72个样本(一半作为训练样本,一半作为检测样本)[6],AS-VPMCD算法使用QI模型,r取7,j取10。 图5 高速列车故障诊断识别率Fig.5 Fault diagnosis recognition rate of high speed train 运用原方法和本文改进方法分别对该数据进行故障诊断,52通道的综合识别率如图5所示。由图5可看出,对原方法识别率高于50%的通道,通过本文的故障诊断方法改进,识别率有明显提高。原识别率高于70%的通道1、通道2、通道9、通道11、通道39、通道41、通道50识别率有非常明显的提升,识别率均在95%以上,与原方法相比,识别率提高了20%以上。由于本改进方法通过相邻样本的识别结果对突变样本进行处理,对于故障信号严重混叠的情况,多数相邻故障样本无法正确辨识,故难以提高识别率低于50%的通道的识别率。 (1)针对原VPMCD算法对样本量的要求限制,本文通过滑窗逐步回归进行改进,使得算法在样本数较小的情况下仍然可以将每一维特征纳入分类算法中,在保证算法精度的同时,减小了算法对样本数量的依赖。 (2)实际故障诊断中,同一阶段输入的大部分样本数据是连续稳定的,小部分数据由于外界随机激励而产生了突变点。本文通过相邻样本关联,根据多个样本的识别结果作出最终分类,对突变样本进行了有效处理。 (3)运用SIMPACK动力学仿真,获取高速列车正常工况、抗蛇行减振器失效、横向减振器失效的数据,由本文改进方法识别结果分析可知,该方法有效提高了高速列车故障诊断的识别率。 (4)通过滑窗逐步回归和样本关联对VPMCD识别算法的改进,可将EEMD分解提取的特征量与VPMCD识别算法相结合的故障诊断方法用于高速列车等结构复杂、随机激励多的机械系统故障诊断。仅通过单一通道进行故障诊断,存在识别率较低、通道选择困难等问题,下一步将对通道组合和特征降维算法深入研究,以期进一步改进高速列车的故障诊断方法。 [1] 赵志宏. 基于振动信号的机械故障特征提取与诊断研究[D].北京:北京交通大学,2012. ZHAO Zhihong. Research on Vibration Signal Based Machinery Fault Feature Extraction and Diagnosis[D]. Beijing: Beijing Jiaotong University,2012. [2] 王靖. 列车轮对故障振动特性及诊断关键技术研究[D]. 长沙:中南大学, 2012. WANG Jing. Research of the Key Technologies for the Train’s Wheel Set Fault Vibriation Characteristics Diagnosis Method[D]. Changsha: Central South University, 2012. [3] 丁夏完,刘金朝,王成国.基于EMD和自适应STFT的货车滚动轴承故障诊断[J]. 中央民族大学学报(自然科学版), 2006, 26(3):253-258. DING Xiawan, LIU Jinzhao,WANG Chengguo.The EMD and Adaptive STFT Based Fault Diagnosis Method of Freight Locomative Rolling Bearing [J]. Journal of Central University for Nationalities (Natural Science Edition), 2006, 26(3): 253-258. [4] 陈特放,黄采伦,樊晓平. 基于小波分析的机车走行部故障诊断方法[J]. 中国铁道科学, 2005, 26(4):89-92. CHEN Tefang, HUANG Cailun, FAN Xiaoping. The Wavelet Analysis Based Fault Diagnosis Method of Locomotive Running Gear Fault [J]. China Railway Science, 2005, 26(4):89-92. [5] 马莉,傅八路,王泽勇,等.列车车轮踏面擦伤信号处理算法研究[J]. 铁道技术监督,2009,37(3):5-7. MA Li, FU Balu,WANG Zeyong, et al. The Study of Train Wheel Tread Scratches Signal Processing Algorithms[J]. Railway Quality Control ,2009,37(3):5-7. [6] 秦娜. 高速列车转向架故障的信息熵测度特征分析方法研究[D]. 成都:西南交通大学, 2014. QIN Na. Research on High-speed Train Bogie Fault Data Feature Analysis Method Based on Information Entropy Measuerment[D]. Chengdu: Southwest Jiaotong University, 2014. [7] WU Z H, HUANG N E. Nsemble Empirical Mode Decomposition: a Noise Assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2009,1(1):1-41. [8] RAGHURAJ R, LAKSHMINARAYANAN S. Variable Predictive Models-A New Multivariate Classification Approach for Pattern Recogintion Applications[J]. Patten Recogintion, 2009,42(1):7-16. [9] RAGHURAJ R, LAKSHMINARAYANAN S. Variable Predictive Model Based Classification Algorithm for Effective Separation of Protein Structural Classes[J]. Computational Biology and Chemistry, 2008, 32(4): 302-306. [10] 罗颂荣, 程军圣, 杨宇,等. 基于本征时间尺度分解和变量预测模型模式识别的机械故障诊断[J]. 振动与冲击, 2013, 32(13):43-48. LUO Songrong, CHENG Junsheng, YANG Yu, et al. Machine Fault Diagnosis Method Using ITD and Variable Predictive Model-based Class Discrimination[J]. Journal of Vibration and Shock, 2013,32(13):43-48. [11] 杨宇,李杰,潘海洋,等. 改进VPMCD方法在滚动轴承故障诊断中的应用[J]. 中国机械工程,2014,25(4): 491-496. YANG Yu, LI Jie, PAN Haiyang, et al. Application of Improved VPMCD Approach in Roller Bearing Fault Diagnosis[J]. China Mechanical Engineering, 2014, 25(4): 491-496. [12] 杨宇,李紫珠,何知义,等. 基于ASTFA降噪和AKVPMCD的滚动轴承故障诊断方法[J]. 中国机械工程, 2015, 24(21): 2934-2940. YANG Yu, LI Zizhu, HE Zhiyi, et al. The Rolling Bearing Fault Diagnosis Method Based on ASTFA De-noising and AKVPMCD[J]. China Mechanical Engineering, 2015, 24(21): 2934-2940. [13] 潘海洋,杨宇,李永国,等. 基于流形学习和改进VPMCD的滚动轴承故障诊断方法[J]. 振动工程学报, 2014, 27(6): 934-941. PAN Haiyang,YANG Yu, LI Yongguo, et al. A Rolling Bearing Fault Diagnosis Method Based on LE and KVPMCD[J]. Journal of Vibration Engineering, 2014, 27(6): 934-941. [14] 杨宇,潘海洋,程军圣.基于Kriging函数的KVPMCD在滚动轴承故障诊断中的应用[J]. 中国机械工程,2014,25(16):2131-2136. YANG Yu, PAN Haiyang, CHENG Junsheng. Applation of KVPMCD Based on Kriging Function in Rolling Bearing Fault Diagnosis[J]. China Mechanical Engineering, 2014, 25(16):2131-2136. [15] 朱明,吴思东,付克昌,等. 基于熵特征的高速列车故障诊断方法[J]. 振动、测试与诊断, 2015, 35(2):381-387. ZHU Ming, WU Sidong, FU Kechang. A High-speed Train Fault Diagnosis Method Based on Entropy Feature[J].Journal of Vibration, Measurement & Diagnosis, 2015, 35(2): 381-387. [16] 何晓群,刘文卿. 应用回归分析[M]. 北京:中国人民大学出版社,2011. HE Xiaoqun, LIU Wenqing. Applied Regression Analysis[M]. Beijing: China Renmin University Press,2011.3 改进故障诊断方法的验证
3.1 滚动轴承故障诊断
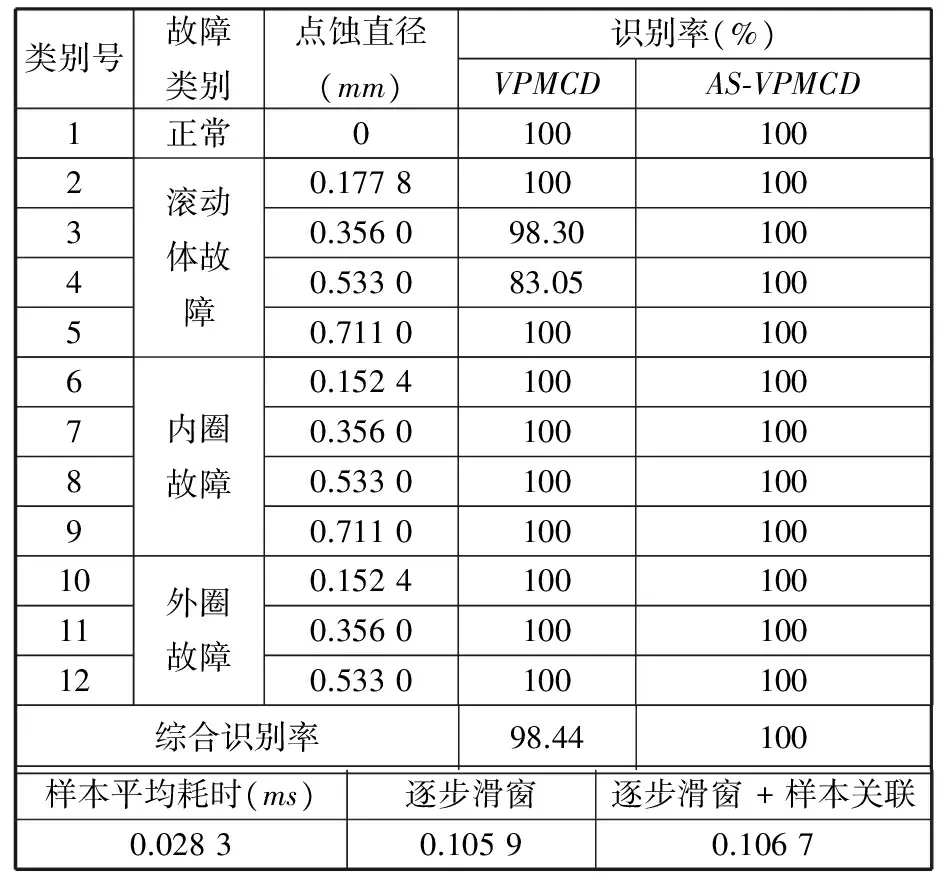
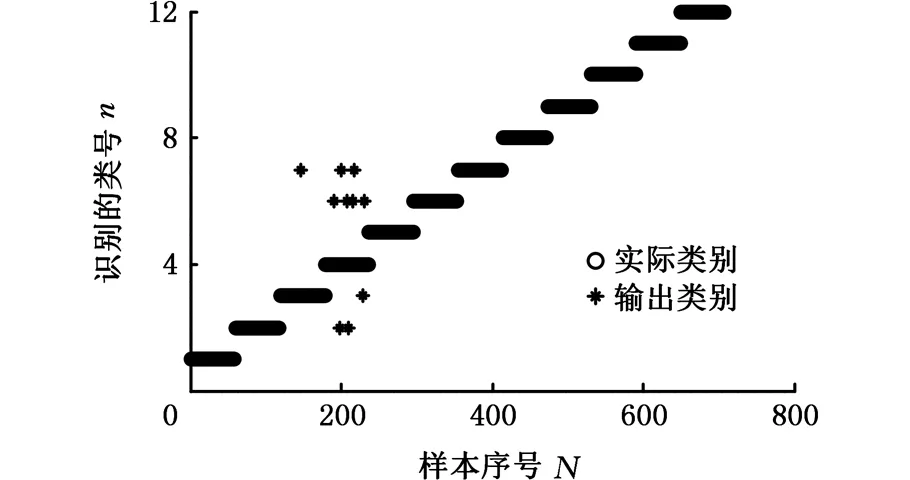
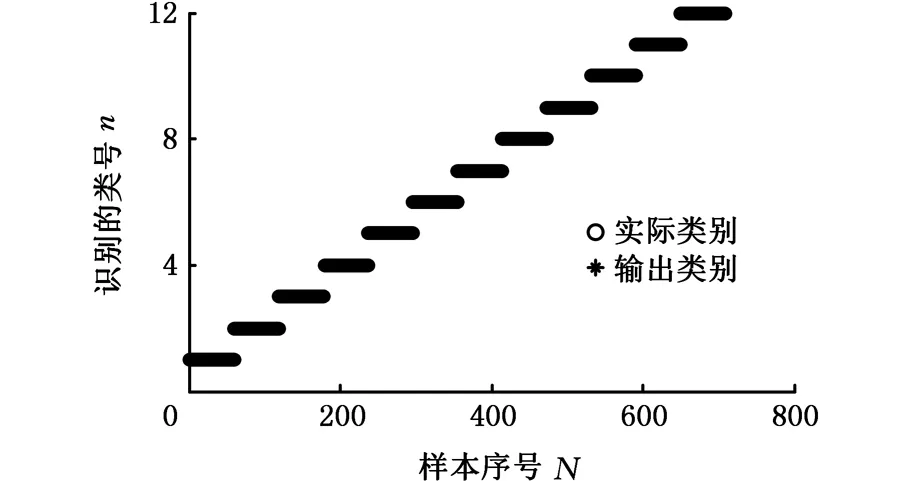
3.2 高速列车故障诊断
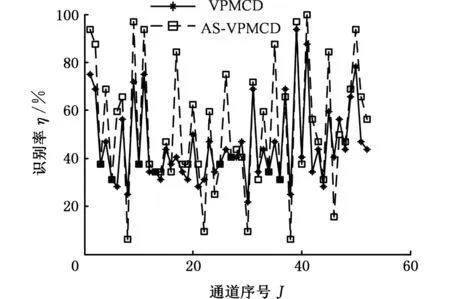
4 结论
