线图、 全图和细分图的第一几何-算数指数的上下界

霍英杰， 高玉斌

(中北大学 理学院， 山西 太原 030051)

0 引 言

拓扑指数通过分子结构数值化产生， 是一种具有反映化合物结构特征性质的图的不变量[1-2]. 近年来， 许多数学和化学工作者将研究重心放在研究特殊图类的某种拓扑指数这一课题上. 2009年, Vukicevic.D等[3]提出了图的第一几何-算数指数(简称GA1指数)的定义

(1)

式中：d(u),d(v)分别为顶点u和顶点v的度；E(G) 为G的边集.

由于GA1指数是一种提出时间不久的拓扑指数， 所以目前的研究成果较少. Das. K C等[4-5]研究了连通图GA1指数的一些上界和下界， 证明了界可达并刻画了相应极图. 刘克强等[6]给出一定边数的连通图中线图的GA1指标的上界或下界， 证明了这些界是可达的， 并刻画了相应的极图. Mahmiani A.等[7]给出一定边数及悬挂边数的连通图中全图的GA1指标的界. 线图、 全图、 细分图不仅是拓扑指数中重要的研究图类[1,8-9]， 而且在化学等方面有着广泛应用[1,10].

本文通过对不等式进行放缩的方法， 将特定边数的n阶连通图中线图、 全图的GA1指数的界推广到n阶连通图中线图、 全图及细分图的GA1指数的界， 得到了线图、 全图和细分图的上下界， 且刻画了达到上下界的极图.

文中所考虑的图G=(V(G),E(G))均为简单图， 其中V(G)是G的顶点集，E(G)是G的边集，d(v)为点v在图G中的度.

1 线图的GA1指数

令EL={(u1v,vu2)|u1v,vu2∈E(G)}, 称图(E(G),EL)为图G的线图， 记为L(G).dL(v)表示点v在图L(G)中的度.

由线图的定义可知dL(u1v)=d(v)+d(u1)-2，dL(vu2)=d(v)+d(u2)-2， 其中v,u1,u2∈V(G)，u1v,vu2∈E(G).

定理 1 设G是n阶连通图， 最大度为Δ， 最小度为δ， 且δ≥2， 则

(2)

等式成立当且仅当d(v)=d(u)，G为正则图.

证明 由式(1)知

(3)

由于δ≤d(v),d(u1),d(u2)≤Δ， 可得

即

且

又由于

故

(4)

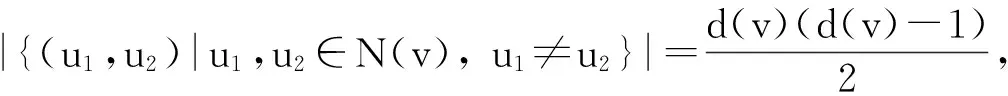
等式成立当且仅当d(v)=d(u)， G为正则图.

2 全图的GA1指数

令ET={(v,uv)|uv∈E(G)}， 称图T(G)=(V(G)∪E(G),E(G)∪EL∪ET)为图G的全图， 记为T(G). dT(v)表示点v在图T(G)中的度.

由全图的定义知， dT(v)=2d(v)， dT(uv)=d(u)+d(v)， 其中u∈V(G), uv∈E(G).

定理 2 设G为n阶连通图， 边数为m， 最大度为Δ， 最小度为δ， 且δ≥2， 则

(5)

等式成立当且仅当d(v)=d(u)， G为正则图.

证明 令

由全图的定义及式(1)知

GA1(T(G))=I1+I2+I3.

(6)

由于δ≤d(u)， d(v)≤Δ， 可得

即

且

又由于

故

综合上式可得

(7)

等式成立当且仅当d(u)=d(v).

同样， 仿照上面的证明方法， 还可以得到

(8)

(9)

故由式(6)～(9)可得到

等式成立当且仅当d(v)=d(u)，G为正则图.

3 细分图的GA1指数

将图G中每条边替换为P2(长为的路)后所得到的图称为G的细分图， 记为S(G).

定理 3 设G是连通图且边数为m， 最大度Δ， 则

(10)

右侧等式成立当且仅当G≅Cn.

且

又由于

故

(11)

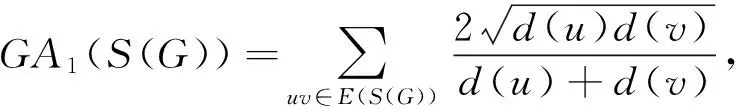
右边等号成立当且仅当d(v)=d(u)=2， G≅Cn.

定理 4 设G为n阶连通图， 最大度为Δ， 最小度为δ， 则

nΔ(Δ-1),

右边等号成立当且仅当G≅Cn.

证明 由定理3及线图的定义可知

且

由于

(12)

故

nΔ(Δ-1),

右边等号成立当且仅当G≅Cn.

定理 5 设G是n阶连通图， 边数为m， 最大度为Δ， 最小度为δ， 则

GA1(S(T(G)))≤6m+nΔ(Δ-1),

右边等号成立当且仅当G≅Cn.

证明 由定理3及全图的定义可知

GA1(S(T(G)))≤2(|E(G)|+|EL|+|ET|),

|E(G)|+|EL|+|ET|=m+

由式(12)易知结论成立.

[1]GutmanI，EstradaE.Topologicalindicesbasedonthelinegraphofthemoleculargraph[J].JournalofChemicalInformationandComputerSciences， 1996， 36(3)： 541-543.

[2]TodeschiniR，ConsonniV.Handbookofmoleculardescriptors[M].Weinheim：Wiley-VCHVerlag， 2000.

[3]VukicevicD，FurturcaB.Topologicalindexbasedontherationsofgeometricalandarithmeticalmeansofend-vertexdegreesofedges[J].JournalofMathematicalChemistry， 2009， 46(4)： 1369-1376.

[4]DasKC.Ongeometric-arithmeticindexofgraphs[J].Match-CommunicationsinMathematicalandinComputerChemistry， 2010， 64(3)： 619-630.

[5]DasKC，GutmanI，FurtulaB.Onthefirstgeometric-arithmeticindexofgraph[J].DiscreteAppliedMathematics， 2011， 159(17)： 2030-2037.

[6]刘克强， 赵飚. 线图的几何-算数指标[J]. 江苏师范大学学报(自然科学版)， 2014， 32(4)： 26-30.LiuKeqiang，ZhaoBiao.Ongeometric-arithmeticindexoflinegraph[J].JournalofJiangsuNormalUniversity(NaturalScienceEdition)， 2014， 32(4)： 26-30. (inChinese)

[7]MahmianiA，KhormaliO.Onthetotalversionofgeometric-arithmeticindex[J].MathematicalChemistry， 2013， 4(1)： 21-26.

[8]ChenZQ，MengJX，TianYZ.Onatom-bondconnectivityindexoflineandtotalgraphs[J].OperationsResearchTransactions， 2013， 17(3)： 1-10.

[9]孙晓玲， 高玉斌， 杜建伟. 线图、 全图和细分图的augmentedZagreb指数[J]. 中北大学学报(自然科学版)， 2015， 36(1)： 1-4.SunXiaoling，GaoYubin，DuJianwei.AugmentedZagrebindexofline，totalandsubdivisiongraphs[J].JournalofNorthUniversityofChina(NaturalScienceEdition)， 2015， 36(1)： 1-4. (inChinese)

[10]GutmanI，Popovic，MishraBK，etal.Applicationoflinegraphsinphysicalchemistry[J].JournaloftheSerbianChemicalSociety， 1997， 62(11)： 1025-1029.