一种高动态环境巡飞器姿态快速解算算法研究

王梦龙， 王 洋， 王 华

(1. 北京航空航天大学 宇航学院， 北京 100191； 2. 北京自动化控制设备研究所， 北京 100074)

0 引 言

捷联惯性导航系统一般固连在载体上， 直接测量载体的运动， 而姿态实时解算是捷联惯性导航系统工程应用中需要解决的关键技术[1-6]. 巡飞器在飞行过程中需要经常做转弯和盘旋等高动态机动动作， 在这种高动态环境中， 巡飞器姿态解算必然会产生不可交换性误差， 特别是当巡飞器做圆锥运动时产生的不可交换性误差最大， 也称为圆锥误差[7-10]. 此时要得到高精度的姿态角， 必须对圆锥误差进行补偿， 所以高动态环境下圆锥误差补偿对巡飞器实时姿态解算精度的提高有重要意义. 为了减小圆锥误差的影响， Bortz首次提出了等效旋转矢量概念[11]， 此后国内外学者对此作了大量研究. 文献[12]提出了一种基于角增量的改进高动态捷联惯导解算算法， 文献[13]提出了一种双速优化姿态编排算法， 文献[14]提出了一种旋转矢量多迭代捷联姿态计算误差补偿算法， 文献[15]采用角速率分析方法推导了一种简单新四子样算法， 这种方法为改进角速率输入下的旋转矢量算法提供了一种新的思路.

本文从工程实用的角度出发， 针对高动态环境中巡飞器姿态信息实时解算的特点， 提出了一种基于滑动三周期旋转矢量的姿态滤波算法. 最后通过数字仿真和飞行动态试验验证了该算法的有效性.

1 基于角速率的等效旋转矢量法

传统的姿态更新算法往往采用角增量计算等效旋转矢量， 这种方法应用于角速率输出陀螺仪， 需要先用数值积分法将角速率信息转换为角增量信息， 这样必然会引入积分计算误差.

根据Bortz理论[11,16]， 等效旋转矢量微分方程如下

(1)

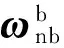
由于姿态解算周期一般较短， |Φ|的数值很小，Φ的高次幂可以忽略， 因此可得到工程中常用近似的等效旋转矢量微分方程为

(2)

对式(2)在姿态更新周期T上进行积分， 得到时间T内等效旋转矢量增量为

ΔΦ=α+e,

(3)

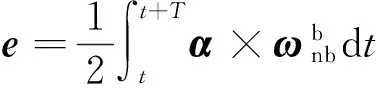
在姿态更新周期T内， 假设载体角速度可以由三次多项式拟合表示如下

(4)

式中：t为当前时刻；τ为到t时刻的时间间隔；a、b、c、d为多项式系数.

若将每个姿态更新周期T分为三等份， 并在每个等分时间点采样对应的角速率， 则在时间区间[t,t+T]内得到4个角速率， 按照时间从前至后的顺序依次对应ω1,ω2,ω3,ω4， 将其代入式(4)可得多项式系数如下

(5)

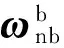
α=aT+bT2+cT3+dT4.

(6)

根据式(4)， 可得t时刻Φ的各阶导数为

(7)

将式(5)～(7)代入Φ(t+T)在t时刻的泰勒展开式， 得到基于角速率输入的等效旋转矢量在时间区间[t,t+T]上增量的估计表达式为

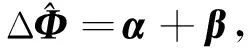
(8)

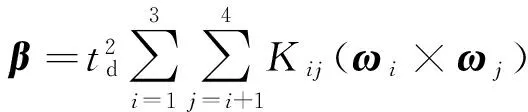
算法以4个连续的采样角速率作为输入计算一个姿态更新周期内的等效旋转矢量增量.

设巡飞器沿OL轴作如图 1 所示的典型圆锥运动， 图中OXYZ为参考坐标系；Oxyz是载体坐标系， 则其等效旋转矢量为

Φ(t)=[0γcos(ω0t)γsin(ω0t)]T,

(9)

式中：γ为锥半角；ω0为角频率.

将式(9)转化为四元数表示， 并通过四元数微分方程可得典型圆锥运动下载体坐标系相对于导航坐标系的角速率如下

(10)

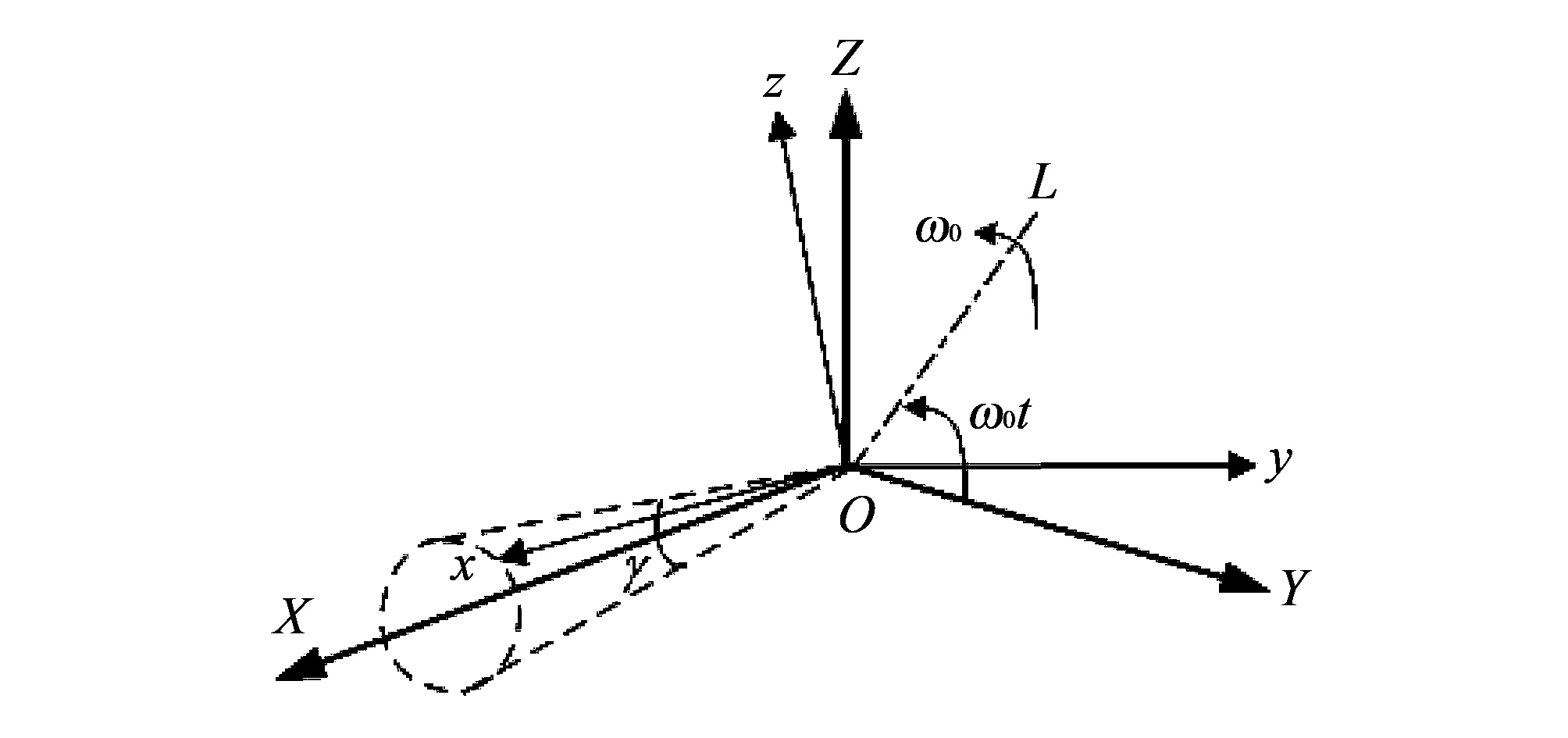
图 1 典型圆锥运动示意图Fig.1 Diagram of typical coning motion

将式(10)代入式(3)得到时间T内等效旋转矢量增量理论值为

(11)

由于周期震荡不会造成误差在时间上的累积， 故仅分析x轴上的算法误差. 将式(9)代入式(3)可以得到典型圆锥运动中载体x轴圆锥误差项真实值e为

e=2sin2(γ/2)(ω0T-sin(ω0T)).

(12)

令λ=ω0td， 则在典型圆锥环境下有

(13)

由式(13)计算圆锥误差计算值β， 并在t时刻进行Taylor展开

(14)

式中：K1=K12+K23+K34，K2=K13+K24，K3=K14.

同样对式(12)圆锥误差理论值在t时刻进行Taylor展开

(15)

令圆锥误差计算值β等于圆锥误差理论值e， 并忽略λ的高次项可得

(16)

将式(16)代入式(8)即可得到基于角速度三周期圆锥补偿旋转矢量算法

(17)

基于角速度三周期圆锥补偿旋转矢量误差估计值为

(18)

将式(14)，(15)代入式(18)， 并忽略高阶小量可得

(19)

2 滑动三周期旋转矢量更新算法

在相同动态环境中， 随着采样周期的增加， 多周期旋转矢量更新算法的精度会增加， 但算法姿态更新的频率却降低了， 影响了整个系统的实时性. 针对巡飞器这类对飞行器姿态更新频率要求较高的飞行器， 本文提出了一种滑动三周期旋转矢量更新算法， 有效结合了单周期算法更新速率快和三周期算法计算精度高的优点. 算法以连续两个单周期算法作为启动项， 在第三个周期后采用三周期算法解算巡飞器的姿态角， 从而实现姿态的快速更新.

假设系统一个姿态更新周期T内的采样点个数为N， 则载体的角速率采样周期td=T/N. 单周期旋转矢量更新算法、 三周期旋转矢量更新算法以及滑动三周期旋转矢量更新算法的载体角速率采样周期和姿态更新周期如图 2 所示.

图 2 姿态更新周期与采样周期关系示意图Fig.2 Diagram of relationship between attitude update period and sampling period

由图 2 可知， 滑动三周期旋转矢量算法的姿态角更新频率是普通三周期旋转矢量算法的3倍. 滑动三周期旋转矢量算法采用单周期旋转矢量法作为启动算法， 在前2个姿态采样周期采用单周期旋转矢量法， 可以由式(20)得到第1个采样周期末t1时刻的姿态变化四元数.

(20)

(21)

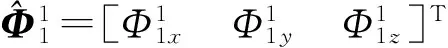
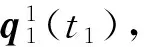
(22)

式中：Q(t0)为初始时刻t0的初始姿态四元数.

同理， 可由单周期旋转矢量法得出t2时刻的姿态更新四元数Q(t2)

(23)

(24)

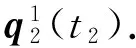
(25)

此时， 利用前2个采样周期的计算结果及采样数据， 在第3个采样周期末t3时刻， 采用三周期旋转矢量法计算t3时刻的姿态更新四元数Q(t3)， 采用三周期旋转矢量法时，T=3td.

(26)

(27)

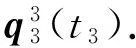
(28)

类似的， 按照式(26)～(28)可计算t3时刻之后各时刻的姿态更新四元数

(29)

由上述推导可以得出， 本文提出的滑动三周期旋转矢量姿态更新算法需要在前2个陀螺仪采样周期内采用单周期旋转矢量算法启动， 算法启动后的每个陀螺仪采样周期末都可以利用之前连续3个陀螺仪采样周期内的测量和计算数据， 按照上述提出的滑动三周期旋转矢量姿态更新算法依次计算出各个陀螺仪采样周期内的姿态更新四元数， 从而实时更新巡飞器的姿态信息. 由理论推导可知， 本文提出的滑动三周期旋转矢量算法在更新频率上与单周期算法持平， 高于双周期与三周期算法.

3 基于滑动三周期旋转矢量的姿态滤波算法

3.1 状态方程

扩展卡尔曼滤波器的误差状态量选取如下

(30)

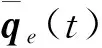
值得注意的是，在我国当时的民事法律及司法解释中尚无隐私权保护的规定，因此当事人在民事法律上主张住宅方面的隐私权受侵害，并要求法律予以保护，缺乏充分的立法依据。二审法院大胆援用我国宪法关于住宅不受侵犯的规定，从中引申出住宅隐私权的内容，从而对当事人的隐私权加以保障。二审法院对新兴权利的论证思路是，首先从我国宪法第39条第一句关于住宅不受侵犯的规定出发，认定住宅体现了个人领域，进而认定住宅的私密性属于隐私权，应受法律保护。

(31)

式中：α为机动频率；w(t)为白噪声.

姿态角误差方程忽略地球表观运动角速度， 以式(30)为状态量的状态方程为

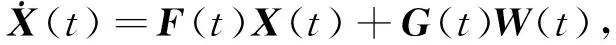
(32)

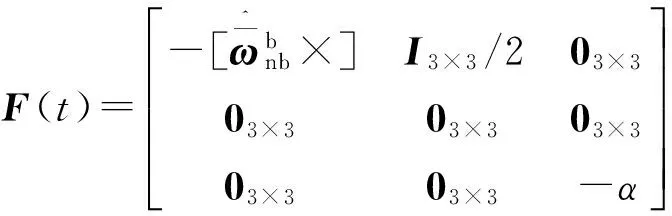
3.2 量测方程

选取加速度计的输出值与加速度估计值的差值以及地磁传感器的输出值与地磁向量在载体坐标系中的投影的差值作为观测量. 其中， 加速度估计值包含载体机动加速度估计值和重力加速度向量在载体坐标系中的投影， 系统的观测方程为

Z(t)=H(t)X(t)+V(t),

(33)

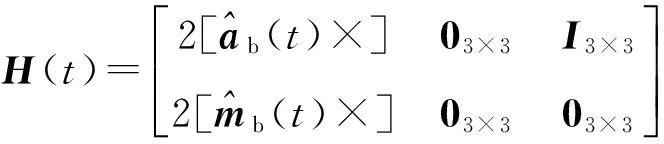
在每个采样周期内， 利用滑动三周期旋转矢量算法更新航向姿态四元数， 系统误差状态及协方差时间更新过程如下

(34)

量测更新方程为

(35)

4 试验结果

为验证本文基于滑动三周期旋转矢量的姿态滤波算法在工程实践中的有效性， 分别进行了数字仿真试验和动态飞行试验.

4.1 数字仿真试验

定点盘旋是巡飞器在执行侦查任务过程中一种常见的飞行状态， 这种飞行状态与典型的圆锥运动类似. 本组数字仿真通过模拟巡飞器在空中的定速定点盘旋飞行状态来验证本文基于滑动三周期旋转矢量的姿态滤波算法的有效性. 仿真盘旋半径为600 m， 高度为200 m， 飞行速度20 m/s， 滚转角为20°， 俯仰角为0°， 总仿真时间为250 s. 分别采用算法1： 单周期旋转矢量滤波算法； 算法2： 四元数四阶龙格库塔滤波算法； 算法3： 基于滑动三周期旋转矢量的姿态滤波算法3种算法估计巡飞器飞行过程中的姿态角误差.

如图 3 所示， 巡飞器首先向东匀速直线飞行60 s， 随后切入匀速盘旋飞行模式. 仿真计算结果如图 4， 表 1 和表 2 所示.

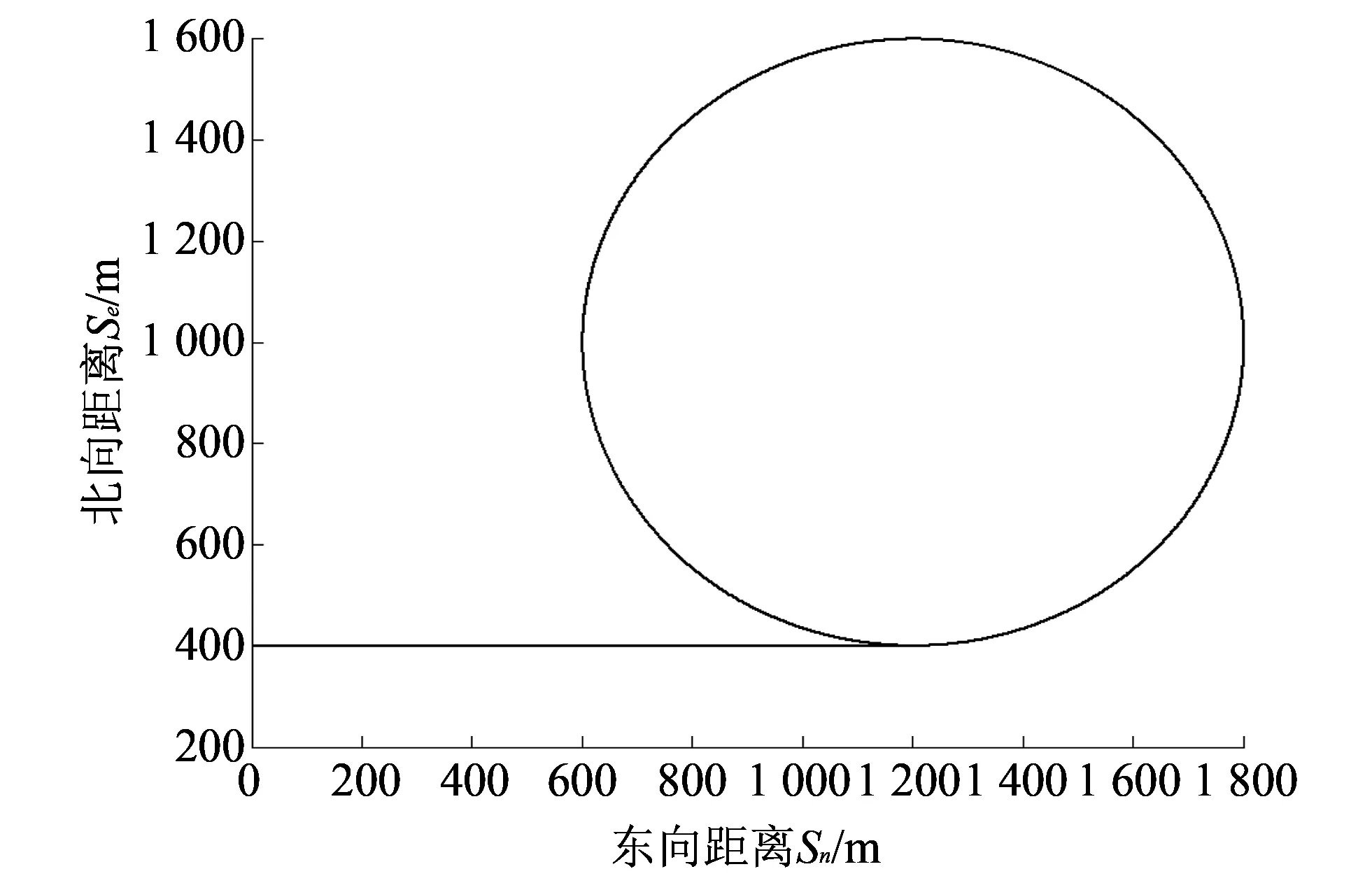
图 3 盘旋飞行轨迹Fig.3 Flight path of circling flight

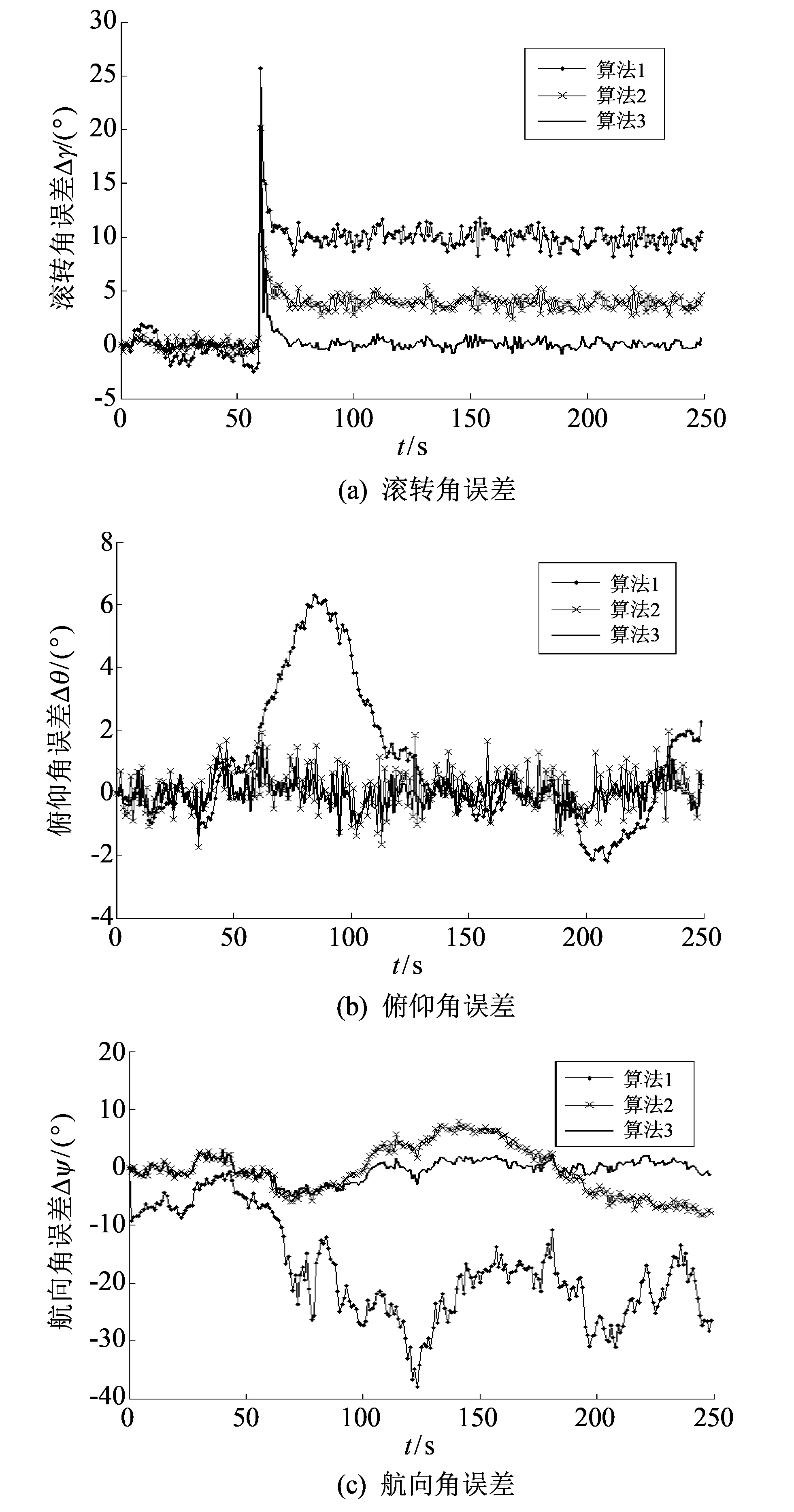
图 4 航向姿态角估计误差Fig.4 Estimated error of heading and attitude angle

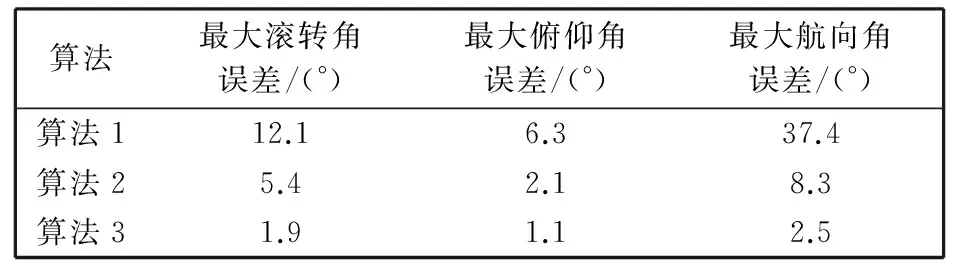
算法最大滚转角误差/(°)最大俯仰角误差/(°)最大航向角误差/(°)算法112.16.337.4算法25.42.18.3算法31.91.12.5

表 2 各算法姿态更新周期

通过图 4 可以看出， 在巡飞器由匀速水平飞行切入到匀速定点盘旋飞行模式后， 由于巡飞器的运动状态类似于典型的圆锥运动， 导致航向姿态角解算误差有一定幅度的增加， 尤其是受圆锥运动影响最大的航向角通道. 由表 1， 表 2 数据可以看出算法3的航向姿态角最大误差约为算法2的1/2， 仅为算法1的1/10， 且算法3的姿态更新周期与算法1相同， 仅为算法2的1/2.

4.2 飞行动态试验

为了验证本文基于滑动三周期旋转矢量的姿态滤波算法的飞行动态性能， 本文选用荷兰XSENS公司的MTI微惯性测量单元作为航向姿态角的参考基准. MTI的性能参数如下： 采样频率为100 Hz， 滚转角及俯仰角静态测量精度<0.5°， 航向角静态测量精度<1°， 动态测量精度为2° RMS.

利用巡飞器试验平台搭载MTI模拟执行侦察任务， 巡飞器在空中做定点盘旋飞行， 飞行实验平台及飞行轨迹如图 5， 图 6 所示. 利用MTI加速度计、 陀螺仪和地磁传感器原始数据， 采用同数字仿真试验中相同的3个算法解算巡飞器航向姿态角， 最后将解算结果与MTI航向姿态角输出值做比对得到误差角. 飞行动态试验结果如表 3 和图 7 所示.

图 5 巡飞器试验平台Fig.5 Loitering vehicle test platform

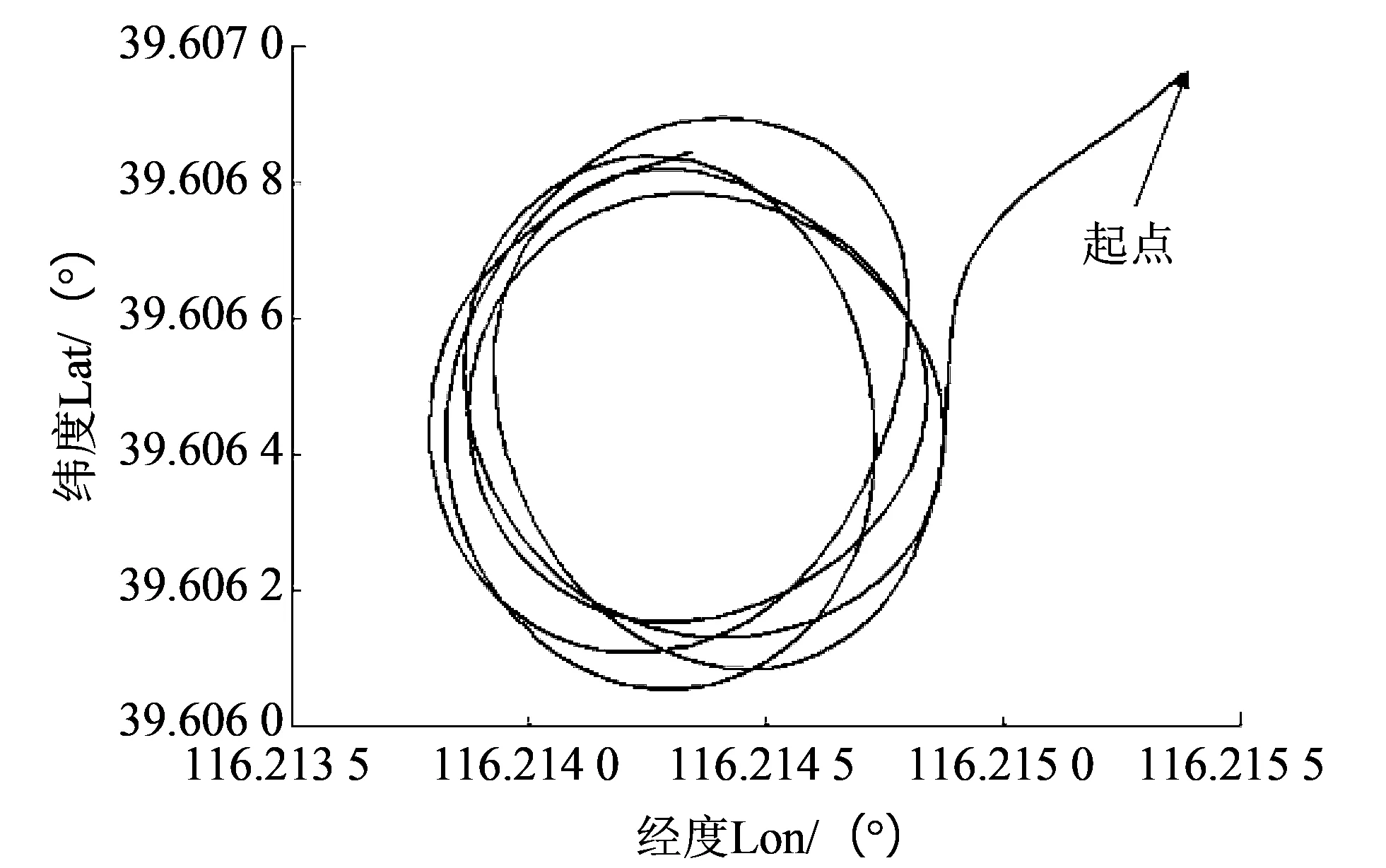
图 6 试验飞行轨迹Fig.6 Flight path of dynamic flight test

图 7 航向姿态角估计误差Fig.7 Estimated error of heading and attitude angle

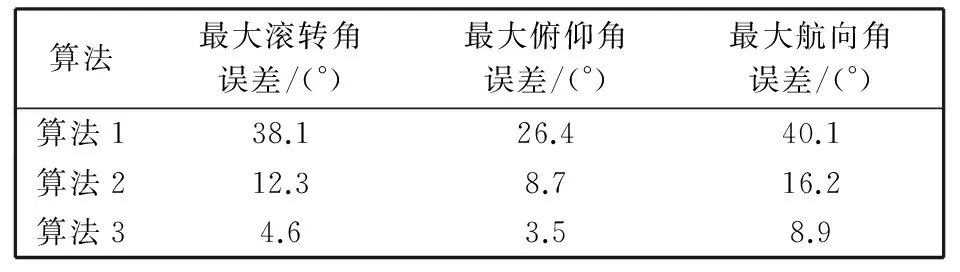
算法最大滚转角误差/(°)最大俯仰角误差/(°)最大航向角误差/(°)算法138.126.440.1算法212.38.716.2算法34.63.58.9

巡飞器做定点盘旋时一直处于高动态环境中， 此时巡飞器的飞行状态类似于典型的圆锥运动. 由图7和表3数据可已看出， 算法1由于采用了对圆锥误差抑制效果较弱的单周期旋转矢量算法， 从而导致其航向姿态角解算误差最大， 特别是受圆锥运动影响最大的航向角通道， 其解算误差达到了40.1°. 采用龙格库塔法的算法2的航向角解算误差为16.2°， 采用滑动三周期旋转矢量算法的算法3的航向角解算误差为8.9°. 此时算法3的航向姿态角解算误差约为算法2的1/2， 且仅约为算法1的1/7. 上述动态飞行试验结果验证了本文基于滑动三周期旋转矢量的姿态滤波算法的稳定性及有效性， 在动态飞行过程中具有较好的航向姿态角解算精度.

5 结 论

本文从工程实用的角度出发， 对现有几种姿态更新算法进行分析和比较， 详细推导得出了角速率输入的等效旋转矢量算法， 并提出了一种基于滑动三周期旋转矢量的姿态滤波算法. 通过仿真及试验将本算法与其他两种常用的姿态更新算法对比， 证实了基于滑动三周期旋转矢量的姿态滤波算法的合理性， 有效地解决了计算精度与计算周期的矛盾.

数字仿真及试验结果表明：

1) 该算法有效地补偿了系统的圆锥误差， 其误差角仅为单周期旋转矢量算法的1/7， 且明显优于四元数四阶龙格库塔算法.

2) 该算法的姿态更新周期仅为普通三周期旋转矢量法的1/3， 弥补了常规旋转矢量姿态更新算法存在的更新频率较低的问题.

3) 该算法的动态性能可以满足巡飞器等高动态飞行器的应用需求.

[1]李海涛， 曹咏弘， 祖静. 等效旋转矢量法在旋转弹姿态解算中的应用[J]. 测试技术学报， 2011， 25(4)： 287-291. Li Haitao, Cao Yonghong, Zu Jing. Application of rotation vector algorithm to attitude updating for spinning projectiles[J]. Journal of Test and Measurement Technology, 2011, 25(4)： 287-291. (in Chinese)

[2]程承， 潘泉， 李汉舟. 一种新的捷联惯导系统圆锥误差补偿算法研究[J]. 弹箭与制导学报， 2014， 34(1)： 1-4. Cheng Cheng, Pan Quan, Li Hanzhou. The research on new coning error compensation algorithm for strapdown inertial navigation system[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2014, 34(1)： 1-4. (in Chinese)

[3]Maley J M. Efficient attitude estimation for a spin-stabilized projectile[J]. Journal of Guidance Control and Dynamics, 2016, 39(2)： 339-350.

[4]Weibel D, Lawrence D, Palo S. Small unmanned aerial system attitude estimation for flight in wind[J]. Journal of Guidance Control and Dynamics, 2015, 38(7)： 1300-1305.

[5]Chen J Z, Yuan J P, Fang Q. Flight vehicle attitude determination using the modified rodrigues parameters[J]. Chinese Journal of Aeronautics, 2008, 21(5)： 433-440.

[6]Gebre-Egziabher D, Hayward R C, Powell J D. Design of multi-sensor attitude determination systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2004, 40(2)： 627-649.

[7]严恭敏， 杨小康， 翁浚， 等. 一种求解不可交换误差补偿系数的通用方法[J]. 宇航学报， 2017， 38(7)： 723-727. Yan Gongmin, Yang Xiaokang, Weng Jun, et al. A general method to obtain noncommutativity error compensation coefficients for strapdown attitude algorithm[J]. Journal of Astronautics, 2017, 38(7)： 723-727. (in Chinese)

[8]Savage P G. Strapdown inertial navigation integration algorithm design part 1： attitude agorithms[J]. Journal of Guidance Control and Dynamics, 1998, 21 (1)： 19-28.

[9]严恭敏， 杨小康， 翁浚， 等. 捷联惯导中求解圆锥误差系数的通用算法[J]. 导航定位学报， 2017， 5(3)： 1-5. Yan Gongmin, Yang Xiaokang, Weng Jun, et al. A general numerical method to obtaining optimized coning compensation coefficients for strapdown attitude algorithm[J]. Journal of Navigation and Positioning, 2017, 5(3)： 1-5. (in Chinese)

[10]Lee J G, Yoon Y J, Mark J G, et al. Extension of strapdown attitude algorithm for high-frequency base motion[J]. Journal of Guidance Control and Dynamics, 1990, 13 (4)： 738-743.

[11]Bortz J E. A new mathematical formulation for strapdown inertial navigation[J]. Journal of IEEE Transactions on Aerospace and Electronic Systems, 1971, 7(1)： 61-66.

[12]赵欣， 王仕成， 杨东方， 等. 一种改进的高动态捷联惯导解算算法[J]. 中国惯性技术学报， 2011， 19(2)： 163-169. Zhao Xin, Wang Shicheng, Yang Dongfang, et al. Improved algorithm for high dynamic strapdown inertial navigation system[J]. Journal of Chinese Inertial Technology, 2011, 19(2)： 163-169. (in Chinese)

[13]邢丽， 熊智， 刘建业， 等. 针对高动态载体应用的高精度捷联惯导姿态算法优化方法[J]. 中国惯性技术学报， 2014， 22(6)： 701-706. Xing Li, Xiong Zhi, Liu Jianye, et al. Optimized method of high-precision attitude algorithm for high dynamic vehicles[J]. Journal of Chinese Inertial Technology, 2014, 22(6)： 701-706. (in Chinese)

[14]王真， 高凤岐， 高敏， 等. 旋转矢量多迭代捷联姿态解算误差补偿算法[J]. 中国测试， 2016， 42(8)： 113-117. Wang Zhen, Gao Fengqi, Gao Min, et al. Research on error compensation improved algorithm of strapdown attitude & heading measurement based on multiple iteration rotation vector[J]. China Measurement & Test, 2016, 42(8)： 113-117. (in Chinese)

[15]黄昊， 邓正隆. 角速率输入下的航姿算法研究[J]. 中国惯性技术学报， 2002， 10(8)： 9-14. Huang Hao, Deng Zhenglong. Study of navigation attitude algorithms for angular rate input[J]. Journal of Chinese Inertial Technology, 2002, 10(8)： 9-14. (in Chinese)

[16]Wu Y X, Hu X P, Hu D W, et al. Strapdown inertial navigation system algorithms based on dual quaternions[J]. Journal of IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(1)： 110-132.