辗转相除法的统一公式及其应用
2018-02-05魏春强
杨 妮,魏春强
(安康学院 数学与统计学院,陕西 安康 725000)
1 统一公式
对于P[x]中任意两个多项式f(x)与g(x),其中g(x)≠0,f(x)g(x),由辗转相除法可以得到下面的等式:

于是可得
定理1(统一公式)对于P[x]中任意两个多项式 f(x)与 g(x),g(x)≠0,f(x)>g(x),则

证明用数学归纳法。当k=1时,定理1成立,由辗转相除法开始的两个等式,有
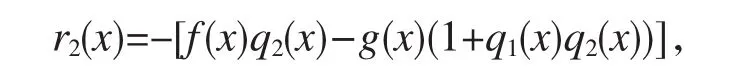
由于

即定理1对k=2成立。
假定命题对正整数1,2,…,k都成立,现在证明对k+1也成立。
2018年10月16日,农业农村部副部长于康震赴辽宁省锦州市北镇市现场指导非洲猪瘟疫情处置并组织召开东北三省非洲猪瘟防控工作现场会。于康震强调,要充分认识当前复杂严峻的疫情形势,把规模化养猪场和种猪场“两场”的疫病防控工作摆在更加突出的位置,统筹疫病防控和产业发展,采取有力措施,切实保护好生猪产业和市场供给的基础。

由此,对一切k(k=1,2,…,n),定理1的结论成立。
同理可证明,对于P[x]中任意两个多项式f(x)与 g(x),f(x)≠0,f(x) 定理2[1]13对于P[x]中任意两个多项式f(x)与g(x),最大公因式是d(x),则存在多项式u(x),v(x),使得f(x)u(x)+g(x)v(x)=d(x)成立。 由定理1我们给出新证法。 证明当g(x)=0时,f(x)与g(x)的最大公因式为 当g(x)≠0时,不妨设f(x)>g(x),由定理1的证明可知d(x)=rn(x), 由上式得 在实际应用中,经常需要计算定理2中的多项式u(x)与v(x),而传统的回代法求u(x)与v(x)的计算过程往往比较繁琐。若通过辗转相除法的统一公式,借助列表法求定理2中的多项式u(x),v(x),可明显减少计算量。 通过仔细观察,我们可以将统一公式通过列表进行计算:先把q1(x),q2(x),…,qn(x),写入表的第二行,再在表的第二及第三列写入M0(x)=1,Q0(x)=0,M1(x)=q1(x),Q1(x)=1,然后根据 Mk(x)=qk(x)Mk-1(x)+Mk-2(x),Qk(x)=qk(x)Qk-1(x)+Qk-2(x),顺次求出 M2(x),Q2(x),M3(x),Q3(x),…,Mn(x),Qn(x)。表中的“+”号连接qk(x)到Mk-1(x),Qk-1(x)的线及箭头“→”可以帮助我们记忆,最后在Mn(x),Qn(x)前分别乘上(-1)n-1与(-1)n就得所求的u(x)与v(x)。列表如下: 下标i0 1 2 … k-2 k-1 k… n qi(x) q1 q2…qk-2qk-1 qk…qn Mi(x)1 qM2…Mk-2Mk-1Mk…Mn Qi(x)0 1Q2…Qk-2Qk-1Qk…Qn 例1[2]求f(x)=4x4-2x3-16x2+5x+9与g(x)=2x3-x2-5x+4的最大公因式d(x),并求出u(x),v(x),使得 f(x)u(x)+g(x)v(x)=d(x)。 解法一用传统回代法。 由 于是 故 解法二用统一公式法。 由定理2知 列表如下: 下标i 0 1 2 qi(x) 2x -1 Mi(x) 1 2x -2 3x+1 Qi(x) 0 1 -1 3x+1 3 3x2+2 3x+1 3 总结:对比解法一和解法二,我们可以看出,采用统一公式法求解u(x)和v(x)更方便快捷,计算量小,准确度高,而传统的回代法求解u(x)和v(x)过程繁杂,也容易出错。 例2[1]45求f(x)=x4+2x3-x2-4x-2与g(x)=x4+x3-x2-2x-2的最大公因式d(x),并求出u(x),v(x),使得f(x)u(x)+g(x)v(x)=d(x)。 解用统一公式法。 由定理2知 列表如下: ? 本文结合辗转相除法与列表法,总结出用辗转相除法求最大公因式相关的多项式u(x)和v(x)的统一公式,为求解u(x)和v(x)提供了简便途径。不但简化了计算量,而且条理清晰,过程简洁,一目了然,特别对求解u(x)和v(x)的步骤较多的题目,采用统一公式法求解比传统的回代法更有优势,规避了传统的回代法步骤较多,过程繁杂,运算量大,极易出错的弊端。 [1]王萼芳,石生明.高等代数[M].北京:高等教育出版社,2003. [2]李金坤.高等代数同步辅导及习题全解[M].4版.北京:中国水利水电出版社,2015:15.


2 应用






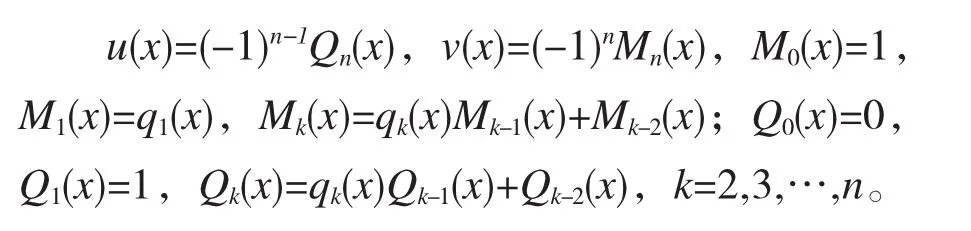





3 结语
