借助转化的数学思想

李剑

摘要：数学教学中必须重视思想方法的教学，它是数学教育教学本身的需要，是以人为本的教育理念下培养学生素养为目标的需要，是提高学生解题能力的需要。小学数学教学中要求教师重视并掌握各章节中蕴含的数学思想方法；要重视基本知识、基本技能的教学，并渗透数学思想方法；要引导促进学生对数学思想方法的内化；在循环教学中及时总结，明确介绍和突出体现某种思想方法，使学生对这一数学思想和数学方法得到强化和巩固。

关键词：转化思想；学生；数学学习能力

中图分类号：G633.6 文献标识码：A 文章编号：1992-7711（2017）10-0007

数学思想蕴含在数学知识形成、发展和应用的过程中，是数学知识和方法在更高层次上的抽象与概括，如抽象、演绎、分类、归纳、模型、转化等。而转化思想是解决数学问题的一种最基本的数学思想，在研究数学问题时，通常是将未知问题转化为已知的问题，将复杂的问题转化为简单的问题，将抽象的问题转化为具体的问题，将实际问题转化为数学问题，也常常在不同的数学问题之间互相转化，可以说在解决数学问题时转化思想几乎是无处不在的。

一、转化思想在数学教学中的价值

1. 转化思想在数学教学中的地位和价值

（1）《数学课程标准》的期待

《数学课程标准》（最新稿）不仅把“数学思考”作为总体目标之一提出，同时还将“双基”扩展为“四基”，即基础知识、基本技能、基本数学思想、基本活动经验。由此可见，数学思想方法教学变得越来越重要。

（2）数学教育专家的观点

全国数学特级教师徐斌老师说：比知识重要的是方法，比方法更重要的是思想。在小学数学教学中，数学知识本身非常重要，但真正对学生以后的学习、生活和工作起长期作用，并使其终身受益的是数学思想方法。日本数学家米山国藏指出：“无论是对于科学工作者、技术人员，还是数学教育工作者，最重要的就是数学的精神、思想和方法，而数学知识只是第二位”。

2. 小学数学学科特点

（1）小学数学是学生自己的数学

小学数学知识是学生借助已有的生活经验通过具体活动产生的；数学教学要向学生提供探索、讨论、实践、调查和解决问题的各种机会，其基本方式不应该是“授予”，而是“引导”，给学生的思考和发展留下充分的空间，使学生真正成为学习活动的主人；数学学习不再是单纯的记忆、模仿和训练，而是自主探索、合作交流与实践创新等多种形式的学习；数学课堂应由单纯的知识传授的殿堂转变为学生主动从事数学活动的场所；数学教师应由单纯的知识传授者转变为学生数学学习的组织者、引导者和合作者。

（2）小学数学是生活化的数学

从儿童的生活经验来看，数学学习不再是局限于教室中的活动，而且是一种社会性的活动。学生的生活环境及任何一个活动场所都应该作为数学学习的课堂。校外的买卖活动、房屋的建造备料、面积的估计测量都含有丰富的数学问题和知识。学生数学学习的内容应当是现实的、生活化的、有趣的和富有挑战性的。这些内容有利于学生观察、实验、猜测、验证、推理、交流等能力的培养。

3. 小学生的学习特点

（1）小学生的认知规律

小学生的认知规律是由具体向抽象、由低级向高级发展的过程。但到了四年级以后，其认知带有很强的形象性和具体性，所以教育学生应该考虑这些特点，通过学习兴趣的激发，通过获得成功体验的过程来调动孩子学习的积极性。

（2）小学生的学习习惯

学习习惯是指学生在长期的学习实践过程中逐渐形成的不需要意志努力和监督的自动化行为倾向。学习习惯有好坏之分，如：课前预习、上课专心听讲，认真完成作业等都是良好的学习习惯，有了它，学生可以轻松快捷地学好知识。反之，如果养成书写潦草、做题马虎等不良的学习习惯，不仅增加学生学习的负担，而且有损于学生的身体健康。

由此得出，在教学中需要借助转化思想为学生数学学习搭建平台，提高小学生的数学学习能力。

二、转化思想在小学数学教学中的应用

转化思想是从未知领域发展，通过数学元素之间的因果联系向已知领域转化，从中找出它们之间的本质联系，解决问题的一种思想方法。在小学数学中，主要表现为数学知识的某一形式向另一形式转变，即化新为旧、化繁为简、化曲为直等。

1. 化新为旧

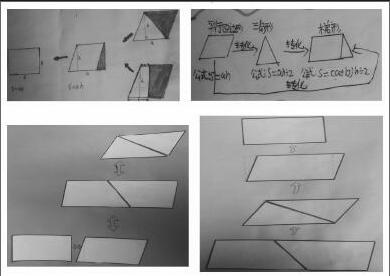
任何一个新知识，总是原有知识发展和转化的结果。在实际教学中，教师可以把学生感到生疏的问题转化成比较熟悉的问题，并利用已有的知识加以解决，促使其快速高效地学习新知，而已有的知识就是这个新知的生长点。如空间与图形中的平行四边形、三角形、梯形等图形的面积公式推导，它们均是在学生认识了这些图形，掌握了长方形面积的计算方法之后安排的，是整个小学阶段平面图形面积计算的一个重点，也是整个小学阶段中能较明显体现转化思想的内容之一。

2. 化繁为简

在处理和解决数学问题时，常常会遇到一些运算或数量关系非常复杂的问题，这时教师不妨转化一下解题策略，化繁为简。反而会收到事半功倍的效果。

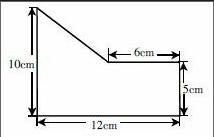
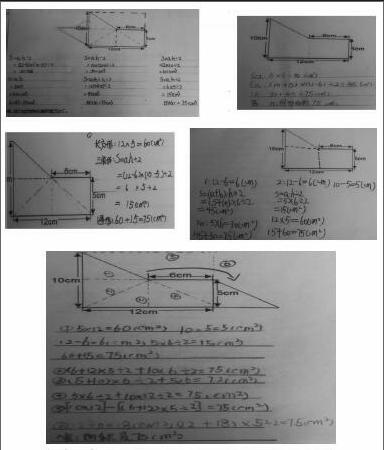
例如，在五年级上学期，新授求组合图形的面积。（如上图）之前学生已经学会并掌握了长方形、正方形、平行四边形和三角形的面积计算方法，在此经验和基础之上，引导学生利用分割或者补全的方法将复杂的组合图形转化为简单的、基本的平面图形，进而计算它们的面积之和。通过小组讨论后，学生的答案可谓精彩纷呈。

3. 化曲为直

“化曲为直”的转化思想是小学数学曲面图形面积学习的主要思想方法。它可以把学生的思维空间引向更宽更广的层次，形成一个开放的思维空间，为学生今后的发展打下坚实的基础。

例如，圆面积的教学，教师在教学过程中，先请学生把圆16等分以后，请他们动手拼成近似的平面图形，即用转化思想，通过“化曲为直”来达到化未知为已知。学生兴趣盎然，通过剪、摆、拼以及多种感官协同参与活动；或把其中的每一份再平均分成两份后，拼成近似的长方形，从而推導出面积公式：s=πR2。当学生得出圆面积公式后，教师又创设一个情境：将圆平均分成32、64、128、256、512、1024……让学生想象，拼出的图形是否越来越接近标准的长方形、平行四边形、三角形和梯形。学生在这种“有限割拼，无限想象”的学习中，初步感受到了“化曲为直”转化思想的教育，同时也体会到了数学的简洁美，激发了学生的学习兴趣，并为今后学习奠定了基础。endprint

三、借助转化思想提高小学生数学学习能力的实践研究

新课标指出：数学课程改革要以反映未来社会公民所必须的数学思想方法为主线，选择和安排教学内容。因为数学的思想与方法是数学的灵魂，学生一旦拥有它，将终身受益。

五年级上学期在学习《三角形的面积》一节新授课时，笔者没有按照以往的旧教法直接告诉学生三角形的面积公式，让学生直接利用公式去计算；而是以学生身边的实际问题“怎样计算红领巾的面积”为载体，以小组合作学习的形式展现学生探索交流的过程，呈现学生操作活动的多样性。在学生探索交流的过程中，引导学生探索三角形的面积可以借助已经学过的平行四边形的面积来推导。因前面学习小数除法和平行四边形的面积时，学生经历了将新知转化为已经学过的知识，将复杂的问题转化为简单的问题，在学生探索的过程中已经渗透了转化的思想，有利于探究新知，所以推导三角形的面积在转化思想的帮助下就显得简单了许多。不仅通过学生小组合作推导出了三角形的面积，而且还经历了三角形的面积为什么要除以2，难点也就不攻自破了。

学生不仅仅复习了每个多边形的面积计算公式以及推导过程，而且还找出了它们之间的联系，并用箭头把它们连起来，把一个一个单一图形的面积连成了一个知识网络，（将平行四边形转化为长方形；三角形和梯形都可以转化为平行四边形；组合图形转化为基本图形）充分地体现了转化思想的重要性和实效性，也用事实证明了学生已经拥有了转化的意识，学习上具备了转化的思想，并通过转化的思想找到了数学的本质，找到了多边形面积的根。

正如著名数学家乔治·波利亚所云：“完善的思想方法犹如北极星，许多人通过它而找到了正确的道路。”在平时教学中，教师要努力挖掘数学知识中所蕴涵的转化思想及其他数学思想，把握运用数学思想解决问题的机会，增强学生主动运用数学思想的意识，以此提高学生的数学能力，提升学生的数学素养，促进学生的全面发展，为学生数学能力的可持续发展奠定基础。

参考文献：

[1] 教育部.数学课程标准（实验稿）[S].北京：北京师范大学出版社，2011.

[2] 路沙·彼得.无穷的玩艺：数学的探索与旅行[M].大连：大连理工大学出版社，2008.

[3] 王本陆.课程与教學论[M].北京：高等教育出版社，2004.

[4] 杨高全.数学教育新论[M].长沙：中南大学出版社，2003.endprint