一种基于概率盒-PSO-SVM的滚动轴承故障诊断方法

, , ,

(1.昆明理工大学 城市学院,昆明 650051; 2.昆明理工大学 信息工程与自动化学院,昆明 650500)

滚动轴承广泛应用于旋转机械,它运行状态的好坏将直接影响整台机器的功能,因此对滚动轴承故障诊断技术的研究具有十分重要的意义[1].信息融合改变了传统的故障诊断各研究点之间无交叉的研究模式,成为一个新的研究热点[2-4].但多数融合方法在融合前都需要对原始信号进行特征提取,这将导致原始信号丰富信息的丢失,并且很难有效地解决多源信息的时空配准问题,多数研究都局限于同类信息.

概率盒(probability box,p-box)理论对原始信号的包容性及其在不确定性问题方面的强大优势,为上述两个问题的解决提供了一种新的研究途径[5].利用p-box建模能将诸多主观和客观的不确定因素考虑进去,弥补了传统特征提取方法丢弃丰富概率统计信息的缺陷,真实反映了系统全面不确定性.将原始信号先转化成p-box,再实现p-box的信息融合,解决了信息融合时空配准困难的问题[5].

支持向量机(support vector machine,SVM)是一种基于统计学习理论和VC维结构风险最小原理的模式识别方法.它能有效地处理小样本、高维及非线性等学习问题[6],广泛应用于故障分类[7].支持向量机在分类时,关键是核函数宽度σ2和惩罚因子C的选择[8].SVM分类时会根据经验选择核函数宽度σ2和惩罚因子C,导致识别率较低[9-11].如果SVM参数的优化中引入粒子群优化(particle swarm optimization,PSO)算法,这一缺点将得到明显改善.

本文应用p-box的不确定性统计方法组成p-box特征向量矩阵来实现p-box的特征提取,获得用于识别的特征向量.以正确识别率为优化目标,应用粒子群算法优化支持向量机两个影响正确识别率的重要参数,提出基于p-box和PSO-SVM的滚动轴承故障诊断方法,并用实验数据验证算法的有效性.

1 概率盒建模及其融合

1.1 概率盒

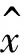
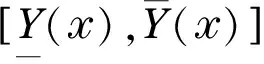
(1)

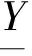
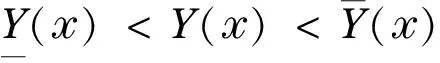
(2)

p-box的核心DSS是由多个焦元组成的集合,DSS表达式为

{([x1,y1],m1),([x2,y2],m2),…,([xn,yn],mn)}

式中,m为基本概率分配,也称为概率片,每个焦元([xi,yi],mi)满足以下条件:

xi≤yi

(3)

∑mi=1

(4)

其中,i=1,2,…,n,如果存在xi=xj,应确保yi≠yj.

由DSS可以绘制出p-box,p-box的左边界可由式(5)累计得到

(5)

p-box的右边界可由式(6)累计得到

(6)

p-box与DSS之间关系如图1所示,粗直线包含的为p-box,两细虚线包含的矩形即是DSS的焦元,横坐标表示区间,矩形的高表示焦元的mass值.p-box正是由多个DSS焦元累计而成.

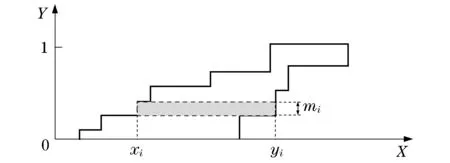
图1 p-box的离散化示例Fig.1 Discretization of p-box

p-box间的卷积运算必须通过DSS来实现.p-box向DSS的转化过程类似于模拟信号的数字化离散过程,如图2所示(见下页).每两细虚线之间为DSS的焦元,这里被离散化为等间距,即每个焦元对应的mass值相等.很显然,离散率越大,越能拟合p-box.

1.2 概率盒建模

如图3所示(见下页)为故障信号p-box建模方法流程图.其建模方法共有3种,分别是已知概率分布类型条件下的p-box建模方法、故障特征p-box建模方法和p-box直接建模方法.本文采用p-box直接建模方法,其具体算法表述如下:将原始数据按采样频率转化为m行n列的数组,其中m为采样次数,n为采样频率,截除多余数据;将每次采样数据按从小到大的次序排列,得到新的数组;从m次采样数据中找到每列中的最小值和最大值,分别得到一个最小值和最大值的行向量;分别累加最小值行向量和最大值行向量得到p-box的下界和上界.p-box直接建模得到的p-box的边界是最窄的,即紧致性最高,且无需验证数据是否服从任何概率分布类型,故采用p-box直接建模方法.

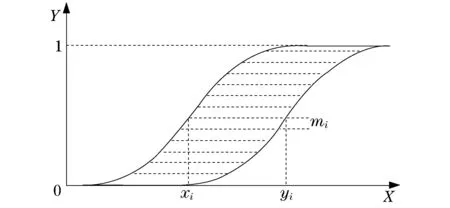
图2 p-box的等概率离散化Fig.2 Equal probability discretization of p-box

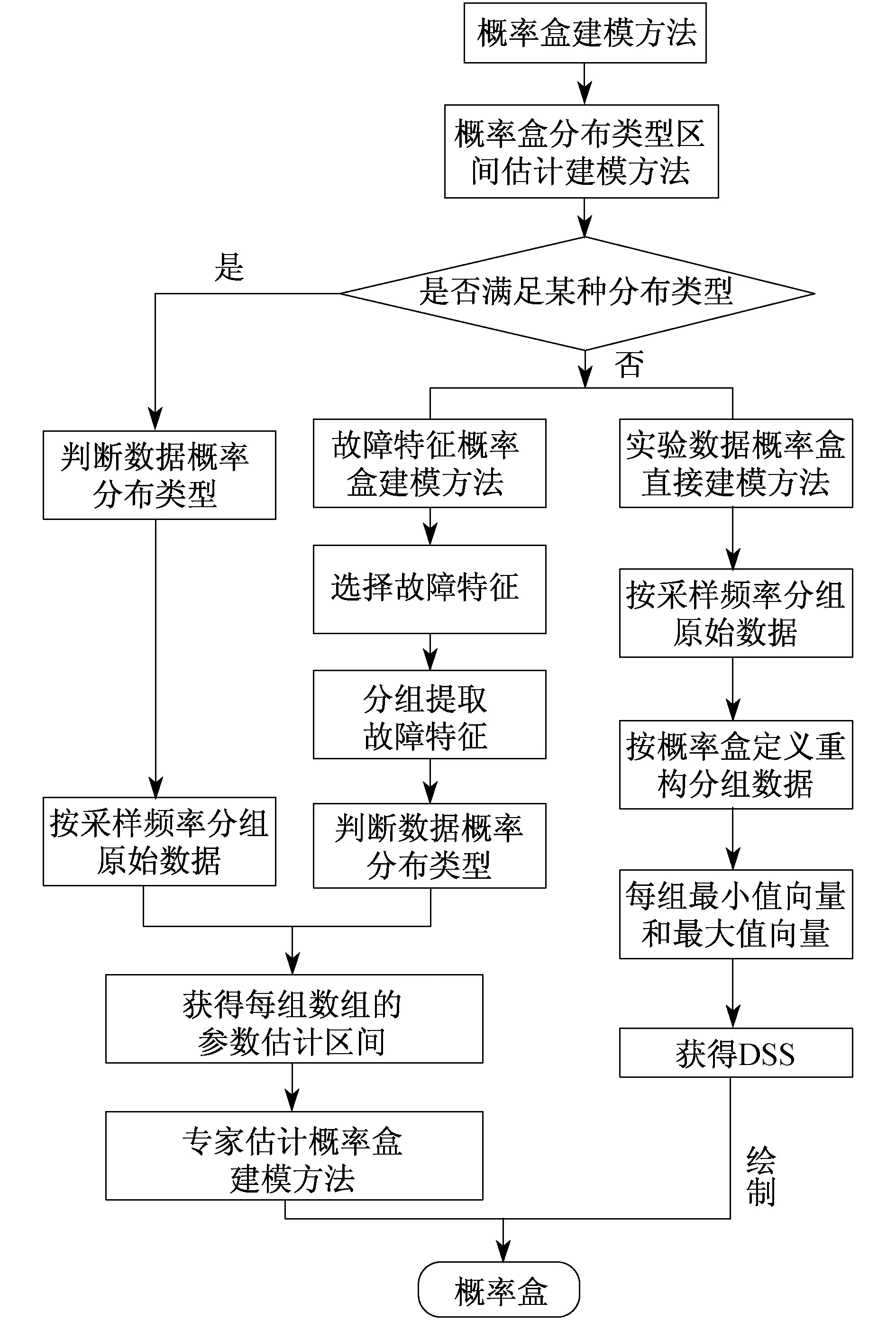
图3 故障信号p-box建模方法流程图Fig.3 Flow chart of the p-box modelingmethod for fault signals

1.3 概率盒的融合

通过概率盒建模方法可以将实验测得的故障信号转化成概率盒,从不同位置获得的故障信号之间存在着信息的冗余,也存在着信息的互补,这就需要对概率盒进行融合.无论采集到的是同类信息还是异类信息,最终都将转化为概率盒,这为异类信息融合提供了一个统一的融合框架.概率盒理论的核心DSS是由证据理论的作者提出来的,DSS和DS证据理论在主要观点上保持了高度的一致性与互补性[5],为此本文采用证据理论来融合概率盒.

采用证据理论融合概率盒的方法为:输入需要融合的概率盒或已离散化了的DSS和需要的离散率或离散点数;设定默认的离散点数,当用户未给出离散点数时,按默认点数计算,否则按用户给出的点数计算;归一化输入的DSS,利用DS证据合成规则,分别对按等离散点数离散后的DSS进行逐对融合,得到新的经过DS证据合成规则融合后的DSS[12-14];对融合后的DSS标准化,分别累加DSS的下边界和上边界绘制出融合后的概率盒.

2 基于p-box的滚动轴承特征提取

累积不确定性测量方法能从不同的角度获得p-box的整体相关信息,表现形式为单个标量或区间,而每个标量或区间都可以理解为p-box的一个特征[5].为此,本文采用累积不确定性测量方法实现p-box的特征提取.以下介绍几种特征提取方法.

方法1获得以基本概率分配为权重的所有焦元区间的累积宽度.

(7)

方法2获得以基本概率分配为权重的所有焦元区间的累积对数宽度.

(8)

方法3获得以基本概率分配为权重的所有焦元区间的以1为基数的累积对数宽度.

(9)

方法4获得p-box下、上界的以基本概率分配为权重的累积区间边界值.

(10)

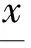
(11)

则p-box的下界和上界的累积边界值公式为

(12)

方法6获得以基本概率分配为权重的p-box之间矛盾区间的统计量.假设p-box的DSS形式为

按式(13)可获得累积不确定性测量结果

(13)

3 基于粒子群优化的支持向量机

PSO算法是基于群体的,根据对环境的适应度将群体中的个体移动到好的区域[15].然而它不对个体使用演化算子,而是将每个个体看作是D维搜索空间中的一个没有体积的微粒(点),在搜索空间中以一定的速度飞行,这个速度根据它本身的飞行经验和同伴的飞行经验来动态调整.假设第i个微粒表示为Xi=(xi1,xi2,…,xiD),它经历过的最好位置(有最好的适应值)记为Pi=(pi1,pi2,…,piD),也称为Pbest.在群体所有微粒经历过的最好位置的索引号用符号g表示,即Pg,也称为gbest.微粒i的速度用Vi=(vi1,vi2,…,viD)表示.对每一代,它的第d维(1≤d≤D)根据如下方程进行变化:

式中:w为惯性权重;c1和c2为加速常数;rand()为在[0,1]范围内变化的随机值.微粒的速度Vi被最大速度Vmax所限制.如果当前对微粒的加速导致它在某维的速度vid超过该维的最大速度vmax,d,则该维的速度被限制为该维的最大速度vmax,d.wvid为微粒先前行为的惯性;c1rand()(pid-xid)为“认知”部分,表示微粒本身的思考;c2rand()·(pgd-xid)为“社会”部分,表示微粒间的信息共享与相互合作[16-18].

首先将粒子初始化.由参数σ2和C组成一个粒子,并随机产生一组粒子的初始位置和速度.确定粒子个数、惯性权重、加速系数、迭代次数.接着进行适应度评估.由于实际的故障类型与分类结果的正确分类率充分反映了SVM的分类精度,因此,将正确分类率作为PSO算法的适应度函数.对每个粒子,将其适应度值与其经历过的最好位置Pbest作比较,如果较好,则将其作为当前的最好位置Pbest.根据式(14)和式(15)更新粒子的速度和位置,检验是否符合结束条件(迭代次数达到了给定的最大次数或达到最小误差要求),如果符合,则停止迭代; 否则转至粒子适应度评估.

4 基于p-box和PSO-SVM的故障诊断

如图4所示为基于p-box和PSO-SVM的故障诊断流程图.在机械故障模拟实验平台上进行不同故障的滚动轴承信号采集,拾取滚动轴承振动信号.

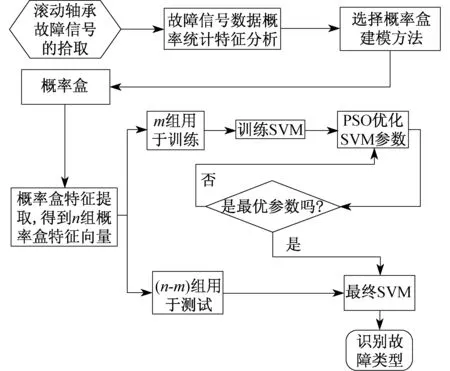
图4 基于p-box和PSO-SVM的故障诊断流程图Fig.4 Flow chart of the fault diagnosis basedon p-box and PSO-SVM

本文对不同的轴承类型使用概率盒建模方法将原始信号先转化成p-box,再实现p-box的信息融合,从而解决信息融合时空配准困难的问题.用p-box特征提取方法对融合后的p-box进行特征提取,获得特征向量.将得到的n组p-box特征向量中的m组用于训练,(n-m)组用于测试,将m组训练特征向量输入到SVM中,通过PSO算法优化训练SVM参数,来减小分类误差,得到训练好的SVM.将(n-m)组测试特征向量输入到训练好的SVM中,训练好的SVM能识别出其所属的状态类别,从而实现不同故障的诊断.

5 滚动轴承故障诊断实例分析

以滚动轴承故障信号为具体研究对象.实验台采用QPZZ-II旋转机械综合故障模拟试验台,信号采集采用美国NI PXI-1042Q高性能声振测试系统,软件采用LabVIEW数据采集软件,传感器采用美国PCB M603C01 ICP加速度传感器,实验装置如图5所示.在轴承座上方(V向)和侧边(H向)分别布置一个ICP传感器,如图6所示.

图5 实验装置实拍图Fig.5 Picture of the experimental apparatus

图6 ICP传感器布置测点Fig.6 ICP sensor arrangement points

实验轴承为NU205圆柱滚子轴承,在外圈和内圈上分别切割出长宽深为15 mm×0.5 mm×0.5 mm的线割槽,用来模拟外圈、内圈局部损伤故障;在其中一个滚动体上切割出宽深为0.5 mm×0.5 mm的线割槽,用来模拟滚动体局部损伤故障,故障轴承实体如图7所示.

电机转速为800 r/min,采样频率为10 240 Hz,由理论公式得到的滚动轴承故障特征频率如表1所示.

图7 故障轴承实体图Fig.7 Pictures of fault bearings

轴承部位内圈外圈滚动体保持架故障特征频率/Hz95．3664．6033．385．38

实验轴承加速度信号的时域波形和功率谱如图8所示.

通过概率盒建模方法获得的结果如图9和图10所示.图中共有4个概率盒,分别对应着正常轴承、内圈故障、外圈故障及滚动体故障轴承概率盒.

对比图9和图10发现,内圈与外圈概率盒在V向存在交叉现象,但在H向无交叉现象;内圈与滚动体概率盒在H向存在交叉现象,但在V向不交叉.这是因为V向布置的传感器位于轴承座的非承载区,经过该区域的滚动体与内圈和外圈之间的径向间隙很接近,滚动体与外圈故障的冲击和滚动体与内圈故障的冲击带来的不确定性很类似,故从V向获得的内圈故障概率盒和外圈故障概率盒很相似,无法完全分离开来,导致了交叉现象的发生.内圈与滚动体在非承载区之间的径向间隙较大,故内圈故障和滚动体故障概率盒在V向可以实现完全分离,即无交叉现象发生.但H向布置的传感器接近轴承座的承载区,滚动体与内圈和外圈之间的径向间隙因为承受载荷的关系而发生较大的变化,故H向得到的内圈故障和外圈故障概率盒很容易实现分离,即无交叉现象的发生.内圈和滚动体进入承载区后,两者之间的径向间隙变小,导致内圈故障概率盒和外圈故障概率盒在H向无法完全分离,即带来了交叉现象.

通过以上分析发现,在不同位置布置的传感器获得的在相同轴承状态下的数据不确定性是存在信息的冗余和互补的,因此需要通过概率盒的融合来优化不同轴承状态下获得的概率盒.采用证据规则融合图9、图10概率盒的结果如图11所示.

分析图11发现,各概率盒间的交叉现象得到了很大改善,这将更有利于下一步的模式识别.

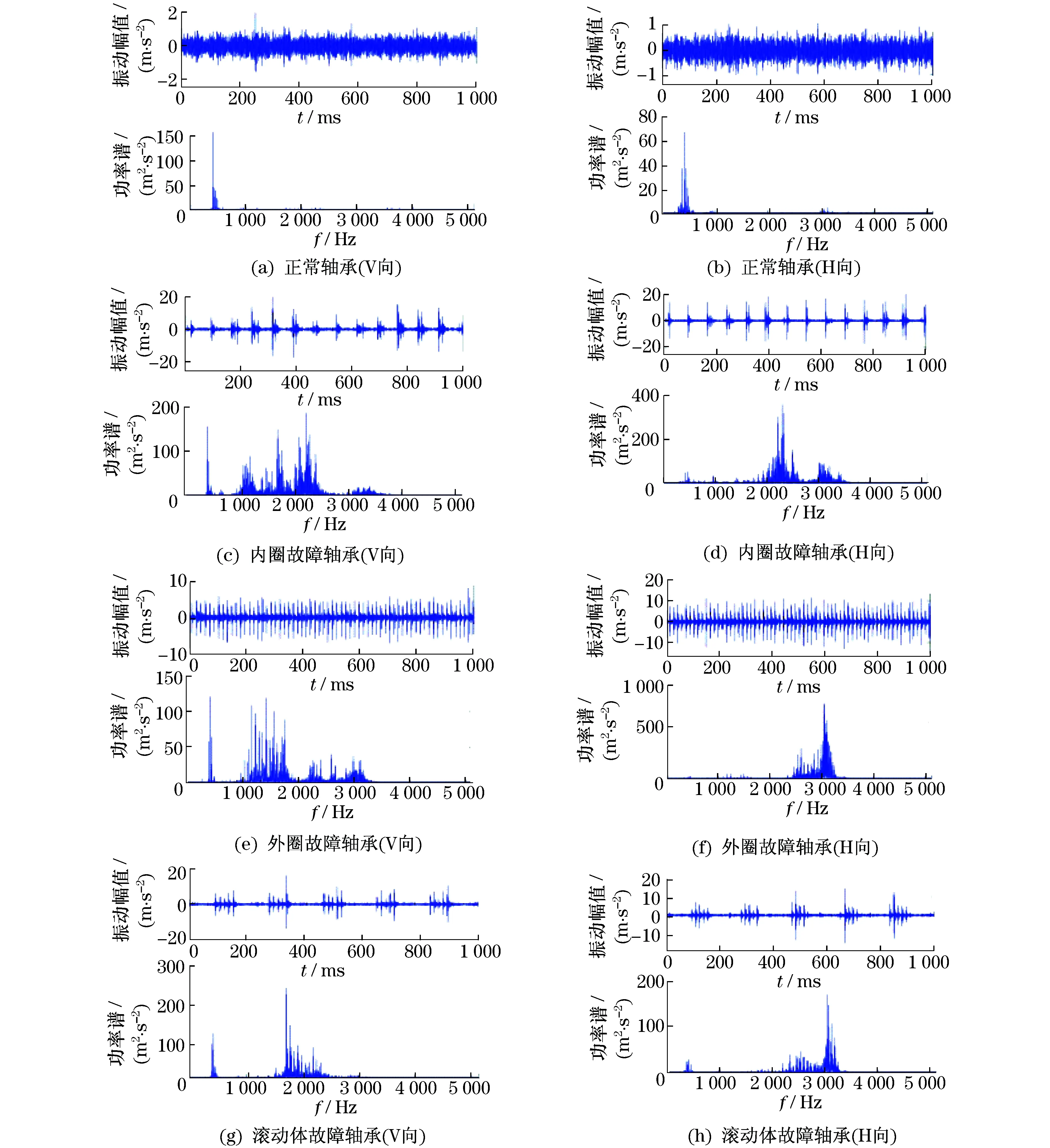
图8 实验轴承加速度信号的时域信号和功率谱Fig.8 Time domain signal and power spectrum of the acceleration signal of the experimental bearing

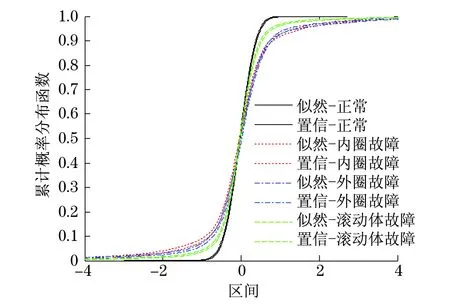
图9 实验结果(V向)Fig.9 Experimental result(V direction)

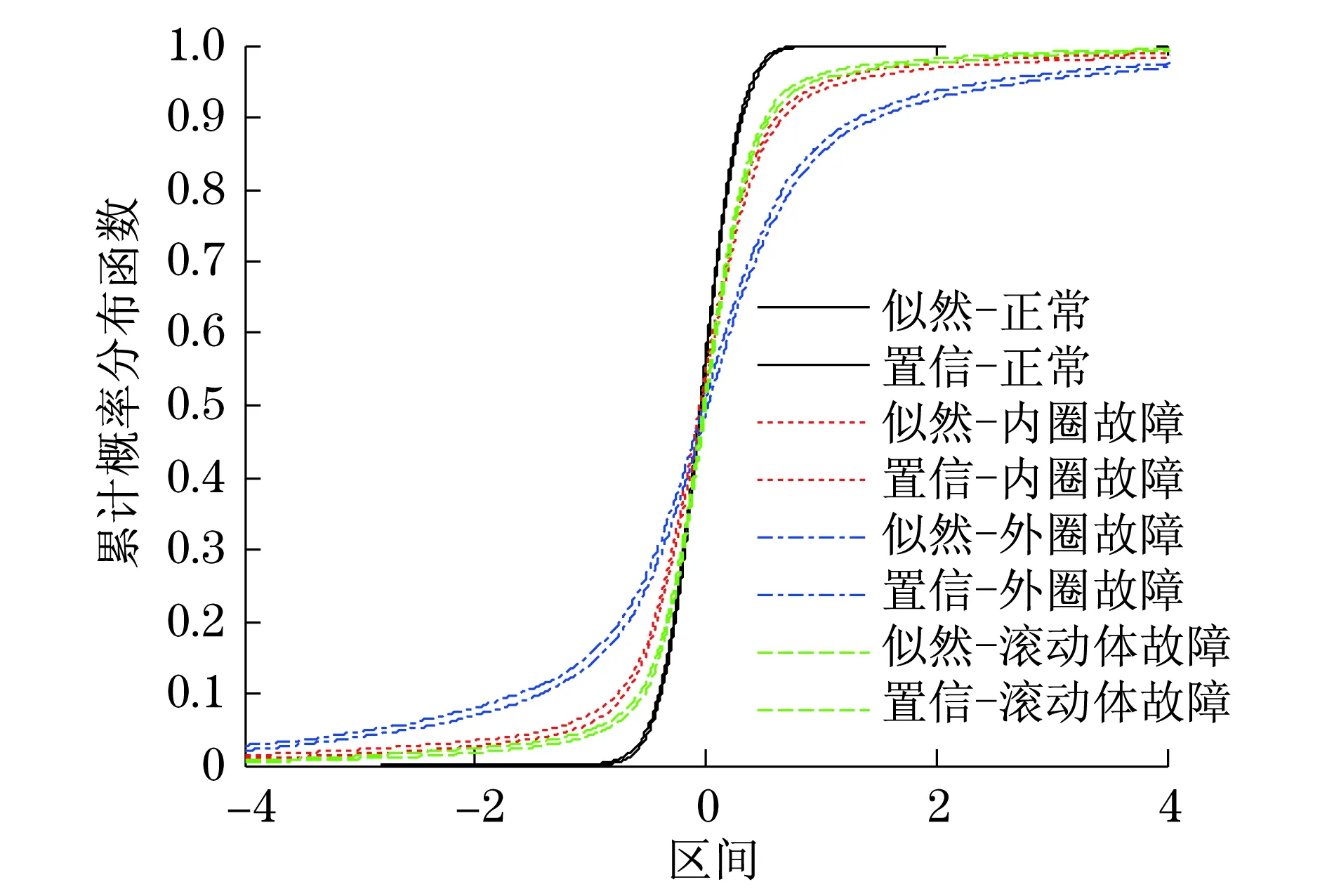
图10 实验结果(H向)Fig.10 Experimental result (H direction)

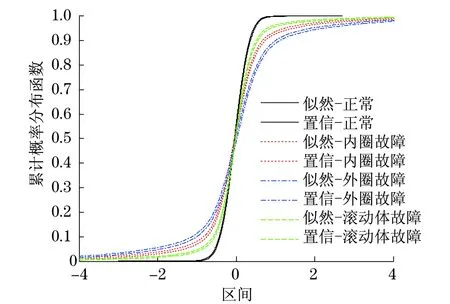
图11 p-box融合结果Fig.11 Fusion results of p-boxes

利用上文提到的概率盒特征提取方法对图11的4个概率盒进行特征提取,结果如表2所示.

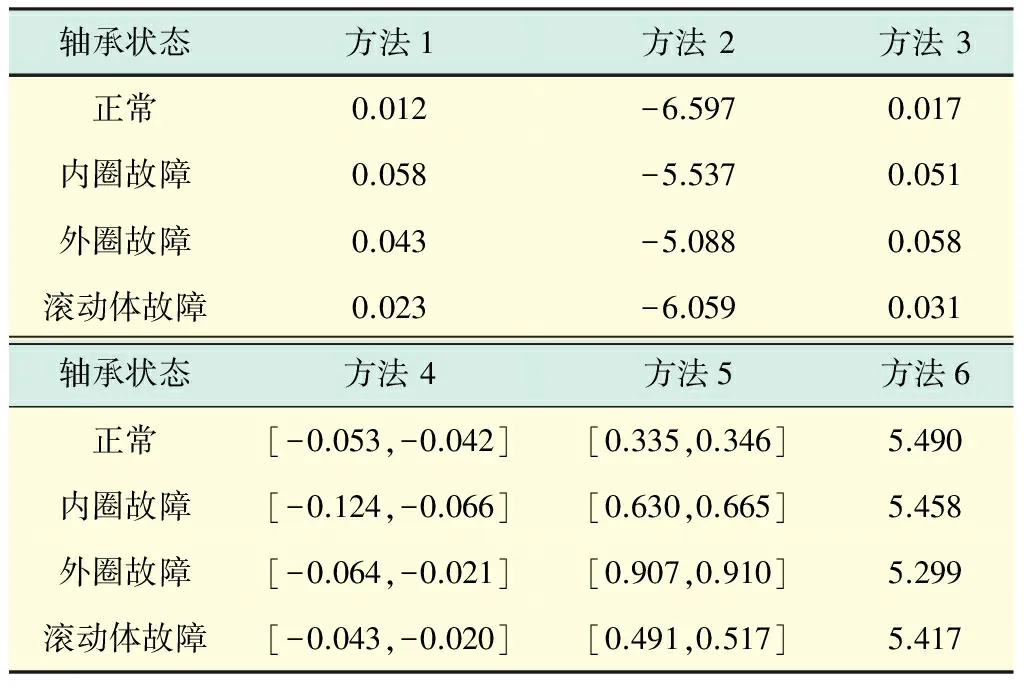
表2 p-box特征向量数据 (fs=10 240 Hz)Tab.2 Data of p-boxes feature vector (fs=10 240 Hz)

根据实验数据,分别获得每类轴承150组概率盒特征向量,100组用于训练,余下50组用于测试,共4类轴承,即总样本数为600组,训练样本集T1占2/3,测试样本集T2占1/3.表3给出的就是其中一组p-box的特征向量,由6种不同的累积不确定性统计方法得到8个特征,组合后构成特征向量.

设定σ2的优化区间为[0.01,500],C的优化区间为[1,2 000],粒子群算法的参数设置如表3所示.

表3 粒子群算法参数设置Tab.3 Parameter settings of PSO algorithm

建立4类轴承状态模式识别的纠错编码.以正确识别率为寻优目标函数,以SVM的核函数宽度σ2和惩罚系数C为优化对象,用PSO优化得到8个SVM的关键参数如表4所示.

表4 PSO算法优化SVM参数结果Tab.4 Optimized results of SVM parameters

利用“汉明距离最小法”对8个SVM分类结果与纠错编码比对,得到的模式识别结果如表5所示.从表5可以看出,基于PSO-SVM的故障识别方法能够完全识别出轴承的正常状态和外圈故障状态,在滚动体故障方面,仅有少量样本被识别错误.

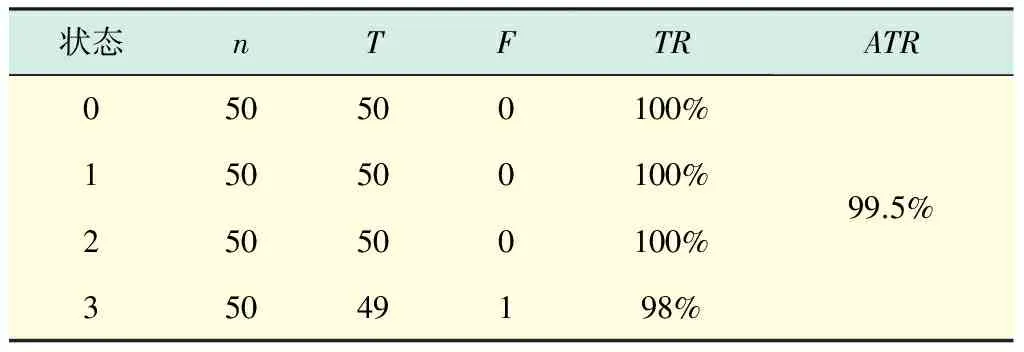
表5 PSO-SVM的测试样本分类结果Tab.5 PSO-SVM test sample classification

注:表中状态列的0,1,2,3分别代表正常、内圈、外圈及滚动体故障;n,T,F,TR,ATR分别代表测试样本数、正确分类数、错误分类数、正确分类率及总正确分类率.

为了进一步说明本文方法与传统方法的差别,以传统的无量纲特征:波形指标、脉冲指标、峰值指标、裕度指标、偏斜度指标、峰态指标、歪度指标和峭度指标为8个特征向量,以SVM为模式识别工具,仍选用600组样本数据,2/3用于测试,剩余1/3用于识别,得到的对比结果如表6所示.结果表明,本文方法的总正确识别率优于传统特征提取方法.

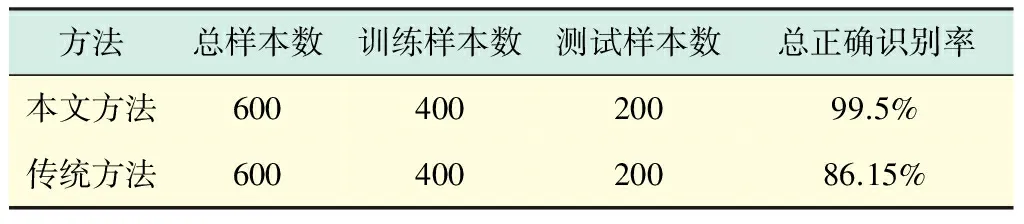
表6 本文方法与传统方法比较结果Tab.6 Comparison of the method proposed with

6 结 论

a. 针对传统滚动轴承的原始数据的特征提取方法的不足,提出基于概率盒的滚动轴承故障建模方法.该方法利用了概率盒对原始信号的包容性及其在不确定性问题方面的强大优势,弥补了传统特征提取方法丢弃丰富概率统计信息的缺陷;采用证据理论的融合规则能更加有效地提升概率盒处理不确定性随机变量的能力;累积不确定性测量方法可以实现概率盒的特征提取,获得用于识别的特征向量,这一特征向量更具稳健性,不易受信息丢失的影响.最后利用PSO-SVM作为分类器实现了故障诊断.

b. 通过实验数据对比了传统特征提取与概率盒建模特征提取对正确识别率的影响,验证了方法的有效性.实验结果表明:采用概率盒直接建模得到的概率盒的边界是最窄的,即紧致性最高;利用概率盒提取的特征向量和PSO对SVM进行优化,使得SVM获得了较高的模式识别率.

[1] 余肖生,田智星,余梅.多源信息融合研究综述[J].重庆理工大学学报(自然科学),2015,29(12):100-104.

[2] 杜奕,丁家满,刘力强.基于概率盒理论的滚动轴承故障信号建模方法[J].振动与冲击,2016,35(19):31-37.

[3] 魏峻.一种有效的支持向量机参数优化算法[J].计算机技术与发展,2015,25(12):97-100.

[4] 程思嘉,张昌宏.基于粒子群算法优化最小二乘支持向量机的电路故障诊断方法[J].兵器装备工程学报,2016,37(3):98-101.

[5] 卢山,徐帷,刘宗明,等.面向高轨航天器的在轨操控技术[J].宇航学报,2014,35(4):425-431.

[6] 梁斌,杜晓东,李成,等.空间机器人非合作航天器在轨服务研究进展[J].机器人,2012,34(2):242-256.

[7] 徐咏梅,柳桂国,柳贺.高斯径向基核函数参数的GA优化方法[J].电力自动化设备,2008,28(6):52-55.

[8] 史岩,李小民,齐晓慧.基于Vague-Sigmoid核函数的PSVM故障诊断算法研究[J].信息技术,2012(3):13-16.

[9] 于雷,吴舜泽,马寅,等.基于二分类Logistic回归模型的COD总量减排措施的绩效分离评估[J].水资源保护,2013,29(6):75-79.

[10] 祖文超,苑津莎,王峰,等.基于SVM的纠错编码多分类算法的研究与应用[J].电子质量,2012(7):38-40.

[11] GERIST S,MAHERI M R.Multi-stage approach for structural damage detection problem using basis pursuit and particle swarm optimization[J].Journal of Sound and Vibration,2016,384:210-226.

[12] 冯冬青,邢广成,费敏锐,等.基于改进PSO算法的多变量PID型神经网络控制[J].系统仿真学报,2011,23(2):363-366.

[13] 方伟,孙俊,谢振平,等.量子粒子群优化算法的收敛性分析及控制参数研究[J].物理学报,2010,59(6):3686-3694.

[14] 刘福才,贾亚飞,任丽娜.基于混沌粒子群优化算法的异结构混沌反同步自抗扰控制[J].物理学报,2013,62(12):120509.

[15] SHAFER G.The combination of evidence[J].International Journal of Intelligent Systems,1986,1(3):155-179.

[16] ZADEH L A.Review of books:a mathematical theory of evidence[J].The AI Magazine,1984,5(3):81-83.

[17] SHAFER G.A mathematical theory of evidence[M] Princeton,NJ:Princeton University Press,1976.

[18] KARLINS,STUDDEN W J.Tchebycheff systems:with applications in analysis and statistics[M].New York:Wiley Interscience Publishers,1966.