基于随机概率密度演化的结构-TMD参数优化
2018-02-03,,,,
, , , ,
(1.云南大学 建筑与规划学院,昆明 650091; 2.广西大学 广西防灾减灾与工程安全重点实验室,南宁 530004)
调频质量阻尼器(TMD)可以通过调整弹簧系数与阻尼系数的大小使吸振阻尼器尽量接近激振频率,从而起到减小建筑结构在风、地震等外部激励下的振动响应的作用,是一种有效、常用的被动控制装置.为此,合理地选择TMD参数显得尤为重要.在实际工程中,地震等随机激励往往成为建筑结构破坏的主因,因此带来的结构-TMD参数的不确定性优化选择成为研究的重点.
近几十年,由于力学、数学以及计算机的进展,确定性激励下的结构优化设计和随机激励下线性优化得到了快速而广泛的发展.但是,随机激励作用下的结构非线性响应约束条件求解困难,成为随机优化设计问题的瓶颈.
在结构全寿命周期内,由于载荷的随机性,结构将不可避免地进入非线性阶段. 然而,为了处理问题的方便,人们常常将随机振动与随机结构人为割裂开来,不考虑两者的耦合效应. 其中,具有代表性的有功率谱分析、矩演化方法与FPK方程(Fokker Planck Kolmogorov equation)等[1-2],而在随机结构分析中具有代表性的方法主要有随机模拟方法、随机摄动技术与正交多项式展开理论等.这些方法主要集中在平稳激励和低自由度情况,而对于多自由度非线性系统,结构非线性与随机性的耦合效应对随机激励下随机结构非线性分析带来了巨大困难,而陈建兵等[3-4]提出的广义概率密度理论,其演化方程的维数与原系统的维数无关,因此,求解多自由度问题更为方便.而且既可以直接获得随机结构响应的概率密度函数,又可以同时考虑结构特性与激励的随机性.
本文通过基于概率密度演化理论的动力可靠度计算方法求解结构的位移可靠度,将随机激励下结构-TMD系统优化设计的位移约束拓展到可靠度层面,准确描述随机激励下结构-TMD系统的约束条件.从而建立了随机激励下多自由度剪切型框架结构-TMD体系的优化模型.并采用遗传算法对TMD结构的质量、阻尼与刚度进行优化设计.实现了概率密度演化方法在随机激励下TMD建筑结构优化设计中的成功应用.
1 结构-TMD系统优化模型
如图1所示,在框架结构顶层安装TMD控制装置的多自由度TMD建筑结构形式[5-7],图1中mi表示结构体系第i层质量,假设主结构受地震激励,则TMD装置运动方程为
(1)


图1 多层剪切模型Fig.1 Multilayer shear model
由于在工程实际中结构的基础尺寸远远小于地震波的波长,而且在每次地震中造成结构破坏的最主要因素是剪切地震波的作用,所以,假设建筑结构为剪切型模型,即各层之间的梁和板的刚度无穷大,不考虑结构层间的梁板转动变形,则主结构的运动方程为
(2)
式中:[M0],[C0],[K0]分别表示主体结构的质量矩阵、阻尼矩阵、刚度矩阵;{X}为主结构的位移列向量;In为单位列向量.
TMD控制装置对主结构的阻尼调制作用及刚度调制作用分别为
综合式(1)和式(2),可列矩阵方程式(3).
(3)

M=diag (Mj(i)),j=1,2,3,…,n,Mj(i)为结构各层质量.
而结构-TMD系统的刚度矩阵
K=
(4)
式中,ki表示第i层刚度.
主结构的阻尼形式采用瑞雷阻尼,针对设置TMD减震控制装置的结构体系,结构-TMD体系的阻尼矩阵
(5)
式中,a0,a1为不依赖于频率的常数,通常采用实测的结构阻尼比来确定,或通过给定的2个振型的阻尼比的值来确定.
采用哈密顿体系和 Wilson-θ法对TMD框架结构进行了随机激励作用下的弹性动力时程分析,由层单元刚度矩阵,利用刚度集成法求得主结构刚度矩阵,叠加TMD系统的刚度,最后求得整体结构的刚度矩阵.质量矩阵采用集中质量法和瑞雷阻尼,采用Wilson-θ时程积分法对框架结构动力方程进行求解.
2 概率密度演化理论
对于一个包含n个自由度的系统,引入随机向量后,将运动方程[8-9]可以改写为

(6)

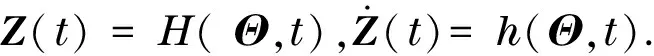
本文选取的物理量是结构层间位移响应,根据概率守恒原理,(Z(t),Θ)所构成的系统概率是恒定不变的,联合概率密度函数pZΘ(z,θ,t)满足广义概率密度演化方程见式(7).广义概率密度演化方程的推导过程详见文献[10].
(7)

式(7)联合概率密度函数pZΘ(z,θ,t)的初始条件可以表示为
pZΘ(z,θ,t0)=pZΘ(z,θ,t)δ(Z-Z0)
(8)
式中:Z0为Z(t)的确定性初始值;δ(·)为Dirac函数.
而对联合概率密度函数进行θ积分,可得到只关于Z(t)的概率密度函数
(9)
式中,Ωθ为θ的分布区域.

通过对概率密度方程的求解,可以很简便地求出在随机作用下的线性与非线性动力反应的概率密度,从而获得二阶及更高阶的统计矩,完整地反映结构体系状态运动规律的随机信息.
3 位移可靠度约束
通常情况下,在结构优化设计中,以结构的最大弹性层间位移限值作为控制指标建立位移极限约束方程.
μj≤μβ,j=1,2,3,…m
(10)
式中:μj为第j层层间位移响应最大值;μβ为给定的结构层间位移限值.
假设结构体系的层间位移响应需满足约束条件μγ≤μj≤μβ,则在t时刻,结构体系层间位移满足约束条件的概率为

(11)
式中,pμj(μj,t)为结构体系在随机激励下第j层层间位移概率密度函数.
在基于首次超越破坏准则的条件下,结构位移响应满足约束条件的概率与结构在t时刻的位移可靠度p(μγ≤μj≤μβ,t)相等,即
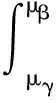
(12)
若要使结构体系在0~t时间段内各个时间点的位移可靠度值不小于pmin,只需要求解出结构体系在激励时间段内所有时间点的位移可靠度,使之满足
p(μγ≤μj≤μβ,0~t)≥pmin
(13)
当采用方程(7)来求解pμj(μj,t)时,参照文献[11],可以对结构施加一个边界吸收壁条件:
(14)
这表明一旦不满足约束条件,则概率进入失效区域,且失效区域内的概率将不再返回有效区域,即该部分的概率被完全吸收,随之可靠度降低.
4 遗传算法
基于随机激励作用下多自由度TMD框架结构非线性响应特点,以位移可靠度为约束条件,采用遗传算法求解TMD的最优质量md,其模型定义为
minf(x),x=x1,x2,…,xn
目标函数f(x)为结构体系的顶层层间位移响应.为了方便遗传算法的应用,将有约束问题转化为无约束问题[12],当第i个个体约束条件满足时,Ci=0;否则,Ci=0.2,该无约束问题为
minφ(x)=f(x)(1+PC)
式中,参数P表示违约对于目标函数的影响,本文P取值为1,表示违约一次,目标函数增大,其代表的个体更容易被淘汰.
在迭代过程中,需要对每一代种群个体的适应度进行评价,其适应度
式中,μi为该种群中第i个个体的适应度.
为了验证本文所选研究方法的严谨性和有效性,以3层钢筋混凝土框架结构减震控制参数的优化设计为例,设基本参数为:第1至第3层质量m=2 762,2 760,2 300 kg,刚度分别为2.485×104,1.921×104,1.522×104 N/m.位移可靠度约束为顶层位移在[-0.05 0.05]m范围内的概率不小于0.9.在基底输入随机载荷,随机载荷采用20条0.2g(g为重力加速度)人工波模拟,采样周期0.02 s.在结构的层间位移响应最小的情况下,得到结构-TMD体系的最优参数.
初设设计变量的取值范围为:md∈(0.03,10.52) t,cd=0.9×c11,kd=0,其中,c11表示结构-TMD体系中阻尼矩阵C内的第一个数.
取筛选概率0.3,交叉概率0.2,变异概率0.2,随机载荷采用20条人工波模拟,种群大小分别取20,30,40,迭代50次,计算结果如表1所示.从表1中可以看出,在最小可靠度pmin=0.9的约束条件下,当TMD质量取4.13 t时,优化后的TMD结构对位移响应的控制效果最优,优化后的最大位移可达到优化前的56.27%.随着种群数的增加,计算结果越来越好,且趋于稳定.图2和图3给出了最优个体顶层的层间位移概率密度演化曲面和典型时刻的概率密度函数曲线.由图2和图3可知,通过对概率密度演化方程进行求解,可以方便地提取任意时刻结构层间位移响应的概率密度信息,这样能够准确地描述结构在任意时刻的随机响应,进而计算出结构在任意时刻的位移可靠度.结果表明,虽然随机激励属于正态分布,但是,位移响应在任意时刻的概率分布既不属于通常假定的正态分布,也不属于其他特殊分布,它具有明显的多峰特性,且随着时间改变而变化.图4给出了优化过程中所有个体的结构顶层层间位移可靠度的平均值变化,由于是在一定的位移可靠度约束下,且目标函数是结构顶层层间位移响应最小,所以,位移可靠度随时间的增加逐渐增加,最终达到位移可靠度约束0.9,表明优化后位移可靠度增加,TMD具有减震效果.
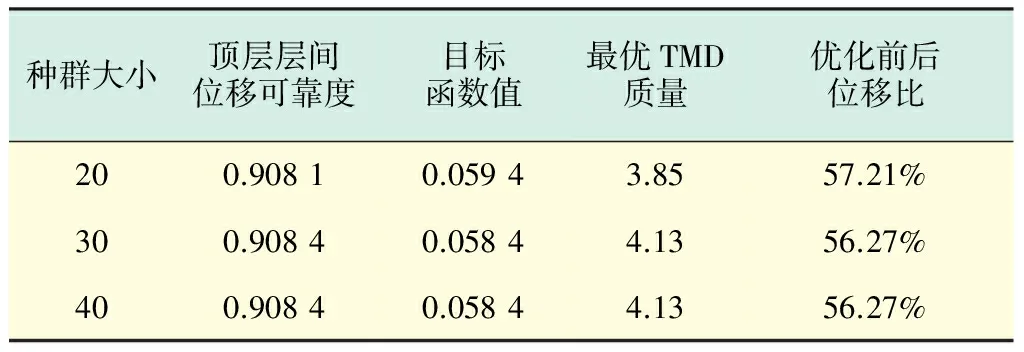
表1 结构优化结果Tab.1 Structural optimization results
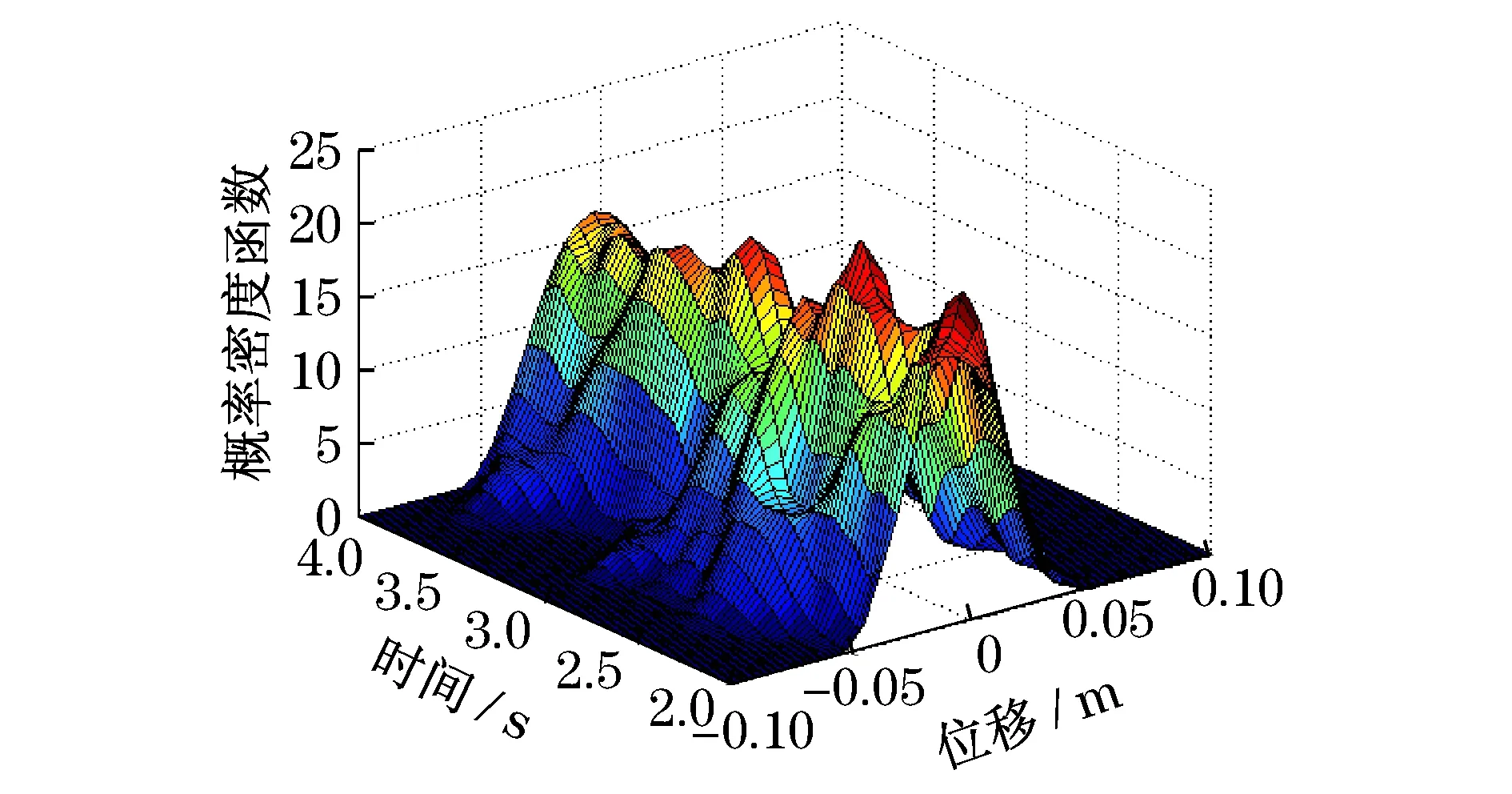
图2 顶层的层间位移概率密度演化曲面Fig.2 Evolving surface of the displacement probabilitydensity function of the top floor

图3 典型时刻的概率密度函数Fig.3 Probability density function at typical time
通过对比优化前后结构顶层层间的位移响应,如图5所示,可以发现:当结构本身位移响应越大的时候,控制效果越明显;当结构本身位移响应很小的时候,TMD装置对结构位移响应的控制效果不明显.所以,总体上TMD对降低结构响应具有很好的效果,优化后的峰值响应为优化前的56.27%.

图4 顶层的层间位移可靠度Fig.4 Vertical displacement reliability of the top floor

图5 优化前后结构顶层层间位移响应Fig.5 Comparison between the displacement responsesat the top and bottom of the structure beforeand after optimization
5 结 论
针对多自由度TMD结构体系在非平稳随机地震作用下的最优TMD参数求解问题,将改进遗传算法中的位移约束条件用随机概率密度理论求解出的位移可靠度描述,解决了传统的位移约束条件对于随机激励下的结构响应的不适应性问题.通过算例可以看出:
a. TMD能够很好地发挥作用,特别是能够降低结构响应的最大峰值,优化后的峰值响应为优化前的56.27%,即大大降低了结构的失效概率.
b. 通过对任意时刻结构位移的概率密度信息进行提取,实现了结构全灾变的准确描述.结果表明,虽然随机激励属于正态分布,但是,位移响应具有多峰的性质,且随着时间的变化而变化,因此,对全过程的概率描述是必要的.
c. 在位移可靠度约束下,对优化过程中所有个体结构顶层层间位移可靠度平均值监测结果说明位移可靠度随时间的增加逐渐增加,最终达到位移可靠度约束0.9的理想效果,进一步说明该方法得到的TMD参数具有良好的减震效果.
本文所提出的思路与方法为计算随机激励下的结构-TMD系统可靠度提供了新的途径,实现了概率密度演化方法在随机激励下TMD建筑结构优化设计中的成功应用,为随机载荷下多塔结构控制优化设计提供了很好的技术支持.
[1] FANG T,WANG Z N.Complex modal analysis of random vibrations[J].AIAA Journal,1986,24(2):342-344.
[2] LUTES L D,SARKANI S.Random vibrations:analysis of structural and mechanical systems[M].Amsterdam:Elsevier,2004.
[3] 陈建兵,李杰.非线性随机地震响应的概率密度演化分析[J].武汉理工大学学报,2010,32(9):6-10.
[4] 陈建兵,张圣涵.非均布随机参数结果非线性响应的概率密度演化[J].力学学报,2014,46(1):136-144.
[5] 谭平,卜国雄,刘红军,等.带TMD结构的随机地震响应分析的新方法[J].北京理工大学学报,2010,30(4):390-394.
[6] 卜国雄.高耸结构基于性能的TMD/AMD设计及其动力可靠度分析[D].哈尔滨:哈尔滨工业大学,2010.
[7] 王磊,谭平,赵卿卿,等.随机结构-TMD优化设计与概率密度演化研究[J].振动工程学报,2015(2):285-290.
[8] 陈建兵,刘章军,李杰.非线性随机动力系统的概率密度演化分析[J].计算力学学报,2009,26(3):312-317.
[9] 李涛,张洵安.基于概率密度演化方法的随机MSCSS构造研究[J].应用力学学报,2011,28(6):576-582.
[10] 陈建兵,李杰.结构随机响应概率密度演化分析的数论选点法[J].力学学报,2006,38(1):134-140.
[11] 陈建兵,李杰.非线性随机结构动力可靠度的密度演化方法[J].力学学报,2004,36(2):196-201.
[12] 唐文艳.结构优化中的遗传算法研究和应用[D].大连:大连理工大学,2002.
