基于三次指数平滑法的沪牌拍卖月均价预测
2018-02-03,
,
(上海理工大学 管理学院,上海 200093)
随着人们生活水平的提高,私家车越来越普及,同时国家对私家车排照的管理也越为严格.对于北京、上海等实施拍牌政策的地区,私家车牌照更是千金难求,多年来车牌竞拍都是社会关注的热点问题之一.随着城市车辆的增多,我国更多地区开始限牌,或将引进汽车牌照拍卖政策.目前,关于车牌拍卖价格预测模型的研究较少,其中,臧其事[1]运用神经网络模型预测上海车牌价格,预测结果误差在10%以内,并得到上海车牌价格从长期来看呈现上涨趋势这一结论.因此,对牌照拍卖价格预测的研究具有较高的现实意义.
本文通过相关性分析发现历史数据适用于短期价格预测,随后主要应用三次指数平滑法及动态三次指数平滑法对沪牌拍卖月均价进行了预测.另外,对这两种方法的MSE和相对误差进行了比较分析,发现动态三次指数平滑法预测结果更优,且较为稳定.
1 指标相关性及研究方法
与拍牌月成交均价直接相关的影响因素有车牌投放数量、投标人数以及历史数据.对2015年和2016年的数据进行相关性分析,结果如表1~3所示,其中前1月到前10月表示以各月为基准的前10个月的历史平均成交价.

表1 2015年投放数量、投标人数、历史数据与月平均成交价相关性Tab.1 Correlation between the influencing factors and the average price in 2015

表2 2016年投放数量、投标人数、历史数据与月平均成交价相关性Tab.2 Correlation between the influencing factors and the average price in 2016

表3 2015-2016年投放数量、投标人数、历史数据与月平均成交价相关性Tab.3 Correlation between the influencing factors and the average price in 2015-2016
由表3可以发现,从长期来看,投放数量、投标人数、历史数据都与月平均成交价在0.01水平上显著相关.由表1和表2可以发现,投放数量在2016年与月平均成交价在0.01水平上显著相关,而在2015年不相关;投标人数在2015年与月平均成交价在0.01水平上显著相关,而在2016年不相关.这说明投放数量、投标人数不适用于车牌月平均成交价的短期预测.同时,表1~2中历史数据与月均价的相关性有所波动,但仍表现出显著相关性.此外,从长期来看,车牌拍卖价格虽然受经济、政策、文化等各方面因素的影响,但在短期内这些外部环境变化不大,利用近期的历史数据对月均价作出预测具有较高的参考价值.本文选取三次指数平滑法作为预测模型.
指数平滑法[2-8]由布朗提出,是在历史数据的基础上,利用指数加权法进行预测的一种方法,已被广泛运用于预测模型中.其中,三次指数平滑法常用于预测具有一定趋势的非线性时间序列.对上海车牌成交月均价进行分析,发现其具有明显的非线性增长趋势,故该模型适用于车牌成交月均价的短期预测.三次指数平滑法理论简单、操作方便、预测效果好,是常用的预测方法之一.Taylor等[9]为了对短期电力需求作出预测,提出了一种新的双季季节性三次指数平滑,这种预测模型能较好地保留电力需求的双季节特征.Burkom 等[10]分别利用3种时间序列预测方法,即非自适应回归模型、自适应回归模型以及三次指数平滑法,对生物监测进行预测,比较3种方法在16种真实数据流中预测的准确性,结果显示三次指数平滑法的预测优于其他两种.Tratar 等[11]利用多元回归和三次指数平滑法,分别以每月、每周和每日为基准,对短期和长期热负荷进行预测,结果显示多元回归法对每日和每周的短期预测效果较好,而三次指数平滑对长期和每月短期预测效果较好.Chen等[8]将三次指数平滑用于单频GPS接收机电子总含量计算的误差预测,依据前六天的计算误差值来预测第七天的误差,从而改进电子总含量的计算方法.传统的指数平滑法中平滑因子固定,而动态指数平滑法[12-15]拥有动态的平滑因子,能更好地适应时间序列的变化趋势.
2 传统三次指数平滑法
一次指数平滑法常用来预测趋势不明显的时间序列,二次指数平滑能较好地预测有明显趋势且为线性的时间序列,三次指数平滑法是对二次指数平滑再进行一次平滑,常常用于对有明显趋势且呈非线性的时间序列进行预测.其基本模型如以下所示.
a. 历史数据平滑.
(1)
式中:α为平滑因子;t为时间序号;Xt为历史数据;St(1)为一次指数平滑值;St(2)为二次指数平滑值;St(3)为三次指数平滑值.
b. 预测.
(2)

at=3St(1)-3St(2)+St(3)
(3)
(10-8α)St(2)+(4-3α)St(3)]
(4)
(5)
c. 预测精度评价.
此处采用均方误差(MSE)对该方法的预测精度进行评价,以选出最优的平滑因子α,当MSE最小时,α最优.其中
(6)
3 动态三次指数平滑法
动态三次指数平滑法由传统的三次指数平滑法改进而来,其平滑因子在不同次的预测中不同,每次预测时平滑因子都会依据现有历史数据进行自我调整,从而达到更好的预测效果.在动态三次指数平滑法中,αk表示第k次预测时的动态平滑因子,并令
(7)
则其基本模型如以下所示.
a. 历史数据平滑.
(8)
b. 预测.
k=1,2,3,…
(9)
其中,
c. 预测精度评价.
k=1,2,3,…
(13)
4 应用实例——沪牌拍卖月均价预测
图1(见下页)为2014—2016年沪牌成交月均价,可以看出该数据集呈明显的非线性增长趋势,且后半部分出现一定程度的周期性,故而适合使用三次指数平滑法来做预测.本文分别利用传统三次指数平滑法和动态三次指数平滑法对沪牌拍卖月均价进行预测,表4为2016年各月沪牌平均成交价格(数据来源于国拍网),本文以1~10月的数据为历史数据,对11月和12月的平均成交价进行预测.
4.1 传统三次指数平滑法预测

图1 2014-2016年各月沪牌平均成交价格Fig.1 Shanghai license plate monthly averageprices in 2014 to 2016
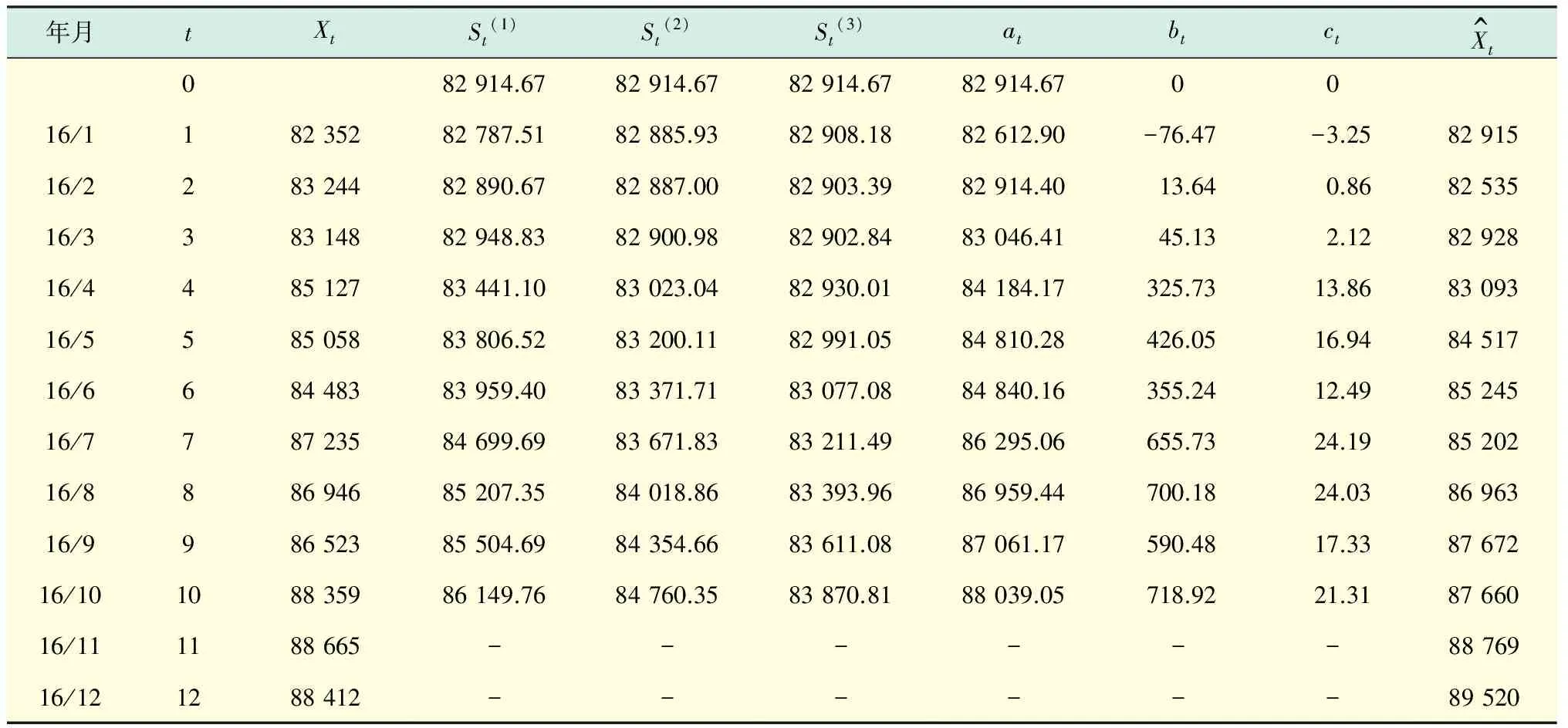
表5 三次指数平滑法预测结果Tab.5 Predicted results based on the three exponential smoothing method

表6 相对误差Tab.6 Relative error
4.2 动态三次指数平滑法预测
此处利用Matlab实现对沪牌2016年11月和12月拍卖成交月均价动态三次指数平滑的预测,利用定步长的梯度下降法使预测的均方误差最小,具体步骤为:
a. 确定初值α0k、步长λ和ε,其中ε>0且为一极小量;
b. 对式(13)求梯度得MSE,将α0k代入MSE,判断‖MSE‖<ε是否成立,若成立,则得到最优值执行步骤d,若不成立,取α0k=αk,执行步骤c;
c. 取αk=αk-λMSE,且有αk>0,将αk代入MSE,判断‖MSE‖<ε是否成立,若成立,则得到最优值执行步骤d,若不成立,继续执行本步骤;

e. 舍去第k次预测中t=1的历史数据,取t=2到t=10的历史数据及t=11的预测值,更新t值,同第k次预测步骤,进行第k+1次预测.
依据上述步骤进行预测,初值α0k取值对预测结果无影响,此处取α0k=0.9,此外取λ=0.000 1,ε=0.01.预测结果及MSE如表7所示,相对误差见表8.2016年11月预测成交月均价为88 158元,12月为88 819元.
比较传统三次指数平滑法与动态三次指数平滑法预测结果的MSE值,可以发现动态三次指数平滑法明显优于传统三次指数平滑法,且对于动态三次指数平滑法来说,预测次数k越小预测结果越优.比较两种方法预测值的相对误差,可以发现传统三次指数平滑法相对误差波动较大,而动态三次指数平滑法较为稳定且相对误差均小于0.6%.

表7 动态三次指数平滑法预测结果Tab.7 Predicted results based on the dynamic three exponential smoothing method

表8 相对误差Tab.8 Relative error
5 结论及展望
本文分别应用三次指数平滑法和动态三次指数平滑法,利用历史数据预测了2016年11月和12月沪牌拍卖成交月均价.比较两种预测方法的MSE,对于动态三次指数平滑法,无论k=1还是k=2,其MSE均小于三次指数平滑法的MSE;比较两种预测方法的相对误差,发现三次指数平滑法对11月预测的相对误差很小,但是对12月预测的相对误差较大,而动态三次指数平滑法对11月和12月预测的相对误差均在0.5%左右.由此可以得出,在沪牌拍卖月均价预测的应用中,动态三次指数平滑法预测结果更优,且较为稳定.本文应用的预测方法准确率较高,可以直接用于实际的车牌月均价预测,预测结果可作为参考为车牌拍卖出价提供帮助,具有一定的实用价值.
虽然本文预测方法简便可行,但影响车牌价格的因素多种多样,直接影响因素有车牌投放数量、投标人数等,间接影响因素有地方政策、社会观念、出行方式的偏好等.因此,利用多影响因素的数据来预测车牌价格是进一步研究的方向.由相关性研究可以看出,从长期来看车牌投放数量、投标人数对车牌价格同样有着重要影响,因此,建立这样一个长期多影响因素的预测模型将是下一步的研究工作.
[1] 臧其事.基于神经网络的上海车牌价格预测模型[J].科技情报开发与经济,2008,18(2):94-96.
[2] 芮海田,吴群琪,袁华智,等.基于指数平滑法和马尔科夫模型的公路客运量预测方法[J].交通运输工程学报,2013,13(4):87-93.
[3] 尹光志,张卫中,张东明,等.基于指数平滑法与回归分析相结合的滑坡预测[J].岩土力学,2007,28(8):1725-1728.
[4] 齐驰,侯忠生.自适应单指数平滑法在短期交通流预测中的应用[J].控制理论与应用,2012,29(4):465-469.
[5] 杨建南,李萍,李世云,等.温特斯线性和季节性指数平滑法预测模型在医院管理中的应用探讨[J].中国卫生信息管理杂志,2010,7(6):74-77.
[6] 赵志伟,杨景明,呼子宇,等.基于一次指数平滑法的自适应差分进化算法[J].控制与决策,2016,31(5):790-796.
[7] 陈武,张山江,侯春华,等.二次指数平滑预测模型回归系数计算方法探讨[J].统计与决策,2016(19):11-12.
[8] CHEN J,HUANG L K,LIU L L,et al.Applicability analysis of VTEC derived from the sophisticated Klobuchar model in China[J].International Journal of Geo-Information,2017,6(3):75.
[9] TAYLOR J W.Short-term electricity demand forecasting using double seasonal exponential smoothing[J].Journal of the Operational Research Society,2003,54(8):799-805.
[10] BURKOM H S,MURPHY S P,SHMUELI G.Automated time series forecasting for biosurveillance[J].Statistics in Medicine,2007,26(22):4202-4218.
[12] 吴德会.动态指数平滑预测方法及其应用[J].系统管理学报,2008,17(2):151-155.
[13] 段功豪,牛瑞卿,赵艳南,等.基于动态指数平滑模型的降雨诱发型滑坡预测[J].武汉大学学报(信息科学版),2016,41(7):958-962.
[14] 孟利民,徐杨.基于动态指数平滑预测的负载均衡算法[J].浙江工业大学学报,2016,44(4):379-382.
[15] 王国权,王森,刘华勇,等.基于自适应的动态三次指数平滑法的风电场风速预测[J].电力系统保护与控制,2014,42(15):117-122.
