气泡在含障碍物微通道内的特性研究

, ,

(上海理工大学 能源与动力工程学院,上海 200093)

气泡运动作为气液两相流系统中一种典型运动,广泛存在于DNA解链[1]、燃料电池[2-3]、微流体机械[4]等领域.近年来,已有很多学者研究了气泡运动现象.Maxworthyt 等[5]用实验方法研究了多个气泡在不同液体中的相互作用及变形现象.Uchiyama等[6]通过实验方法研究了气泡群绕竖直通道中心圆柱上升的运动状况,得到了速度场和绕圆柱障碍物的运动形状.董伟等[7]研究了电场强化沸腾换热中,气泡在不同场作用下运动情况,并定量分析了气泡脱离壁面时的形态.

通过实验研究,可以得到较为明显的宏观参数和宏观现象,但对于细节的现象和问题不能具体描述.一些学者应用微观的数值模拟方法研究气泡上升的运动情况. van Baten 等[8]通过CFD模拟Taylor气泡在循环微管中的上升,主要研究了其中质量传递的情况. Guo等[9]采用改进的两相流PBM模型,研究了受浮力驱动的气泡合并或破裂的情况.微观的研究方法虽然能够得到气泡运动的细节,但存在计算量大的问题,而且关于气泡受浮力驱动在复杂通道内上升的研究仍有不足.

近年来,格子Boltzmann方法逐渐被学者们应用并发展起来.该方法既具有宏观方法能直接研究宏观物体本质的特点,也具备微观方法能研究微小部分具体流动细节的优点.Cheng等[10]基于格子Boltzmann自由能模型和Cahn-Hilliard方程,研究了多气泡在竖直管道内受浮力上升的三维问题.该研究发现:两个相同气泡在一起上升的过程中,放置在上的气泡在气泡合并前保持孤立的状态;而放置在下的气泡同时受到浮力和上个气泡作用产生变形,最终两个气泡合并一同上升.在气泡尺寸有差别的情况下,无论初始条件如何设置,大气泡均在运动过程中占据主导作用.Li等[11]研究了单个气泡绕圆形障碍物上升的问题,发现气泡在穿过障碍时,由于表面张力作用气泡有较大的形变,Eövös数的增加会加大气泡略过障碍后的接触角.本文采用格子Boltzmann方法研究气泡在含障碍物微通道内的动力学特性,分析了障碍壁面润湿度对气泡在竖直通道内受浮力上升的影响.

1 研究方法

1.1 格子Boltzmann模型

本文采用He等[12]提出的改进后的格子Boltzmann模型,该模型的具体内容已在文献[12]有了详细的介绍,本文只作简要描述.

非理想流体的单松弛BGK模型[13]的 Boltzmann方程为

式中:f代表空间内单个粒子的密度分布函数;t为当前时间步长;ξ为微观速度;为哈密顿算子;feq为平衡态分布函数,是宏观物理量(速度矢量u和密度ρ)的函数;λ为松弛时间为模型常数;G为重力矢量;F为分子间作用力矢量,可表示为

F=-ψ+FS

式中:矢量FS=κρ2ρ;κ为表面张力的强度指数;ψ为压力p的函数,表示为

ψ(ρ)=p-ρRT

其中p使用的状态方程为Carnahan-Starling方程,具体表达式为

式中,参数a和b代表气液两相相互作用强度.

9个方向的离散速度分别为

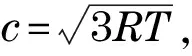
式中:δt为时间步长;φ为索引量;τ为松弛时间,与流体粘性的关系为

演化方程中其他函数定义如下:

宏观量统计由下面方程给出:

式中:φh和φl为索引函数的最大值和最小值,ρl和ρg分别为液相密度和气相密度.φh和φl可由状态方程Maxwell重构得到,本文状态方程中分别取a=4,b=4,其对应的索引函数最大值和最小值分别为0.250 291和0.022 838.

1.2 润湿性处理

本文需要考虑障碍物及壁面的润湿性,润湿性边界条件采用Davies等提出的方法[14],在该方法中采用表面亲和性αs刻画壁面的润湿强度,并把表面亲和性与索引量φ联系起来,其关系式为

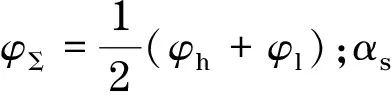
2 模型验证

本文采用Laplace定律来验证模型的正确性.初始时在Nx×Ny区域中心内放置半径为r、密度为ρl的静止圆形液滴,其余区域充满着密度为ρg的气体.当系统达到稳定时,液滴会保持与初始状态基本一致的圆形状态.根据Laplace定律可知,表面张力(σ)恒定,液滴内外的压力差(ΔP)与半径的倒数1/R呈线性关系,关系式如下:

本文模拟不同液滴半径下,Laplace定律的验证情况,半径的变化分别为28,30,32,34,36.在所有模型验证中,网格数为128×128,所有边界条件皆为周期性边界条件.图1给出了数值模拟得到液滴内外压力差pi-p0和1/R之间的关系以及数据拟合结果的对比.从图中可以发现,数值模拟结果与理论结果一致.

图1 液滴内外压力差和半径倒数之间的关系Fig.1 Simulated pressure jump across the dropletinterface versus the inverse of droplet radii

3 模拟结果与分析

数值研究的物理问题如图2所示,其中深蓝色半圆区域代表半径为R1的固体障碍物,因其实际宏观参数不变化,故不参与计算.中下方浅蓝色圆形区域代表半径为R2、密度为ρg的气泡,其初始放置位置为整体高度的1/4处.其余黄色区域充满着密度为ρl的液体.上下边界采用周期性边界条件,左右边界以及固体障碍物表面采用无滑移边界条件.

图2 微通道结构Fig.2 Microchannel structure

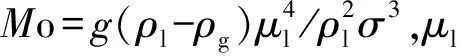
不同的接触角对应不同的润湿性,其中接触角小于90°表示障碍物表面亲水,接触角大于90°表示障碍物表面亲气,接触角等于90°表现为中性.模拟中分别采用30°,60°,90°,120°,150°这5种接触角.模拟网格数为160×480,气泡的半径取值32个格子单位,密度取值0.1,液体密度取值0.5.

3.1 障碍物表面亲水性对气泡运动影响

障碍物表面的润湿性在气泡运动中有重大的影响,本小节主要研究障碍物表面亲水时气泡在上升过程中的影响.

图3给出了障碍物表面接触角为30°时的气泡上升图.由图3可知初始圆形的气泡受浮力作用上升,气泡开始产生形变,逐渐在下半部分产生凹型.在上升经过障碍物时,受到障碍物挤压的作用,气泡开始产生二次形变,并且因障碍物表面为亲水表面,气泡与障碍物之间有明显的间隔,大概3～4个网格.在气泡逐渐挤过障碍时,由于表面张力的存在,气泡整体不会产生破裂现象,但形状变化明显.原本下部分的凹形逐渐变为下部分有弧度的三角形,在经过中间障碍最狭窄的区域时,气泡会受到挤压作用变成“葫芦形”,在缓慢挤出障碍后在表面张力和浮力共同作用下,气泡恢复成球冠形,且下部分弧度比气泡进入障碍时要大.

图4给出了障碍物表面接触角为60°时的气泡上升图.由图可以看出,障碍物表面接触角为60°时,气泡初始的形状与接触角30°时情况类似.气泡在经过障碍物时也会产生二次形变,上升过程虽也与障碍物有明显的距离,但相对接触角30°时,与障碍物的距离更近,更贴近障碍物,整体的形状随障碍物形状变形更加明显.在经过障碍物最狭窄区域时,也会产生“葫芦形”,但“葫芦”的上半部分更大.在整体挤过障碍后,气泡会在下部分出现两个“小触角”,这是由于浮力与障碍物的挤压力共同作用造成的.与接触角30°不同的是,润湿性的不同造成气泡在紧贴壁面的距离不同,在快要挤出障碍物时,60°接触角的气泡下端与障碍物上半部分距离更近,浮力的作用使气泡下部分开始产生弧形的形变,从而产生两个“小触角”.

图3 接触角为30°时气泡的运动过程Fig.3 Bubble rising process with the contact angle of 30 °

图4 接触角为60°时气泡的运动过程Fig.4 Bubble rising process with the contact angle of 60 °

3.2 障碍物表面中性对气泡运动影响

图5给出了接触角为90°(中性)时气泡的动力学过程,从图中可以看出,当障碍物表面润湿性为中性时,在气泡未到达障碍物时,气泡上升的整体过程与亲水情况类似.然而,一旦气泡靠近障碍物,会紧贴着半圆形障碍上升,并在气泡下部分出现两个左右对称的气泡孔.随着气泡不断上升,受浮力作用,气泡下半部分的弧度越来越大.当整体基本挤过障碍物后,气泡的变形更加明显,在浮力作用下,气泡与障碍物表面接触的下部分和整体的气泡脱离并破裂.主要部分继续受浮力作用上升,并受表面张力保持球冠形,小部分留在障碍物的上半圆中,并逐渐向左右两个壁面移动.

图5 接触角为90°时气泡的运动过程Fig.5 Bubble rising process with the contact angle of 90 °

3.3 障碍物表面亲气性对气泡运动影响

为了研究亲气障碍物对气泡动力学行为的影响,图6给出了障碍物表面接触角为120°时气泡的上升过程.从图中可以看出,由于此时障碍物完全亲气,在未接触障碍物前,气泡整体的运动状况与亲水表面、中性表面的情况类似.在逐渐挤过障碍物的过程中,气泡会因障碍物表面亲气而吸附在障碍物表面上,在障碍物表面形成一层气膜.在通过障碍物最狭窄部分,也会产生两个对称的气孔,与障碍物表面为中性情况相比,气孔产生的位置更靠近下壁面,并且气孔的尺度更大.随着气泡的上升,气孔的尺寸越来越大,当气泡运动到障碍物上方时,气泡的两个对称的小触角与障碍物的接触面积较大.在浮力作用下,气泡与障碍物脱离,在气泡下方形成两个狭长的气带,随后在表面张力作用下,这两个气带收缩,气泡以球冠继续运动.

为了进一步研究亲气表面对气泡动力学行为的影响,图7给出障碍物表面为150°时气泡运动情况.

图7 接触角为150°时气泡的运动过程Fig.7 Bubble rising process with the contact angle of 150 °

从图中可以看出,与接触角为120°情况相比,气泡与障碍物接触时气孔变得更大.由于此时吸附力更强,上升的气泡残留在障碍物表面的质量增加,此时障碍物表面上会形成两个对称的小气泡,随着气泡越升越高,障碍物表面的气膜均匀铺展.与表面接触角为120°情况相比,在气泡没有脱离障碍物之前,气泡下方形成的两个触角与障碍物的接触面积更大,而气泡在整体挤过障碍物后,气泡整体的质量更少.

4 结 论

采用格子Boltzmann模型研究了障碍物表面润湿性不同时,微通道内气泡在浮力作用下的界面动力学行为,通过对比分析得出如下结论:

a. 当障碍物表面亲水时,气泡穿过整个通道的速度减小,并且气泡在穿过障碍物的过程中始终与障碍物表面保持4个网格左右的距离,因此,尽管气泡被障碍物挤压严重变形,但是全部气泡都可以顺利穿过障碍物.

b. 障碍物表面中性时,气泡的变形较亲水更明显.

c. 障碍物表面亲气时,气泡穿过障碍物通道时会粘附在障碍物表面,在浮力、表面张力以及粘附力的共同作用下,气泡分裂并严重变形,当气泡穿过障碍物时其质量减少,质量减少的量与壁面润湿性强度相关.

[1] YAN Z,AWRASA M,GIOVANNI Z.Bubble nucleation and cooperativity in DNA melting[J].Journal of Molecular Biology,2004,339(1):67-75.

[2] FEI K,CHENG C H,HONG C W.Lattice boltzmann simulations of CO2bubble dynamics at the anode of a μDMFC[J].Journal of Fuel Cell Science and Technology,2006,3(2):180-187.

[3] FEI K,HONG C W.All-angle removal of CO2bubbles from the anode microchannels of a micro fuel cell by lattice-Boltzmann simulation[J].Microfluidics and Nanofluidics,2007,3(1):77-88.

[4] ALIZADEH M,SEYYEDI S M,RAHNI M T,et al.Three-dimensional numerical simulation of rising bubbles in the presence of cylindrical obstacles,using lattice Boltzmann method[J].Journal of Molecular Liquids,2017,236:151-161.

[5] MAXWORTHYT T,GNANN G,KÜRTEN M,et al.Experiments on the rise of air bubbles in clean viscous liquids[J].Journal of Fluid Mechanics,1996,321:421-441.

[6] UCHIYAMA T,ISHIGURO Y.Experimental study of flow around a circular cylinder inside a cubble plume[J].Advances in Chemical Engineering & Science,2016,6(3):68342.

[7] 董伟,李瑞阳,郁鸿凌.气液两相流中气泡周围电场特性研究[J].上海理工大学学报,2004,26(3):197-201.

[8] VAN BATEN J M,KRISHNA R.CFD simulations of mass transfer from Taylor bubbles rising in circular capillaries[J].Chemical Engineering Science,2004,59(12):2535-2545.

[9] GUO X F,ZHOU Q,LI J,et al.Implementation of an improved bubble breakup model for TFM-PBM simulations of gas-liquid flows in bubble columns[J].Chemical Engineering Science,2016,152:255-266.

[10] CHENG M,HUA J S,LOU J.Simulation of bubble-bubble interaction using a lattice Boltzmann method[J].Computers and Fluids,2009,39(2):260-270.

[11] LI W Z,DONG B,SUN Y J,et al.Numerical simulation of a single bubble sliding over a curved surface and rising process by the lattice Boltzmann method[J].Numerical Heat Transfer,Part B:Fundamentals,2014,65(2):174-193.

[12] HE X Y,CHEN S Y,ZHANG R Y.A lattice Boltzmann scheme for incompressible multiphase flow and its application in simulation of Rayleigh-Taylor instability[J].Journal of Computational Physics,1999,152(2):642-663.

[13] BHATNAGAR P L,GROSS E P,KROOK M.A model for collision processes in gases I:small amplitude processes in charged and neutral one-component system[J].Physical Review,94(3):511-525.

[14] DAVIES A R,SUMMERS J L,WILSON M C T.On a dynamic wetting model for the finite-density multiphase lattice Boltzmann method[J].International Journal of Computational Fluid Dynamics,2006,20(6):415-425.