排水板抽注水淋洗污染液的轴对称消弭简化解析解答

解子腾，雷国辉，施建勇



排水板抽注水淋洗污染液的轴对称消弭简化解析解答

解子腾1, 2，雷国辉1, 2，施建勇1, 2

(1. 河海大学岩土力学与堤坝工程教育部重点实验室，江苏南京，210098；2. 河海大学岩土工程科学研究所，江苏南京，210098)

为简化分析轴对称淋洗条件下土中污染液浓度的消弭过程，借鉴塑料排水板地基固结等应变理论的思想，假定同一深度上污染液浓度的变化速率为其变化速率的平均值，同时依据相关研究成果，忽略竖向渗流和分子扩散作用，采用分离变量法推导得到淋洗过程中任意位置污染液浓度随时间变化过程的简化解析解答，并与现有的解答和室内试验结果进行对比，验证本文简化解答的适用性。研究结果表明：塑料排水板抽、注水淋洗技术显著提高细粒土中污染液浓度的径向消弭速率，竖向渗流和分子扩散作用对污染液浓度消弭的作用影响可以忽略 不计。

塑料排水板；淋洗；细粒土；污染液；简化解析解答

地表土和地下水污染是威胁人类健康和安全以及社会可持续发展的重大隐患，在工业和农业土地开发与利用过程中，地表土和地下水污染问题，已日渐成为亟待有效解决的环保课题[1−2]，其重要程度不亚于大气污染所造成的气候恶化问题。运用生物、物理和化学等多种修复技术，固化、稳定或清除土中的污染质和污染液，是地表土和地下水污染修复的主要方法[3]。其中，在现场采用竖井抽注水方式开展的原位淋洗是一种便利、高效和经济的土中污染液就地修复技术，该技术开发的初期主要采用较大直径的竖井清除渗透系数较高的粗粒土中的污染液。针对渗透系数较低的细粒土中污染液修复问题，GABR等[4−5]在1996年通过室内实验和理论研究，提出了采用塑料排水板抽注水方式开展的淋洗技术。该技术通过塑料排水板缩短土中污染液的渗流路径，从而提高淋洗渗透系数较低的细粒土中污染液的清除效率。这与排水固结法地基处理技术中设置塑料排水板排水，以加速地基固结为目的有所不同，淋洗技术则通过保持抽水排水板的抽水速率与注水排水板的注水速率相等，以避免地基固结及其对排水板通水能力的影响。排水板抽注水淋洗技术的应用研究已经取得了一些室内试验和现场试验成果[4−16]，但是，与固结解析理论丰富的研究成果相比，对于淋洗技术中污染液消弭过程的解析理论研究尚显捉襟见肘。GABR等[4−5]最早将排水板抽注水淋洗过程简化为轴对称问题，基于水动力弥散微分方程，推导了污染液消弭过程的解析解答。不过，该解答将竖向抽水边界设置于径向无穷远处，将水平边界也设置于无穷深处，模拟的是半无限地基中无限深的抽注水排水板，在中心注水、无限远处抽水的工况，与实际工程中的抽注水排水板的布置条件并不相符，无法反映排水板深度和间距对污染液淋洗效率的影响。王恒宇等[17−19]指出了GABR等[4−5]提出的解答中所采用的抽注水边界条件存在的问题，开创性地建立了合理的抽注水边界条件，并推导了有限边界情况下一维(水平向)、二维和轴对称淋洗工况下的污染液消弭过程解析解答，极大地促进了排水板抽注水淋洗技术解析理论的发展。不过，其轴对称淋洗工况下的解答采用Laplace变换和逆变换法求解，相对较为复杂，涉及特征根的求解，为探索更便于工程师应用、且满足计算精度要求的简化解答，本文作者基于王恒宇等[17−19]提出的解答，借鉴塑料排水板地基固结等应变解析理论的思想[20]，假定同一深度上污染液浓度的变化速率为其变化速率的平均值，同时依据相关的研究成果，忽略对污染液消弭影响较小的竖向渗流和分子扩散作用[21−22]，采用分离变量法推导得到轴对称淋洗工况下污染液消弭的简化解析解答，并与王恒宇等[17−19]的实验和解析计算结果进行对比，验证本文所提出的基本假设和相应的简化解答的适用性。

1 计算模型与基本假设

参照GABR等[4−5]和王恒宇等[17−19]的研究结果，轴对称淋洗工况的物理模型如图1所示，图中，抽水排水板与注水排水板间隔布置，任取1个注水排水板及其周边的抽水排水板得到基本计算模型如图2所示，运用王恒宇等[17−19]提出的等效方法，将注水板周边的抽水板等效为环形抽水墙，从而推求轴对称条件下污染液消弭的解析解答。图2所示计算模型中污染液消弭的水动力弥散微分方程为[4−5, 17−19]下污染液消弭的解析解答。图2所示计算模型中污染液消弭的水动力弥散微分方程为[4−5, 17−19]

(a) 平面布置；(b) 三维布置

图2 轴对称淋洗问题的计算模型

式中：和分别为径向和竖向坐标(如图2所示)；为时间；为土中污染液的浓度；为土的孔隙率；q和q分别为土中污染液在径向和竖向的渗流速度；D和D分别为土中污染液溶质在径向和竖向的水动力弥散系数；d为土颗粒对污染物溶质的吸附和解吸附作用对其扩散的阻滞因子。

污染液的水动力弥散微分方程式(1)与竖向排水体地基固结微分方程有一定的相似性。轴对称固结理论的分析结果表明，由于塑料排水板大大缩短了径向的排水距离，地基固结以径向为主[21]。类似地，在推求式(1)的简化解析解答时，不妨假设其右端的后2项忽略不计，则式(1)可简化为

其中的物理参数为[4−5, 17−19]

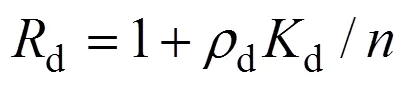
式中：d为土体的干密度；d为与吸附和解吸附作用的相对程度有关的分布系数；0为排水板的注水或抽水速率；为排水板的深度；α为径向弥散度，反映了水动力弥散所起的作用；为污染液在土体中扩散的有效扩散系数，反映了分子扩散在污染液浓度消弭中所起的作用。

根据SHACKELFORD[22]的研究可知：分子扩散仅在渗流速度极低的情况下才会对污染液运移产生较重要的影响。因此，针对塑料排水板抽注水淋洗过程，污染液的径向渗流速度已显著提高，可以近似忽略分子扩散作用的影响，则式(5)可简化为

此外，塑料排水板地基固结解析理论的研究成果表明，自由应变解答与等应变解答所得到的计算结果基本一致，但采用等应变假设可以大大简化微分方程的求解[20]。借鉴这一思路，假定同一深度上污染液浓度的变化速率为其变化速率的平均值，并将式(4)和式(6)代入式(2)，可得本文即将求解的简化的污染液轴对称消弭的水动力弥散微分方程为

其中：

式中：w为排水板的等效半径，可按文献[23−24]提出的方法确定；e为抽、注水排水板之间的间距。

采用王恒宇等[17−19]建立的抽、注水边界条件，顶面和底面边界条件，以及初始条件如下：

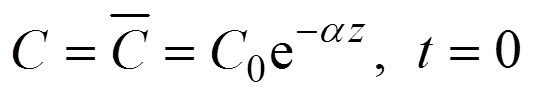
将式(4)和式(6)代入式(9)，注水边界条件可改写为

式(13)中的初始条件考虑了工程实际中污染液初始浓度随深度的衰减情况，因此，虽然微分方程式(7)中忽略了竖向渗流的影响，但污染液的浓度仍然是深度的函数，即(,,)。

2 解答的推导过程

采用分离变量法，污染液浓度可表示为

将其代入式(7)可得

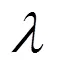
式(17)的通解为

式中：e为自然常数；和为待定常数，可由边界条件求解得到。

将式(19)代入式(15)再代入式(8)可得

其中：

将式(20)代入式(18)可得

式(22)的解为

式中：为待定常数。

将式(19)和(23)代入式(15)可得

将式(24)代入抽水、注水边界条件式(10)和式(14)可得：

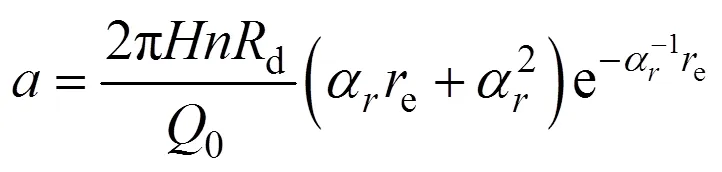
将式(23)代入式(20)再代入初始条件式(13)可得

最后，将式(25)～(27)代入式(24)可得

从式(28)可以看出：本文提出的轴对称淋洗工况下的简化解析解答的表达式形式简便，只需采用简便的计算软件如Excel或计算工具如电子计算器等就可以得到抽、注水淋洗过程中任意时刻、任意位置处的污染液浓度。

工程实践中，通常依据淋洗渗出液浓度的测试结果来评判淋洗效果，理论上，则可以采用=0 m处污染液的平均浓度来进行分析。为此，将式(23)代入式(20)并依据式(27)可得=0 m处污染液的平均浓度随时间的变化关系为

3 解答的对比与验证

王恒宇等[17−18]提出的解答是在考虑竖向渗流和分子扩散作用的基础上，针对微分方程式(1)，即考虑同一深度上污染液浓度的变化速率不同而求得的。该解答在理论上是完备的，不过，相对较为复杂的利用特征根求解的计算过程也增加了工程应用的难度，这与固结理论中的自由应变解答不便于工程应用具有一定的相似性。本文提出的简化解答是在借鉴固结理论等应变解答的思想，假定同一深度上污染液浓度变化速率相同，同时忽略对污染液消弭影响较小的竖向渗流和分子扩散作用的基础上，通过微分方程式(7)推导得到的。为验证本文简化解答和基本假设的适用性，将本文解答与王恒宇等[17−18]提出的解答进行对比。同时，也与王恒宇[17]的室内试验结果以及PARK等[14]的试验结果进行对比。

3.1 与王恒宇等[17−18]解答的对比

图3 本文简化解答与王恒宇等[17−18]解答计算结果对比

3.2 与王恒宇[17]的试验结果的对比

3.3 与PARK等[14]的试验结果的对比

图4 本文简化解答与王恒宇[17]的试验及解答对比

图5 本文简化解答与PARK等[14]的试验及解答对比

从图3~5可知：在塑料排水板轴对称淋洗问题的分析中，竖向渗流和分子扩散作用对污染液消弭的作用影响是可以忽略不计的。本文基于该假设条件，以及借鉴固结理论的等应变解答的思想、假定同一深度上污染液浓度的变化速率为其变化速率的平均值，由此推导得到的轴对称淋洗问题的简化解答也具有令人满意的精度。

4 结论

1) 针对塑料排水板轴对称淋洗土中污染液问题，忽略竖向渗流和分子扩散，并假定同一深度上污染液浓度的变化速率为其变化速率的平均值，推导得到了其简化解析解答。

2) 通过与现有的解答以及室内试验结果的对比，验证了本文简化解答的适用性。

3) 细粒土中污染液的塑料排水板轴对称淋洗技术中，污染液浓度的径向消弭速率是其主要影响因素，竖向渗流和分子扩散作用对污染液消弭的作用影响可以忽略不计。

4) 由于现有的轴对称淋洗技术的现场试验报道中参数不明确，本文的简化解析解答与现场试验的对比验证还有待于进一步的研究。

[1] 陈永贵, 贺勇, 周星志. 压实膨润土工程屏障对重金属污染物的阻滞[J]. 中南大学学报(自然科学版), 2012, 43(10): 4038−4043. CHEN Yonggui, HE Yong, ZHOU Xingzhi. Retention of heavy metal ion on engineering barriers of compacted bentonite[J]. Journal of Central South University (Science and Technology), 2012, 43(10): 4038−4043.

[2] 吴珣, 施建勇, 何俊. 考虑降解时有机污染物在完好复合衬垫中的扩散分析[J]. 中南大学学报(自然科学版), 2015, 46(12): 4725−4731. WU Xun, SHI Jianyong, HE Jun. Analysis of organic contaminant diffusion through intact composite liners considering degradation[J]. Journal of Central South University (Science and Technology), 2015, 46(12): 4725−4731.

[3] 杜延军, 金飞, 刘松玉, 等. 重金属工业污染场地固化/稳定处理研究进展[J]. 岩土力学, 2011, 32(1): 116−124. DU Yanjun, JIN Fei, LIU Songyu, et al. Review of stabilization/solidification technique for remediation of heavy metals contaminated lands[J]. Rock and Soil Mechanics, 2011, 32(1): 116−124.

[4] GABR M A, BOWDERS J J, WANG J, et al. In situ soil flushing using prefabricated vertical drains[J]. Canadian Geotechnical Journal, 1996, 33(1): 97−105.

[5] GABR M A, WANG J, BOWDERS J J. Model for efficiency of soil flushing using PVD-enhanced system[J]. Journal of Geotechnical Engineering, ASCE, 1996, 122(11): 914−919.

[6] QUARANTA J D, GABR M A, SZABO D, et al. Characteristics and performance of prefabricated vertical drains for enhanced soil flushing[J]. Transportation Research Record, 1997, 1596(1): 93−100.

[7] GABR M A, SABODISH M, WILLIAMSON A, et al. BTEX extraction from clay soil using prefabricated vertical drains[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 1999, 125(7): 615−618.

[8] QUARANTA J, SABODISH M, GATES K, et al. Enhanced subsurface flushing of mixed waste: A field study[C]// ZIMMIE T F. Environmental Geotechnics. Geotechnical Special Publication No. 105. Reston: American Society of Civil Engineers, 2000, 132−141.

[9] WELKER A L, GILBERT R B. A bench scale PVD remediation system experiment[J]. Waste Management, 2002, 22(7): 791−801.

[10] WELKER A L, GILBERT R B. Calibration of flow and transport model with a bench-scale prefabricated vertical drain remediation system[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2003, 129(1): 81−90.

[11] WARREN K A, GABR M A. Liquid extraction using prefabricated vertical wells (PVWs) under vacuum in clay[J]. Geotechnical Testing Journal, ASTM, 2005, 28(4): 328−335.

[12] WARREN K A, GABR M A, QUARANTA J D. Field study to investigate WIDE technology for TCE extraction[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2006, 132(9): 1111−1120.

[13] SHARMIN N, KUNBERGER T, GABR M A, et al. Performance modeling and optimization of contaminant extraction using prefabricated vertical wells (PVWs)[J]. Geosynthetic International, 2008, 15(3): 205−215.

[14] PARK J J, SHIN E C. Applicability of soil flushing remediation system for contaminated fine-grained soils using PVDs[J]. International Journal of Geotechnical Engineering, 2009, 3(3): 417−427.

[15] SHARMIN N, GABR M A. Optimized prefabricated vertical wells for light nonaqueous phase liquid recovery[J]. Canadian Geotechnical Journal, 2012, 49(12): 1434−1443.

[16] GABR M A, SHARMIN N, QUARANTA J D. Multiphase extraction of light non-aqueous phase liquid (LNAPL) using prefabricated vertical wells[J]. Geotechnical and Geological Engineering, 2013, 31(1): 103−118.

[17] 王恒宇. 竖井淋洗修复污染地基的研究[D]. 杭州: 浙江大学建筑工程学院, 2015: 45–68. WANG Hengyu. A study for contaminant extraction in polluted soil using PVD-enhanced system[D]. Hangzhou: Zhejiang University. College of Civil Engineering and Architecture, 2015: 45–68.

[18] WANG Hengyu, TANG Xiaowu, TANG Qiang, et al. An analytical solution for contaminant extraction in a radial flow field using PVD-enhanced system[J]. Geosynthetics International, 2016, 23(1): 23–35.

[19] TANG Xiaowu, WANG Hengyu, WANG Yan, et al. An analytical solution for contaminant extraction using well injection depth extraction technology[J]. Geotextiles and Geomembranes, 2015, 43(2): 118−127.

[20] LEI Guohui, XU Lidan, ZHENG Qiang, et al. Role of equal-strain assumption in unit-cell theory for consolidation with vertical drains[J]. Journal of Central South University, 2017, 24(12): 2914–2923.

[21] LEI Guohui, ZHENG Qiang, NG C W W, et al. An analytical solution for consolidation with vertical drains under multi-ramp loading[J]. Géotechnique, 2015, 65(7): 531−547.

[22] SHACKELFORD C D. The ISSMGE Kerry Rowe lecture: the role of diffusion in environmental geotechnics[J]. Canadian Geotechnical Journal, 2014, 51(11): 1219−1242.

[23] ABUEL-NAGA H, BOUAZZA A. Equivalent diameter of a prefabricated vertical drain[J]. Geotextiles and Geomembranes, 2009, 27(3): 227−231.

[24] ABUEL-NAGA H M, BOUAZZA A, BERGADO D T. Numerical assessment of equivalent diameter equations for prefabricated vertical drains[J]. Canadian Geotechnical Journal, 2012, 49(12): 1427−1433.

(编辑 杨幼平)

A simplified analytical solution for axisymmetrical dispersion of liquid contaminant due to flushing with PVDs

XIE Ziteng1, 2, LEI Guohui1, 2, SHI Jianyong1, 2

(1. Key Laboratory of Ministry of Education for Geomechanics and Embankment Engineering,Hohai University, Nanjing 210098, China;2. Geotechnical Research Institute, Hohai University, Nanjing 210098, China)

In order to simplify the analysis of the dispersion process of concentration of liquid contaminant in soil under axisymmetrical flushing conditions, the rate of variation of the concentration of liquid contaminant at the same depth was assumed to be the average value at that depth. This assumption was made with the reference to the idea of equal strain theory of ground consolidation with prefabricated vertical drains(PVDs). Meanwhile, the effects of vertical seepage and molecular diffusion were ignored based on relevant research outcomes. A simplified analytical solution to the process of variation of concentration of liquid contaminant at any arbitrary position with time was derived using the method of separation of variables. Calculated results were compared with the results from the available solutions and laboratory experiments. The applicability of the proposed solution in this study was verified. The results show that the radial dispersion rate of concentration of liquid contaminant in fine-grained soil is significantly improved by the flushing technique with water injection and extraction using PVDs. The influence of vertical seepage and molecular diffusion on the dispersion of concentration of liquid contaminant can be ignored.

prefabricated vertical drain; soil flushing; fine-grained soil; liquid contaminant; simplified analytical solution

X53

A

1672−7207(2018)01−0201−07

10.11817/j.issn.1672-7207.2018.01.026

2016−03−04；

2016−05−10

国家自然科学基金资助项目(51278171，41530637)；中央高校基本科研业务费专项资金资助项目(2015B06014，2017B20614) (Projects(51278171, 41530637) supported by the National Natural Science Foundation of China; Projects(2015B06014, 2017B20614) supported by the Fundamental Research Funds for the Central Universities of China)

雷国辉，博士，教授，从事土力学与地基基础工程研究；E-mail: leiguohui@hhu.edu.cn