燃气轮机叶片精铸蜡型陶芯夹紧元件布局优化研究

朱金焰，陆长哥，张仲杰

(上海步朗电子科技有限公司 研发中心，上海 200235)

0 引 言

高性能燃气涡轮发动机(航空发动机及地面燃气轮机)是国防重大装备的“心脏”[1-3]。为了进一步提升燃气轮机的效率，需要提高涡轮前进口温度[4]，为此必须增加涡轮叶片的耐高温能力。目前，涡轮叶片普遍采用复合气膜冷却单晶空心涡轮叶片技术提高其承温能力。涡轮叶片壁厚对叶片冷效及寿命具有决定性影响，K.Winens[5]通过对四种不同型号涡轮叶片失效模式的统计分析，认为壁厚是导致叶片失效最主要原因。制备壁厚精度合格的精铸蜡型是保证涡轮叶片壁厚的首要条件，而精铸蜡型壁厚主要依靠精确控制陶芯在蜡型模具中的位姿进行保证。通常在模具中设计定位元件及夹紧元件对陶芯空间位姿进行约束及调整[6]，其中定位元件主要控制和调整陶芯位姿，夹紧元件主要约束陶芯在充型过程的漂移。

通过陶芯定位元件的布局优化设计，可增强其定位稳定性，弱化陶芯及定位元件制造过程中的误差对定位匹配精度的影响。崔康等[6]提出了基于蜡型壁厚测量结果的定位元件逆向调整方法，通过建立陶芯逆向调整模型，确定了陶芯壁厚偏差与定位元件补偿量之间的映射关系，依据壁厚测量结果逆向调整陶芯定位元件，从而控制蜡型壁厚分布。Jiang R S等[7]通过分析陶芯定位误差传递链，建立了陶芯定位误差传递模型，并进一步基于D-Optimality方法，实现了陶芯定位元件的布局优化。冯炜等[8]引入壁厚权值约束的匹配算法，实现了陶芯测量数据与蜡型模具型面的精确匹配；基于匹配结果建立了定位元件的尺寸计算方法，实现了陶芯位姿调整。

针对陶芯夹紧元件的优化问题，崔康等[9]提出了一种基于空间形封闭模型的夹紧点布局优化方法，以满足空间形封闭以及陶芯与夹紧元件接触压力要求为约束条件，实现了夹紧元件的优化。此外，在工件夹持问题上，K.P.Padmanaban[10-11]及F.M.T.Rex[12]分别以夹紧元件载荷、工件表面型值点变形量以及工件弹性位移作为优化目标，分别利用有限元仿真技术与启发式算法给出工件定位夹紧布局的详细优化策略。由于陶芯存在制造误差，且陶芯材料具有硬脆性，夹紧元件与陶芯之间需保留一定间隙(通常为0.1 mm)，以保证陶芯在充型过程中的强压应力状态下具有适度退让性。由于该间隙的存在，使得陶芯在蜡料填充型腔时受蜡料流动影响在狭小的空间内易产生运动漂移，引起蜡型壁厚偏差。然而，上述研究并未针对该问题展开探讨。

本文针对空心涡轮叶片精铸蜡型制备过程中陶芯漂移引起壁厚偏差这一问题展开研究。首先对陶芯在蜡料流场作用下的载荷进行分析，进而计算陶芯在蜡料载荷和夹紧元件不完全约束下的运动漂移，建立夹紧元件布局与陶芯漂移的映射关系；在此基础上，以陶芯漂移引起的壁厚偏差为目标，建立夹紧元件布局优化模型，并通过改进的遗传算法优化夹紧元件的位置，以期控制蜡型壁厚偏差。

1 陶芯载荷计算方法

蜡型充型过程是非牛顿流体的非等温、非稳态流动过程，基于连续介质理论可推导得出粘性流体动力学的基本方程，该方程可用来描述蜡料填充模具型腔的流动过程。

(1)

(2)

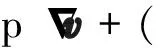
(3)

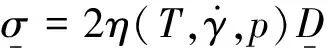
(4)

ρ=ρ(p,T)

(5)

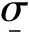
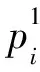
fi=∬pxyds

(6)

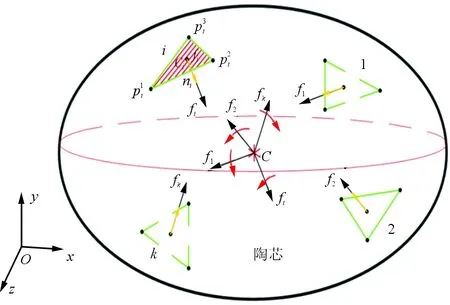
图1 陶芯受力计算示意图Fig.1 Illustration of force computing for ceramic core

计算三角形单元i的重心坐标，并根据该重心坐标从几何模型中提取其法向矢量ni，即可获得蜡料与陶芯接触区域三角形单元i上的等效力矢量fi。

fi=fini

(7)

将蜡料与陶芯接触区域各三角形单元的矢量力fi合成到陶芯的重心C处，即可获得该时刻陶芯的合力FC及合力矩MC：

∑fi=FC
∑MC(fi)=MC

(8)

最后，将充型各离散时刻的合力及合力矩进行插值，即可获得陶芯的充型载荷函数。

2 陶芯漂移计算方法

计算得出陶芯在充型过程中的载荷后，即可基于刚体运动学理论，研究陶芯的漂移计算方法。当陶芯运动过程中与夹紧元件或定位元件接触碰撞时，针对碰撞力的计算，采用弹簧阻尼接触碰撞模型计算碰撞力。该模型假设变形发生在接触点的附近区域，借助弹簧阻尼系统，将瞬态的接触碰撞问题转化为连续的动力学过程进行求解，如图2所示，接触碰撞力可表示为

(9)

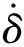
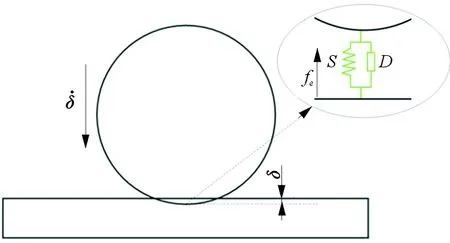
图2 弹簧阻尼接触碰撞模型示意图Fig.2 Spring-damping force model

由于定位元件和夹紧元件的不完全位置约束，陶芯在狭小空间内受力做空间自由运动。处于自由运动状态的陶芯具有六个方向的自由度，所以需要六个参数描述其在空间中的运动。陶芯的自由运动可以分解为刚体随着其质心的平移运动和相对于质心的定点转动。

陶芯在定位元件和夹紧元件不完全约束下的平移运动方程的矢量形式为

(10)

式中：∑F为作用在陶芯上的合力；FC为蜡料流动对陶芯的作用力；fe为陶芯与夹紧元件或定位元件的接触碰撞力；G为陶芯受到的重力。

选择与陶芯固连且随陶芯运动的坐标系作为动坐标系Cx′y′z′，在运动过程中，陶芯相对于坐标轴的转动惯量和惯性积将保持恒定，故陶芯转动的动力学方程可表示为矢量形式。

(11)

式中：∑M为作用在陶芯质心上的合力矩；HC为陶芯质心的角动量；ω为陶芯绕固连坐标轴x′,y′,z′轴的角速度。

通过求解方程组(10)和方程组(11)得到陶芯质心处的平移矢量Γ=Δr=[Δx,Δy,Δz]T和绕动坐标系的转动矢量Θ=[φ,θ,φ]T。

3 夹紧元件布局优化方法

3.1 夹紧元件布局优化模型

因夹紧元件布局不同，使得陶芯受蜡料流动作用力所产生的漂移量不同，令Cj(j=0,1,…,i)为夹紧元件，其位置矢量为Cj；设Ω为对应于某种夹紧方案的运动漂移量，Ω=[Δx,Δy,Δz,φ,θ,φ]T。以夹紧元件位置组合C=(C1,C2,…,Ci)为自变量，则夹紧元件布局C为自变量集合X中元素；运动漂移量Ω为因变量集合Y中的元素，其他条件视为理想状况。按照第2节刚体动力学分析的对应法则fRDA，集合X中的每一个元素(夹紧元件布局方案C)，在集合Y中都有唯一的元素(运动漂移量Ω)与其对应，则有从X到Y的映射：

fRDA∶X→Y

(12)

元素C在映射fRDA下对应的像Ω：

Ω=fRDA(C1,C2,…,Ci)

(13)

在陶芯型面上取监测点Pj，设Pj0为其初始位置矢量，Pjt为其在陶芯运动漂移后位置矢量，则该监测点的位移大小为

Dj(Ω)=|Pjt-Pj0| (j=1,…,k)

(14)

在陶芯型面上选取k个监测点，以其位移大小之和衡量陶芯的运动漂移量(即将六个分量的陶芯运动漂移量Ω转化为一个量)，并以该位移和最小为优化目标求解使陶芯运动漂移最小的夹紧元件布局，描述为

(15)

3.2 布局优化模型求解

求解优化的夹紧元件布局方案使得陶芯的运动漂移量最小，该问题可归结为最优化问题。在3.1节的优化模型中，除了自变量集合、对应法则和因变量集合外，无法获得陶芯的曲面方程、截面线方程以及搜索的梯度等精确信息，难以采用基于梯度信息的确定性优化算法，故本文采用改进的遗传算法求解夹紧元件的优化布局方案 。以夹紧元件的位置为自变量，刚体动力学分析为对应法则，获得对应于一种夹紧元件布局下的陶芯运动漂移情况。针对如图3所示的陶芯，考虑工艺要求设置夹紧元件候选点，每一个夹紧元件的编号为一个基因，故共5个基因；依次排列夹紧元件的位置编号(“基因”)为一个“染色体”，即一个个体；并以随机生成的N个个体为初始种群。

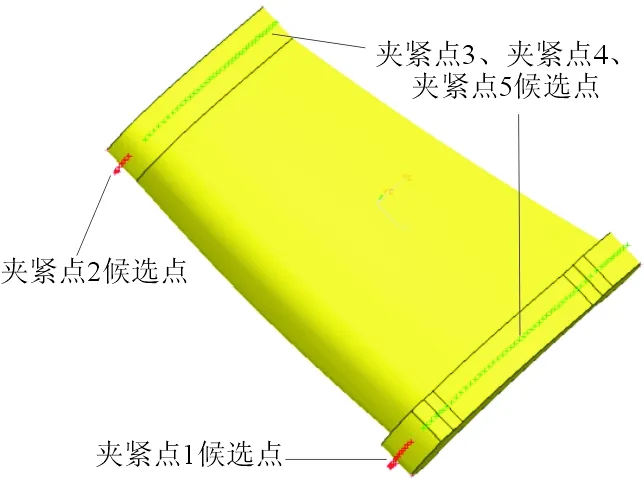
图3 夹紧元件分布及候选点示意图Fig.3 Diagram of the clamping rods and their candidate locations

标准遗传算法[15]是按照种群中个体对环境的适应能力对其执行选择、交叉和变异等进化操作，以使种群的下一代个体具有更好的适应环境的能力，但易陷入局部最优解、早熟等问题。为此，本文通过对标准遗传算法的算子进行改进，在保持种群多样性的同时提高优化效率。

(1) 选 择

选择操作是从当代种群中挑选适应环境能力强的个体以便对其基因进行后续的遗传操作，以使种群中的优良基因能够被保留至后代。本文采用基于排序的轮盘赌选择策略，可描述为：将个体数为n的群体按照其个体适应度值由小到大的顺序排成一个序列，如果个体i的排序序号为rankfitness(i)，则其被选择概率：

(16)

(2) 交叉和变异

交叉和变异操作主要由交叉概率Pc和变异概率Pm控制，而Pc和Pm值的大小直接影响算法的收敛性。本文采用基于Sigmoid函数的交叉和变异概率调整策略，使得算法尽快跳出局部收敛。

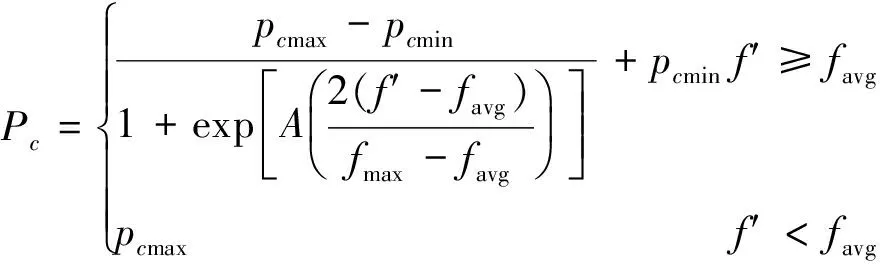
(17)

4 实例验证及讨论

本文以如图4所示蜡型为对象，对其充型过程进行计算分析。蜡料采用Argueso Cerita wax F30-75进行分析，其材料数据由Moldflow Corp测定；充型工艺参数如表1所示。通过提取充型各时刻接触面网格节点压强值，利用充型载荷计算模型获得陶芯的载荷分布曲线，如图5所示。

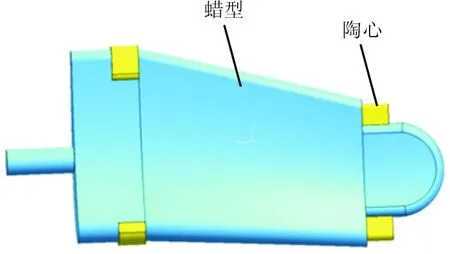
图4 蜡型示意图Fig.4 Diagram for wax pattern

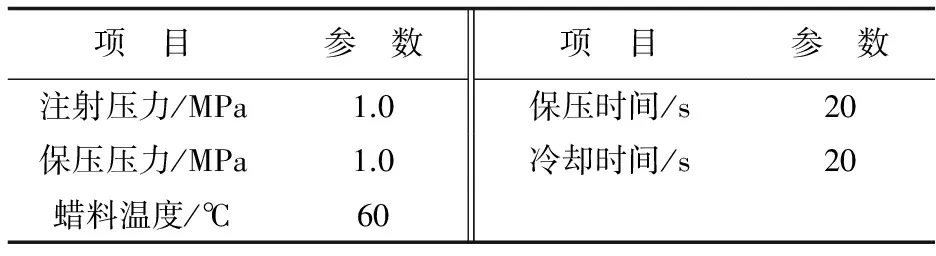
项 目参 数项 目参 数注射压力/MPa1．0保压时间/s20保压压力/MPa1．0冷却时间/s20蜡料温度/℃60

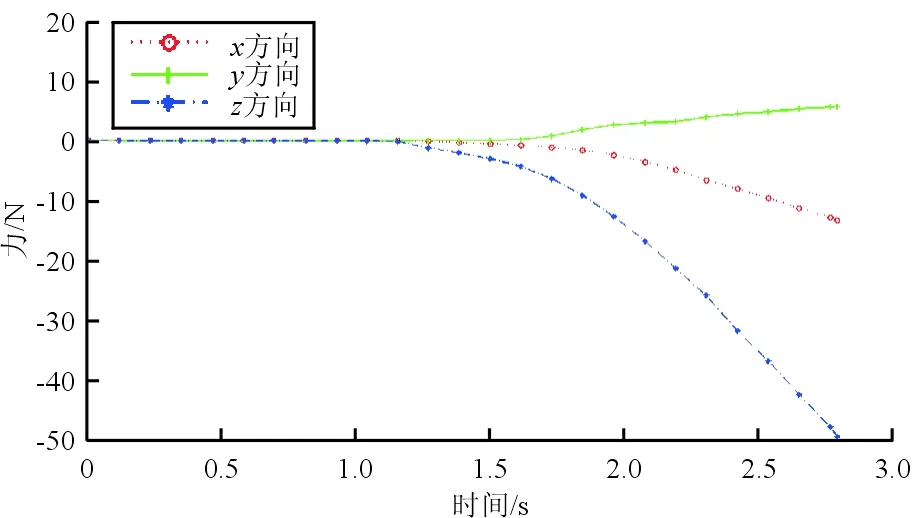
(a) 合力

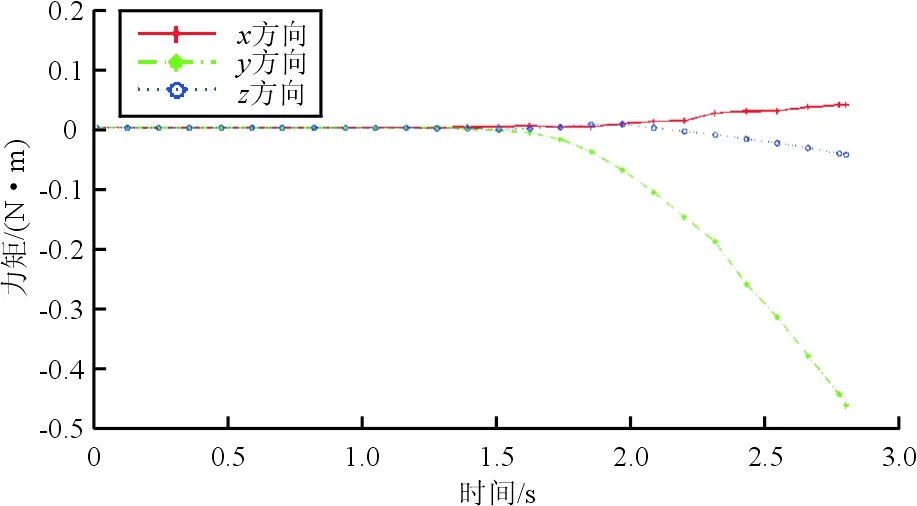
(b) 合力矩图5 压蜡过程陶芯载荷分布Fig.5 Load diagram of wax injection process

以图4所示蜡型为对象，从叶尖至叶根方向等间距取22条截面线(如图6所示)，检查陶芯在载荷作用下产生的漂移对叶片内表面偏差的影响，并以此作为量化依据对陶芯夹紧元件进行优化。

图6 漂移评价截面示意图Fig.6 Diagram of shifting evaluation cross sections

工程实践中，夹紧元件布局是与定位元件位置对称分布确定的，如图7(a)所示；根据本文提出的陶芯夹紧元件布局优化算法计算的优化的夹紧元件布局方案如图7(b)所示。在叶尖和叶根区域，优化后的定位元件和夹紧元件分别为两侧加中间分布，即“三角形”分布，更加有效、稳固。该优化方案下，以陶芯质心为基点，计算得最终的运动漂移量为Ω=[Δx,Δy,Δz,ψ,θ,φ]T=[-0.090 4,0.014 7,-0.015 3,-3.376 6,0.067 1,3.440 0]T。

按照图6所示截面方案，对夹紧元件布局方案优化前和优化后的内腔截面偏差进行评价，优化后与优化前的夹紧元件布局效果相比，陶芯漂移量减小，蜡型内腔截面线最大偏差和平均偏差均明显减小，具体数值如表2所示。

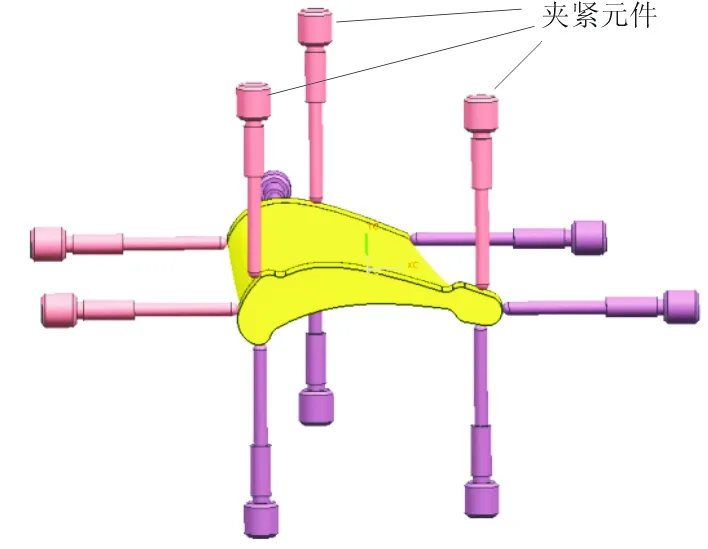
(a) 优化前夹紧元件布局图

(b) 优化后夹紧元件布局图图7 夹紧方案对比Fig.7 Comparison of clamping rods layout

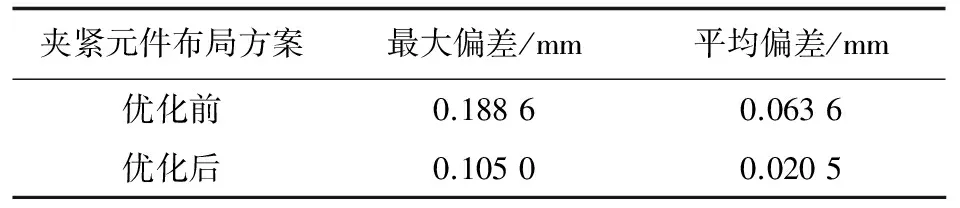
夹紧元件布局方案最大偏差/mm平均偏差/mm优化前0．18860．0636优化后0．10500．0205

从表2可以看出：该夹紧元件布局优化方案可以减小空心叶片蜡型内表面型面偏差，从而能够提高蜡型壁厚精度。

5 结 论

(1) 通过陶芯在蜡料流场作用下的合力及合力矩计算方法，发现在注蜡方向上的陶芯受力较大，为z轴负方向，x和y方向上合力相对较小。

(2) 基于优化的夹紧元件布局方案，蜡型壁厚最大偏差下降了约44%，平均偏差下降了约68%，从而实现了壁厚偏差的控制，表明本文所提的陶芯夹紧元件优化方法可以有效控制陶芯的运动漂移，降低了蜡型壁厚偏差。

[1] 刘大响, 陈光, 等. 航空发动机——飞机的心脏[M]. 北京: 航空工业出版社, 2003: 1-5.

Liu Daxiang, Chen Guang, et al. Aero-engine-Heart of airplane[M]. Beijing: Aviation Industry Press, 2003: 1-5.(in Chinese)

[2] 雷杰, 苏三买, 周顾庭, 等. 民用涡扇发动机结构与建模分析研究[J]. 航空工程进展, 2013, 4(4): 450-457.

Lei Jie, Su Sanmai, Zhou Guting, et al. Investigation of civil turbofan structure and components modeling[J]. Advances in Aeronautical Science and Engineering, 2013, 4(4): 450-457.(in Chinese)

[3] 刘伟, 陈玉春, 贾琳渊, 等. 基于技术参数评估的涡扇发动机总体性能设计[J]. 航空工程进展, 2014, 5(3): 312-319.

Liu Wei, Chen Yuchun, Jia Linyuan, et al. Turbofan engine performance design based on technical parameters evaluation[J]. Advances in Aeronautical Science and Engineering, 2014, 5(3): 312-319.(in Chinese)

[4] 商体松, 赵明, 涂冰怡. 航空发动机燃烧室冷却结构的发展及浮动壁结构的关键技术[J]. 航空工程进展, 2013, 4(4): 407-413.

Shang Tisong, Zhao Ming, Tu Bingyi. Development of aero-engine combustor cooling structure and the key technologies of floating-wall[J]. Advances in Aeronautical Science and Engineering, 2013, 4(4): 407-413.(in Chinese)

[5] Winens K. Airfoil thickness as a life limiting factor of gas turbine blades[C]. In 20th Symposium of the Industrial Application of Gas Turbines Committee Banff, Alberta, Canada, 2013: 1-14.

[6] 崔康, 汪文虎, 蒋睿嵩, 等. 涡轮叶片精铸模具陶芯定位元件逆向调整算法[J]. 航空学报, 2011, 32(10): 1924-1929.

Cui Kang, Wang Wenhu, Jiang Ruisong, et al. Reverse adjustment algorithm of ceramic core locators in hollow turbine blade investment casting die[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(10): 1924-1929.(in Chinese)

[7] Jiang R S, Wang W H, Zhang D H, et al. Wall thickness monitoring method for wax pattern of hollow turbine blade[J]. International Journal of Advanced Manufacturing Technology, 2016, 83(5-8): 949-960.

[8] 冯炜, 汪文虎, 王孝忠, 等. 空心涡轮叶片精铸蜡型陶芯定位元件尺寸计算方法[J]. 航空学报, 2013, 34(1): 181-186.

Feng Wei, Wang Wenhu, Wang Xiaozhong, et al. Size calculation method of ceramic core locators for hollow turbine blade investment casting wax pattern[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(1): 181-186.(in Chinese)

[9] 崔康, 汪文虎, 蒋睿嵩, 等. 空心涡轮叶片精铸模具陶芯夹紧布局优化方法[J]. 计算机集成制造系统, http:∥kns.cnki.net/kcms/detail/11.5946.TP.20171110.1101.006.html.

Cui Kang, Wang Wenhu, Jiang Ruisong, et al. Optimization method for clamping layout of ceramic core in wax pattern die of hollow turbine blade[J]. Computer Integrated Manufacturing Systems, http:∥kns.cnki.net/kcms/detail/11.5946.TP.20171110.1101.006.html.(in Chinese)

[10] Padmanaban K P, Prabhaharan G. Dynamic analysis on optimal placement of fixturing elements using evolutionary techniques[J]. International Journal of Production Research 2008, 46(15): 4177-4214.

[11] Padmanaban K P, Arulshri K P, Prabhaharan G. Machining fixture layout design using ant colony algorithm based continuous optimization method[J].The International Journal of Advanced Manufacturing Technology, 2009, 45(9-10): 922-934.

[12] Rex F M T, Ravindran D. An integrated approach for optimal fixture layout design[J]. Journal of Engineering Manufacture, 2017, 231(7): 1217-1228.

[13] Bakharev A, Fan Z, Han S, et al. Prediction of core shift effects using mold filling simulation[C]. In ANTEC Conference Proceedings, vol.LXII, Society of Plastics Engineers. New Jersey: Brookfield, 2004: 621-625.

[14] Wang N, Wang W H, Jiang R S, et al. Ceramic core shifting monitoring through clamping rods optimization for wax pattern of turbine blade[J]. The International Journal of Advanced Manufacturing Technology, 2017, 91(5-8): 2193-2204.

[15] Michalski R S, Carbonell J G, Mitchell T M. Machine learning: An artificial intelligence approach[M]. New York: Springer Science & Business Media, 1983: 7-9.