Supersonicflow over a pitching delta wing using surface pressure measurements and numerical simulations

Mostafa HADIDOOLABI,Hossein ANSARIAN

Aerospace Engineering Department,Malek Ashtar University of Technology,Tehran 158751774,Iran

1.Introduction

Delta wings are used in many aircraft whichfly at supersonic speeds.Airplanes and space planes with the delta wing oftenfly at high angles of attack,especially at takeoff or landing phases,where their aerodynamic performance at low speed is weak.Moreover,flying at high angles of attack even at transonic and supersonic regimes can be expected for future space planes at the reentry phase.As the maneuverability of such aircraft is enhanced,the comprehension of the nature of unsteadyflows around delta wings and the associated phenomena such as vortex breakdown and vortex-shock patterns becomes more important.

It is well known that in the steadyflight of a delta wing a shear layer is separated from the leading edge which produces two counter-rotating vortices on the leeside of the wing.This results in the production of large suction peaks and thereby the generation of lift.Two much smaller vortices with opposite sense of rotation relative to primary vortices,the secondary vortices,are also formed under certainflow conditions.At sufficiently high angles of attack,the leading edge vortices above a delta wing undergo a vigorous form offlow discontinuity known as vortex breakdown.This phenomenon is characterized by vortex core inflation,internalaxial flow stagnation,and substantial fluctuations in flow variables downstream.

Vorticalflow structure and vortex breakdown on stationary delta wings at incompressible regime has been the focus of a great deal of effort.Gursul1,2presented extensive reviews of the steady and unsteady aerodynamics of delta wingsflying at low speeds.The unsteadyflow structure on a delta wing undergoing maneuverhasreceived lessattention.Such researches are motivated by the need to enhance the maneuver capabilities of current and future combat airplanes,missiles and spacecraft.

Rockwell3and Visbal4reviewed the unsteady aspects offlow structures and vortex breakdown on delta wings.Usingflow visualization techniques,Maltby et al.5investigated theflow phenomena over delta wings subjected to the heaving oscillation and found the phase lag existing in the variations of vortex core position compared to its static case.Lambourne et al.6studied the behavior of the leading edge vortices over a delta wing following a sudden change of incidence.By performingflow visualization on a delta wing with pitching oscillation,Gad-el-Hak and Ho7showed the growth-decay cycles for the leading edge vortices as well as the hysteresis loops inflow patterns.Gursul and Yang8showed that the phase lag of the vortex breakdown position on the pitching wing may be related to the adverse pressure gradient and its variations on the wing surface,based on the suggestion of Gursul and Ho9that vortex breakdown over delta wings in unsteadyflow is caused by the external pressure gradient.Visbal and Gordnier10computationally investigated the effect of pitch axis location and pitch rate on the onset of vortex breakdown.Atta and Rockwell11and LeMay et al.12characterized the response offlow pattern on a delta wing to a pitching oscillation.Magness et al.13investigated the instantaneous crossflow topologies of the unsteady leading edge vortices on a delta wing at high angles of attack.The leading edge vortex was found to exhibit an outward-spiraling motion corresponding to an unstable focus.Lin and Rockwell14defined the region of vortex breakdown in terms of patterns of azimuthal vorticity,as well as critical points of the sectional topology.Gursul15proposed an explanation for time lag based on the theory of vortex breakdown being a wave propagation phenomenon.

Yavuz et al.16investigated the near-surface topology andflow structure on a moderate sweep angle delta wing during the relaxation.Goruney and Rockwell17studied the time evolution of the near-surface topology on a delta wing of moderate sweep angle during relaxation of theflow after termination of a pitching maneuver for a wide range of pitch rates.Liu et al.18used and Improved Delayed Detached Eddy Simulation(IDDES)method based on the Shear Stress Transport(SST)k-ω turbulence model to predict the unsteady vortex breakdown past an 80°/65°double-delta wing.They analyzed thefluctuations of mean lift,drag,pitching moment,pressure coefficients,and breakdown locations.

Most studies of unsteady vorticalflow structure on oscillating delta wings have been done for incompressibleflows or forflows with very low free-stream Mach number.As a result,little is known about the behavior of theflow pattern and structure on a pitching delta wing at higher Mach numbers,especially at supersonic speeds.At supersonic velocities,there may be variousflow regimes on the leeward side of delta wings,which differ by the number and positions of streamwise vortices,internal shock waves,and other features of theflow.Stanbrook and Squire19proposed the earliest classification for theflow patterns based on the component of Mach number normal to the leading edge and the component of angle of attack normal to the leading edge.They introduced two types offlows:attached flow and separated flow at the leading edge.Miller and Wood20investigated theflow patterns over delta wings with various sweep angles using several visualization methods and introduced six types offlow patterns based on the possible presence of primary and secondary vortices and shock waves.Szodruch and Peake,21Seshadri and Narayan,22Brodetsky and Shevchenco,23and Brodetsky et al.24examined the flow structure in more detail and suggested similar classifi-cations.Imai et al.25conducted computational simulations offlow field over a 65°sweep delta wing and investigated theflow mechanism behind the flow classification at high angles of attack in transonic and supersonic regimes.Oyama et al.26performed wind tunnel experiments to examine the effect of Mach number onflow structure over a delta wing with blunt leading edges in supersonic and high angle of attack regions.

Literature review shows that there have not been significant researches,either computationally or experimentally performed for unsteady aspects of supersonicflow over delta wings.There have been some studies associated with unsteady compressibleflows over 2D wings as reviewed and extended by Bai and Wu.27The present authors28,29performed a numerical study on the compressible flows over a 60°swept delta wing undergoing pitching oscillation.They investigated the variations offlow patterns,vortex breakdown,and aerodynamic characteristics during a pitching cycle for various Mach numbers,mean angles of attack,pitching amplitudes and frequencies.In the present study,high subsonic and supersonicflows over a half-model 60°fixed and pitching delta wing are investigated experimentally,using surface pressure measurements.Also,a numerical simulation of theflow over the wing in the wind tunnel is performed for comparing and verifying the results.Distribution of the static pressure coefficient on the wing leeside and its variations with pitching cycles are extracted.Flow structure around the wing is demonstrated using the numerical simulation.

2.Experimental setup

2.1.Wind tunnel

All tests were conducted in a continuous suction-type wind tunnel with a rectangular section of 60 cm×60 cm.The turbulence intensity of theflow in the test section ranges from 0.4%to 1.4%depending on the freestream Mach number.The Reynolds number in the test section could be varied from 6.37×106to 7×107per meter.30The wind tunnel was trisonic,0.4≤Ma∞≤3.0 and the freestream Mach number was controlled by a variable nozzle and by throttling the engine.Theflow angle in the test section at a freestream Mach number of 2.0 was about 0.5°.A pitot tube was used to measure the freestream Mach number with a maximum error of 0.8%.The wind tunnel was calibrated for the ranges of Mach number.Theflow parameters,such asflow uniformity,flow angu-larity,and turbulence intensity were calculated and found to be within the acceptable range for this type of wind tunnel.There exist porous bleed holes on both the upper and lower walls of the test section that could stabilize and control wind tunnel shock and other reflected waves.The tunnel was of an indraft one and therefore the total pressure and total temperature in the test section were constant and atmospheric.

2.2.Model geometry

The delta wing model layout is illustrated in Fig.1.As thefigure shows,it is a half-wing which has leading-edge sweep angle of 60°.The upper surface is flat and the leading edge is sharp(15°angle made by the lower and upper surfaces at the leading edge)to minimize the effects of airfoil and leading edge shapes on theflow field.Wing thickness ratio is 0.058 based on the root chord length.A cylindrical shaft is attached to the wing at 2/3 root chord location which is connected to an oscillator system through the tunnelslide wallwindow.This mechanical-hydraulic oscillator system was capable of making pitch oscillations with a maximum frequency of 10 Hz and maximum amplitude of±7°.

2.3.Test procedure and location of sensors

Two sets of tests were carried out including static and dynamic(pitching)tests.Table 1 shows thatflow conditions were changed by freestream Mach numberMa∞,static angle of attack α,mean angle of attack α0,pitching amplitude ¯α,and frequencyf.Some conditions were repeated to assure the repeatability of the experiments.All data were acquired at a frequency of 2.0 kHz for 8 s at each mean angle of attack.Data acquisition time was sufficientfor stabilizing the flow and the sampling rate was sufficient for capturing the vortical flow phenomena.

A number of 69 pressure holes were fabricated on the upper surface of the wing.The holes were arranged infive spanwise sections located at 30%,45%,60%,75%,and 95%chordwise stations.Two sets of pressure transducers were applied to evaluating the instantaneous static pressure at the holes.Honeywell low-frequency differential sensors were used in static tests at all the pressure holes.Kulite high-frequency differential sensors were used in dynamic tests at 22 pressure holes.

Fig.2 shows the arrangement of pressure holes,their associated labels and locations of the pressure sensors.Kulite sensors were installed inside the model to minimize the time lag caused by the length of tubes,which is a critical issue in dynamic tests.Allsensorswere calibrated before the experiments.

3.Numerical methodology

The delta wing geometry in the tunnel test section was modeled for numerical simulation as in the experiment.Fig.3 shows the wing model in the tunnel and the computational grid in different views.The simulations were performed on an unstructured grid with triangular prisms in the boundary layer and tetrahedral elsewhere.The grid has approximately 3.2×106cells and was obtained after excessive simulation for grid independence study.A cylindrical zone was created around the wing whose axis is coincident with the wing pitch axis.The grid was refined within this cylinder to well capture the vortices above the wing.The cylindrical zone and the wing in it are rotated as a solid body.The cylinder surface is coincident with another cylindrical surface which isfixed and belongs to the rest of the domain(out of cylinder).These two surfaces have interface boundary condition.With this ‘‘sliding mesh” approach there is no need for time-consuming methods like spring mesh motion or remeshing.

Since the objective in this study is to accurately simulate theflow structure,grid study was performed by checking the convergence of the numeric values offlow field variables in severalflow field points,for several steady flow conditions.An example is shown in Table 2 for the average non-dimensional axial and tangential velocities(u/U∞,v/U∞)in a selected point near the vortex core.This point was located at a crossflow plane at 30%chordwise station,for theflow with Mach number of 2 and angle of attack of 20°.The grid has a first wall spacing ofy+≃1 which is appropriate for the turbulent model used.All surfaces of the wing and tunnel test section walls were specified as solid wall with no-slip boundary conditions.Inlet and outlet of the test section have pressure inlet and pressure outlet boundary conditions respectively.

Fig.1 Model of layout(left)and assembled(right).

Three-dimensional unsteady compressible Navier-Stokes equations are solved as the governing equations.Numericalfluxes for the convective terms are computed using the Roe’s scheme and the upwind MUSCL algorithm is applied to extending the spatial accuracy to 2nd order based on the primitive variables.The viscousfluxes are computed using the 2nd order central differencing.Theflow field is assumed to be fullyturbulent,and the two equation SSTk-ω turbulence model is applied.Different versions ofk-ω turbulent model have been found to be appropriate for capturing vortexflow over delta wings,by several researchers.28,29,31–33Schiavetta et al.31,32compared the Detached Eddy Simulation(DES)and Unsteady Reynolds-Averaged Navier-Stokes(URANS)turbulence modeling methods for the prediction of unsteady vorticalflows over delta wings.They concluded that URANS turbulence models are able to predict the dominant features of the lowfrequency phenomena present in the vortex system.An implicit dual-time algorithm is applied for the unsteady time integration.Density was calculated by ideal gas law and viscosity by Sutherland’s law.A valid CFD code was available for the researchers which had the above-mentioned capabilities.Several conditions of both static and dynamic experimental tests were selected to be simulated numerically.

Table 1 Experiment scenario.

Fig.2 Arrangement of pressure sensors.

Table 2 Axial and tangential velocity components at an arbitrary point for various grid sizes.

Fig.3 Computational grids.

4.Results and discussion

4.1.Numerical results

4.1.1.Static wing

3．不同病理分级NEN的SCGN、CgA阳性表达： G1、G2、G3级NEN中SCGN阳性表达率的差异有统计学意义(H=8.472，P=0.018，表2)，其中G1与G2级、G2与G3级NEN的SCGN阳性率差异无统计学意义，而G3级NEN的SCGN表达率显著低于G1级(秩均值：13.67比24.18)，差异具有统计学意义(Z=-2.506，P<0.017)。不同病理分级NEN的CgA表达差异无统计学意义。

Fig.4 shows numerical and experimental results obtained for the curves of static pressure coefficientCpspanwise distribution at several chordwise stations for four differentflow conditions.In general,good agreement is achieved between the numerical and experimental results,especially in the prediction of vortex core location over the wing.By increasing the angle of attack the suction predicted by numerical solution becomes slightly lower than experimental results.This difference becomes more significant when entering or getting close to the vortex breakdown region(Fig.4(b)).This difference could be expected because of the random nature of the breakdown region.Breakdown of primary vortex can be identified as sudden increase in pressure coefficient(suction drop)in chordwise direction.No sign of vortex breakdown is observed for supersonic conditions in Fig.4,even at high angles of attack.At supersonic freestream Mach numbers,the vortex core expands over the wing surface,thus a suction peak is not clearly seen,opposite to the subsonic conditions.28,29

Fig.5 shows the simulatedflow structure around the wing atMa∞=2.0，α =26°,among which Fig.5(a)shows the streamlines pattern at 30%chordwise station,Fig.5(b)local Mach number contour map and total pressure contour lines at 30%chordwise station,(Fig.5(c)pressure coefficient contour map at 90%chordwise station and a longitudinal plane,and(Fig.5(d),Mach number contour map at 90%chordwise station and a longitudinal plane.The presence of primary vortex in companion with an oblique shock wave above it is observed in thefigure.Increasing Mach number and angle of attack causes a conically supersonicflow above the vortex which has to be decelerated toward the tunnel side wall,so that the oblique shock appears.This shock decelerates theflow toward the wing and changes its direction.The vortex does not experience breakdown in this condition.Therefore,the high velocity-low pressure region of vortex core remains almost unchanged when moving downstream.There is a strong bow shock out of the wing which compresses theflow below it.

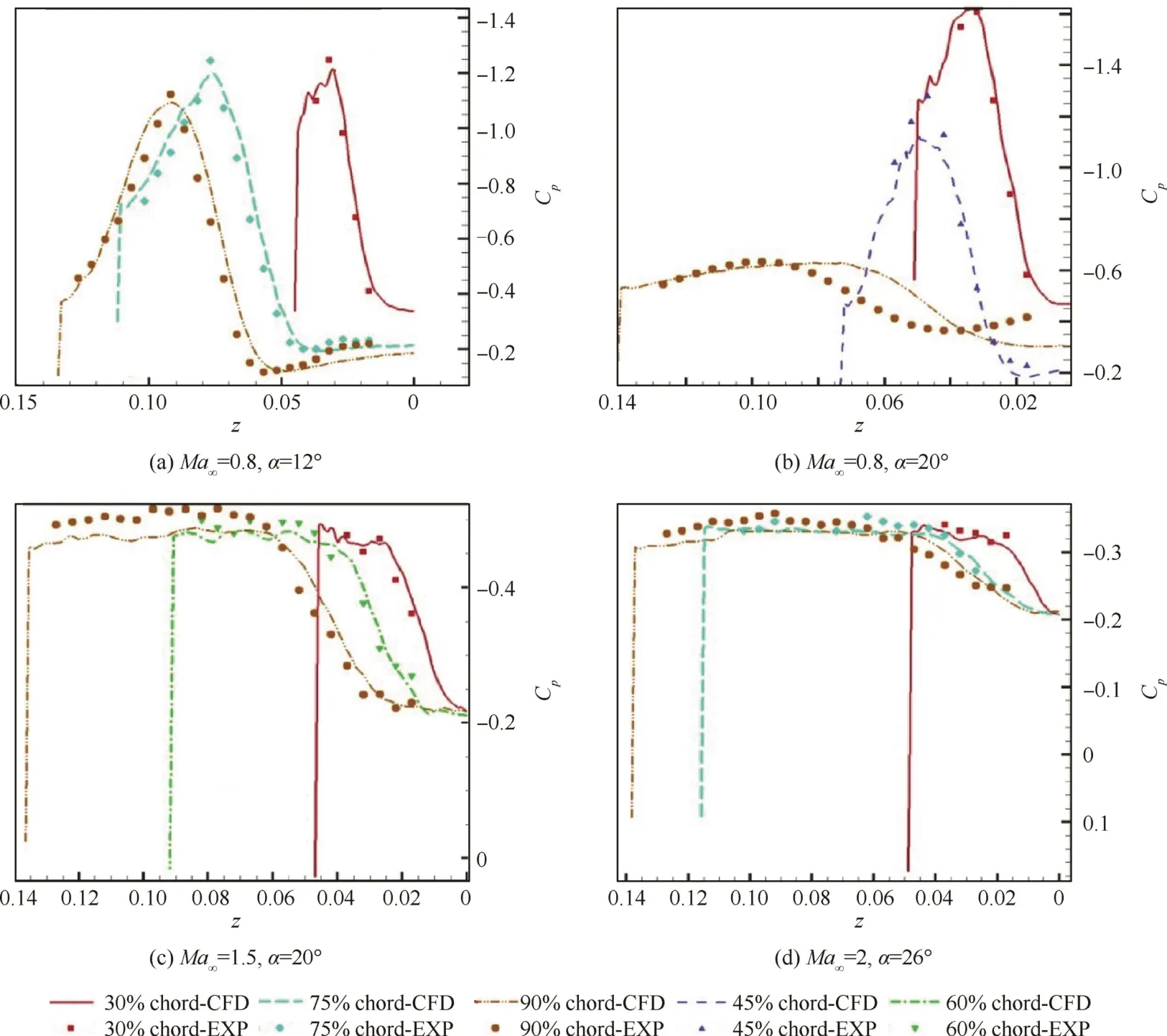
Fig.4 Comparison of numerical(CFD)and experimental(EXP)results for static pressure distributions along the spanwise direction(z)under various static conditions.

Fig.5 Flow structure around the wing at Ma∞ =2.0，α =26°.

4.1.2.Pitching wing

Fig.6 shows the hysteresis loops of static pressure coefficient in four sensor locations obtained by both simulations and experiments,at four different pitching oscillations.Labels associated with the holes were introduced in Fig.2.It is not expected that the numerical and experimental loops are completely coincident.However,it is seen that a good agreement exists in all curves,based on the order of magnitude,slope,and the behavior of the hysteresis loops.On condition that the sensor falls in the breakdown region(h65in Fig.6(a)and(b)),difference between the numerical and experimental results is more severe.This difference is expected because of the complex and random nature of the breakdown region.In general,it can be concluded that the static and dynamic results of the numerical simulations are reliable.

4.2.Experimental results

4.2.1.Static wing

Fig.7 shows the static pressure coefficient spanwise distribution curves measured by Honeywell sensors atfive chordwise sections,30%,45%,60%,75%,and 90%of wing root chord.Each picture shows the curves related to three Mach numbers,0.8,1.5,and 2 and a specific angle of attack.The angle of attack gradually increases from 0°to 26°in the sequence offigure parts.

As theflow moves downstream,the vortex core moves towards inboard.Until 20°angle of attack(Fig.7(e)),there is not a large difference between the pressure coefficient values at different sections.However,at α =20°a sudden drop in vortex suction is observed at 75%chordwise station and the suction peak disappears at 90%chordwise station.This phenomenon is obviously related to the vortex breakdown over the wing surface.The onset of breakdown starts at the trailing edge and moves upstream with increasing angle of attack.At supersonic Mach numbers,the effect of angle of attack on the pressure distribution is slighter in higher angles of attack and less variations in curves are seen.Increase of freestream Mach number makes adverse pressure gradient in the chordwise direction smaller and the location of breakdown moves downstream.Therefore,vortex breakdown is not observed at supersonic Mach numbers,even at the largest angle of attack.

4.2.2.Dynamic wing

Figs.8–14 show the hysteresis loops of static pressure coeffi-cient created by the pitching oscillation at the positions of Kulite sensors.They are located on the wing upper surface at 45%,60%,and 75%chordwise stations.In eachfigure,Mach number,mean angle of attack,and pitching amplitude have a specific value,and the effect of varying oscillation frequency(Figs.8,10 and 12)is shown.Any loop that does not intersect itself has counter-clockwise direction i.e.,the upstroke curve is below the downstroke curve.

Taking a glance at the curves and noting the mean values of pressure coefficients one can distinguish the presence of the vortex,like the static cases,as the spanwise minimum of mean pressure coefficients.The vortex core moves toward inboard when theflow moves downstream.It is more distinct andhas more suction forMa∞=0.8,relative toMa∞=2.ForMa∞=0.8 it can be seen that near the vortex core the slope of the curves increases,so does the amplitude of pressure coef-ficient variations in a pitching cycle.When getting far from the vortex core,these variations are alleviated,especially toward the wing root.Therefore,the difference between the maximum and minimum values which the sensor pressure coefficient reaches is reduced,so do the slope and width of the loops,which means a less phase difference between the upstroke and downstroke motions.

When all parameters arefixed except the pithing frequency,hysteresis loops are mostly different in their width so that their shapes or maximum and minimum values are almost the same.Increasing frequency has widened the loops atMa∞=2(Fig.12),but a regular trend is not seen forMa∞=0.8,although the effect of frequency is the same on all the loops under a specific condition.

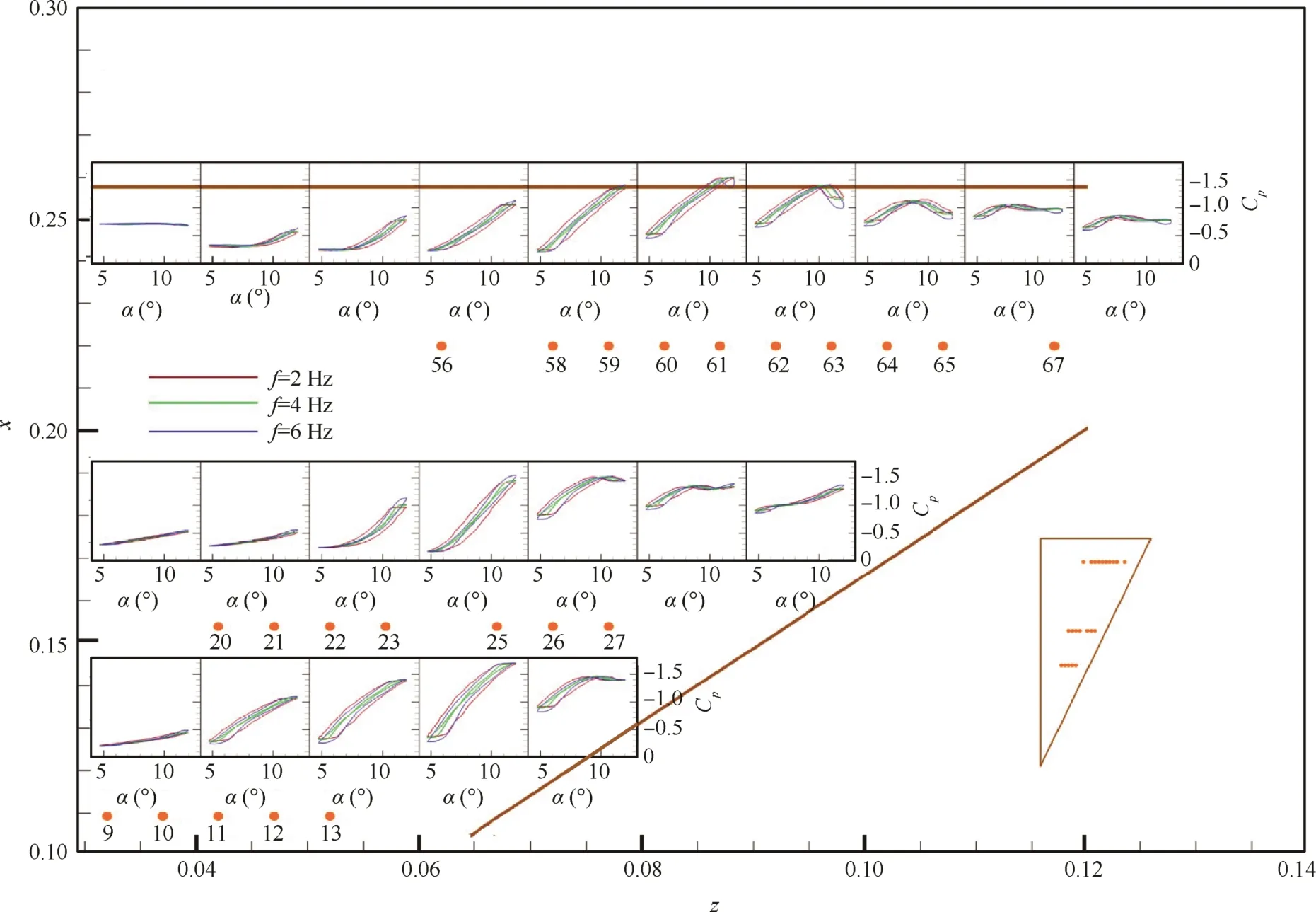
Fig.8 Pressure coefficients vs angle of attack hysteresis loops at Kulite sensor locations for Ma∞ =0.8，α0=8°，¯α =3.6°.

Fig.9 Pressure coefficients vs angle of attack hysteresis loops at Kulite sensor locations for Ma∞ =0.8，α0=8°，¯α =6.7°.

Fig.10 Pressure coefficients vs angle of attack hysteresis loops at Kulite sensor locations for Ma∞ =0.8，α0=12°，¯α =3.6°.

Fig.11 Pressure coefficients vs angle of attack hysteresis loops at Kulite sensor locations for Ma∞ =0.8，α0=12°，¯α =6.7°.

Fig.12 Pressure coefficients vs angle of attack hysteresis loops at Kulite sensor locations for Ma∞ =2，α0=12°，¯α =3.6°.

Vortex breakdown has a considerable effect on the loop shapes.In general,reduction of pressure coefficient with the increase of instantaneous angle of attack(upstroke motion)is approximately linear at low angles of attack and the curve slope is reduced at angles of attack larger than 12°(effect of increasing instantaneous angle of attack is reduced).However,vortex breakdown makes the curve slope change sign so that the pressure coefficient increases with increasing instantaneous angleofattack.Thisisobserved in somesensorsatMa∞=0.8.Under the conditions ofMa∞=0.8，α0=8°，¯α=3.6°(Fig.8),it seems that the onset of vortex breakdown in upstroke motion has occurred at trailing edge near the leading edge(holes 63 to 67).AtMa∞=0.8，α0=8°，¯α =6.7°(Fig.9),increase of oscillation amplitude has made the breakdown move upstream so that the whole of 90%chordwise station and a part of 60%chordwise section fall in breakdown region when reaching the largest angle of attack.Increasing oscillation amplitude naturally causes an increase in the range of pressure coefficient variations of a hysteresis loop in a particular point.Vortex breakdown almost neutralizes this effect.Comparing the conditionsMa∞=0.8，α0=12°，¯α =3.6°(Fig.10)andMa∞=0.8，α0=12°，¯α =6.7°(Fig.11),it is found that the increase in the range of pressure coefficient variations which is caused by increasing motion amplitude,is quite significant at sensors of 45%chordwise section and some sensors of 60%chordwise section which are closer to the wing root.These sensors fall outside of breakdown region.In the remaining sensors,increasing oscillation amplitude has much lower effect on the range of pressure coefficient variations.In Figs.9 and 11 it is seen that for ¯α =6.7°at high instantaneousanglesofattack where the vortex has burst,the phase difference between the upstroke and downstroke motions is very larger than lower instantaneous angles of attack in the same cycle.For those sensors which lie in the burst region,the hysteresis loops demonstrate high-frequency fluctuations and the loops ofadjacent sensors have major differences.These are caused by high intensity turbulence and random variations in vortex breakdown region.

In some cases,the 8-shape phenomenon occurs in the hysteresis loops,which means the intersection of a loop by itself.This self-intersection implies a sign change in phase difference which means that the lead and lag of coefficients have been exchanged between the upstroke and downstroke motions.This phenomenon is observed in most cases where breakdown has occurred and intersection of the curve by itself can occur several times.However,8-shape is seen in some cases where vortex breakdown has not occurred.AtMa∞=2，α0=20°，¯α =6.7°multiple self-intersections are seen in many sensors(Fig.13).

The integrated effect of the surface pressure distribution can be interpreted by aerodynamics coefficients.Because of the configuration used in the present experimental setup,it was not possible to measure the aerodynamic loads using a balance.However,they can be calculated by numerical simulation.An example is shown in Fig.15 for lift coefficientCLhysteresis loops for two different conditionsMa∞=0.8，α0=20°，¯α=3.6°，f=2 Hz andMa∞=2，α0=20°，¯α =6.7°，f=2 Hz.Wider loop forMa∞=0.8 means larger phase difference between upstrokeand downstrokemotions.A narrow 8-shape is observed forMa∞=2.

Fig.14 Pressure coefficients vs angle of attack hysteresis loops at Kulite sensor locations for Ma∞ =2，α0=20°，¯α =6.7°.

Fig.15 Hysteresis loops of lift coefficients for two flow conditions obtained by numerical simulation.

5.Conclusions

Numerical and experimental investigations of the compressibleflows over a 60°delta wing were performed for static and pitching oscillation modes.Using wind tunnel static tests the spanwise distributions of pressure coefficient over the wing surface were obtained at multiple chordwise sections.Using dynamic tests,the hysteresis loops of pressure coefficient versus angle of attack were obtained at the positions of high frequency sensors.Both typesofresultswere used for comparison with numerical simulations and the results were verified.Flow structures around the wing were also demonstrated using numerical simulations.Here are the main points concluded:

(1)Results of static tests show that with the increase of angle of attack,the vortex becomes stronger and its core moves toward inboard and farther from the surface.As theflow moves downstream,the core moves toward the wing inboard.By increasing Mach number the pressure coefficient increases.Vortex breakdown in subsonicflow is characterized by a sudden drop in suction peak relative to the upstream points.At supersonic Mach numbers,the effect of angle of attack on the pressure distribution is reduced at high angles of attack.

(2)Results of dynamic tests show that at Mach number of 0.8,the slope of hysteresis loops and the range of variations of pressure coefficient in a pitching cycle are larger at positions closer to the vortex core.At Mach number of 2,increasing frequency widens the loops,but a regular trend of frequency effect is not observed at Mach number of 0.8.Vortex breakdown causes the curve slope to change sign and pressure coefficient to increase with increasing instantaneous angle of attack.Increasing oscillation amplitude causes the increase in the range of pressure coefficient variation in a cycle,although the vortex breakdown neutralizes this effect.In most cases where vortex breakdown exists and some cases where it does not,8-shape phenomenon is observed in hysteresis loops as self-intersection of the loop by one time or more.

1.Gursul I.Recent developments in delta wing aerodynamics.Aeronautical Journal2004;108(1087):437–52.

2.Gursul I.Review of unsteady vortexflows over slender delta wings.Journal of Aircraft2005;42(2):299–319.

3.Rockwell D.Three-dimensionalflow structure on delta wings at high angle-of-attack:Experimentalconceptsissues.Reston:AIAA;1993.Report No.:AIAA-1993-0550.

4.Visbal MR.Computational and physical aspects of vortex breakdown on delta wings.Reston:AIAA;1993.Report No.:AIAA-1995-0585.

5.Maltby RL,Engler PB,Keating RFA.Some exploratory measurements of leading-edge vortex positions on a delta wing oscillating in heave.Aeronauticalresearchcouncil,researchandmemorandum.1963.

6.Lambourne NC,Bryer DW,Maybrey JFM.The behavior of the leading-edgevorticesoveradeltawingfollowingasuddenchangeof incidence.Aeronauticalresearchcouncil,researchandmemorandum.1963.

7.Gad-el-Hak M,Ho CM.Pitching delta wing.AIAA Journal1985;23(11):1660–5.

8.Gursul I,Yang H.Onfluctuations of vortex breakdown location.Physics of Fluids1995;7(1):229–31.

9.Gursul I,Ho CM.Vortex breakdown over delta wings in unsteady freestream.AIAA Journal1994;32(2):433–6.

10.Visbal MR,Gordnier RE.Pitch rate and pitch-axis location effects on vortex breakdown onset.Journal of Aircraft1995;32(5):929–35.

11.Atta R,Rockwell D.Hysteresis of vortex development and breakdown on an oscillating delta wing.AIAA Journal1987;25(11):1512–3.

12.LeMay SP,Batill SM,Nelson RC.Vortex dynamics on a pitching delta wing.Journal of Aircraft1990;27(2):131–8.

13.Magness C,Robinson O,Rockwell D.Instantaneous topology of the unsteady leading edge vortex at high angle of attack.AIAA Journal1993;31(8):1384–91.

14.Lin JC,Rockwell D.Transient structure of vortex breakdown on a delta wing.AIAA Journal1995;33(1):6–12.

15.Gursul I.Proposed mechanism for time lag of vortex breakdown location in unsteadyflows.Journal of Aircraft2000;37(4):733-6.

16.Yavuz MM,Elkhoury M,Rockwell D.Near-surface topology andflow structure on a delta wing.AIAA Journal2004;42(2):332–40.

17.Goruney T,Rockwell D.Effect of pitch rate on near-surface topology on a delta wing.AIAA Journal2010;48(6):1207-20.

18.Liu J,Sun HS,Liu ZT,Xiao ZX.Numerical investigation of unsteady vortex breakdown pastdouble-delta wing.Chinese Journal of Aeronautics2014;27(3):521-30.

19.Stanbrook A,Squire LC.Possible types offlow at swept leading edges.Aeronautical Quarterly1964;15(2):72-8.

20.Miller DS,Wood RM.Leesideflows over delta wings at supersonic speeds.Journal of Aircraft1984;21(9):680-6.

21.Szodruch JG,Peake DJ.Leewardflow over delta wings at supersonic speeds.Washington,D.C.:NASA;1980.Report No.:NASA-TM-81187.

22.SeshadriSN,NarayanKY.Possibletypesofflowonlee-surfaceofdelta wingsatsupersonicspeeds.AeronauticalJournal1988;92(915):185-99.

23.Brodetsky MD,Shevchenco AM.Some features of a separatedflow and supersonic vortex structure at the leeside of a delta wing.Proceeding of the IUTAM symp.on separatedflows and jets.1990.p.341-4.

24.Brodetsky MD,Krause E,Nikiforov SB,Pavlov AA,Kharitonov AM,Shevchenco AM.Evolution of vortex structures on leeward side of a delta wing.Journal of Applied Mechanics and Technical Physics2001;42(2):243-54.

25.Imai G,Fujii K,Oyama A.Computational analyses of supersonicflows over a delta wing at high angles of attack.25th international congress of the aeronautical sciences(ICAS),Hamburg,Germany.2006.

26.Oyama A,Ito M,Imai G,Tsutsumi S,Amitani N,Fujii K.Mach number effect onflow field over a delta wing in supersonic region.46th AIAA aerospace sciences meeting and exhibit,Reno,Nevada,USA,2008.

27.Bai CY,Wu ZN.Hypersonic startingflow at high angle of attack.Chinese Journal of Aeronautics2016;29(2):297-304.

28.Hadidoolabi M,Ansarian H.Computational Investigation of theflow structure over a pitching delta wing at supersonic speeds.Proceedings of the Institution of Mechanical Engineers,Part G:Journal of Aerospace Engineering2016;230(7):1334-47.

29.Hadidoolabi M,Ansarian H.A numerical analysis of theflow pattern and vortex breakdown over a pitching delta wing at supersonic speeds.Journal of Applied Mechanics and Technical Physics2017;58(3):392-401.

30.Soltani MR,Sepahi-Younsi J.Buzz cycle description in an axisymmetricmixed-compression airintake.AIAAJournal2016;54(3):1036-49.

31.Schiavetta LA,Boelens OJ,Fritz W.Analysis of transonicflow on a slender delta wing using CFD.24th applied aerodynamics conference,San Francisco,California,USA,2006.

32.Schiavetta LA,Badcock KJ,Cummings RM.Comparison of DES and URANS for unsteady vorticalflows over delta wings.46th AIAA aerospace sciences meeting and exhibit,Reno,Nevada,USA,2007.

33.Younis Y,Bibi A,Haque AU,Khushnood S.Vorticalflow topology on windward and leeward side of delta wing at supersonic speed.Journal of Applied Fluid Mechanics2009;2(2):13-21.