A Bayesian approach for integrating multilevel priors and data for aerospace system reliability assessment

Jian GUO,Zhaojun LI,Thomas KEYSER

Department of Industrial Engineering and Engineering Management,Western New England University,Springfield,MA 01119,USA

1.Introduction

In the product development process for aerospace systems,system-level reliability testing is very costly and can end up with very limited test data.Product experts may have valuable reliability knowledge based on understanding of adopted new technologies,complexity of a new product,manufacturability,and other factors which have impacts on product reliability.Integrating limited testing data with expert reliability knowledge can significantly improve aerospace system reliability estimation with significant potential cost savings on system-level reliability testing.When there exist different levels of reliability prior information and testing data at system and/or subsystem levels,integrating such multilevel information can be challenging.Bayesian inference is one of the most viable methods to quantify expert reliability knowledge through appropriate prior distribution elicitation.In addition,Bayesian methods are capable of dealing with limited aerospace testing data.1Recently,Bayesian reliability inference has received increasing applications and acceptance for reliability estimation when there exists limited data.2

For a complex aerospace system,system-or higher-level module reliability is dependent on subsystem-or lower-level module reliability performance.Thus,system reliability can be assessed based on lower-level module reliability performance.Inversely,system reliability information can be used for subsystem-and module-level reliability inferences and updates.In this research,we investigate four common scenarios based on the availability of different levels of prior reliability information and data shown in Fig.1.These four scenarios are(A)using the subsystem data and prior;(B)using the subsystem prior and data as well as the system prior;(C)using the subsystem prior as well as the system prior and data;and(D)using both system and subsystem data and priors.To obtain the posterior system reliability inference for each of these four scenarios,specific Bayesian methods are suggested in order to better deal with the unique data and priors available.

When only a single level of data and prior information is available,Bayesian reliability inference for a unit,e.g.,a component,subsystem,or system,can proceed by following the standard Bayesian procedure.1,2For system reliability analysis using the prior and data of components/subsystems,extensive research has been conducted under the Bayesian inference framework.Springer and Thompson3,4developed the Bayesian reliability confidence intervals of a product withNindependent subsystems using the beta prior and binary test data.Tang et al.5proposed a Bayesian method along with the moment function to estimate system reliability with component binary test data and Beta priors for series,parallel,and mixed systems.Singh et al.6applied the Bayesian approach in component-based software development by including a system’s internal structure.Assuming exponentially-distributed failure time,Mastran7and Mastran and Singpurwalla8applied Bayesian methods for reliability assessment of a coherent system using binary test data and priors from both components and the system.Martz et al.9,10studied the overall reliability of an air-to-air heat-seeking missile system using a two-stage Bayesian procedure.

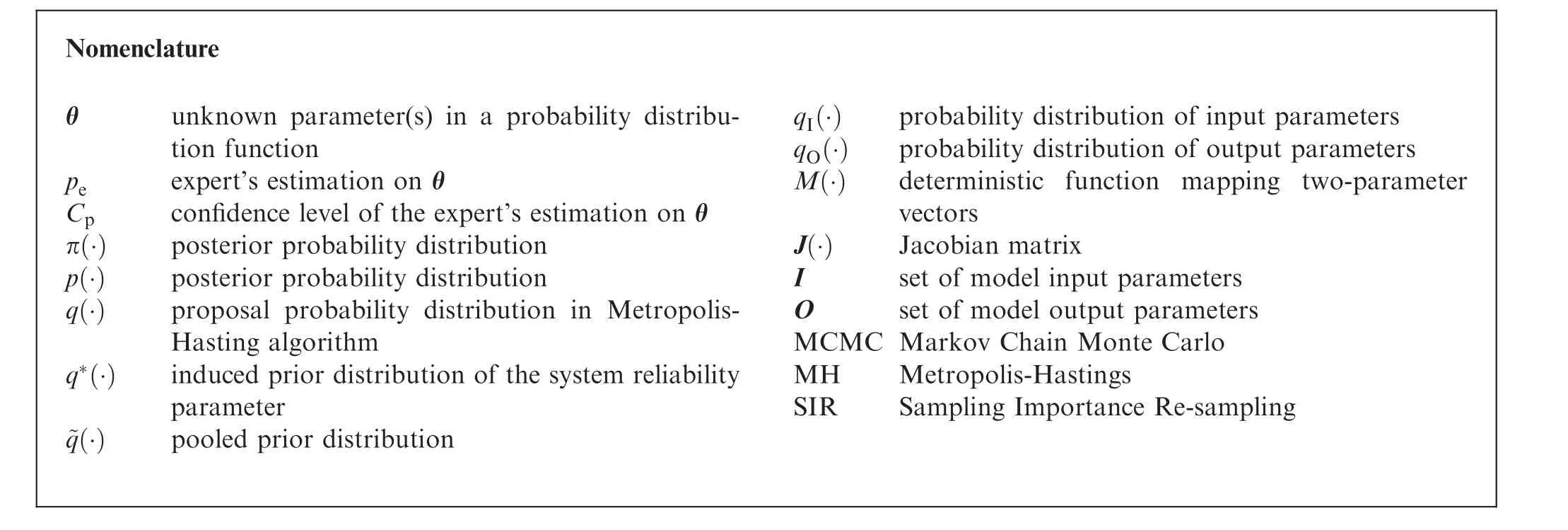
Nomenclature θ unknown parameter(s)in a probability distribution function pe expert’s estimation on θ Cp confidence level of the expert’s estimation on θ π（·） posterior probability distribution p（·） posterior probability distribution q（·） proposal probability distribution in Metropolis-Hasting algorithm q*（·） induced prior distribution of the system reliability parameter~q（·） pooled prior distribution qI（·） probability distribution of input parameters qO（·） probability distribution of output parameters M（·） deterministicfunctionmappingtwo-parameter vectors J（·） Jacobian matrix I set of model input parameters O set of model output parameters MCMC Markov Chain Monte Carlo MH Metropolis-Hastings SIR Sampling Importance Re-sampling

Fig.1 Various scenarios for aerospace system and subsystem reliability assessment.

To aggregate the multilevel prior and data from both a system and its subsystems,a Natural-Conjugate(NC)method proposed by Winkler11was used to average theinduced priorand thenative prior,in which the induced prior is derived based on the system structure and thenative prioris the existing system-level prior.In addition,prior knowledge can be incorporated through a hierarchical model where the parameters of reliability distributions are assigned to follow certain distributions or dynamic functions to resolve estimation aggregation.Hamada et al.12combined multilevel failure information in a fault tree by multiplying the high-level event probability in the posterior distribution,which assigned equal weights to the native and induced beta prior distributions.Bier13systematically discussed the consistency between the results of aggregated system-level reliability and disaggregated component-level reliability analysis of the same system using Bayesian estimation,and observed the two avenues rarely concur for complex systems.In order to address the consistency issue in Ref.13,Johnson et al.14proposed a Bayesian hierarchical model to incorporate reliability point estimation from experts with binary test data.Wilson et al.15summarized Bayesian hierarchical methods for binary,lifetime,and degradation data.The Bayesian melding method,which was initially proposed by Poole and Raftery16to evaluate the population evolution of bow-head whales,has also been applied to integrate subsystem-level priors with system priors for system posterior reliability inference.For example,Reese et al.17and Guo and Wilson18studied how to integrate heterogeneous multilevel information in assessment of system reliability using the Bayesian melding method.However,very little literature exists pertaining to using system-level reliability information to update subsystem-level posterior reliability under various scenarios in terms of availability of multilevel prior and data.This is a unique aspect of this research.

Computational challenges of Bayesian inference are often related to complex integrations for computing and evaluating posterior distributions,marginal distributions,and posteriorbased predictions.For cases with non-conjugate priors and high-dimensional parameter space,numerical methods such as Approximate Bayesian Computation(ABC),19importance sampling,iterative quadrature,Laplace approximation,Monte Carlo Markov Chain(MCMC),and variational Bayes have been used.For many high-dimensional problems,MCMC methods could be the only choices.20MCMC methods are a practical set of computational tools which exploit the probabilistic properties of integrands rather than the analytic properties.21In Bayesian reliability analysis,MCMC methods are capable of dealing with complex parametrization and likelihood functions. Specifically, Gibbs sampling22and Metropolis-Hastings(MH)23,24algorithms are the two most popular computational methods for Bayesian inference.Gibbs sampling is an iterative sampling technique overcoming the dimensionality issue when full conditionals are available.25When parameter spaces have different dimensionalities and conditional distributions are not in closed forms,the MH algorithm,a more generic version of Gibbs sampling,becomes necessary.However,for the proposed Bayesian system reliability analysis using the Bayesian melding method in which component and system priors as well as the induced system prior have been sampled,the traditional MCMC method becomes ineffi-cient due to repeated likelihood function evaluations in the MCMC sampling process.Such issues become more serious when a large number of sampling data is needed and the complicated posterior distribution consists of multiple-level priors and complex likelihood functions.Thus,the Sampling Importance Re-sampling(SIR)method with less algorithm complexity is suggested in the proposed Bayesian melding method for aerospace systems reliability assessment.

The remainder of the paper is organized as follows.Section 2 presents the basic procedure of Bayesian methods in reliability applications with an overview of the three key elements in Bayesian statistics inference,i.e.,prior elicitation π（θ）,sampling modely（θ）,and posterior inferencep（θ）.Section 3 investigates different ways of using Bayesian methods for assessing system reliability based on the availability of system and subsystem prior distributions and data(Fig.1).An aerospace system is presented as a case study to demonstrate the applications of the proposed methods in Section 4.Section 5 draws conclusions and discusses future research work.

2.Bayesian procedure for reliability assessment

The three key elements in Bayesian statistics inference are prior elicitation,sampling model,and posterior computation.Prior information reflects existing knowledge about the unknown parameter θ before any data is collected.Sampling models describe the frequency variation over the observed data,through which the test data is described in likelihood functions.The posterior distribution can then be evaluated through integrating the prior information and the likelihood functions.When complex priors and sampling models are used,deterministic closed forms of posterior distributions usually do not exist.In such cases,simulation techniques such as MCMC can be used to assess posterior distributions and proceed with further Bayesian inference and Bayesian predictive inferences.Simulations are also used to resolve computational difficulties in high-dimensional parameterization cases to avoid the ‘‘curse of dimensionality”.

2.1.Prior elicitation,sampling model,and posterior inference

Bayesian inference often starts with eliciting a prior distribution to appropriately model existing knowledge,previous experiences,and subjective beliefs through a probability statement about the unknown parameter θ.In reliability engineering,expert engineering judgment can provide important references for modeling the reliability of a system.26Expert judgment should follow the law of probability,27i.e.,estimations on the key parameters of a prior distribution need to come with a corresponding probability.Expert engineers can either provide parameter estimations of prior distributions of interest directly or present the estimates of certain key parameters in the prior such as a lower percentile value and an associated confidence level.When conjugate prior distributions are applicable,the posterior distributions are within the same family of probability distributions.Hamada et al.2summarized various types of reliability data,sampling distributions,and prior distributions.For binary data(pass/-fail),the binomial sampling model with its conjugate beta distribution has been widely used.Weiler28investigated methods of estimating the parameters of a beta prior for various types of historical observations including the expectation of the rateE（θ）,the probability ofP（θ ＞ θ0）,and the numbers of success events in pastNtrials.Specifically,a beta distribution is defined as

where θ,the parameter of interest,is the probability that an experiment passes the pass/fail test and Γ（·）is the gamma function.Parametersaandbare the shape parameters of the beta distribution,which are usually called super parameters in Bayesian inferences.These super parameters can be determined based on expert estimation about θ,for example,the estimated mode or mean of θ and a corresponding confidence level of the mode or mean estimate based on historical pass/fail test outcomes.

In addition to using point estimates for θ,an interval estimate for θ with a confidence level can also be used to determine the prior distribution.29The confidence level or weight can be defined in a relative scale using natural numbers.For instance,a value of confidence level of 20 indicates a high con-fidence level,while a confidence level of 5 indicates a low con-fidence level for the associated estimates,e.g.,the mode or mean for θ.Denote expert estimation on the mode of θ and the confidence level aspeandCp,respectively.Thenaandbcan beparameterized asCppe+1 andCp（1-pe）+1,respectively.14

When other types of test data exist,probability models such as Poisson,exponential,and Weibull models can also be used for prior distribution modeling.Various types of prior and posterior distributions are suggested in the literature.2Taking the Poisson distribution with counting failure data as an example,parameterλ.rivalrateλin Poisson distributionY～ Poisson λtmodels failure counting data at a time point oft,whereYis the total number of occurrences.The conjugate gamma prior distribution Gamma（α，β）with the shape parameter α and the scale parameter β for the Poisson sampling model can be employed to obtain a closed-form posterior distribution for parameter λ.

Posterior distribution inference integrates prior information and observed data through a likelihood function.With a conjugate prior distribution,the posterior distribution can be easily evaluated.Using the previous parameterization notationspeandCpfor a beta prior distribution,the posterior distribution with binary test data is

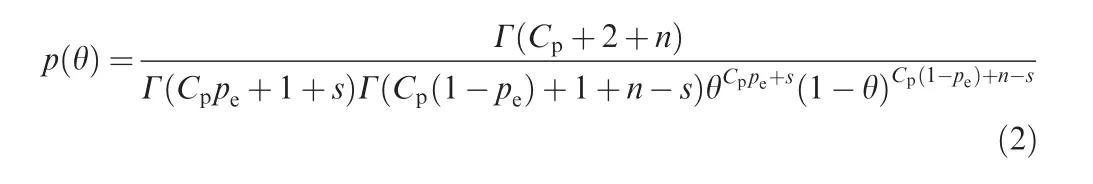
wheresandnare the numbers of passes and total tests,respectively.

2.2.Bayesian posterior inference using simulation

Applications of Bayesian inference in aerospace system reliability analysis aim to estimate unknown reliability parameters,determine marginal effects,and predict future failures or success probabilities.Such Bayesian statistical inferences can be computationally intensive due to the non-conjugate prior specification and high-dimensional parameterization.Often simulation techniques will become imperative.Among various simulation techniques,MCMC methods have been widely used to evaluate the posterior reliability of complex systems.Evans and Swartz20believed that MCMC methods are the only choices for high-dimensional problems.MCMC methods aim to evaluate essential statistics such as the mean,percentiles,and higher-order moments of the posterior distribution,which usually does not have a closed-form solution.Such approximation and simulation methods of evaluating the posterior distribution can be realized through generating a sequence of samples ｛θ1，θ2，...，θs｝ so that the following equation holds under the ergodic theory with a large number of simulation runs:

whereg（θ）is any function of interest of the unknown parameter θ,which could be a high-dimensional vector.The target distribution functionp（θ）is the posterior distribution in Bayesian inference.Liang et al.25summarized various MCMC algorithms,among which Gibbs sampling22and Metropolis-Hastings23,24algorithms are the most commonly utilized for Bayesian inference.In order to obtain the posterior distribution of the unknown parameter θ,the Metropolis-Hastings method proposes a new value θ*around the current value θsusing a proposal distribution and determines whether to assign θ*as the next value of θs+1through an acceptance ratioras follows:

The proposal distributionq（·）from which new samples are generated is critical for rapid convergence of the Metropolis-Hastings(MH)algorithm.Ifp（·）can be sampled directly,the fastest-converging proposal distribution would be the target distribution,30where the acceptance ratio equals one.Chib and Greenberg31proposed a solution to specify the proposal distribution for a given form ofp（·）.If the target distributionp（·）can be written asp（·）∝ φ（·）h（·）,whereh（·）can be sampled and φ（·）is uniformly bounded,it is feasible to seth（·）as the proposal distribution.Since the posterior distribution is the product of the prior distribution and a sampling distribution which is always less than 1,the prior distribution π（·）becomes a good candidate for the proposal distribution.The method of using the prior distribution as the proposal distribution in the MH algorithm is investigated in this research.

3.System reliability assessment using multilevel information

System reliability depends on reliability performances of subsystems as well as complex interactions within a given system structure.This section investigates different ways of integrating multilevel data and priors using specific Bayesian inference techniques.

3.1.System reliability assessment based on a single level of prior and data

When only a single level of subsystem priors and data is available,system reliability can be evaluated using the ‘‘bottomtop”approach based on the system structure.Fig.2 shows an example of a mixed system consisting of both parallel and series subsystems.The success rate or reliability of an individual subsystem is θ under the Bernoulli experimentation.The system reliability can be expressed as follows:wheregindicates the number of subsystems connected in series,hindicates the number of subsystems connected in parallel,Ljis the number of sub-subsystems/components in thejth parallel subsystem,θiis the reliability of theith subsystem in series,and θkis the reliability of thekth sub-subsystem in thejth parallel subsystem.

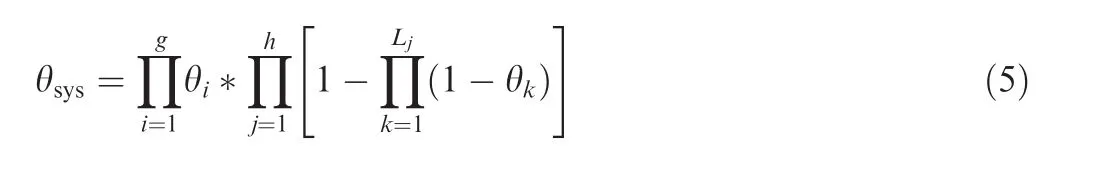
Using the mixed system in Fig.2,with the binary test data and beta distribution assumptions,the posterior distributions of θ for each subsystem can be evaluated by integrating subsystem-levelpriors and testdata information.The system-level posterior can then be evaluated using the reliability block diagram analysis and system structure.When the prior elicitation is realized using expert inputs forCpiandpei,the closed-form subsystem posterior reliability can be evaluated using Eq.(2).Since there is no closed-form probability distribution for the system-level posterior distribution,Monte Carlo(MC)simulations at the subsystem level can be aggregated for system-level posterior reliability inferences.When non-conjugate priors are used,no closed-form posterior probability distributions exist for subsystem-level reliability,and MCMC becomes a viable method for subsystem and system posterior reliability inferences.

Fig.2 Example of a mixed system with parallel and series subsystems.

3.2.System reliability assessment based on multiple levels of prior and data

System reliability assessment based on the system structure can effectively deal with the situation when only subsystem data and priors are available.When multilevel data and priors from subsystems and the system are available,Bayesian melding methods for integrating such multilevel information are investigated in this section.

3.2.1.Bayesian melding method for integrating multilevel priorsIn the literature,Martz et al.9,10and Hamada et al.12integrated multilevel prior information by assigning equal weights to the native and induced system priors.However,using system reliability information to update subsystem-level posterior distributions has not been well investigated.Instead of averaging multilevel prior distributions using equal weights,the Bayesian melding method derives the induced prior distribution via a deterministic model and integrates the induced prior with the native prior using mathematical pooling algorithms.

The Bayesian melding method was developed based on Bayesian synthesis32that is used to simulate the population evolution process of bowhead whales.In Bayesian synthesis,the marginal posterior distribution of input parameters is defined aspI（I）=pI|O（I|O=M（I））,whereM（·）is a deterministic function,and I and O stand for sets of input and output parameters,respectively.However,Wolpert33proved that Bayesian synthesis has the Borel paradox problem since posterior distribution simulation depends on the selection of the deterministic functionM（·）.The Bayesian melding method eliminates this deficiency by reformulating via a standard Bayesian procedure.The induced prior distribution of the output,denoted byq*I（O）,integrates information from input probability distributionsqI（I）and the deterministic functionM（I）,which means thatq*I（O）=q*I（M-1（O））|J（O）|,givenM（·）is invertible.The pooled distribution of the output,~qO（·）,can be derived by pooling the induced prior,q*I（·）,and the native prior,qO（·）.The two main pooling methodologies are the linear pooling and logarithm pooling methods,which were initially used to integrate multiple expert opinions.Genest et al.34proved that the logarithmic pooling operator is the only pooling operator that can meet the requirement of external Bayes property,i.e.,leading to the same posterior probability distribution regardless of the order of updating priorsfirst and then combining them,or combining priorsfirst and then updating them.The pooled prior distribution of the output under the logarithm pooling algorithm is

An updated subsystem prior can be evaluated based on~qO（O）andM（·）,i.e.,~qO（O）is converted to I space through O=M（I）.Moreover,an updated system prior reliability can also be obtained from the updated subsystem priors through the system configuration.Assume thatC1is a hypercube in a higher-dimensional space andC2is a hypercube in a lowerdimensional space mapped fromC1through a convertible deterministic functionM（·）.C3is a hypercube in the same dimensional space as that ofC2viaC3=M-1（C2）.C1,C2,andC3are shown in Fig.3.In addition,with the assumption that I∈C1,O=M（I）∈C2,andP（C2）=P（C3）,whereP（·）denotes any probability distribution.Due to the definitions ofC2andC3,qI（C3）=q*I（C2）.Eqs.(7)and(8)show the derivation of the pooled distribution of the input,where the inverse function,M-1（·）,is not involved.Thus Eq.(8)also applies to cases when the deterministic functionM（·）is nonconvertible.It is observed from Eq.(8)that the pooled input prior distribution~qI（I）is the original prior weighted by the ratio of two probability densities ofqO（M（I））andq*I（M（I））,evaluated atM（I）.

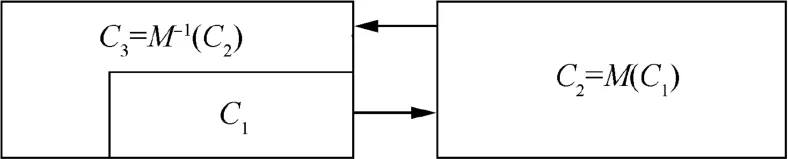
Fig.3 Schematic for prior integration and allocation using Bayesian melding.

3.2.2.Simulation algorithms for posterior inference underBayesian melding

According to the standard Bayesian inference,the posterior can be made inferred with the prior and corresponding data.Induced and pooled system priors are often very complex and do not have a closed form in most cases.As a result,simulation methods such as MCMC methods and importance sampling methods need to be deployed to obtain their posteriors.Reese et al.17and Guo and Wilson18applied MCMC in Bayesian melding computation.Taddy et al.35recommended SamplingImportanceRe-sampling(SIR),which was initially developed by Rubin36for generating samples of induced and pooled prior distributions.The SIR method can simulate and evaluate both subsystem and system posteriors more efficiently using samples from subsystem priors,induced system prior,and pooled system prior distributions.The computation complexity of MCMC methods in this case isO（nlgn）37which is larger thanO（n）of using the SIR method,whereO（·）describes the limiting behavior of a function when the argument tends towards a particular value or infinity.Formally the SIR standard procedure can be described as follows:

提升煤矿运输的稳定性与安全性，能够确保煤矿作业有效进行，在煤矿作业效率得到保障以后，整个采矿工程才能顺利推进。在煤矿运输上应用机电一体化数控技术以后，通常反映在煤矿提升设备与带式传输设备等方面，对矿井提升设备来说，可以让煤矿作业效率得到提升，满足煤矿作业的提升要求。[2]现在通过实现内装式提升设备的一体化，也是这项技术的优势之一，不仅可以充分简化设备结构，也连接了滚筒和驱动，大大提升了机械设备的安全性。对带式传输设备来说，在现阶段煤矿作业中应用比较多，自动化水平也很高，能够保证煤矿开采的稳定、高效进行，让煤矿作业效率的提升有了可靠的技术支持。

(1)Generate θ from qI（θ）and evaluate θsys=M（θ）to obtain θsys.Assume that subsystems in a complex system are independent and all follow beta probability distributions.The joint probability distribution of the subsystem reliability is:

wherenis the number of subsystems in the system.aiandbiare the super parameters of beta distribution of unknown parameter θiof each subsystemi,which can be evaluated asCpi×peiandCpi× （1-pei）,respectively,according to Eq.(2).

(2)Evaluate q*I（θsys）using the nonparametric density estimation,i.e.,q*I（θsys）=q*I（M（θ））.

(3)Calculate the importance weights as

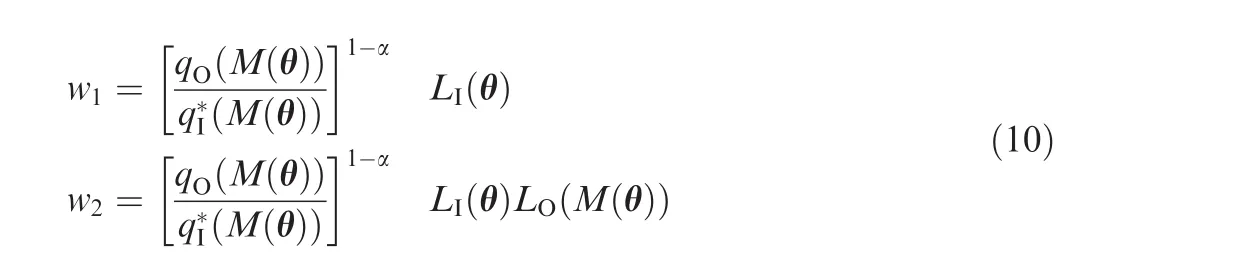
wherew1andw2are the weights for posteriors using the subsystem data and both the subsystem and system data,respectively,whileLI（θ）andLO（M（θ））are the likelihood functions of the subsystems and system,respectively.

(4)The posterior distribution of θ is the product of the prior distribution of θ and the importance weight w1or w2as follows:

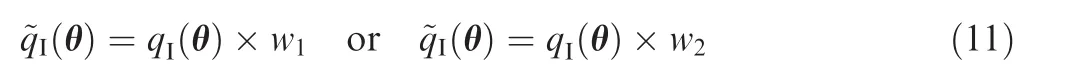
The SIR algorithm may not work well due to the issue of centered large importance weights which occurs occasionally.In other words,a small number of large importance weights can dominate the re-sampling process.Raftery and Bao38discussed the centered sampling issue in sampling HIV population via SIR.In order to address this issue,an adaptive importance sampling scheme has been suggested in the literature.Liang39extended the pruned-enriched Rosenbluth method by imposing upper bounds on weights to limit the usage of certain samples.The enrichment method distributes samples with extremely large weights evenly to samples with smaller weights.By splitting large weights into smaller ones,a wider range of samples is explored,and the importance sampling estimator is still unbiased.In the proposed Bayesian melding method for system reliability assessment using the SIR method,weights are functions of the induced system prior,native prior,and likelihood functions of both the system and subsystems,as shown in Eq.(10).One key parameter of the adaptive enriched scheme is to set the threshold weight,which needs to be pre-determined.Yuan and Druzdzel40proposed a cumulative weight method to initialize threshold weights.More specifically,

(1)Generate weight samples using Eq.(10);

(3)Sort these weights ascendingly and assign a threshold weightwhere γ is denoted as the threshold percentage;

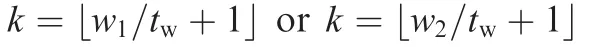
(5)Repeat Steps 1–4 until the variance of weights reaches the pre-determined value.This research uses standard deviation as the pre-determined threshold value.

4.A case study of Bayesian melding method for an aerospace system reliability assessment

This section applies the proposed methods for an aerospace system reliability assessment under different Bayesian information integration methods.System reliability assessment outcomes are compared under four major scenarios based on the availability of prior information and test data.

Fig.4 An aerospace system reliability block diagram(RBD).41

4.1.Background

The case study addresses a critical piece of an aerospace system whose reliability block diagram is shown in Fig.4.41Subsystems 1,2,and 5 are in a series structure,while subsystems 4a and 4b are in a parallel structure.It is very costly to implement testing for reliability demonstration,especially at the system level.Only subsystem-level test results and limited systemlevel historical testing data in terms of either pass or fail are available.The objective is to estimate the parameter,θsys,of the system reliability by utilizing limited binary testing data and expert prior knowledge.Table 1 shows subsystems test results,where ‘‘P”, ‘‘F”,and ‘‘NT”stand for pass,fail,and not-tested,respectively.The historical statistical data of a system-level test is 12 passes out of 13 tests.

4.2.System and subsystem reliability assessment using singlelevel priors and data only

Due to the lack of system-level prior information and experimental data for some aerospace systems,system reliability may have to be assessed completely relying on subsystemlevel information.The assessment method based on a system structure with subsystem-level prior and data that has been discussed in Section 3.1 can be employed.Eq.(12)below presents the system reliability and the likelihood function for the given example and testing data in Table 1.

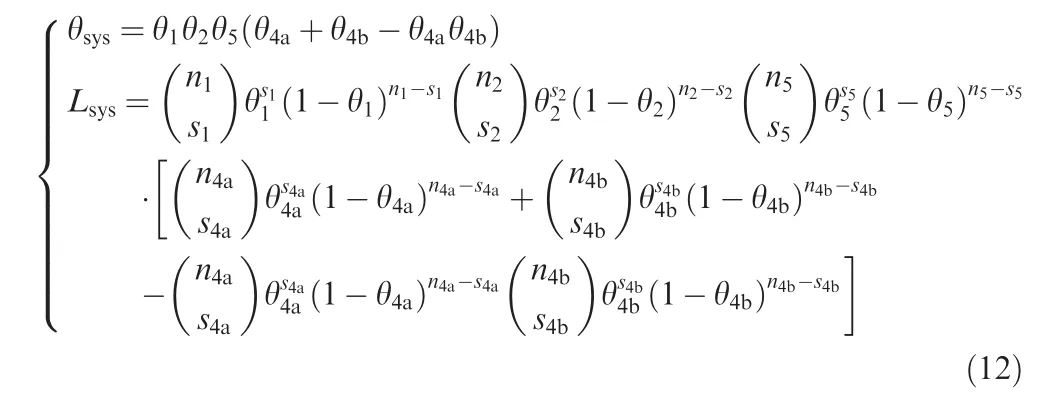
where θi,ni,si,i=1，2，4a，4b,and 5 are the parameters in Bernoulli trials,i.e.,the reliability of each subsystem,the number of total tests,and the number of successes of theith subsystem,respectively.

Prior distributions of subsystems can be obtained through the prior elicitation method discussed in Section 2.1.In this research,one expert was interviewed to provide prior information about the reliabilities of subsystems in the form of mode estimation and confidence levels(Table 2).

When conjugated priors are used,the posterior distribution can be obtained analytically.Fig.5 illustrates the subsystem prior and posterior reliability distributions simulated through the MC method,and the density is dimensionless.The system prior and posterior reliability,in the sixth panel of Fig.5,is derived from the subsystem priors and posteriors based on the system configuration.The posterior modal reliabilities of subsystems 1,4a,and 4b are less than their prior modal reliabilities due to the observed failures from the subsystem testing data(Table 1).The posterior modal reliabilities of subsystems 2 and 5 are very close to their prior modal reliabilities since there is no failure observed from these two subsystems.

In certain scenarios,system-level prior and data are available,while subsystem-level prior and data are limited,such as the reliability performance of a hydraulic valve of an aerospace system in a harsh vacuum environment.In such cases,system reliability can be simply estimated as a single item.In this example,the system reliability posterior distribution is beta（a+y，b+n-y）with the beta prior beta（a，b）,whereyandnare the number of passes and the total number of trials,respectively.A beta（a，b）is referred as the prior distribution of system reliability,which represents prior information centered around θsys,i.e.,a 50%–50%fail versus pass probability.Using the conjugate beta distribution,the posterior distribution ofθsysfollowsan updated beta distribution,i.e.,p（θsys|Ysys）～ beta（13，4）,whereYsysdenotes the system-level test data.

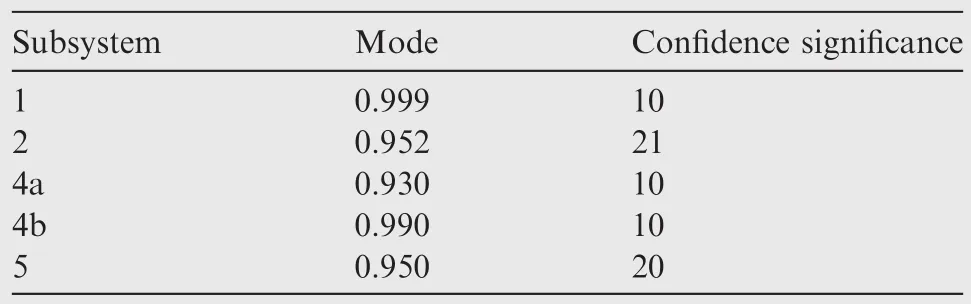
Table 2 Expert estimates on the reliability of each subsystem.

Fig.5 Subsystems and system posterior reliabilities using the subsystem priors and data only.

4.3.System reliability estimation using priors and data from system%and/or subsystems

In this section,the focus is to integrate system-level reliability information with subsystem-level reliability information.In particular,updating the posterior system reliability by pooling the system prior and subsystem priors.The subsystem posterior reliability is also updated by integrating the system-level reliability information through the Bayesian melding method.

4.3.1.System and subsystem reliability estimation usingsubsystem prior and data as well as system prior

In cases of the existence of subsystem prior and test data as well as the system prior reliability,the subsystem posterior distribution can be evaluated based on the updated subsystem prior and the subsystem-level data.Firstly,the updated subsystem prior distribution is evaluated as in Eq.(8).Then,an updated subsystem posterior distribution can be estimated using the updated subsystem prior distribution and the subsystem-level test data.The system posterior distribution can be further derived from the updated subsystem posteriors based on the system structure.Considering the computational advantage of the SIR algorithm over the Metropolis-Hastings method and the separable sampling weights in the posterior inference as in Eq.(10),the adaptive SIR simulation algorithm discussed in Section 3.2.2 is applied to make inference on the subsystem posterior reliability.The number of original sampled importance weights is set to 105,and the number of selected weights and the percentage parameter for determining the threshold weight value are assigned as 1000 and 90%,respectively.The weight splitting process stops when the standard deviation of importance weights is smaller than 100.Fig.6 shows the subsystem posterior from the updated prior and system posterior derived from subsystem posteriors based on the system configuration.For subsystem reliability inference,when system prior information is not incorporated for updating the subsystem prior,the subsystem posterior reliability may be overestimated.Fig.7 shows the updated system prior,the system posterior derived by using the system-level prior information,and the system posterior reliability without using the system-level prior information in Section 4.2.The system posterior modal reliability of 0.521 by integrating the system-level prior with the subsystem prior and data is lower than the system posterior modal reliability of 0.783.This is found using the subsystem prior and data due to the neutral system prior specification of beta（2，2）.

Fig.6 System and subsystem reliability posteriors based on system prior and subsystem prior and data.

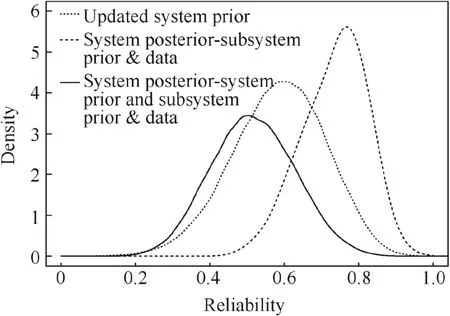
Fig.7 System posteriors reliability using various-level prior and data.

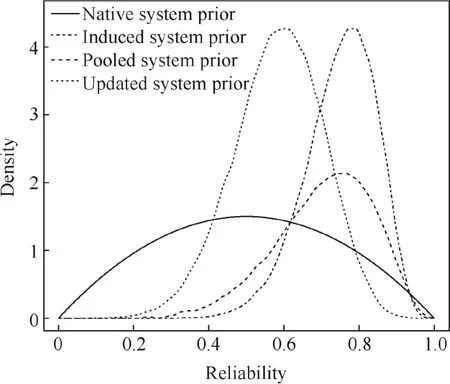
Fig.8 Native,induced,pooled,and updated system prior.

4.3.2.System and subsystem reliability estimation using system prior and data as well as subsystem priors

When the system prior reliability,system-level test data,and the subsystem prior reliability are available,the posterior distribution of system reliability can be evaluated by integrating the pooled system prior reliability with the likelihood function for the system-level data.The pooled system prior distribution is the weighted average of the system native prior and induced system prior reliability as in Eq.(6).Thus,the system posterior reliability based on the pooled system prior integrates the system prior,system data,and subsystem priors.The simulation method for no-closed form system posterior reliability inference uses the MCMC method by introducing proposal distributions.Since it is difficult to obtain full conditionals using Eq.(12),the MH algorithm is suggested with the pooled system prior reliability as the proposal distribution.Fig.8 compares the system native prior distribution,the induced system prior distribution,and the pooled system prior distribution as well as the updated system prior distribution derived from the updated subsystem priors through the system configuration.It is noted that the induced system prior represents the prior information from subsystems only and does not include the native system prior information.The pooled system prior distribution includes both the native and induced system prior information,while the updated system prior integrates the updated subsystem priors through the system structure function.It is observed(Fig.8)that both the pooled and updated system priors balance the native and induced system prior information.Fig.9 compares the system reliability posteriors for the case of using subsystem priors and data only,which uses the pooled and updated system priors with system data.According to the derivation of the pooled and updated system prior distributions(Section 3.2),the lower posterior reliability estimate through the updated system prior compared to that using the pooled system prior indicates that the system prior knowledge has an impact on the subsystem prior update and the system-level posterior reliability inference.

Fig.9 System posterior reliability using subsystem prior and data,and using the pooled and updated system priors and system data.

4.3.3.System and subsystem reliability assessment based on

priors and data from both system and subsystems

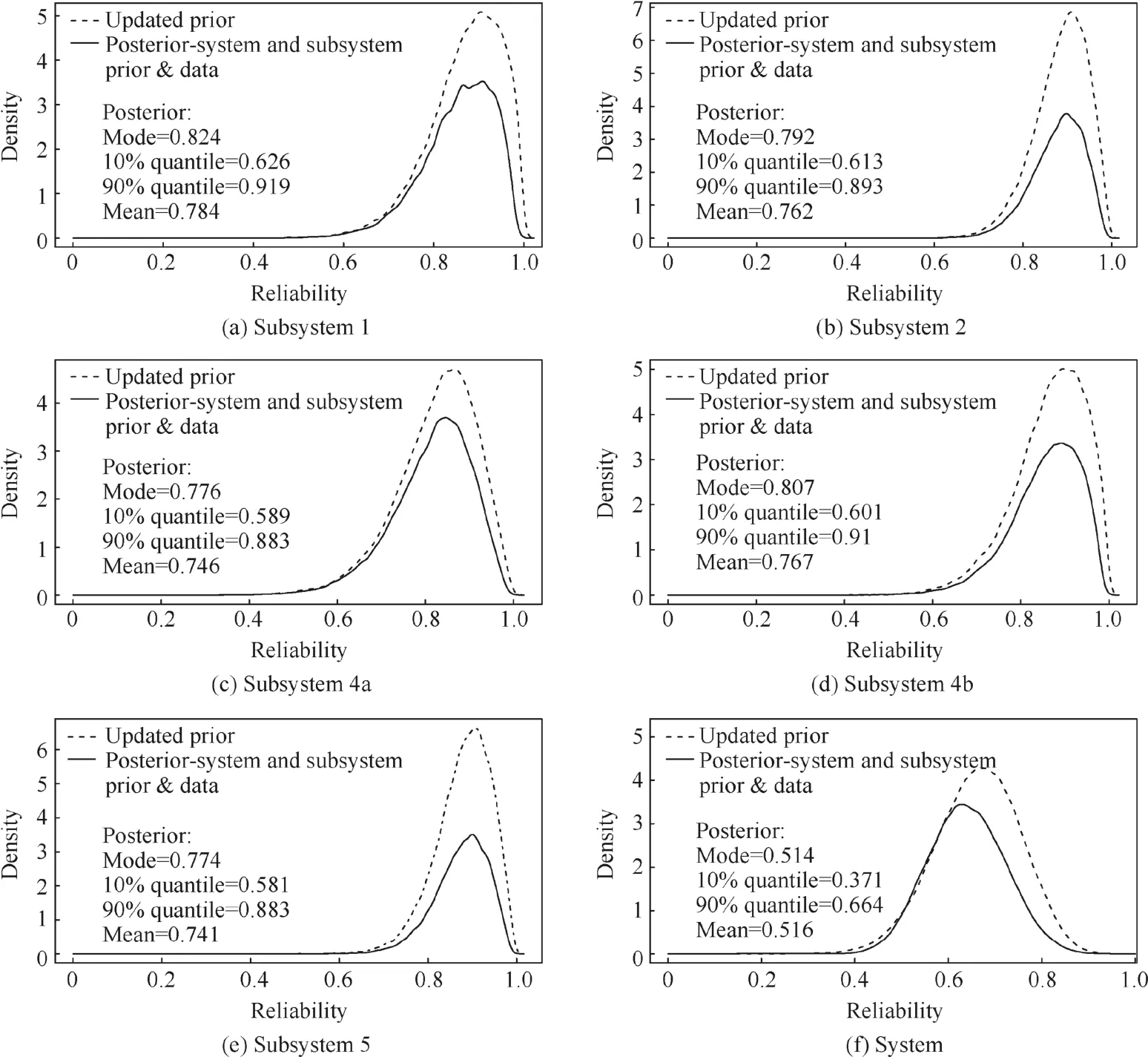
Fig.10 System and subsystem priors and posterior reliabilities using both system-and subsystem-level priors and data.

In cases when priors and test data at both system and subsystem levels are available,the Bayesian melding method discussed in Section 3.2 is an effective way to incorporate multilevel information.Eq.(5)is considered as the deterministic functionM（·）with inputs being the reliabilities of subsystems,θ = ［θ1，θ2，θ4a，θ4b，θ5］T.The pooled prior is obtained in Eq.(6)by assigning a pooling weight α as 0.5.The posterior inference needs to evaluate multiple quantities such as the induced prior,the pooled prior,and the complex likelihood function.In this case,considering the computational efficiency of sampling subsystem priors and evaluating system priors and likelihood functions,the same adaptive SIR algorithm used in Section 4.3.1 is used to make inferences on system and subsystem posterior reliabilities.Fig.10 shows the updated prior and posterior distributions of subsystem and system reliabilities with both system-and subsystem-level test data.Subsystem and system posterior modal reliabilities are less than those using subsystem priors and data as well as the system prior,which can be attributed to the integration of system-level testing data,i.e.,12 successes out of total 13 tests.

For comparison purpose,the posterior system and subsystems reliability distributions evaluated using various available multilevel priors and data are plotted in Fig.11.For the subsystem-level posterior reliability assessment(thefirst 5 panels in Fig.11),the modal reliability with only subsystem prior and data is the highest due to higher subsystem prior specifications.When the system prior information is integrated in addition to the subsystem prior and data,the modal reliability shifts to the left due to a neutral system prior specification.In addition,when system-level data are also available,for subsystems 1,4a,and 4b,due to the observed failed tests,the modal reliability shifts to the furthest left.Since there are no observed failures for subsystems 2 and 5,the modal reliabilities of these two subsystems are very close when using the system prior only in the case of using system prior and data.

At the system level(the 6th panel in Fig.11),only systemlevel data are available.The two system posterior reliability distributions under both pooled and updated system priors are located to the left of the four posterior distributions.This indicates a relative low system success rate,i.e.,12 successes out of a total of 13 tests,can lead to lower posterior system reliability assessment.When only subsystem-level data are available,the posterior system reliability distribution shifts to the right,which can be explained as a higher prior reliability specification at the subsystem level.In summary,the BM method provides a rational mechanism to integrate multiplelevel system and subsystem priors and data for system and subsystem posterior reliability inferences.

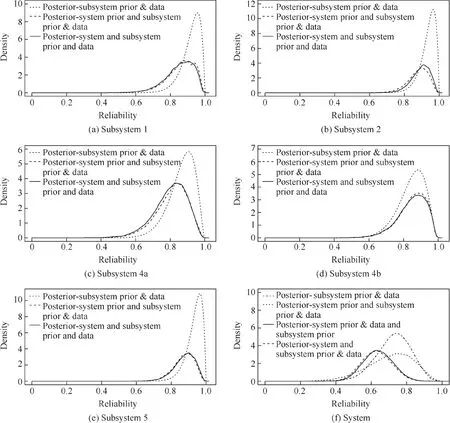
Fig.11 System and subsystem posterior reliability comparison between the four studied scenarios.

5.Conclusions

This paper investigates the applications of various Bayesian methods for system reliability assessment when multilevel reliability information is available.Particularly,four main scenarios in terms of the availability of system and/or subsystem priors and data are discussed.Specific Bayesian inference methods are recommended for updating both system-and subsystem-level posterior reliability distributions.The Baye-sian melding method is proposed to update the subsystem posterior reliability using the proposed SIR simulation algorithm,which has less computational complexity compared to that of the MCMC algorithm when complex priors and likelihood functions are involved.System reliability assessment outcomes are compared using different levels of prior and data information available through the MCMC and adaptive SIR simulation algorithms.Through this study,it is observed that different Bayesian information fusion mechanisms for system-and subsystem-level priors and data can lead to different posterior reliability estimations.When multiple levels of information are integrated through the Bayesian melding method,the reliability inferences are more accurate.However,misspecified information can also overestimate or underestimate reliabilities at both system and subsystem levels.

In the literature,updating subsystem posterior reliability by using system-level prior and data has not been investigated.The studied Bayesian methods using varying multilevel reliability information can be useful for more accurate and efficient system and subsystem reliability evaluation and prediction.The proposed SIR simulation algorithm is applicable for larger-scale system reliability assessment when complex priors and likelihood functions exist.The current work focuses on commonly used binary data,and future work will be extended to multiple types of test data such as lifetime data and degradation data.

1.Sander P,Badoux R.Bayesian methods in reliability.Dordrecht:Springer;1991.

2.Hamada M,Wilson A,Reese CS,Martz H.Bayesian reliability.New York:Springer Science+Business Media;2008.

3.Springer M,Thompson W.Bayesian confidence limits for the product ofNbinomial parameters.Biometrika1966;53(3/4):611–3.

4.Springer M,Thompson W.Bayesian confidence limits for system reliabilityProceedings of the 1969 annual reliability and maintainability symposium.New York:Institute of Electrical and Electronics Engineers;1969.p.515–23.

5.Tang J,Tang K,Moskowitz H.Exact Bayesian estimation of system reliability from component test data.Nal Res Log1997;44(1):127–46.

6.Singh H,Cortellessa V,Cukic B,Gunel E,Bharadwaj V.A Bayesian approach to reliability prediction and assessment of component based systemsProceedings on the 12th international symposiumonsoftwarereliabilityengineering. Piscataway(NJ):IEEE;2001.p.12–21.

7.Mastran D.Incorporating component and system test data into the same assessment:a Bayesian approach.Oper Res1976;34(3):113–20.

8.Mastran D,Singpurwalla N.A Bayesian estimation of reliability of coherent structure.Oper Res1978;26(4):633–72.

9.Martz H,Waller R,Fickas E.Bayesian reliability analysis of series system of binomial subsystem and components.Technometrics1988;30(2):143–54.

10.Martz H,Waller R.Bayesian reliability analysis of complex series/parallel systems of binomial subsystems and components.Technometrics1990;32(4):407–16.

11.Winkler R.The consensus of subjective probability distribution.Manage Sci1968;15(2):B61–75.

12.Hamada M,Martz H,Reese CS,Graves T,Johnson V,Wilson A.A fully Bayesian approach for combining multilevel failure information in fault tree quantification and optimal follow-on resource allocation.Reliab Eng Syst Safe2004;86(3):297–305.

13.Bier V.On the concept of perfect aggregation in Bayesian estimation.Reliab Eng Syst Safe1994;46(3):271–81.

14.Johnson V,Graves T,Hamada M,Reese CS.A Hierarchical model for estimating the reliability of complex systems.Bayes Stat2003;7(2):199–214.

15.Wilson A,Graves T,Hamada M,Reese CS.Advances in data combination,analysis and collection for system reliability assessment.Stat Sci2006;21(4):514–31.

16.Poole D,Raftery A.Inference for deterministic simulation models:the Bayesian melding approach.J Am Stat Assoc2000;95(452):1244–55.

17.Reese CS,Wilson A,Guo J,Hamada M,Johnson V.A Bayesian model for integrating multiple sources of lifetime information in system-reliability assessments.J Qual Techol2011;43(2):127–41.

18.Guo J,Wilson A.Bayesian methods for estimating system reliability using heterogeneous multilevel information.Technometrics2013;54(4):461–72.

19.Rubin D.Bayesianly justifiable and relevant frequency calculations for the applied statistician.Ann Stat1984;12(4):1151–72.

20.Evans M,Swartz T.Methods for approximating integrals in statics with special emphasis on Bayesian integration problems.Stat Sci1995;10(3):254–72.

21.Robert C.Bayesian computational methods.In:Gentle J,Ha¨rdle Y,Mori Y,editors.Handbook of computational statistics(volume I)concepts and fundamentals.Heidelberg:Springer;2004[chapter III.11.11].

22.Geman S,Geman D.Stochastic relaxation,Gibbs distributions and the Bayesian restoration of images.IEEE T Pattern Anal1984;6(6):721–41.

23.Metropolis N,Rosenbluth A,Rosenbluth M,Teller A,Teller E.Equation of state calculations by fast computing machines.J Chem Phys1953;21(6):1087–91.

24.Hastings W.Monte Carlo sampling methods using Markov Chain.Biometrika1970;57(1):97–109.

25.Liang F,Liu C,Carroll R.Advanced Markov Chain Monte Carlo methods.Chichester:John Wiley and Sons;2010.

26.Bedford T,Quigley J,Walls L.Expert elicitation for reliable system design.Stat Sci2006;21(4):428–50.

27.Quigley J,Bedford T,Walls L.Prior distribution elicitation,encyclopedia of statistics in quality and reliability.Hoboken:John Wiley&Sons;2008.

28.Weiler H.The use of incomplete beta functions for prior distribution in binomial sampling.Technometrics1965;7(3):335–47.

29.Meyer M,Booker J.Eliciting and analyzing expert judgment:a practical guide.Philadelphia:ASA-SIAM;2001.

30.Rosenthal J.Optimal proposal distribution and adaptive MCMC.Handbook of Markov Chain Monte Carlo.Boca Raton:Chapman&Hall/CRC;2011[chapter 4].

31.Chib S,Greenberg E.Markov Chain Monte Carlo simulation methods in econometrics.Econ Theor1996;12(3):409–31.

32.Raftery A,Givens G,Zeh J.Inference from a deterministic population dynamics model for bowhead whales.J Am Stat Assoc1995;90(430):402–30.

33.Wolpert R.Comment on ‘‘Inference from a deterministic population dynamics model for bowhead whales”.J Am Stat Assoc1995;90(430):426–7.

34.Genest C,McConway K,Schervish M.Characterization of externally Bayesian pooling operators.AnnStat1986;14(2):487–501.

35.Taddy M,Lee H,Sanso B.Fast inference for statistical inverse problems.Inverse probl2009;25(8):085001.

36.Rubin D.Using SIR algorithm to simulate posterior distributions,Bayesian statistics.Oxford:Clarendon Press;1988.

37.Frigessi A,Martinelli F.Computational complexity of Markov Chain Monte Carlo methods for finite Markov random fields.Biometrika1997;84(1):1–18.

38.Raftery A,Bao L.Estimating and projecting trends in HIV/AIDS generalized epidemics using incremental mixture importance sampling.Biometrics2009;66(4):1162–73.

39.Liang F.Dynamically weighted importance sampling in Monte Carlo computation.J Am Stat Assoc2002;97(459):807–21.

40.Yuan C,Druzdzel M.Improving importance sampling by adaptive split-rejection control in Bayesian network,advances in artificial intelligence.20th conference of the Canadian society for computational studies of intelligence,Canadian AI 2007;2007 May 28–30,Montreal,Canada;2007.p.332–43.

41.Li Z,Mense A.Bayesian reliability modeling for pass/fail systems with sparse data.The 61st annual reliability&maintainability symposium.Palm Harbor:IEEE Press;2015.p.1–7.