Satellite lithium-ion battery remaining useful life estimation with an iterative updated RVM fused with the KF algorithm

Yuchen SONG,Datong LIU,Yandong HOU,Jinxiang YU,Yu PENG

Department of Automatic Test and Control,School of Electrical Engineering and Automation,Harbin Institute of Technology,Harbin 150080,China

1.Introduction

Since a lithium-ion battery wasfirstly used in a United Kingdom satellite called STRV-1d,it has been widely used in many spacecraft including satellites and deep-space detectors.A significant improvement on satellites’total weight reduction is achieved with the huge advantages of gravimetric energy density and volumetric energy density.Lithium-ion batteries have become the third generation of aerospace application power storage batteries.1

As one of the most critical components,a lithium-ion battery is an inevitable sub-system of a spacecraft.2The battery energy storage not only is the solitary power source while a spacecraft operating in a shadow phase,but also provides extra peak power while some high-power payloads working or changing the running orbit.Accurate Remaining Useful Life(RUL)estimation can help realizing the condition-based maintenance schedule and optimizing the task schedule.This is also essential for future autonomous maintenance and autonomous health management.In addition,with the high requirement of the spacecraft long lifetime,i.e.,8–10 years for low-earth orbit satellites,battery RUL estimation can provide more decision-making information for a ground reliability assessment.In particular,for those low-cost and long-lifetime space applications or urgent launching missions,a sufficient on-ground degradation or lifetime test is not permitted.

Besides aerospace applications,lithium-ion batteries have become a crucial part for almost all industrial systems.Performance degradation identification,capacity fade modeling,and RUL estimation have drawn much attention in reliability engineering.Especially,lithium-ion battery RUL estimation has become a research hotspot in thefield of Prognostics and Health Management(PHM).

The approaches for lithium-ion battery RUL estimation can mainly be classified into two categories:model-based and data-driven methods.Model-based methods are generally achieved by building physical degradation models describing lithium-ion battery inner electrochemical reactions.Although complex models can always reveal how irreversible processes impact the performance degradation,model-based methods always involve too many parameters to represent complicated failure mechanisms properly.Furthermore,since a lithium-ion battery is a kind of dynamic nonlinear system,parameters are not consistent under different operating conditions and working loads,which makes it more difficult to identify the parameters.On the other hand,some electrochemical features,i.e.,Solid Electrolyte Interphase(SEI),3Electrochemical Impedance Spectrum(EIS),4etc.,can only be measured under strict conditionsand by high-costinstruments.Thesetesting approaches cannot satisfy the real applications.Thus,for RUL estimation approaches used on spacecraft,it is difficult tofind proper dynamic parameters to match the special inorbit operating conditions for model-based methods.

Data-driven methods estimate the RUL based on historical data and monitoring data.Many data-driven methods have already been applied in battery RUL estimation.Liu et al.5optimized an AutoRegressive(AR)model by combining a nonlinear degradation function to estimate the battery RUL.Liu et al.6utilized Artificial Neural Networks(ANNs)whose network weights are adaptively optimized using the Recursive Levenberg–Marquardt(RLM)method to predict RUL.Lu et al.7proposed a geometrical approach to model the li-ion battery capacity,and four geometrical features were utilized to present the slight changes in the performance degradation.Xing et al.8fused an empirical exponential and a polynomial regression model to predict the remaining useful performance of lithium-ion batteries.Yan et al.9introduced an LS-FDP framework for prognosis,and Lebesgue Sampling(LS)was applied for ‘‘execution only when necessary”.Some other data-driven methods,such as the Naı¨ve Bayes(NB)model,10the Markov Chain Mote Carlo approach,11the Support Vector Machine(SVM),12,13the Particle Filter(PF),14–17Gaussian Process Regression(GPR)18,etc.,are all widely used in battery RUL estimation.The Relevance Vector Machine(RVM)algorithm is also adopted in battery RUL prediction with high learning capability and easy training process.19The RVM represents a generalized linear model under the Bayesian framework,20so it can provide uncertainty management ability which is valuable for lithium-ion battery health management.21

Saha et al.22firstly attempted to use the RVM in battery prognostics,in which the RVM-PF approach provided the uncertainty presentation with a probability density function.Wang et al.23applied the RVM to acquire relevance vectors to indicate the battery capacity fading and cycle life.A three-parameter conditional capacity degradation model was established at the same time.Widodo et al.24proposed a battery health assessment framework based on a sample entropy of the discharge voltage.The RVM algorithm was used to predict the RUL and provide the uncertainty presentation.Li et al.25developed a multistep-ahead prediction model based on the mean entropy and the RVM was applied for the State of Health(SoH)and RUL prediction.Liu et al.15optimized the RVM with an incremental learning strategy to satisfy the requirements of dynamic training and on-line learning capabilities.Zhang et al.26weakened the noise during a battery test by using wavelet and estimated the RUL with the RVM optimized by differential evolution.Hu et al.27used the RVM to learn the relationship between the capacity and its chargerelated features.An RVM regression model trained offline was used to infer the unknown capacity from a set of charge-related characteristics.

As mentioned above,the RVM has been widely used in lithium-ion battery RUL estimation.However,its poor performance of long-term prediction is the challenging issue that has limited its applications.28The statisticalfiltering algorithm is also applied to estimate battery RUL,but in real applications,the measurement equation is hard to determine owing to the dynamic feature of a lithium-ion battery.A fusion framework is proposed in this paper to solve the above two bottlenecks.Single-step prediction is conducted once the RVM model be trained.The predicted estimator is considered as the measurement value in the Kalman Filter(KF).The estimator is optimized and the uncertainty involved isfiltered by a statespace equation.The training data set is extended with this optimized observer,and the model is retrained with this updated training data set.The main contribution in this paper can be summarized as follows:(A)to improve the poor performance of long-term prediction,we propose an iterative updated method for the RVM.The training data set is updated when the prediction value is optimized by the KF.Then the model is re-trained to obtain new relevance vectors and coefficient matrix.The capacity for next cycle is predicted after the update;(B)a data-driven method is applied as the measurement equation applied in the statisticalfiltering method.With this fusion framework,a state-space model can be established.Then,the KF can fuse the prediction value with the physical degradation model to get an optimized capacity prediction.

The rest of this paper is organized as follows.Section 2 introduces the principle of the RVM algorithm and the KF algorithm briefly.In Section 3,the proposed hybrid strategy for battery RUL prediction is described in detail.Experimental results are shown in Section 4 based on a commercial battery data set.Finally,conclusions and future work are discussed in Section 5.

2.Methodology

2.1.Relevance vector machine

Battery RUL prediction is a kind of long-term regression prediction problem.In other words,it’s a kind of relevance vector regression essentially.

The RVM was proposed by Bishop and Tipping29based on the support vector machine.Bayesian inference is applied on the kernel method in the RVM.The output of the RVM model can be expressed as

According to Bayesian inference principles,p（ti|x）is defined as the normal distribution oftiwith a mean ofy（x）and a variance of σ2,andp（ti|x）can be presented asp（ti|x）～N（y（x），σ2）.Considering thattiare independent of each other,the likelihood of the complete data set is

As ω is defined as the weight vector of the output of the RVM model,the maximum likelihood estimates of ω and σ2from Eq.(3)will lead to severe over-fitting.To avoid the problem of over-fitting,a prior Gaussian distribution with zero-mean is applied to add a constraint on ω.This prior distribution is defined as

where α = ［α0，α1，...，αN］ isa vectorofN+1 hyperparameters.Each hyper-parameter is independently associated with a weight,which controls the strength of the prior over its associated weight,and this is the main method to get a sparse model determinately.

The Gamma distributions of α and the noise variance σ2can be presented as

where Gamma（αi|a，b）= Γ（α）-1baαa-1e-bα.

2.2.Hyper-parameter optimization

Once there is a vector of new measurement values,the prediction under a sparse Bayesian learning framework can be described as

wheretN+1is the target value of the new inputxN+1.However,this equation is not analytically soluble.The Monte Carlo sample algorithm can be used to make approximate calculation,but the process of the method is too complicated as well as the huge amount of calculation,so we usually solve the equation with iterative approximation.

Eq.(5)can be factorized as follows:

The posterior of the parameters can be calculated based on the Bayesian inference framework,and the posterior distribution also has a form of Gaussian distribution as

The posterior covariance and mean of weight can be presented as

where A=diag（α0，α1，···，αN）.

As for real applications,lots of hyper-parameters are close to 0,as well as the posterior distributions of many weights approach to 0.In the relevance vector regression model,the data samples whose weights are unequal to 0 are called Relevance Vectors(RVs).These RVs show the core features of the whole data set.

Thus,the sparse Bayesian learning method is changed tofind themostsuitable posteriordistribution ofhyperparameters using a reasonable optimization method.

In Eq.(3),the likelihood distribution of the output is calculated by the marginal integration of parameters as

Then,the likelihood of hyper-parameters can be described as

In Eq.(11),the maximum analytic solutions of α and σ2are unable to obtain.An iterative estimation method is applied in computing.αniewand （σ2）neware the presentations of α and σ2during the iteration process,which can be expressed as

where γi=1- αiΣii,μiis mean of theith posterior weight,and Σiiis the diagonal element of the posterior variance matrix Σ.The calculation is conducted iteratively until the results are convergent.

For the newly updated samplex*,estimations are made for the corresponding target t*.Thusp（t*|t）～N（μTΦ（x*），σ2*）follows a normal distribution,in which

2.3.Learning algorithm for the RVM

A training method is the essential part of implementing the achieved RVM with a likelihood function and prior knowledge.The likelihood function describes the potential characteristicsoftraining samples.Priorknowledgeshowsthe complexity of the model,which enhances the generalization capability of the test samples.The main training algorithms can be classified into the MacKay iterative learning algorithm(basic learning algorithm),30the sequential sparse Bayesian learning algorithm,31and the EM iterative learning algorithm.32

In this work,the MacKay iterative learning algorithm is used for RVM training.The steps for training sparse Bayesian learning with the MacKay algorithm are as follows.

Step 1.Initialization:｛αi｝ and σ2.

Step 2.Calculation:the posterior means and posterior variance based on Eqs.(9)and(10).

Step 3.Update:｛αi｝ and σ2using Eqs.(13)and(14).

Step 4.Conduct Steps 2 and 3 iteratively till the loops reach the maximum number or the gradient of the output meets the convergence requirement.

Step 5.Screen:the weight ωicorresponding to αiin which αi＞ αmaxas well as those column vectors with an index of i in the kernel matrix Φ.αmaxis considered to be infinite,but in real applications,we set αmaxwith a huge value such as αmax=1.0 × 105.

Step 6.Prediction:apply the convergence parameter in the prediction if there is a new data sample to obtain the prediction result with a probability formula.

The value of αmaxshould be taken into consider to improve the prediction performance.Too many or too few relevance vectors both decrease the estimation accuracy.

3.Iterative updated RVM for lithium-ion battery RUL estimation

In this paper,our purpose is fusing the RVM model and the KF algorithm together to get more accurate degradation prediction and estimate the RUL.

Due to the sparsity of the RVM algorithm and long-term prediction challenging in RUL estimation,it’s difficult to get accurate prediction results.The iteration framework of the RVM can achievebatterycapacityprediction with an improved long-term prediction performance.This promotion is meaningful for capacity degradation modeling.

On the other hand,since the measurement noise and other uncertainties,the KF is applied to reduce the uncertainty and obtain more accurate results.The outputs of the RVM model are applied as the measurement equation in the state-space model,which can overcome the difficulties of building a complex state equation.This fusion makes the approach more suitable for dynamic applications.

3.1.Iterative updating and prediction strategy

Although the RVM can get sparse relevance to describe the feature of data,the long-term prediction performance is not satisfactory.Fig.1 shows the long-term prediction curve when the RVM model is trained by the early-stage data.The curve converges so fast that the result will lose the accuracy after a few cycles.

The relevance vectors and coefficients matrix are not updated in a typical RVM algorithm.This leads to an unacceptable accuracy in prediction results.The early-stage data can’t present the whole degradation trend,while the relevance vectors and coefficients matrix can’t present the later stage at the same time.Hence,we use an idea of divide-and-conquer to solve the problem in this paper.Long-term prediction can be divided into some short-term predictions.From the partially enlarged detail in Fig.1,we can see that the degradation curve prediction is precious.Therefore,in our proposed framework,the prediction values of nextncycles are regarded as the real degradation values which are applied to re-train the RVM model.With the single-step predictionfinished,results can be applied to update the training data set,and subsequent short-term estimation can be conducted.Theflowchart of this iterative updating and prediction strategy is shown in Fig.2.

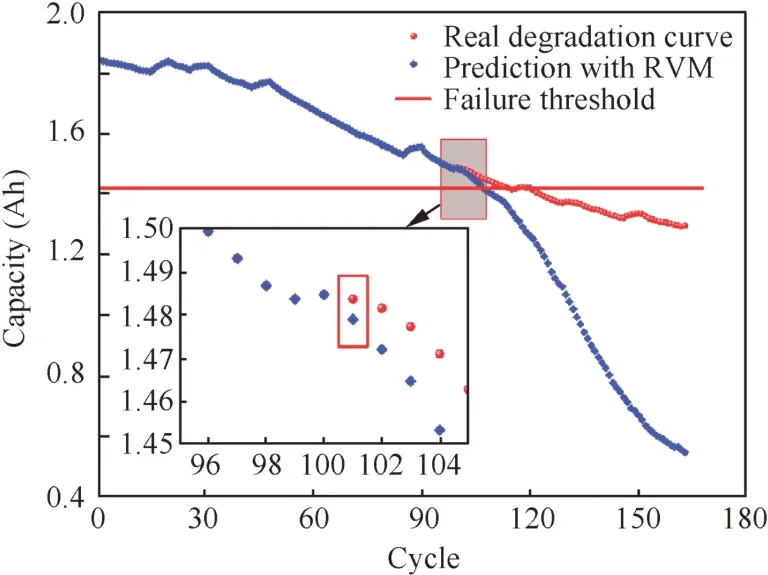
Fig.1 RVM long-term prediction curve.

Fig.2 RVM predictionflowchart.

The iterative updating method is described as follows.

Step 1.Initialize the training data set equation reference｛（x1，y1），（x2，y2），...，（xn，yn）｝ and RVM model parameters.

Step 2.Train the model and obtain the relevance vectors and coefficient matrix.

Step 3.Predict the next cycle’s output yn+1based on the input xn+1and the relevance vectors and coefficient matrix obtained in Step 2.

Step 4.Update the training data set with （xn+1，yn+1）,and the format of the updated training data set is｛（x1，y1），（x2，y2），...，（xn，yn），（xn+1，yn+1）｝.

Iterate Steps 2 to 3 until the prediction value reaches the failure threshold.

3.2.Dynamic state system model establishment

Data-driven methods ignore the real physical principles during model training and estimating.Model-based prognostics methods will take those physical reactions into account.Thus we use the statisticalfilter method(KF)to fuse the data-driven method and physically-based approach.The critical part of this kind of method is establishing a Dynamic State System(DSS)model.

The DDS model can describe many dynamic processes in statistics,signal processing,and many other domains.The DSS model is made up by an unmeasurable time-varying state sequence xkand a group of observation sequence yk.

The DSS model can be described as

wherek=1，2，...，xkand ykare two discrete time sequences.xk∈ ℜLxrepresents the system state atk.f（xk-1，wk）is a state transition equation,which may not be linear.wk∈ℜLwis the noise vector of the system atk.yk∈ℜLyis the observation vector of timek,which depends on the system’s state vector.The observation equationh:ℜLx×ℜLx→Iy⊆ℜLxdescribes the relationship between the observation vectors and future states.vk∈ℜLvis the noise vector at thekmoment which is independent of wk.Eq.(17)is the state transition equation that describes the dynamic process of the system state vector.Eq.(18)is always named as observation equation.

The battery degradation is a kind of Markov process;in other words,with the timekdynamically changed,the state vector xkpresents the feature of the system indirectly.However,the observation vector is collected at eachk.The battery degradation is a kind offirst-order Markov process,the state vector xkand the measurement ykare independent of each other.Suppose that the prior probability density of state xkis initialized as p（x0）.The statistical description of the DSS model is as follows:

(1)Corresponding to the state transition equation,the state transition probability density can be defined as p（xk|xk-1）.

(2)Corresponding to the observation equation,the system state observation likelihood probability density is presented as p（yk|xk）.

Fig.3 shows the state transition probability density and likelihood probability of observation in the DSS model.

In our framework,the state transition equation for a lithium-ion battery can be described as the following equation:

whereCkstands the capacity in thekth cycle,Δtkis the rest time interval between thekth cycle and the(k+1)th cycle,and β1and β2are the parameters to be identified,ηcis defined as the columbic efficiency.

A lithium-ion battery has different characteristics in different working conditions,which brings huge difficulty to determinetheobservation equation.Thesameobservation equation model may not be suitable for different conditions.As mentioned above,data-driven methods have great advantages in model establishment and parameters determination.Thus as for our framework,we fuse the data-driven method with the model-based method by the KF.We set Eq.(17)as the state transition function in the DSS model.At the same time,the output from the RVM is set as the measurement value of the DSS model.With this dynamic state system model,the data-driven method and the battery capacity degradation model can be fused to obtain an optimized estimation of battery remaining useful life.

3.3.RVM-KF algorithm for lithium-ion battery remaining useful life prediction

The framework of the iterative updating RVM-KF algorithm is illustrated in Fig.4.Define that the initial training data set is TD,the new prediction input isxn+1,the new prediction output from the RVM isy′n+1,the optimized prediction value from the KF isyn+1,the newly updated training data is TDN,the relevance vector set isRVs,and the coefficient matrix isFi.

The iterative updating method is described as follows:

Step 1.Initialize the training data set ｛（x1，y1），（x2，y2），...，（xn，yn）｝,RVM model parameters,and Kalman filter parameters.

Step 2.Train the RVM model with the MacKay algorithm and obtain the model withRVsandFi.

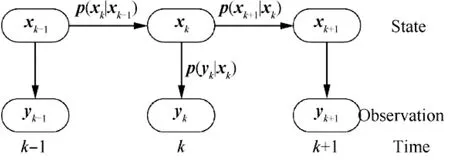
Fig.3 Dynamic state system model.

Fig.4 Dataflowchart of the proposed framework.

Step 3.Conduct a one-step prediction with the input xn+1,RVs,andFi.The predicted result is y′n+1.

Step 4.Optimize the RVM prediction output yn+1by the Kalman Filter.The optimized predicted value is presented as yn+1.

Step 5.Update the training data set with the input xn+1and the output yn+1.

Step 6.Determine whether the output yn+1is less than the failure threshold.If yn+1reaches the failure threshold,then stop iterative and convert yn+1into cycle life time.If not,iterate from Step 2 to Step 5 until yn+1is less than the failure threshold.

The detailed iterative RVM-KF algorithmflow is presented in Fig.5.

4.Experimental results and discussion

To evaluate the proposed battery RUL prediction algorithm,we adopt a battery data set from NASA Prognostics Center of Excellence(PCoE)33,34to implement a series of experiments.

Fig.5 Detailed iterative RVM-KF algorithmflow.

4.1.Data sets and evaluation criteria

4.1.1.NASA PCoE battery data set

The data set was sampled from a battery prognostic testbed at NASA comprising commercially available lithium-ion 18650 rechargeable batteries.The lithium-ion batteries were run through 3 different operational profiles(charge,discharge,and impedance)at room temperature.Charging was carried out in a constant current mode at 1.5 A until the battery voltage reached 4.2 V,and then continued in a Constant Voltage(CV)mode until the charge current dropped to 20 mA.Discharge was carried out at a Constant Current(CC)level of 2 A until the battery voltage fell to 2.7 V,2.5 V,and 2.2 V for batteries#05,#06,and#07,respectively.Impedance measurement was operated through an EIS frequency sweep from 0.1 Hz to 5 kHz.The experiments were stopped when the batteries reached the End-of-Life(EoL)criterion,which was a 30%fading in rated capacity.Here,the experiment has been stopped when the capacity of the lithium-ion battery life threshold is set to 1.38 Ah.The capacity degradation curves of the three batteries are shown in Fig.6.

4.1.2.Satellite battery data set

The test is conducted on a real lithium-ion battery applied in a satellite.The lithium-ion battery is run in 2 different working conditions.One is the DDC condition which means that double charge and discharge current is utilized to accelerate the degradation of the battery.In this working situation,the charge current is constant at 17 A.Once the voltage reaches 4.15 V,constant-voltage charging is used instead.The discharge voltage is 20 A.In each test cycle,the charging time is about 27 min while the discharge takes about 18.5 min.The other working condition is named as CDC.This working condition is set to simulate a real task situation on orbit.In this case,the charging current is held at 8.5 A till the voltage attains 4.1 V.The discharge current is 10 A.In each test cycle,the current time is about 54 min while the discharge procession is maintained about 37 min.As the battery is used in the satellite,the capacity of each cycle can’t be measured.Therefore,in this experiment,voltage is used as the parameter to reflect the battery degradation.Fig.7 shows the degradation trends of two tested batteries.

Fig.6 PCoE battery degradation curves.

Fig.7 Satellite battery degradation curves.

Fig.8 RUL prediction for battery#05 at a starting point of 100 cycles.

Table 1 Parameters in the capacity fade model.

Fig.9 RUL prediction comparison between RVM and iterative RVM-KF.

4.1.3.Evaluation criteria

Four evaluation criteria are used to measure and demonstrate the accuracy of the proposed method.

error:absolute error of RUL prediction

RUL_err:relative error of RUL prediction

MAE:mean absolute error of capacity

RMAE:root mean absolute error

4.2.Experimental results

4.2.1.PCoE battery data experiments

We conduct experiments based on PCoE battery data sets in which RUL estimations are conducted with different stages of lifetime.

The parameters in the capacity degradation model is shown in Table 1.As for the parameterCkin Eq.(19),it is determinedby the RVM output of cyclek(here,cyclekmeans thefirst cycle after the prediction start point).

Table 2 Prediction results with different starting points of different data sets.

We implement the RUL estimation with the PCoE battery data set,in which different starting points are selected.Fig.8 indicates the predicted curve with the starting point at 80 of battery#05 and Table 2 shows the predicted results.In Table 2,we can see that all of the predicted RUL errors are less than 10 cycles at different starting points.In addition,the MAE and RMSE are less than 0.01 which indicates high estimation precision in the whole prediction process.With the initialized training data length getting longer,the prediction result becomes more accurate.

Then,we compare our proposed framework with the basic RVM algorithm.The battery#05 data set with a starting point at 80 cycles is used.Fig.9 shows the estimation curve with different starting points of different batteries and Table 3 presents the prediction results.

From Table 3 and Fig.9,we canfind that the iterative RVM-KF method improves the prediction accuracy about 100%compared to the basic RVM algorithm.The MAE and RMSE also decrease with the iterative updating in the proposed framework.

The AR model is known as an efficient data model to achieve long-term regression prediction,so in this paper,we further compare our framework with the AR model to evaluate the performance.Table 4 shows the prediction error in those two different approaches.The battery#05 data set is used in this experiment.

From Table 4,our proposed method shows a higher prediction accuracy than that of the autoregressive model.In summary,our proposed iterative approach has a great RUL prediction performance,and could be used in real applications to evaluate the reliability of aerospace lithium-ion batteries.

Table 3 Comparison between RVM algorithm and iterative RVM-KF algorithm.

Table 4 Parameters in capacity fade model.

Fig.10 Prediction curves of different working conditions and different starting points.

4.2.2.Satellite battery data experiments

We conduct experiments utilizing real satellite battery data sets.The RUL is estimated from different stages of lifetime.Both of the two different data sets from different working conditions are applied in these experiments to analyze the adaptability of our framework in aerospace applications.

Table 5 presents the quantitative results and Fig.10 hows the predicted degradation curves with different starting points in different working conditions.

Table 5 Prediction results with different starting points of different data sets.

From Table 5 and Fig.10,we can see that our proposed method can predict the degradation trend in high accuracy.Moreover,with the training data sets becoming longer,betterfitting results can we obtain.This means that our method can satisfy the requirements of long-life-time satellite lithium-ion battery RUL prediction.However,with the test conduction continuing,more accurate prognostic results can be expected.

5.Conclusions and future work

This paper explores an iterative RVM-KF algorithm for lithium-ion battery RUL estimation.The main contributions of this work can be concluded as:(A)aiming at the poor performance in long-term prediction of the RVM algorithm,an iterative updating framework is proposed for battery RUL prediction.Considering the noise and measurement uncertainties,the KF is utilized to optimize andfilter the RVM output.Each cycle’s predictor is applied to update the training data set and retrain the model for iterative prediction;(B)to establish an observation equation for the dynamic characteristics of lithium-ion batteries,the data-driven RVM predictor is regarded as the observer instead of the traditional equation format in a dynamic state system model,and the output of the data-driven method can be fused and optimized with the model-based method at the same time.This iterative updating RVM-KF approach shows a great potential in lithium-ion battery applications and can be extended to some other related areas.

In the future,we will optimize the retraining process of the RVM algorithm in each iterative prediction to decrease the computing complexity.Thus,this optimized strategy can guarantee the on-line performance of the proposed framework for real-time applications.Moreover,the robustness and stability also need to be further verified.Additional evaluations need to be conducted on other lithium-ion batteries under more complicated operating conditions or charging/discharging profiles.

Acknowledgements

This work was co-supported in part by the National Natural Science Foundation of China(Nos.61301205 and 61571160),and the Natural Scientific Research Innovation Foundation at Harbin Institute of Technology(No.HIT.NSRIF.2014017).

1.Zhang J,Lee J.A review on prognostics and health monitoring of Li-ion battery.J Power Sources2011;196(15):6007–14.

2.Rufus F,Lee S,Thakker A.Health monitoring algorithms for space application batteries.In:Proceedings of prognostics and health management;2008 Oct 6–9;Denver,CO,USA;2008.

3.Eddahech A,Briat O,Bertrand N,Dele´tage JY,Vinassa JM.Behavior and state-of-health monitoring of Li-ion batteries using impedance spectroscopy and recurrent neural networks.Int J Elec Power2012;42(1):487–94.

4.Verma P,Maire P,Nova´k P.A review of the features and analyses of the solid electrolyte interphase in Li-ion batteries.Electrochimica Acta2010;55(22):6332–41.

5.Liu DT,Luo Y,Liu J,Peng Y,Guo L,Pecht M.Lithium-ion battery remaining useful life estimation based on fusion nonlinear degradation AR model and RPF algorithm.Neural Comput Appl2014;25(3–4):557–72.

6.Liu J,Saxena A,Goebel K,Saha B,Wang W.An adaptive recurrent neural network for remaining useful life prediction of lithium-ion batteries.In:Proceeding of annual conference of the Prognostics and Health Management Society;2010.

7.Lu C,Tao L,Fan H.Li-ion battery capacity estimation:a geometrical approach.J Power Sources2014;261:141–7.

8.Xing Y,Ma EW,Tsui KL,Pecht M.An ensemble model for predicting the remaining useful performance of lithium-ion batteries.Microelectron Reliab2013;53(6):811–20.

9.Yan W,Zhang B,Wang X,Dou W,Wang J.Lebesgue-samplingbased diagnosis and prognosis for lithium-ion batteries.IEEE T Ind Electron2016;63(3):1804–12.

10.Ng SS,Xing Y,Tsui KL.A naive Bayes model for robust remaining useful life prediction of lithium-ion battery.Appl Energ2014;118(4):114–23.

11.Liao H,Tian Z.A framework for predicting the remaining useful life of a single unit under time-varying operating conditions.IIE Trans2013;45(9):964–80.

12.Pattipati B,Pattipati K,Christopherson JP,Namburu SM,Prokhorov DV,Qiao L.Automotive battery management systemsProceedings of 2008 IEEE autotestcon.Piscataway:IEEE Press;2008.p.581–6.

13.Nuhic A,Terzimehic T,Soczka-Guth T,Buchholz M,Dietmayer K.Health diagnosis and remaining useful life prognostics of lithium-ion batteries using data-driven methods.J Power Sources2013;239:680–8.

14.Miao Q,Xie L,Cui H,Liang W,Pecht M.Remaining useful life prediction of lithium-ion battery with unscented particlefilter technique.Microelectron Reliab2013;53(6):805–10.

15.Saha B,Goebel K.Modeling Li-ion battery capacity depletion in a particlefiltering framework.In:Proceedings of the annual conference of the prognostics and health management society;2009.p.2909–24.

16.Edwards D,Orchard ME,Tang L,Goebel K,Vachtsevanos G.Impact of input uncertainty on failure prognostic algorithms:extending the remaining useful life of nonlinear systems.In:Proceeding of annual conference of the Prognostics and Health Management Society;2010.

17.Acun˜a DE,Orchard ME.Particle-filtering-based failure prognosis via sigma-points:application to Lithium-Ion battery State-of-Charge monitoring.Mech Syst Signal Pr2017;85:827–48.

18.Liu D,Pang J,Zhou J,Peng Y,Pecht M.Prognostics for state of health estimation of lithium-ion batteries based on combination Gaussian process functional regression.Microelectron Reliab2013;53(6):832–9.

19.Liu D,Zhou J,Pan D,Peng Y,Peng X.Lithium-ion battery remaining useful life estimation with an optimized relevance vector machinealgorithm with incrementallearning.Measurement2015;63:143–51.

20.Tipping ME.TherelevancevectormachineProceedingsof advances in neural information processing systems.Cambridge(MA):MIT Press;2000.p.652–8.

21.Saha B,Goebel K.Uncertainty management for diagnostics and prognostics of batteries using Bayesian techniques2008 IEEE aerospace conference.Piscataway:IEEE Press;2008.p.1–8.

22.Saha B,Poll S,Goebel K,Christophersen J.An integrated approach to battery health monitoring using bayesian regression and state estimation.In:Proceedings of 2007 IEEE Autotestcon;2007.p.646–53.

23.Wang D,Miao Q,Pecht M.Prognostics of lithium-ion batteries based on relevance vectors and a conditional three-parameter capacity degradation model.JPowerSources2013;239(10):253–64.

24.Widodo A,Shim MC,Caesarendra W,Yang BS.Intelligent prognostics for battery health monitoring based on sample entropy.Expert Syst Appl2011;38(9):11763–9.

25.Li H,Pan D,Chen CP.Intelligent prognostics for battery health monitoring using the mean entropy and relevance vector machine.IEEE Trans Cybern2014;44(7):851–62.

26.Zhang C,He Y,Yuan L,Xiang S,Wang J.Prognostics of lithiumion batteries based on wavelet denoising and DE-RVM.Comput Intel Neurosc2015(1);14.

27.Hu C,Jain G,Schmidt C,Strief C,Sullivan M.Online estimation of lithium-ion battery capacity using sparse Bayesian learning.J Power Sources2015;289:105–13.

28.Zhou J,Liu D,Peng Y,Peng X.Combined sparse Bayesian learning strategy for remaining useful life forecasting of lithiumion battery.In:2012 second international conference on instrumentation,measurement,computer,communicationandcontrol(IMCCC);2012.p.457–61.

29.Bishop CM,Tipping ME.Variational relevance vector machines.In:Proceedings of the Sixteenth conference on Uncertainty in artificial intelligence;2000.p.46–53.

30.Tipping ME.Sparse Bayesian learning and the relevance vector machine.J Mach Learn Res2001;1(3):211–44.

31.Tipping ME,Faul AC.Fast marginal likelihood maximisation for sparse Bayesian models.In:Proceedings of the ninth international workshop on artificial intelligence&statistics;2003.p.3–6.

32.Dempster AP,Laird NM,Rubin DB.Maximum likelihood from incomplete data via the em algorithm.J R Stat Soc B1977;39(1):1–38.

33.Saha B,Goebel K,Poll S,Christophersen J.Prognostics methods for battery health monitoring using a Bayesian framework.IEEE T Instrum Meas2009;58(2):291–6.

34.Saha B,Goebel K,Christophersen J.Comparison of prognostic algorithms for estimating remaining useful life of batteries.T I Meas Control2009;31(3–4):293–308.