超临界二氧化碳部分冷却布雷顿循环参数优化

方立军， 杨 雪， 孙立超， 任忠强

(华北电力大学 能源动力与机械工程学院， 河北保定 071003)

从2002年第四代核能论坛提出第四代核能系统使用超临界流体以来，世界各国学者都在致力寻求效率高、投资少、应用稳定的布雷顿循环技术[1]，其中具有代表性的有：(1)美国麻省理工学院研究的再压缩布雷顿循环[2]；(2)日本东京工业大学在再压缩布雷顿循环的基础上，增加中间压缩和中间冷却过程的部分冷却循环[3]。

相比于再压缩循环，部分冷却循环具有效率高、吸热端差大、与显热太阳能电站相结合的优点[4-5]。超临界二氧化碳(S-CO2)动力循环首先由苏尔寿公司1948年作为一个专利项目提出[6]；Mahmood、Turchi等[7-8]通过EES(Engineering Equation Solver)对结合太阳能电站的不

同布雷顿循环进行分析，发现部分冷却布雷顿循环在透平入口温度高于600 ℃时效率最高；Harvego等[9]发现具有再热的布雷顿循环比无再热的布雷顿循环效率高1%～3%。

2012年，中国科学院发明“一种基于超临界二氧化碳的发电系统”专利，将我国对S-CO2布雷顿循环的研究提上议程[10]；随后各大高校也开展对其研究[11-13]。目前的研究主要集中在对使用于核能的中低温再压缩循环。

笔者以结合太阳能电站为例，通过EES对使用于中高温的部分冷却布雷顿循环进行分析，为以后中高温火电、太阳能电站获得高效率、低成本的动力循环提供参考。

1 循环简介

图1为S-CO2部分冷却布雷顿循环简单示意图，图2为相应的T-S图。

1→2—工质在高压透平膨胀(T1)做功；2→3—工质在再热器中定压吸热；3→4—工质在低压透平中膨胀做功(T2)；4→5—工质在高温回热器冷却过程；5→6—工质在低温回热器冷却过程；6→7—工质在预冷器中冷却过程；7→8—工质在预压压缩机(C1)压缩过程；8→12—分流后部分工质在再压压缩机(C3)压缩过程；8→9—部分工质在中间冷却器冷却过程；9→10—部分工质在主压缩机(C2)中压缩过程；10→11—部分工质在低温回热器吸热过程；13→14—汇合后工质在高温回热器吸热过程；14→1—工质在吸热器吸热过程。

图1 具有一级再热的S-CO2部分冷却循环示意图

图2 具有一级再热的S-CO2部分冷却循环T-S图

2 循环建模和分析

2.1 热力学模型

笔者对一级再热S-CO2部分冷却布雷顿循环进行热力学建模。压缩机等熵效率为ηc，透平等熵效率为ηt，循环压比比为rpr。

(1)

式中：phigh为循环最高压力；pin为预压缩机入口压力；plow为循环最低压力。

为防止回热器出现“夹点”问题而导致传热恶化，设高、低温回热器最小温差为ΔT，则T5=T13+ΔT，T6=T10+ΔT。

模型假设：(1)循环所有过程都已经处于稳定状态；(2)忽略换热器及管道压降；(3)循环各设备绝热。系统模型是借助EES根据热力学第一定律建立，具体可见表1(rsr为通过再压缩机的分流比；h为比焓；下标表示工况点)。

表1 具有一级再热的S-CO2部分冷却布雷顿循环数学模型

2.2 主要参数确定

笔者选用主压缩机入口为初始点，以工质流量为单位质量为例，其相关参数见表2[14-16]。

表2 主要参数

3 计算结果及分析

3.1 再热压力对循环热效率的影响

图3是当压缩机入口温度为32 ℃、入口压力为7.7 MPa、透平入口温度为650 ℃、透平入口压力为20 MPa时，再热压力对循环热效率的影响。

图3 再热压力对循环热效率的影响

从图3可以看出：当再热压力与第一透平压力的比值为0.5左右时，循环热效率最高，约为0.457。在实际循环中，最佳再热压力还与管道压降、回热器压降等因素有关，实际最佳再热压力比最优再热压力值略高。对于传统的蒸汽朗肯循环再热机组，其最佳再热蒸汽压力为主蒸汽压力的25%～30%。

3.2 循环压比比对循环热效率的影响

图4为循环压比比对循环热效率的影响。

图4 循环压比比rpr对循环热效率的影响

对rpr从0.2到0.7进行分析，从图4可以看出：在相同的透平入口温度和压力下，循环热效率随着rpr的增大先增大再减少，即存在一个最佳值rpr=0.4。当rpr较大时，即循环压比较小，此时透平做功增长率高于压气机功耗增长率。当rpr较小时，即循环压比较大，透平做功增长率低于压缩机耗功增长率。因此当rpr增大时，循环热效率有先增大后减少的趋势。

3.3 主压缩机入口温度对循环热效率的影响

图5为主压缩机入口温度对循环热效率的影响。

图5 主压缩机入口温度Tc1,in对循环热效率的影响

从图5可以看出：随着压缩机入口温度的增加，循环热效率减少，并且当压缩机入口温度越偏离临界温度，增加入口温度时循环热效率减少的幅度降低。主要是因为CO2在临界附近时密度较高，偏离临界点时密度降低，压缩机耗功增加，循环热效率降低；另外，为了防止压缩机内流体发生相变，进气温度不得低于CO2临界温度，因此选择压缩机入口温度为32 ℃，此时循环效率最高。

同时从图5还可以看出：随着透平入口温度的增加，循环效率增大；但透平入口温度的增加也需考虑材料强度、设备高温腐蚀、结晶及设备的造价等因素。因此，需要综合考虑透平入口温度。

3.4 回热器夹点温差对循环热效率的影响

图6为回热器夹点温差对循环效率的影响。

图6 回热器夹点温差ΔT对循环热效率的影响

从图6可以看出：随着回热器夹点温差的增大，循环热效率降低。主要是因为夹点温差增大，回热器效率降低，循环热效率降低。

3.5 压缩机等熵效率对循环热效率的影响

图7为透平入口温度为650 ℃、透平入口压力为20 MPa、压缩机入口温度为32 ℃时，压缩机等熵效率对循环热效率的影响。

图7 ηc对循环热效率的影响

由图7可以看出：循环热效率随着压缩机效率的升高而增大。压缩机效率的提高使得压缩机功耗减少，从而导致热效率增大。

3.6 透平等熵效率对循环热效率的影响

图8为压缩机入口温度为32 ℃、入口压力为7.7 MPa、透平入口温度为650 ℃、透平入口压力为20 MPa时，透平等熵效率对循环热效率的影响。

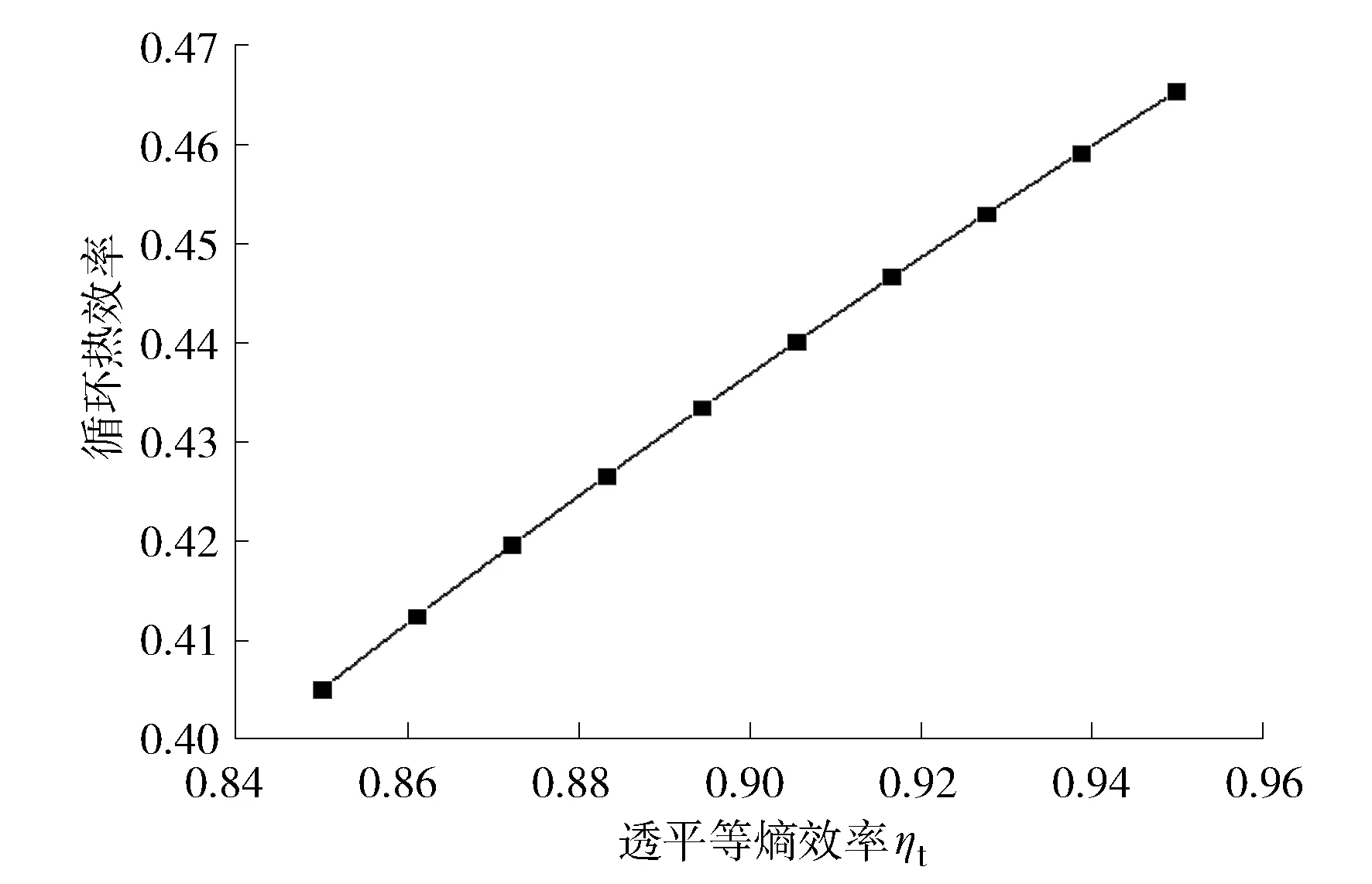
图8 ηt对循环热效率的影响

从图8可以看出：循环热效率随着透平等熵效率的增大为增大。在一定条件下，透平等熵效率的增加使得透平做功能力增强，循环热效率增大。

比较图7和图8可以看出：透平效率对循环热效率的影响大于压缩机效率对循环热效率的影响。当透平效率增加1%时，循环热效率增加0.8%，而压缩机效率增加1%时，循环热效率增加0.5%。这主要是因为透平对进出口温度的变化更为敏感。另外，对于采用透平膨胀机的系统而言，为提高透平等熵效率可以采取以下措施：(1)优化结构设计，减少导热损失；(2)优化基本参数；(3)获得较高转速，保持转子系统稳定运行。

4 结语

笔者分析了影响S-CO2部分冷却布雷顿循环各影响参数对循环热效率的影响，得到如下结论：

(1) 压缩机入口温度、压力接近CO2临界点时，压缩机耗工最少，循环热效率最高。

(2) 对于具有再热的S-CO2部分冷却布雷顿循环来说，其再热压力存在一个最佳值，约为第一透平压力的0.5倍。

(3) 透平入口温度增加，循环热效率增大。

(4) 随着回热器夹点温差的增大，循环热效率降低。

(5) 相比于压缩机等熵效率对循环热效率的影响，透平效率对循环热效率的影响更显著。

[1] 李照煦, 卫广刚. 展望第四代核能系统之一: 超临界水冷堆——专访彭士禄院士[J]. 中国核电, 2009, 2(4): 290-291.

[2] 高峰, 孙嵘, 刘水根, 等. 二氧化碳发电前沿技术发展简述[J]. 海军工程大学学报(综合版), 2015, 12(4): 92-96.

[3] Verson B D, Conboy T M, Pasch J J, et al. Supercritical CO2, Brayton cycles for solar-thermal energy[J]. Applied Energy, 2013, 111(4):957-970.

[4] HO C K, CARLSON M, GARG P, et al. Cost and performance tradeoffs of alternative solar-driven S-CO2Brayton cycle configurations[C]//ASME 2015, International Conference on Energy Sustainability Collocated with the ASME 2015 Power Conference, the ASME 2015 13th International Conference on Fuel Cell Science, Engineering and Technology, and the ASME 2015 Nuclear Forum. San Diego, CA: ASME, 2015.

[5] PADILLA R V, TOO Y C S, BENITO R, et al. Exergetic analysis of supercritical CO2Brayton cycles integrated with solar central receivers[J]. Applied Energy, 2015, 148: 348-365.

[6] Wright S A, Pickard P S, Fuller R, et al. Supercritical CO2Brayton cycle power generation development program and initial test results[C]//ASME 2009 Power Conference.Brussels,Belgium:ASME,2009.

[7] MOHAGHEGHI M, KAPAT J. Thermodynamic optimization of recuperated S-CO2Brayton cycles for solar tower applications[C]//ASME Turbo Expo 2013: Turbine Technical Conference and Exposition. San Antonio, Texas, USA: ASME, 2013.

[8] NEISES T, TURCHI C. A comparison of supercritical carbon dioxide power cycle configurations with an emphasis on CSP applications[J]. Energy Procedia, 2013, 49: 1187-1196.

[9] HARVEGO E A, MCKELLAR M G. Optimization and comparison of direct and indirect supercritical carbon dioxide power plant cycles for nuclear applications[C]//ASME 2011 International Mechanical Engineering Congress and Exposition. Denver, Colorado, USA: American Society of Mechanical Engineers, 2011: 75-81.

[10] 王磊, 景玉鹏. 一种基于超临界二氧化碳的发电系统: 102606241A[P]. 2012-07-25.

[11] 段承杰, 杨小勇,王捷. 超临界二氧化碳布雷顿循环的参数优化[J]. 原子能科学技术, 2011, 45(12): 1489-1494.

[12] 黄雯婷,赵航,邓清华, 等. 超临界CO2部分预冷循环特性分析及优化研究[J]. 工程热物理学报, 2016, 37(2): 235-239.

[13] 梁墩煌, 张尧立, 郭奇勋, 等. 核反应堆系统中以超临界二氧化碳为工质的热力循环过程的建模与分析[J]. 厦门大学学报(自然版), 2015, 54(5): 608-613.

[14] TURCHI C S, MA Z W, NEISES T, et al. Thermodynamic

study of advanced supercritical carbon dioxide power cycles for high performance concentrating solar power systems[C]//ASME 2012 6th International Conference on Energy Sustainability Collocated with the ASME 2012 10th International Conference on Fuel Cell Science, Engineering and Technology. San Diego, California, USA: ASME, 2012: 1928-1936.

[15] AHN Y, LEE J, KIM S G, et al. Design consideration of supercritical CO2power cycle integral experiment loop[J]. Energy, 2015, 86: 115-127.

[16] WRIGHT S A, RADEL R F, VERNON M E, et al. Operation and analysis of a supercritical CO2Brayton cycle[R]. Albuquerque, NM: Sandia National Laboratories, 2010.