基于非差模型的GPS卫星实时钟差估计精度分析

，，，

(长安大学 地质工程与测绘学院，西安 710054)

0 引言

实时精密单点定位技术(Real Time Precise Point Positioning，RT-PPP)已成为当前全球卫星导航系统(Global Navigation Satellite System，GNSS)领域的研究热点，也将是目前乃至未来实时高精度动态定位的主要技术手段之一。其中，实时精密卫星轨道和实时精密卫星钟差是实现RT-PPP应用的两大关键技术[1-3]。目前，国际GNSS服务组织(International GNSS Service，IGS)提供的全球定位系统(Global Positioning System，GPS)超快速预报轨道产品精度为5cm，最终轨道产品精度为2.5cm，两者精度量级相当。然而，GPS超快速预报钟差产品精度仅为3ns，等效距离误差为0.9m，远低于标称精度为75ps的最终钟差产品[4]。虽然GPS超快速预报轨道产品能够满足时间和精度要求，但是GPS实时卫星钟差的精度和稳定性限制了RT-PPP的精度，直接制约了其在大气研究、时间传递、低轨卫星精密定轨等方面的精密应用。另一方面，钟差的内插或者外推精度远远不如轨道的外推精度，在较短的时间内，外推或内插的结果误差就可达到数米，这一点对实时精密单点定位也非常不利。

针对这种情况，国内不少机构和组织也在开展实时GPS精密轨道和钟差的相关研究，如武汉大学、同济大学、长安大学等[5-7]。实时钟差估计多采用历元间差分方法，以提高处理效率，保证钟差产品的实时性。通过在历元间求差，能够消除大量的模糊度参数，只保留数量相对较少的卫星钟差、接收机钟差和对流层参数，因此处理效率较高[8-9]。近年来有学者研究了基于非差观测量的实时钟差估计以及非差和双差混合差分的钟差估计方法[10-12]。利用非差观测量进行实时钟差估计能够保留模糊度参数，为后续双差模糊度固定和卫星硬件延迟估计提供可能。鉴于此，本文采用非差观测模型对卫星钟差进行实时解算，通过算例分析得出，采用最终轨道估计的实时钟差精度在0.2ns左右，采用实时轨道估计的实时钟差精度在0.25ns左右。

1 非差卫星钟差估计模型

对于非差卫星钟差模型，一般采用消电离层组合观测值。单个测站单颗卫星的观测值，非差载波相位和伪距观测值误差方程如下：

利用由上述公式建立的误差方程，未知参数包括接收机钟差、卫星钟差、对流层延迟和模糊度，参数求解方法可采用序贯最小二乘。针对模糊度参数和对流层湿延迟参数，在分段时间内对流层湿延迟参数是不变的，在没有发生周跳时卫星模糊度参数也是不变的，因此将其作为分段非时变参数。

2 实时钟差估计算法流程

非差模型的实时钟差估计是利用实时数据预处理后的伪距、载波观测值，轨道及其他辅助文件，采用非差模型实时解算卫星钟差。其算法流程主要包括卫星天线相位中心改正、潮汐改正、地球自转改正等各项误差改正，非差观测模型组建，卫星钟差实时解算，坏测站剔除和解算精度评估，对流层和模糊度参数约束，钟差参考基准选择几个方面。非差模型的实时钟差估计算法流程如图1所示。

图1 非差模型的实时钟差估计算法流程Fig.1 Real-time clock estimation algorithmfor un-differenced model

在钟差估计过程中，首先读取所有测站的观测数据并确定解算基准测站钟，读取轨道数据、地球自转参数、天线相位中心和硬件延迟偏差等数据，然后进行潮汐误差、相对论误差和天线相位缠绕等误差的改正，确定对流层干延迟和湿延迟投影系数，最后建立非差估计方程，采用序贯最小二乘进行参数估计。

因为GPS量测值是站星之间的相对时间延迟，这意味着不能同时确定所有的卫星和接收机钟差，必须先固定一个基准钟，再求匹配该基准钟的相对钟差。已有专家证明只要保证基准钟的钟差精度都优于10-16s，相对钟差的系统性偏差完全可以被接收机钟差吸收，不影响定位结果[13]，因此本文引入某个外接高精度原子钟的测站接收机钟作为基准钟。另外，为了得到更可靠的钟差结果，在第一次解算结束后，根据钟差估计结果得出各测站每颗卫星的残差值，根据其值进行后验控制，剔除各测站残差较大的卫星。

为了全面地分析基于非差模型的GPS卫星实时钟差估计精度，本文利用区域和全球测站分别解算实时钟差，两者在解算时采用的策略一致，但是考虑到区域测站所形成的卫星观测弧段不完整，区域钟差与全球钟差的精度评估方法会有所区别。

3 算例分析

3.1 钟差精度评估方法

在钟差精度评估时，首先选择一个参考卫星，将实时解算的钟差与最终钟差产品分别与各自的参考卫星钟差作差，消除基准不同对钟差结果的影响，而后再在各自消除基准钟影响的计算结果之间作差，所得的二次差能够较好地反应钟差参数的估计效果[14]。因此，本文采用二次差的标准差(Standard Deviation，STD)作为实时钟差估计精度，具体公式为

当采用区域数据实时解算卫星钟差时，可观测到的卫星弧度是不连续的，每1h所有测站能观测到的卫星都在变化，所以本文每小时选择一次参考卫星(原则：观测时长最长的卫星作为参考卫星)，每小时统计一次STD，然后对一天的STD取平均作为当天的钟差精度。当进行全球实时钟差解算时，可观测到的卫星弧度是连续的，所以一天内选择同一颗卫星作为参考卫星，每天统计一次STD作为当天的钟差精度。

3.2 区域实时钟差估计精度分析

为了分析区域实时钟差估计的精度，本文选择欧洲区20个能够提供高频观测数据的监测站作为实验站点进行试验验证，测站展图如图2所示。

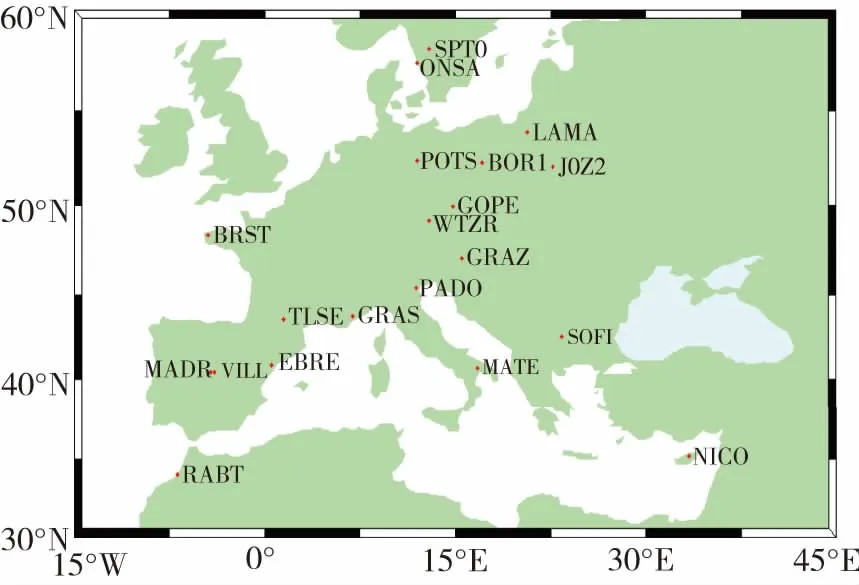
图2 欧洲区域实时钟差解算的测站分布Fig.2 Distribution of station used for real-time clockestimation in European region

采用IGS的最终轨道产品，以及欧洲区域20个测站2015年1月1日—2015年3月31日1s高频观测数据实时解算GPS卫星钟差，将获取的钟差结果与IGS最终精密钟差(30s)进行二次差比较，统计其平均STD值。结果如图3所示。

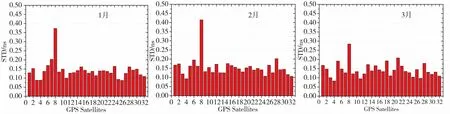
图3 欧洲区钟差平均估计精度Fig.3 Average accuracy of clock estimation in European region

从图3可以看出 ，采用IGS最终轨道实时解算GPS区域卫星钟差，估计精度基本处于0.15ns，其中G08卫星的实时钟差精度较差，是因为此段时间内G08卫星的观测数据较少。统计钟差精度的平均值、最差值和最优值，结果如表1所示。

表1 欧洲区钟差平均估计精度

从表1可以看出，采用IGS最终轨道产品，以及欧洲区域20个测站2015年1月1日—3月31日1s高频观测数据实时解算卫星钟差，1月份的平均估计精度为0.141ns，2月份的平均估计精度为0.155ns，3月份的估计精度为0.143ns，连续90天平均估计精度为0.145ns。除了G08号卫星外，钟差精度总体较为平稳。

3.3 全球区域实时钟差估计精度分析

为了分析全球实时钟差估计的精度，本文选择全球范围内80个能够提供高频观测数据的监测站作为实验站点进行试验验证，测站展图如图4所示。

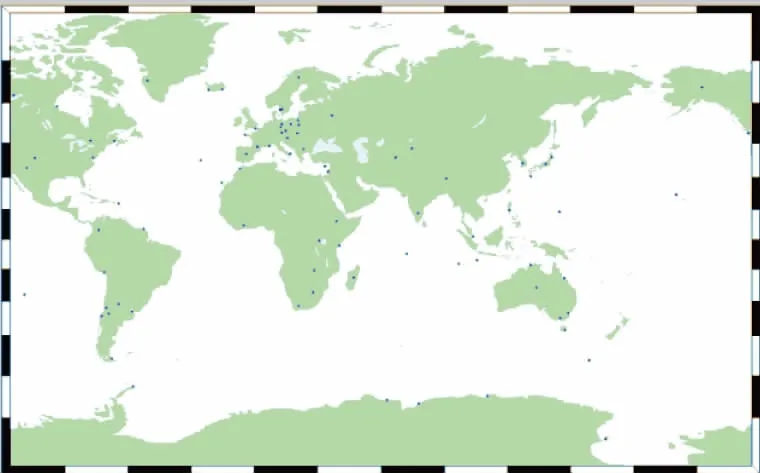
图4 全球区域实时钟差解算的测站分布Fig.4 Distribution of station used for real-time clockestimation in Global region

采用IGS的最终轨道产品，以及全球80个测站2016年1月1日—3日1s高频观测数据实时解算GPS卫星钟差，将获取的钟差结果与IGS最终精密钟差(30s)进行二次差比较，统计其STD值。结果如图5所示(G01为参考钟)。

图5 全球区钟差平均估计精度Fig.5 Average accuracy of clock estimation in Global region

从图5可以看出，采用IGS最终轨道实时解算GPS全球卫星钟差，估计精度基本处于0.2ns。统计钟差精度的平均值、最差值和最优值，结果如表2所示。

表2 全球区钟差平均估计精度

从表2可以看出，采用IGS最终轨道产品，以及全球80个测站2016年1月1日—3日1s高频观测数据实时解算GPS卫星钟差，001天的估计精度为0.221ns，002天的估计精度为0.192ns，003天的估计精度为0.198ns，连续3天平均估计精度为0.204ns。钟差精度总体较为平稳，偶尔会出现比较大的现象。

3.4 IGS实时钟差产品精度评估及对比

为了分析实时估计的卫星钟差与IGS实时钟差产品的差异，采用IGS实时轨道产品，以及3.3节算例中全球80个测站2016年1月1日—3日1s高频观测数据实时解算GPS卫星钟差，将获取的钟差结果与IGS最终精密钟差(30s)进行二次差比较，统计其STD值；同时将IGS的实时钟差产品与IGS最终精密钟差(30s)进行二次差比较，统计其STD值。将两种产品获得的STD值进行对比，结果如图6所示(G01为参考钟)。

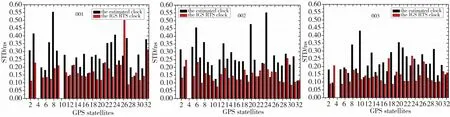
图6 实时估计钟差和IGS实时钟差产品精度对比Fig.6 Accuracy comparison of real-time estimation of clock and IGS real-time clock product

从图6可以看出，采用IGS实时轨道实时解算卫星钟差，钟差精度基本在0.3ns以下，IGS实时钟差产品的精度基本在0.2ns以下。实时估计的卫星钟差相比IGS实时钟差产品较差，这是由于IGS实时轨道和钟差产品的解算方案、解算软件以及所采用的数据均一致，而本文实时估计的钟差在很多方面与其不同，如误差改正模型、数据质量控制方法、观测模型、残差控制策略、测站数目及分布、基准钟和约束条件等，解算得到的结果符合性和相容性都会有差异，且两种实时钟差产品在精度评定时选择IGS最终钟差产品为参考，这对IGS实时钟差产品的评估也会有利。统计两种产品钟差精度的平均值、最差值和最优值，结果如表3所示。

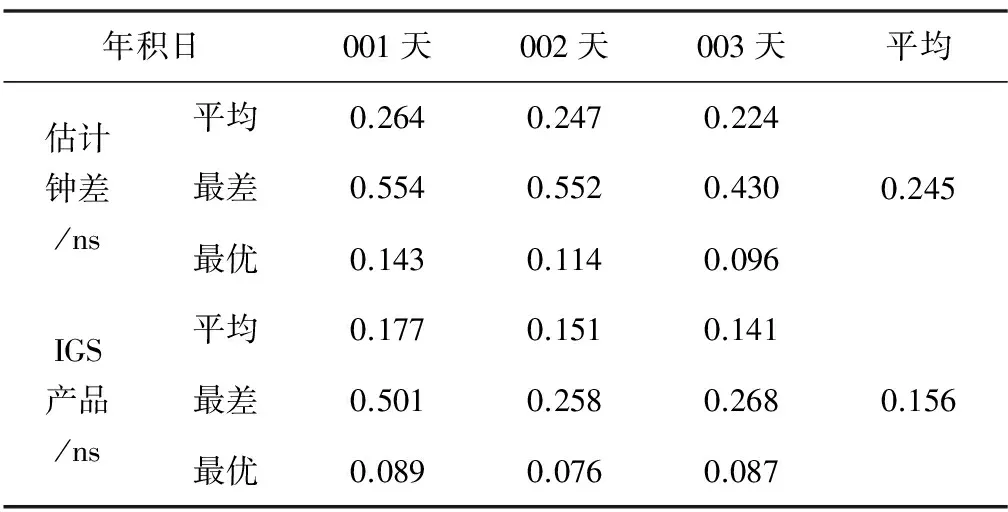
表3 实时估计钟差和IGS实时钟差产品精度对比

从表3可以看出，采用IGS实时轨道产品，以及全球80个测站2016年1月1日—3日1s高频观测数据实时解算卫星钟差，001天的估计精度为0.264ns，002天的估计精度为0.247ns，003天的估计精度为0.224ns，连续三天平均估计精度为0.245ns；IGS实时钟差产品001天的估计精度为0.177ns，002天的估计精度为0.151ns，003天的估计精度为0.141ns，连续三天平均精度为0.156ns。从结果可以看出，目前GPS实时钟差精度能达到0.2ns以内。

4 结论

本文通过分析实时卫星钟差估计的解算过程，实现了基于非差模型的GPS卫星实时钟差估计，利用区域和全球数据、最终和实时轨道分别求解实时钟差，并将其与IGS实时钟差产品进行对比，分析了GPS实时钟差产品的精度，得出以下结论：采用IGS最终轨道产品实时解算卫星钟差，区域平均钟差估计精度为0.145ns，全球平均钟差估计精度为0.204ns；采用IGS实时轨道产品实时解算卫星钟差，平均钟差估计精度为0.245ns；IGS实时钟差产品平均精度为0.2ns以内。实时估计的钟差和IGS实时钟差产品精度差异有很大一部分是由于双方采用的钟差解算策略不同造成，IGS实时钟差产品和IGS实时轨道产品是同一软件求解得到，符合性更好，且两种实时钟差产品在精度评定时选择IGS最终钟差产品为参考，这对IGS实时钟差产品的评估也会有利。

本文只分析了GPS卫星的实时钟差精度，北斗卫星导航系统目前正在启动全球化布设，下一步将对北斗卫星的实时钟差精度进行分析。

[1] 施闯，楼益栋，宋伟伟，等． 广域实时精密定位原型系统及初步结果[J]． 武汉大学学报(信息科学版)，2009，34(11)：1271-1274．

[2] 宋伟伟． 导航卫星实时精密钟差确定及实时精密单点定位理论方法研究[D]． 武汉：武汉大学，2011．

[3] 易重海． 实时精密单点定位理论与应用研究[D]．长沙：中南大学，2011．

[4] http://igsws.unavco.org/components/prods.html.

[5] 蔡华，赵齐乐，楼益栋． 精密卫星钟差确定系统的实现与精度分析[J]． 武汉大学学报(信息科学版)，2009，34(11)：1293-1296．

[6] 李浩军，王解先，王虎，等． 基于GNSS网络的卫星精密钟差估计及结果分析[J]. 武汉大学学报(信息科学版)，2010，35(8)：1001-1003．

[7] Fu W, Zhang Q, Huang G, et al. Performance analysis of real-time BDS clock estimation with different orbit accuracy[C]//China Satellite Navigation Conference (CSNC). Changsha, 2016：99-106.

[8] 李黎，匡翠林，朱建军，等． 基于IGU预报轨道实时估计精密卫星钟差[J]． 大地测量与地球动力学，2011，31(2)：111-116．

[9] 楼益栋，施闯，周小青，等． GPS精密卫星钟差估计与分析[J]． 武汉大学学报(信息科学版)，2009，34(1)：88-91．

[10] 李星星，徐运，王磊． 非差导航卫星实时/事后精密钟差估计[J]．武汉大学学报(信息科学版)，2010，35(6)：661-664．

[11] 赵齐乐，戴志强，王广兴，等．利用非差观测量估计北斗卫星实时精密钟差[J]． 武汉大学学报(信息科学版)，2016，41(5)：686-691．

[12] 何明宪，李星星，李盼，等． 基于非差与历元差分两种观测模型估计精密卫星钟差的方法比较[J]. 大地测量与地球动力学，2011，31(1)：95-99．

[13] 叶世榕． 非差相位精密单点定位理论与实现[D]． 武汉：武汉大学，2002．

[14] 刘伟平，郝金明，于合理，等． 利用非差观测量确定导航卫星精密轨道与钟差的方法研究[J]． 大地测量与地球动力学，2014，34(1)：169-172．