基于星敏感器的卫星姿态估计方法研究

，，

(1.火箭军指挥学院， 武汉 430012；2.空军驻湖南地区军事代表室，长沙 410100；3.空军驻河南地区军事代表室，郑州 450006)

0 引言

现代小卫星技术已有20余年的发展历史,经过不断的研究试验,在技术上得到了全面迅速的提高。小卫星有质量小、体积小、成本低、研制周期短、功能密度大及发射灵活等特点,在通信、对地观测、行星探测、科学技术验证等多个领域得到了广泛应用。限于质量与功耗的约束常采用无陀螺定姿方案,利用卫星姿态动力学方程结合星敏感器的测量信息实现姿态确定,常用算法是将姿态动力学方程中的干扰力矩项增广为状态变量增广卡尔曼滤波器[1]。干扰力矩是随卫星轨道运行作周期性变化的量,在使用过程中发现,在干扰力矩变化较快的时间段,姿态估计准确度较低,而在干扰力矩变化较为平缓的时间段,姿态估计结果良好。为克服干扰力矩变化给姿态估计结果精度带来的影响,本文从增广卡尔曼滤波的基本原理出发,详细分析了干扰力矩变化影响姿态估计精度的原因[2],并从不同侧面提出了两种不同的改进算法:1)增广自适应卡尔曼滤波器(Adaptive Augmented Extended Kalman Filter, AAEKF)算法,依据前一时间段的干扰力矩估计结果,估算干扰力矩的变化率,依据估计出的变化率自适应调整系统的伪随机噪声,使滤波器能更好地跟踪上干扰力矩的变化,同时姿态估计精度也得到提高。2)增广强跟踪卡尔曼滤波器(Augmented Strong Tracking Extended Kalman Filter, ASTEKF)算法,将干扰力矩视为模型中的参数,干扰力矩变化过快导致算法无法准确辨识干扰力矩大小,致使动力学模型中干扰力矩参数失配,姿态估计精度降低,将强跟踪的思想引入到增广卡尔曼滤波器中,可以有效地降低因为模型参数失配对姿态估计精度的影响。文中通过仿真试验的方式,对三种动力学姿态估计器的性能作了详细的分析,验证了改进后的动力学姿态估计器提高姿态估计精度的能力。

1 无陀螺卫星姿态确定系统描述

1.1 姿态确定系统的状态方程

无陀螺卫星姿态确定系统由于没有陀螺仪提供角速率信息,必须在运动学方程的基础上引入姿态动力学方程作为对角速率信息的补充。因此姿态确定系统的状态方程包含有运动学方程和动力学方程,具体形式如下所示[1，3]。

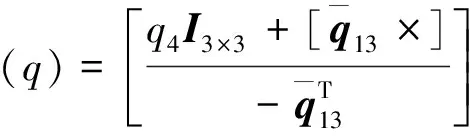
Tc是动量轮以外的控制力矩,Td是干扰力矩,h是动量轮产生的动量矩,J是卫星的惯量矩阵。

1.2 姿态确定系统的观测方程

姿态确定系统从星敏感器获得矢量观测信息,至少需要2个不平行的观测矢量才能确定卫星的姿态。假定星敏感器本体系坐标轴方向和卫星本体系坐标轴方向一致,则系统观测方程可以写为

CS=A(q)·CI+υ

其中:

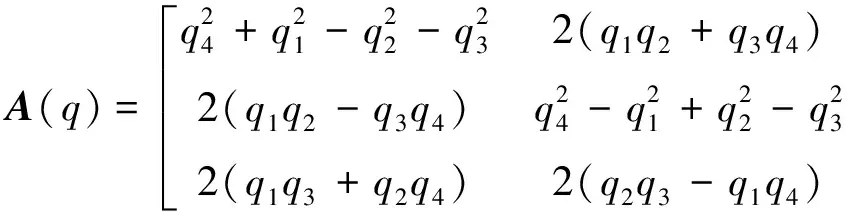
是卫星轨道坐标系到星敏感器本体系转换矩阵的四元数形式,CI是参考矢量在卫星轨道坐标系中的表示,CS是参考矢量在星敏感器本体系中的表示,υ是测量白噪声。

2 动力学姿态估计器的设计

2.1 传统增广卡尔曼滤波

非线性系统的状态方程和测量方程如下所示,状态方程是连续形式的,而测量方程是离散形式[4-5]。

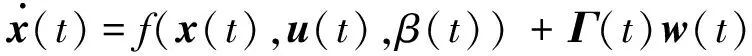
z(tk)=h(x(tk),u(tk),β(tk))+v(tk)

其中,x(t)是状态矢量,z(t)是测量矢量,u(t)是输入矢量,β是系统参数,Γ(t)是系统噪声分布矩阵,w(t)是系统噪声矢量,v(t)是测量噪声矢量。满足如下条件

E[w(t)]=0

E[v(tk)]=0

E[w(t)vT(tk)]=0

E[w(t)wT(τ)]=Q(t)δ(t-τ)

E[v(tk)vT(tj)]=R(tk)δkj

若将非线性系统参数β(t)增广为状态矢量,则增广后的状态矢量为

其中,nβ是随机噪声,定义为增广状态的随机变化率,方差根据实际情况可调,满足

结合上式,系统状态方程可以改写为

对于上面的非线性状态方程,无法直接利用普通的卡尔曼滤波算法,需对非线性模型进行一阶泰勒展开,并将连续状态模型离散化,则卡尔曼滤波器的计算流程如下面各式所示[4-5]。

预测方程:

xa(t0|0)=xa(t0)

式中:

Φa(tk|k-1)=eFa(tk)Δt

校正方程:

K(tk)=Pa(tk|k-1)HT(tk)[H(tk)Pa(tk|k-1)·

HT(tk)+R(tk)]-1

xa(tk|k)=xa(tk|k-1)+K(tk)[z(tk)-

h(xa(tk|k-1),u(tk))]

Pa(tk|k) =[I-K(tk)H(tk)]Pa(tk|k-1)

= [I-K(tk)H(tk)]Pa(tk|k-1)·

[I-K(tk)H(tk)]T+

K(tk)Ra(tk)KT(tk)

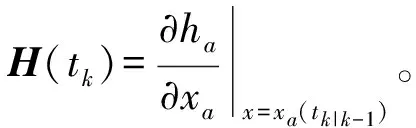
2.2 增广自适应卡尔曼滤波器

依据文献[2,6]中的论述,增广卡尔曼滤波对增广状态的估计原理实际上是极小方差准则下的随机逼近,与增广状态的逼近能力与增广状态随机变化率nβ的方差大小有关。增大随机变化率的方差,可以增强卡尔曼滤波器对时变增广状态的跟踪能力,但是也会增大滤波器的带宽,使滤波结果不够平滑;反之减小随机变化率的方差可以得到较为平滑的结果,但又无法跟踪上增广状态随时间的变化。若能够在滤波过程中依据实时状态对增广状态的随机变化率进行在线调整,即在增广状态变化较慢的时间段采用较小的随机变化率,在增广状态变化较快的时间段采用较大的随机变化率,不仅能够较好地跟踪上增广状态的变化,也能有效控制估计结果的随机噪声。

具体的调整机制是采用增广状态的实时估计结果,近似计算出最近一个时间段内增广状态的变化率,将增广状态的随机变化率方差写成近似估计出的增广状态的变化率的单调递增函数,本文的单调递增函数选取F[x]=xxT,具体形式如下:

Qnβ(tk)=Qnβ(t0)F[εκβ(tk)]

其中，Δt是滤波间隔时间,m是估计增广状态变化率的时间窗内滤波次数,ε是压缩因子。给定Qnβ(t0)值之后可依据滤波结果计算出Qnβ(tk),用Qnβ(tk)代替2.1节中增广卡尔曼滤波算法中的Qnβ进行运算即可。

2.3 增广强跟踪卡尔曼滤波器

当模型参数发生变化时,滤波器过程参数会与模型参数失配,造成滤波器状态估值偏离系统真实状态。反映在输出残差序列上就是残差序列不再相互正交,此时只要在线适当调整增益矩阵,使得输出残差序列仍相互正交,则可强迫滤波器保持对实际系统状态的跟踪[7-8]。增广状态β可视为模型参数,增广状态的跟踪偏差可视为模型参数失配,将强跟踪思想引入增广卡尔曼滤波器中,形成增广强跟踪卡尔曼滤波器,可以更好地对增广状态进行估计。增广强跟踪卡尔曼滤波器和普通增广卡尔曼滤波器(Augmented Extended Kalman Filter, AEKF)的实施过程相比,运算流程基本相同,只是在状态协方差预测过程中乘以一个时变的渐消矩阵LMD(k+1),借以实时改变增益矩阵。

P(k+1,k)=LMD(k+1)Φ(k+1,k)P(k)·

ΦΤ(k+1,k)+ΔtΓ(k)Q(k)ΓΤ(k)

LMD(k+1)= diag[λ1(k+1),…,λi(k+1),

…,λn(k+1)]i=1,2,…,n

确定时变渐消矩阵的一步算法为

V0(k+1) =E[γ(k+1)γT(k+1)]

N(k+1)=V0(k+1)-KaR(k+1)-

H(k+1,k)Γ(k)Q(k)ΓT(k)H(k+1,k)

M(k+1)=Φ(k+1,k)P(k)Φ(k+1,k)·

HT(k+1,k)H(k+1,k)

其中，ai的值可以依据系统扩展后的先验知识来确定,0<ρ≤1为遗忘因子,Kb≥1为弱化因子,γ(k)为第k步输出残差,n为扩展后的系统状态维数。

3 仿真结果及分析

依据1.1节中的卫星姿态确定系统的状态方程,将未知的干扰力矩项增广为状态矢量,则动力学姿态估计系统的状态方程可以改写为

对应到上面的增广卡尔曼滤波公式中有

f(xa(t),u(t))=

对于姿态确定系统的测量方程,则有

z(tk)=CS;h(x(tk),u(tk),β)=A(q)·CI

已知完备的卫星姿态确定系统状态方程和测量方程,便可以运用上面的增广卡尔曼滤波算法对星敏感器的测量数据进行滤波,得到卫星姿态的实时信息。干扰力矩、姿态角速率、姿态四元数信息都在卫星轨道坐标系中定义,星敏感器本体系坐标轴方向和卫星本体系坐标轴方向一致。三轴稳定小卫星的转动惯量矩阵为

参照文献[9-10],干扰力矩基本都是周期函数形式,采用如下形式来模拟干扰力矩

Td(t)=[ -Tdx0sin(ωφt),Tdy0sin(ωθt),

-Tdz0sin(ωψt)]

其中，Tdx0=Tdy0=Tdz0为1×10-5N·m。其中ωφ=6ωe、ωθ=4ωe、ωψ=8ωe,ωe为卫星的公转角速率,假定卫星在650km的圆轨道,则ωe为0.06148839356680(°)/s。滤波器初始状态为:

q0=[0.0,0.0,0.0,1.0]

ω0=[0.0,0.0,0.0]

Td=[0.0,0.0,0.0]

系统噪声为

E[w(t)wT(t)]=Q(t)=εI3×3

测量噪声为

E[v(tk)vT(tk)]=R(tk)=1×10-10I3×3

3.1 增广卡尔曼滤波器姿态估计结果

仿真所用干扰力矩如图1所示。图2、图3所示为采用不同的系统噪声(增广状态随机变化率)时,普通增广卡尔曼滤波器的干扰力矩和欧拉角估计误差。从图中可以看出,干扰力矩和欧拉角估计误差呈周期性变化,且其变化周期刚好与图1中显示的干扰力矩的变化周期一致。在干扰力矩的峰值处(变化率最小处)估计误差最小,相反在干扰力矩过零处(变化率最大处)估计误差最大。较大的系统噪声虽然可以抑制估计结果的振荡误差,但同时随机误差也会增大;采用较小的系统噪声,随机误差会减小,但估计结果会有很大的振荡误差。

图1 仿真所用的干扰力矩Fig.1 Perturbed moment for simulation

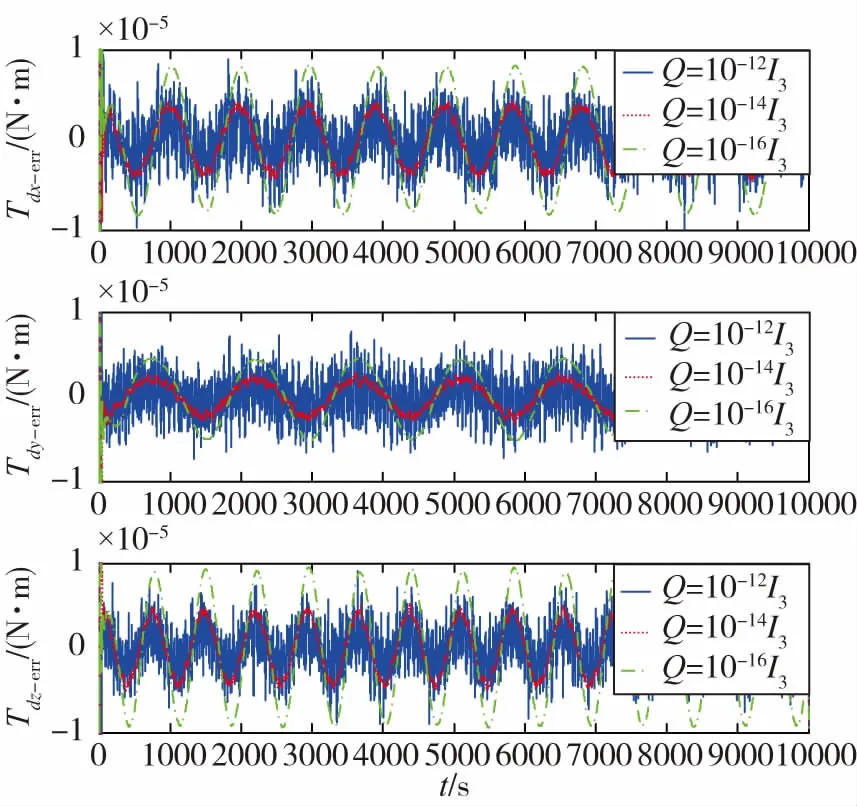
图2 AEKF干扰力矩估计误差Fig.2 Perturbed moment estimation error of AEKF

图3 AEKF欧拉角估计误差Fig.3 Eulerian angle estimation error of AEKF

图4、图5所示为增广强跟踪卡尔曼滤波器采用不同系统噪声时，干扰力矩和欧拉角估计误差与AEKF的估计结果一样,也呈周期性变化。但是ASTEKF结果受系统噪声的影响较小,且小系统噪声的估计不仅随机噪声较小,误差的偏离也得到了抑制。因此在使用ASTEKF时,不用担心过小的系统噪声会跟踪不上干扰力矩的变化带来的偏差。

图6、图7所示为增广自适应卡尔曼滤波器的干扰力矩和欧拉角估计误差,与AEKF不同,在估计误差的峰值处都呈现平台状,有效地抑制了峰值处干扰力矩变化带来的估计误差。

图4 ASTEKF干扰力矩估计误差Fig.4 Perturbed moment estimation error of ASTEKF

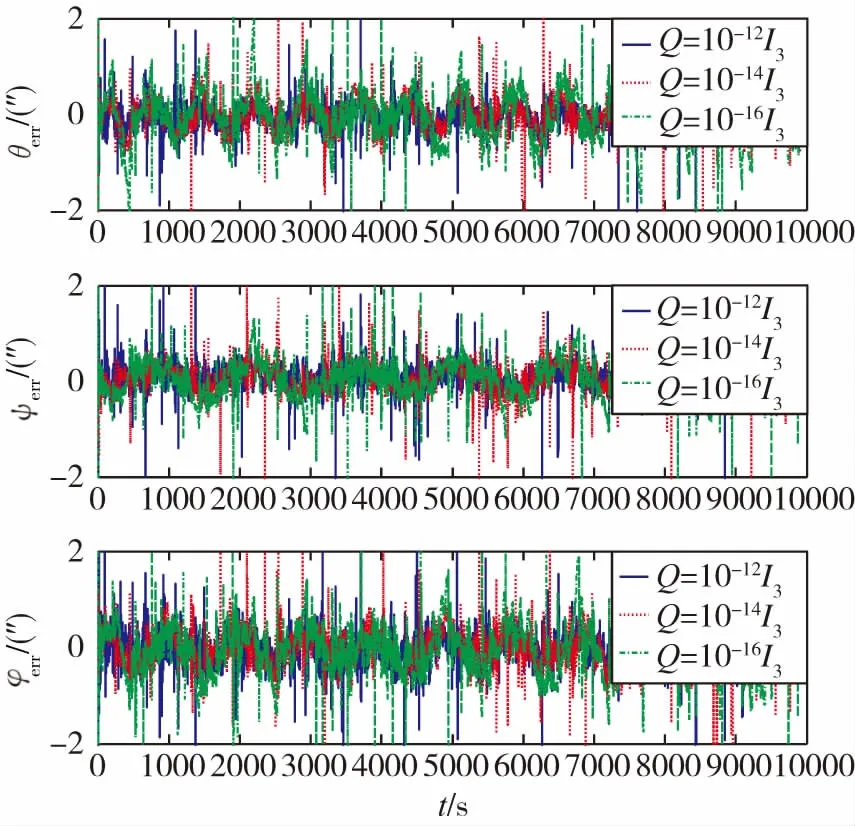
图5 ASTEKF欧拉角估计误差Fig.5 Eulerian angle estimation error of ASTEKF

图6 AAEKF干扰力矩估计误差Fig.6 Perturbed moment estimation error of AAEKF

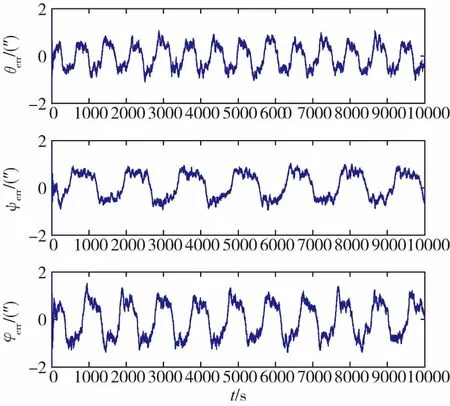
图7 AAEKF欧拉角估计误差Fig.7 Eulerian angle estimation error of AAEKF

图8、图9所示为三种算法估计结果的比较。对于AEKF而言,系统噪声不能太大,也不能太小,这里显示估计性能最好时的结果,此时Q=10-14·I3。对于ASTEKF而言,系统噪声尽可能地取小,这里选取Q=10-16I3。而AAEKF滤波过程中自适应调整系统噪声,因此无需选定一个系统噪声。从图中可以看出,AEKF和ASTEKF的最优性能与AAEKF的性能相当。三种滤波器的可操作性依次是AAEKF优于ASTEKF,ASTEKF又优于AEKF。

图8 三种算法干扰力矩估计误差Fig.8 Perturbed moment estimation error of three algorithms

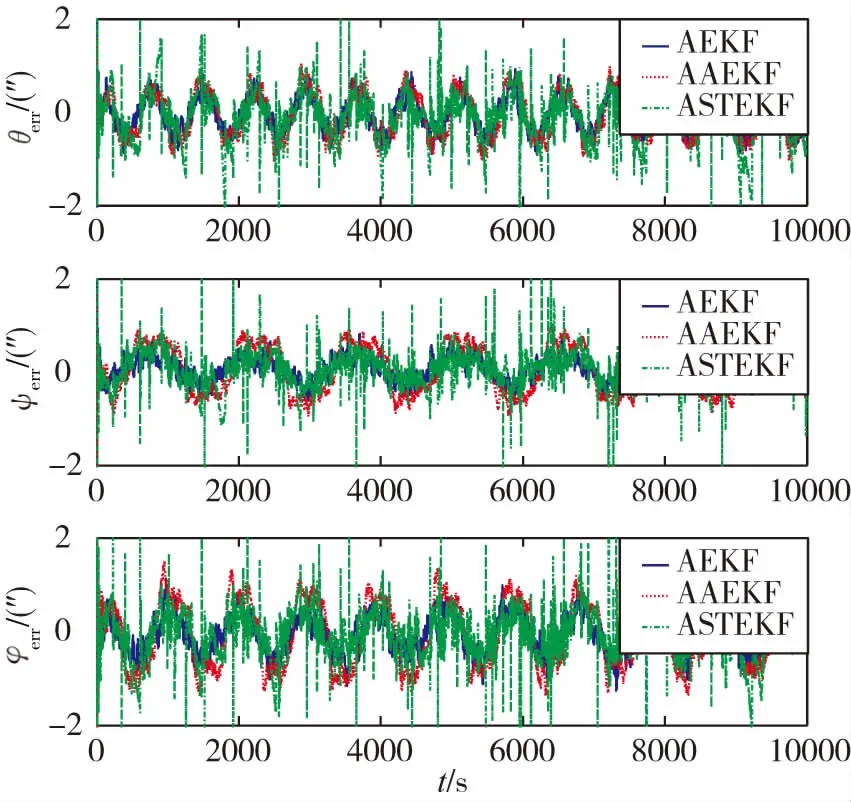
图9 三种算法欧拉角估计误差Fig.9 Eulerian angle estimation error of three algorithms

4 结论

对于AEKF而言,系统噪声的选取对滤波结果有着重要影响,必须对干扰力矩的实际情况有充分的了解才能选取合适的系统噪声,实用性较差；ASTEKF对系统噪声选取的依赖性较小,较小的系统噪声就可以跟踪上干扰力矩的变化,滤波结果的随机误差也得到了控制;AAEKF方法无需采用固定的系统噪声,通过实际的估计过程实时地给出系统噪声,同时抑制了估计结果随机误差和振荡型偏差,具有较强的实用性。

[1] Psiaki M L, Martel F, Pal P K.Three-axis attitude determination via Kalman filtering of magnetometer data[J].Journal of Guidance, 1990, 13(3): 506-514.

[2] George J, Crassidis J L.Sensitivity analysis of disturbance accommodating control with Kalman filter estimation[C]//Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit.Hilton Head, 2007.

[3] Lefferts E J, Markley F L, M.D.Shuster.Kalman Filtering for Spacecraft Attitude Estimation[J].Journal of Guidance Control & Dynamics, 1982, 5(4):536-542.

[4] Ljung L.Asymptotic behavior of the extended Kalman filter as a parameter estimator for linear systems[J].IEEE Transactions on Automatic Control, 1979, 24(1): 36-50.

[5] 蔡金狮.飞行器系统参数辨识学[M].北京:国防工业出版社,2003.

[6] Merwe R V D.Sigma-point Kalman filters for probabilistic inference in dynamic state-space models[D].University of Stellenbosch, 2004.

[7] 周东华,序裕庚,张钟俊.一种带多重次优渐消因子的扩展卡尔曼滤波器[J].自动化学报,1991,17(6):689-695.

[8] 周东华,叶银忠.现代故障诊断与容错控制[M].北京:清华大学出版社,2000.

[9] 屠善澄.卫星姿态动力学与控制[M].北京:中国宇航出版社,1998.

[10] 章仁为.卫星轨道姿态动力学与控制[M].北京:北京航空航天大学出版社,1998.