单兵导航多传感器信息融合自适应滤波算法

，， ，，

(1.陆军装甲兵学院 兵器与控制系，北京 100072; 2.清华大学 精密仪器系，北京 100084)

0 引言

单兵导航，主要是为士兵、警察、消防员等单兵在徒步执行作战任务时提供定位和导航服务，单兵的方位信息、位置信息是单兵作战的必备信息要素，直接关系到作战的规划、指挥、执行及最终的胜负[1-3]。在卫星信号无法到达或者被拒止的情况下，迫切需要单兵导航或者行人导航系统具有自主定位导航的能力，而且要求体积小、质量小、功耗低、可便携性强。

基于足绑式惯性导航系统的单兵导航系统，主要特征是通过将MEMS惯性传感器组成的IMU固定于足部，构成足绑式惯性导航系统[4-5]。惯性导航系统(Inertial Navigation System, INS)是一种重要的自主导航系统，它建立在牛顿经典力学定律的基础之上，利用陀螺和加速度计提供的测量数据确定所在运载体的位置[6-7]。惯性导航的精度受限于传感器精度，特别是对于MEMS惯性传感器，其误差发散非常快，低精度的INS在没有约束的情况下无法单独使用。单兵在步行时，足部的动作具有一定的规律，如足部在落地时处于相对静止状态，可以在足部落地静止时对足绑式INS进行零速修正(Zero Velocity Update，ZUPT)，限制INS误差的增长[8-10]。除ZUPT外，还可以利用磁强计、气压高度计、多普勒雷达等其他传感器信息对INS的误差进行修正。

单兵导航时徒步行走的步态不断变化，包括慢速步行、快速步行、慢跑、快跑、上楼、下楼、上坡、下坡等多种步态模式，每种步态模式下进行ZUPT和多传感器融合滤波时，实际滤波器量测噪声不同，如果采用相同的量测噪声进行滤波，估计值不能达到最优，严重情况下将引起滤波器发散。滤波器长时间运行后协方差矩阵P和滤波增益矩阵K逐渐收敛趋于稳态，量测新息的修正作用将非常小，随着时间增加，特别是在系统模型、量测模型不准的情况下，滤波器将不能快速有效地利用零速和其他传感器信息对足绑式INS的误差进行约束。所以，为保证长时间导航情况下滤波器能够快速有效的工作，需要抑制滤波发散，减弱滤波增益矩阵K的收敛速度，提升当前量测新息对状态变量的修正作用。

多传感器信息融合可采用Kalman滤波器，为适应多传感器融合单兵导航的需求，Kalman滤波器需要进行优化改进，一方面Kalman滤波器的量测噪声要能够自适应调整，以适应不同步态的量测噪声特点；另一方面为充分利用外部观测量信息，在进行滤波时，需要提升当前量测新息对状态变量的修正作用。为此，本文设计了一种自适应滤波算法进行单兵导航多传感器信息融合。

1 单兵导航多传感器融合误差模型

1.1 误差传递模型

对于足绑式INS，系统状态模型是非线性模型，所以普通线性Kalman滤波器无法使用，而足绑式INS的误差状态模型可近似为线性模型[11]。所以在足绑式INS中，可采用线性Kalman滤波器对系统误差状态变量进行估计，当估计出误差状态变量后，再对足绑式INS的姿态、速度和位置进行反馈校正。为保证误差状态模型的线性特性，误差反馈校准采用实时校正模式，对每次滤波估计值均进行反馈校正。

足绑式INS误差传递模型的状态变量设计为15维，如下

x=[ δθδγδψδVNδVEδVDδLδλδh

(1)

对基于足绑式INS的单兵导航系统，由于1/(RM+h)2和1/(RN+h)2的量级很小，而且高度通道有气压高度计约束，高度误差δh较小，所以可简化误差状态方程，提高单兵导航算法的实时性，简化后的足绑式INS误差状态方程如式(2)～式(10)所示[12]。

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

将式(2)～式(12)等系统误差状态方程写成在原点附近的雅克比矩阵形式，如式(13)～式(19)所示。

(13)

(14)

其中：

(15)

(16)

(17)

(18)

(19)

1.2 多传感器信息融合误差观测模型

基于足绑式INS的多传感器融合单兵导航系统，其外部观测量主要有虚拟零速、磁航向、气压高度、GNSS经纬度等，在同一时刻，可能只有其中一部分观测量有效，在实际使用时，可实时调整观测方程和观测矩阵以适应不同的观测量。本文将采用磁航向和虚拟零速作为观测量，如式(20)所示。

Z=[δYδVNδVEδVD]T

(20)

利用足绑式INS的计算结果减去外部观测量，得到误差状态方程的直接观测量：

(21)

其中，YNav和Ymag分别为INS和磁强计输出的偏航角，VN_Nav、VE_Nav和VD_Nav分别为INS输出的北东地速度。

由观测量可得到系统观测方程的观测矩阵H为一4×15维的常量矩阵，如下

(22)

2 基于Kalman滤波的误差状态估计

2.1 状态方程离散化

足绑式INS的误差状态模型离散化后，其状态方程和观测方程为[11]：

(23)

其中状态误差方程可表示为

Xk=(I+AΔt)Xk-1+Wk-1

(24)

其中，Δt为滤波周期，Φk，k-1为15×15维矩阵，如式(25)所示。

Φk,k-1=

图9为弹丸前定心部受力曲线，由曲线可以看出，就总体趋势而言，高温未磨损身管弹丸前定心部受力较其他2种工况较大，但弹丸前定心部在磨损身管内的受力个别时间点上较大，最大值约为26 kN，而未磨损身管的弹丸前定心部受力最大值约为145 kN。由于弹丸与身管发生了瞬间碰撞产生的，在动态作用下，由于材料的变形与屈服是一个缓慢过程，因此较大的瞬间力不会对弹丸结构产生破坏。但是，弹丸的横向和径向碰撞对装药的设计有一定的影响。

(25)

式中，Xk为系统的n维状态向量，Zk为系统的m维观测向量，Wk为n维过程噪声序列，Vk为m维观测噪声序列，Φk，k-1为n×n维的状态转移矩阵，Hk为m×n维观测矩阵。

系统过程噪声和观测噪声的统计特性如下：

(26)

其中，Qk为过程噪声方差矩阵，Rk为量测噪声方差矩阵，δkj为Kronecker-δ函数。

2.2 Kalman滤波估计及反馈校正

足绑式INS的误差状态模型是线性模型，采用线性Kalman滤波器作为多传感器辅助单兵导航的多源信息融合滤波器。Kalman滤波器估计结果可表示为[13]：

Kalman滤波器是针对线性系统的最优滤波器，INS误差状态方程必须工作在小误差状态时才能满足线性条件。对于足绑式INS采用的MEMS惯性传感器，其随机误差较大，INS的误差发散较快，所以本文采用实时反馈校正的模式。利用滤波器估计结果对足绑式INS进行实时反馈校正，使误差状态始终保持小量，减小系统的非线性误差，避免滤波器发散。反馈校正公式如下：

(28)

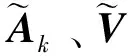
3 衰减记忆新息自适应Kalman滤波

学者A.P.Sage和G.W.Husa于1969年提出了一种自适应Kalman滤波算法，可以在进行状态估计时利用量测输出在线估计出系统的噪声参数，即Sage-Husa自适应Kalman滤波[14]。但这种算法是利用全部新息进行量测噪声的计算，当实际量测噪声发生快速变化时，如在单兵导航中不断改变步态模式，量测噪声不能反映当前真实的噪声情况。所以本文采用新息自适应滤波算法[13]，量测噪声矩阵主要根据当前一段时间内的量测新息进行计算，可以使量测噪声始终反映当前的量测噪声变化。虽然通过新息自适应滤波可以得到比较准确的量测噪声，但是由于系统模型存在误差，滤波器仍然可能发散，所以在新息自适应滤波的基础上同时采用衰减记忆滤波算法，衰减过去旧的量测新息，提高当前量测新息的比重，与新息自适应滤波算法组成衰减记忆新息自适应Kalman滤波算法。

(29)

理想状态下的新息为零均值白噪声，滤波器达到正常工作稳态时，其协方差阵如式(30)所示。

(30)

量测新息协方差矩阵Ak的估计值可采用一段滑动窗口内的量测新息进行估算，对于足绑式INS，滑动窗口的选取范围是落地ZUPT期间，如式(31)所示。

(31)

由式(30)可得量测方差矩阵R的估计值为

(32)

(33)

在新息自适应滤波的基础上引入衰减记忆滤波，其基本思想是加大新量测数据的作用，减小陈旧数据的影响，这样可以更加有效地利用外部观测信息对足绑式INS进行误差约束。

(34)

综合式(32)～式(34)与Kalman基本方程式(27)，可得到衰减记忆新息自适应Kalman滤波器表达式，如式(35)所示。

(35)

4 单兵导航实验验证

为验证本文提出的单兵导航自适应滤波算法的有效性，在某操场上进行足绑式INS单兵导航实验。绕操场行走，起点和终点重合，在行走的同时利用GPS模块记录行走轨迹。图1所示为实验时徒步行走轨迹，不同于一般的标准操场，它拥有一个方形的跑道，总距离约460m。

图1 实验时徒步行走轨迹Fig.1 Walking track

实验验证采用的IMU为ADI公司生产的MEMS IMU模块，型号为ADIS16488；该模块集成了三轴陀螺、三轴加速度计、三轴磁强计和气压高度计。实验时设计了专用的数据采集电路，将IMU固定于脚面，手持笔记本电脑，通过串口实时采集并保存IMU输出原始数据和GPS模块坐标信息。数据采集频率为200Hz。数据处理和算法实现通过离线方式在Matlab中计算完成。足绑式INS的初始坐标由GPS给定，初始方向由磁强计给定，三轴磁强计、三轴陀螺和三轴加速度计提前在实验室进行了校准，在实验过程中利用磁强计对航向角误差进行约束。

实验采集了3组整圈徒步单兵导航数据，第一组和第二组数据为匀速步行单兵导航数据，第三组为步行、跑步混合单兵导航数据。

为验证本文提出的衰减记忆新息自适应Kalman滤波器算法，在单兵导航多源信息融合基本算法架构的基础上，对3组数据分别采用普通Kalman滤波器和自适应Kalman滤波器进行处理，比较3组数据的单兵导航终点误差，由于起点和终点重合，起点和终点坐标之差即为单兵导航终点误差。图2～图7所示为3组数据导航轨迹与GPS轨迹比较图，单兵导航轨迹起点与GPS轨迹起点一致。表1所示为3组导航数据采用不同滤波器时的终点误差统计。

图2 第一组导航轨迹图(普通滤波)Fig.2 Navigation track of the first group(normal filter)

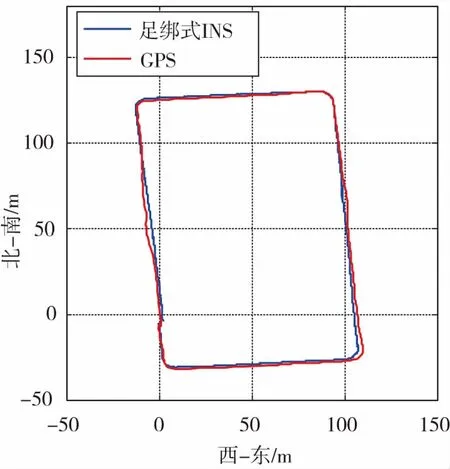
图3 第一组导航轨迹图(自适应滤波)Fig.3 Navigation track of the first group(adaptive filtering)

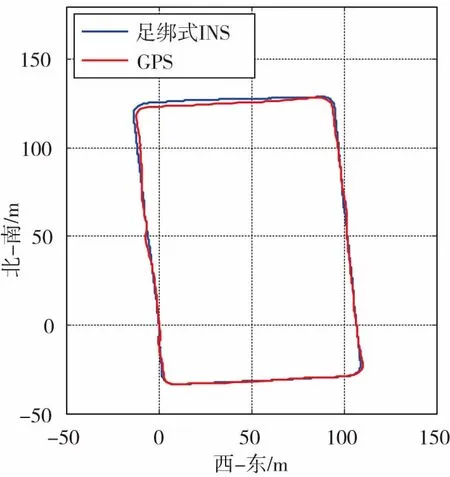
图4 第二组导航轨迹图(普通滤波)Fig.4 Navigation track of the second group(normal filter)

图5 第二组导航轨迹图(自适应滤波)Fig.5 Navigation track of the second group(adaptive filtering)

图6 第三组导航轨迹图(普通滤波)Fig.6 Navigation track of the third group(normal filter)

图7 第三组导航轨迹图(自适应滤波)Fig.7 Navigation track of the third group(adaptive filter)

滤波类型类别第一组匀速步行第二组匀速步行第三组步行跑步混合普通Kalman滤波东向误差/m056248-649北向误差/m009035835自适应Kalman滤波东向误差/m-011141206北向误差/m103091247误差占总距离比例022%031%053%

5 结论

通过比较采用不同滤波器时的单兵导航结果，匀速步行时使用普通Kalman滤波和自适应Kalman滤波导航误差区别不大，单兵导航的轨迹与GPS轨迹基本重合，由表1可知，单兵导航的误差可控制在2m左右，约占总距离的0.5%，验证了单兵导航多源信息融合基础算法的有效性。对于第三组步行和跑步混合的单兵导航数据，采用衰减记忆新息自适应Kalman滤波器后，单兵导航的终点误差比普通Kalman滤波器大幅减小。自适应滤波器可自适应估计混合步态时滤波器的量测噪声，并能更好地利用量测新息，滤波器估计结果更加准确，实验验证了本文所提出的单兵导航多传感器信息融合自适应滤波算法的有效性。

[1] Harle R. A survey of indoor inertial positioning systems for pedestrians[J].IEEE Communications Surveys & Tutorials, 2013, 15(3):1281-1293.

[2] 李石兵, 龚贻华, 郭小荣, 等. 行人导航技术及携行式单兵导航应用[C]//第三届中国指挥控制大会. 北京, 2015.

[3] Foxlin E. Pedestrian tracking with SHOE-mounted inertial sensors[J]. IEEE Computer Graphics and Applications, 2005, 25(6): 38-46.

[4] Godha S， Lachapelle G. Foot mounted inertial system for pedestrian navigation[J]. Measurement Science & Technolgogy，2008,,19(7):1-9.

[5] Feliz A R，Zalama C E, Gómez G J. Pedestrian tracking using inertial sensors[J]. Journal of Physical Agents, 2009,3(1):35-43.

[6] 高钟毓. 惯性导航系统技术[M]. 北京: 清华大学出版社, 2012.

[7] 秦永元. 惯性导航(第二版)[M].北京: 科学出版社, 2013.

[8] Skog I, Nilsson J O, Handel P. Evaluation of zero-velocity detectors for foot-mounted inertial navigation systems[C]//2010 International Conference on Indoor Positioning and Indoor Navigation (IPIN). Zurich, 2010.

[9] Skog I,Handel P,Nilsson J O， et al. Zero-velocity detection-an algorithm evaluation[J]. IEEE Transactions on Biomedical Engineering, 2010,57(11): 2657-2666.

[10] Fourati H. Heterogeneous data fusion algorithm for pedestrian navigation via foot-mounted inertial measurement unit and complementary filter[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(1): 221-229.

[11] 郭美凤，林思敏，周斌，等. MINS/GPS一体化紧组合导航系统[J]. 中国惯性技术学报, 2011，19(2): 214-219.

[12] 严恭敏. 车载自主定位定向系统研究[D]. 西安：西北工业大学, 2006.

[13] 秦永元. 卡尔曼滤波与组合导航原理(第二版)[M]. 北京: 科学出版社, 2012.

[14] Sage A P,Husa G W.Adaptive filtering with unknown prior statistics[C]//Proceedings of Joint Automatic Control Conference, 1969.