湍流下目标散射回波时域起伏特征研究

孙华燕,单聪淼,郑勇辉

(1.装备学院,北京 101416；2.卫星通信中心,北京 100094)

1 引 言

大气湍流效应是对激光主动探测系统进行远场侦察探测与目标识别作业时探测激光大气传输最主要的非线性影响因素之一[1-3],光学目标与漫反射体相比具有较强的激光原路返回特性,利用回波能量的差异可以对漫反射体和光学目标进行区分[4-6],然而在实际应用中光学目标由于受口径、激光入射角等影响,其回波能量特征有时并不明显,“猫眼”目标、角反射器等光学目标的分类识别也无法单纯依靠回波能量作出判决,新的目标分类依据有待研究。

现有理论和实验研究表明[7-9],在相同的湍流大气条件下,不同目标激光散射回波的起伏特性是有差异的。回波起伏的统计特性与目标的散射特性有关,某些散射体能放大光波形变,而另一些则对光波形变有补偿作用。因此,研究一定湍流条件下特定目标的激光散射回波起伏特性,建立回波起伏与目标散射特性间的映射关系,对于激光主动探测来说是很有意义的。

为研究不同目标激光散射回波在弱湍流影响下的差异,以高斯光束为模型,利用Rytov近似法和广义Huygens-Fresnel原理,推导得到了适用于不同目标的原路返回处的场分布。采用高重频激光系统对一定距离处的漫反射体、“猫眼”目标和角反射器做了回波探测实验,测得回波的时间起伏信息,通过数据处理与分析,得到了回波的起伏特征,并对不同目标的特征差异进行了比较分析。得到的结果为激光主动探测应用的目标分类识别提供了重要依据。

2 理论分析

针对湍流下目标散射回波时域起伏特征进行研究,需要先对湍流环境下不同目标的散射回波的光强分布进行推导分析。图1为大气湍流中高斯光束的双程传输模型。将此传输过程分解为三个变换过程:入射传输过程、目标反射过程及反射传输过程。依次对每个传输过程进行分析,其中l0为湍流内尺度,L0为湍流外尺度。

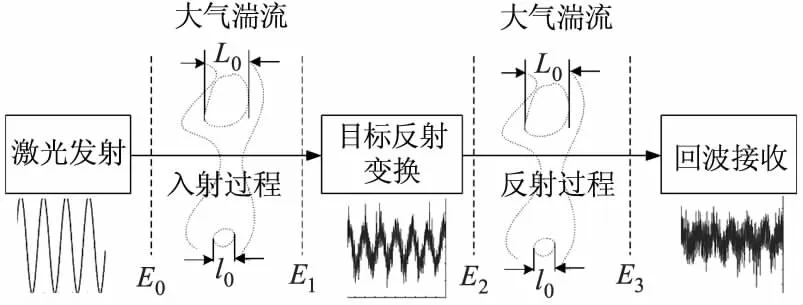
图1 大气湍流中高斯光束的双程传输模型

激光发射系统处的高斯光束的场分布为[10]:

(1)

式中,F0和ω0分别为发射系统处的波前曲率半径和波束半径。

利用Rytov近似法和广义Huygens-Fresnel原理,可以得到高斯光束在大气湍流中传输到距离为L处的场分布为:

(2)

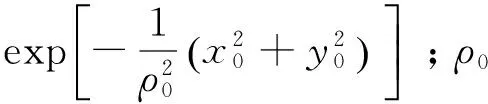
(3)

高斯光束在大气湍流中传输距离L到达有限口径的目标处时,由于目标内部光程远小于传输距离,故可将光束在目标内部的传输视为真空传输,利用广义Huygens-Fresnel衍射原理,可以得到高斯光束从目标反射的场分布为:

(4)

式中,(x2,y2)为经目标反射后目标平面上的二维坐标；F(x1,y1)为有限尺寸目标的孔径滤波函数,此函数与目标性质有关。

再次利用Rytov近似法和广义Huygens-Fresnel衍射原理,则原路返回的高斯光束在接收平面处的场分布为:

E3(x3,y3,L)=

(5)

式(5)描述了高斯光束在大气湍流中经过目标的双程传输过程,采用高斯光束进行模型建立是为了使分析具有一般性。由于不同目标的孔径滤波函数不同,在具体分析时只需要将对应目标的孔径滤波函数代入即可。

图2 不同目标的回波归一化标准差

3 湍流下目标回波采集实验方案

回波采集实验示意图如图3所示,用高重频激光系统在夜间、大气微扰动条件下对1 km外的漫反射面、“猫眼”目标以及角反射器做连续探测,其中系统指标:激光器输出波长为532 nm,发散角6 mrad,重复频率为10 kHz,功率为40 W,脉宽为90 ns,PMT 响应波长185～900 nm,阴极灵敏度74 mV/W,PMT后面接500 MHz采样率量程可调的8位高速数字采集卡,对回波数据做采集和存储。回波采集的软件操作界面如图4所示。

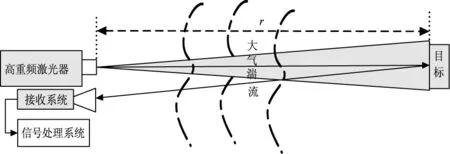
图3 目标回波起伏特征实验示意图

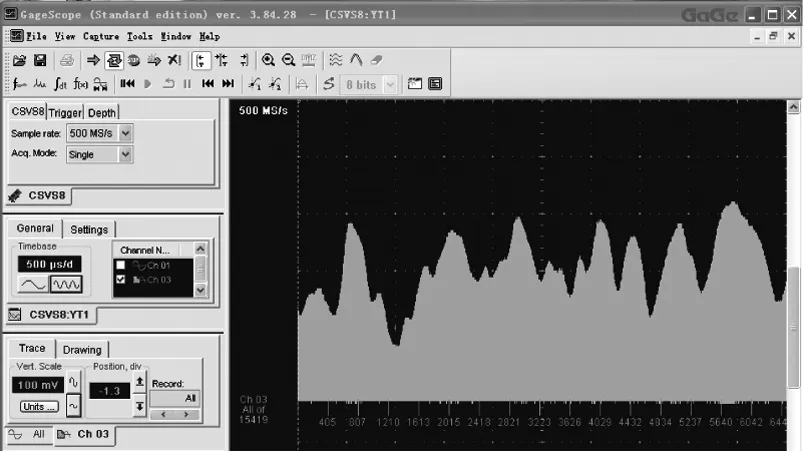
图4 回波采集软件界面

图4中所示的数据即为实验中获取的连续多个脉冲的起伏信息,提取这些脉冲的峰值,得到了连续多个脉冲的峰值序列,该信息便反映了激光受大气衰减影响的时域能量起伏,对连续峰值序列做时域和谱分析,提取不同目标的回波特征。

4 实验结果与分析

通过对实验数据的分析,得到了漫反射面、猫眼、角反射器之间的回波起伏差异。

4.1 漫反射面与光学目标回波起伏差异与分析

除去回波能量大小的明显差异外,漫反射面与光学目标的回波差异主要表现为回波起伏强度的差异,对回波数据做归一化处理,求得漫反射面与不同口径的猫眼和角反射器回波起伏标准差如表1所示,可以看出漫反射面的回波起伏标准差明显低于光学目标。另外,由表1还可以得出,目标的口径对回波起伏影响也是存在的,整体来讲,目标口径越小,回波起伏越强。

表1 漫反射面与光学目标回波归一化起伏标准差

根据激光波束在湍流大气中的传输理论,在近距离、弱湍流条件下,激光闪烁的对数强度方差可表示为:

(6)

式中,C0是与光束相关的系数,对于球面波束与平面波束,C0分别取0.496和1.24;r是激光传输距离;K0为与湍流外尺度对应的空间波数;Cn2为大气折射率结构常数。

漫反射回波可近似为球面波,光学目标散射回波因其具有较好的原路返回特性可认为是平面波,由式(6)知,相同条件下的漫反射回波起伏标准差应小于光学目标的回波起伏标准差,另外,现有理论表明,闪烁效应激光的调制作用与激光源的发射口径有光,通常大的发射口径光学天线有较小的调制度,因此,目标口径对返程回波的闪烁影响可由此理论进行分析,同等条件下口径大的目标回波起伏强度应弱于口径小的目标回波。表1中的数据结果与此分析是一致的。

4.2 猫眼目标与角反射器回波起伏差异与分析

经过归一化处理与功率谱估计,得到角反射器与后向散射角不同的两种“猫眼”回波峰值起伏功率谱如图5所示,可以看出,两者在高频段的数值存在明显的差异,“猫眼”的平均谱值比角反射器的平均谱值高约5 dB,说明“猫眼”回波的峰值起伏相比于角反射有更多的细节信息。

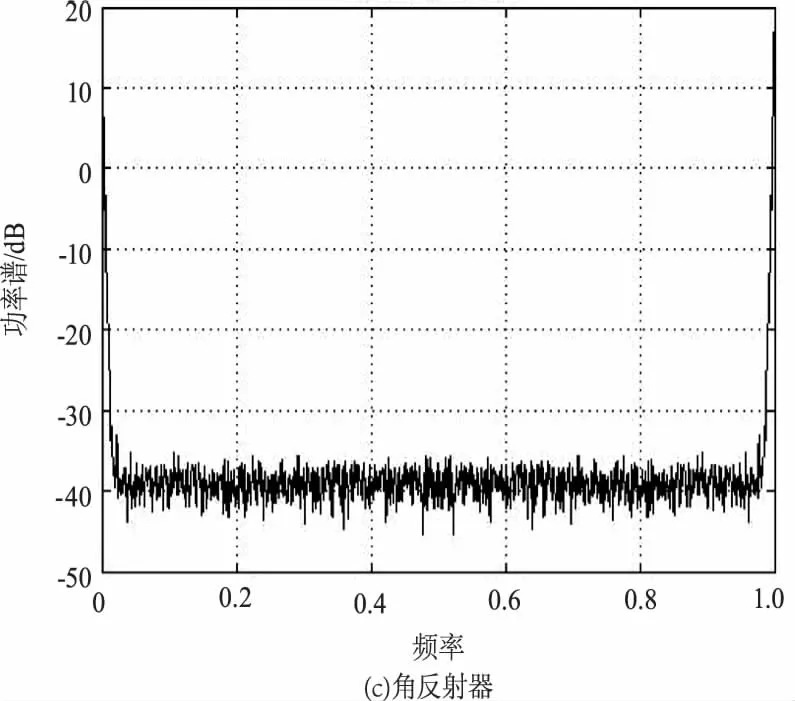
图5 角反射器与猫眼回波峰值起伏功率谱

为提取此特征,定义参数:

(7)

取a=100,b=1000,得到不同激光器输入电流下的回波功率谱γ值如图6所示(J:角反射器,M:大后向散射角“猫眼”,XM:小后向散射角“猫眼”)。

图6 不同输入电流下的回波功率谱γ值

研究回波起伏的高频信息,可以借助于“冻结湍流”假设(又称Taylor假设)进行分析,该假设认为,在光束传输的极短时间内,湍流折射率分布随时间的变化可以忽略,因此,高频起伏信息可以认为是探测系统稳定度的表征,“猫眼”散射的原路返回特性弱于角反射器,因此系统的“细微扰动”对“猫眼回波”的影响也会强于对角反射器的影响,反映到频谱中则会表现为“猫眼”回波起伏的高频段谱值高于角反射器回波。

4.3 猫眼离焦量对回波起伏的影响

猫眼离焦量的大小反映在散射激光上即为后向散射角的大小,在功率谱的低频段内,比较后向散射角不同的两种“猫眼”目标回波峰值起伏如图7所示,从左至右分别为激光器输入电流为16 A、17 A、18 A时的四组回波峰值起伏功率谱图,其中XM系列曲线为小后向散射角“猫眼”回波功率谱,M系列曲线为大后向散射角“猫眼 ”回波功率谱,由图可以看出,在0.005～0.01 Hz的频段内,两者存在着不同,大后向散射角“猫眼”的功率谱在此频段内的值小于小口径猫眼的值,两者一般相差几至十几分贝,说明大后向散射角“猫眼”回波,也即大离焦量“猫眼”回波在此频段内的起伏强度弱于小离焦量“猫眼”的回波峰值起伏。

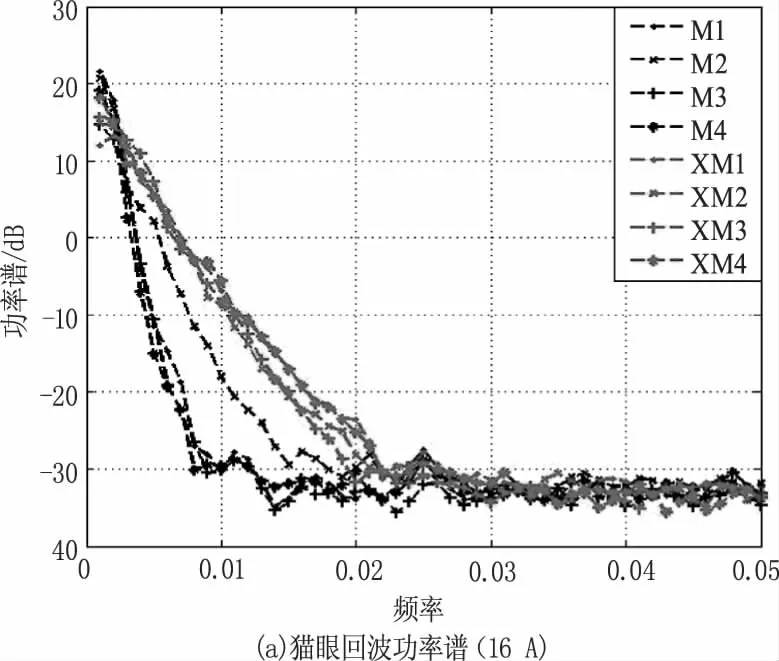
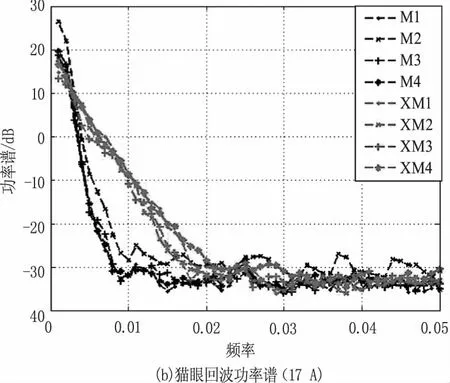
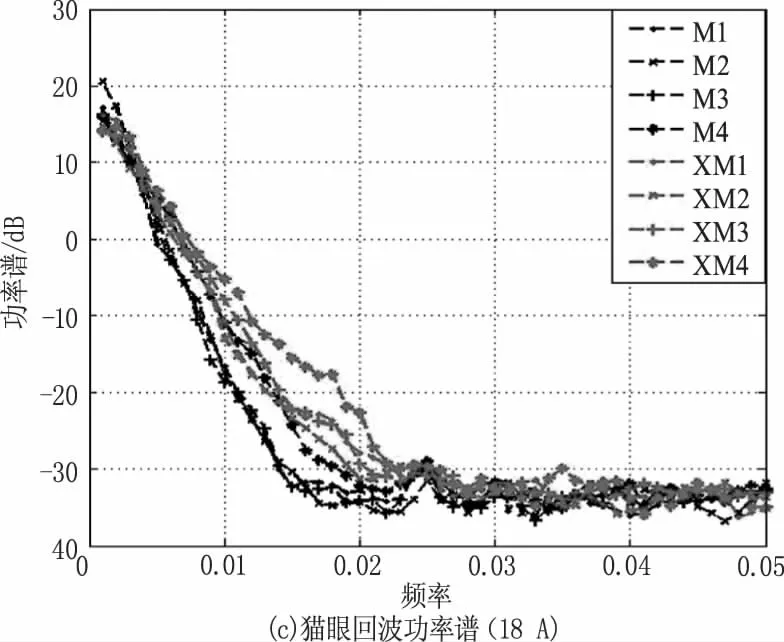
图7 角反射器与猫眼回波峰值起伏功率谱

定义参数:

(8)

a和b的值分别取为0.005和0.01,得到λ的值如图8所示。

如4.2节的分析,回波起伏的高频谱值可以认为是系统稳定度的表征,湍流的影响主要在回波的低频段,由图8可知,离焦量特征所处频段位于湍流影响的高频段,前面所述特征可描述为大离焦量“猫眼”的回波起伏受湍流影响的细节信息弱于小离焦量“猫眼”。

研究表明,离焦量对回波的影响除了发散角的不同之外,对回波光束的空间分布也有影响,非离焦情况下回波具有较好的空间相干性,有离焦量存在,空间相干性则会变弱,相干性好的光束能够快速跟随大气折射率结构常数的变化而化,而相干性差的光束不同路径上的干涉效应复杂,对大气折射率结构常数的变化起到了一定的时间平滑作用,丢失掉湍流起伏的一些细节信息,也因此有了如上特征。

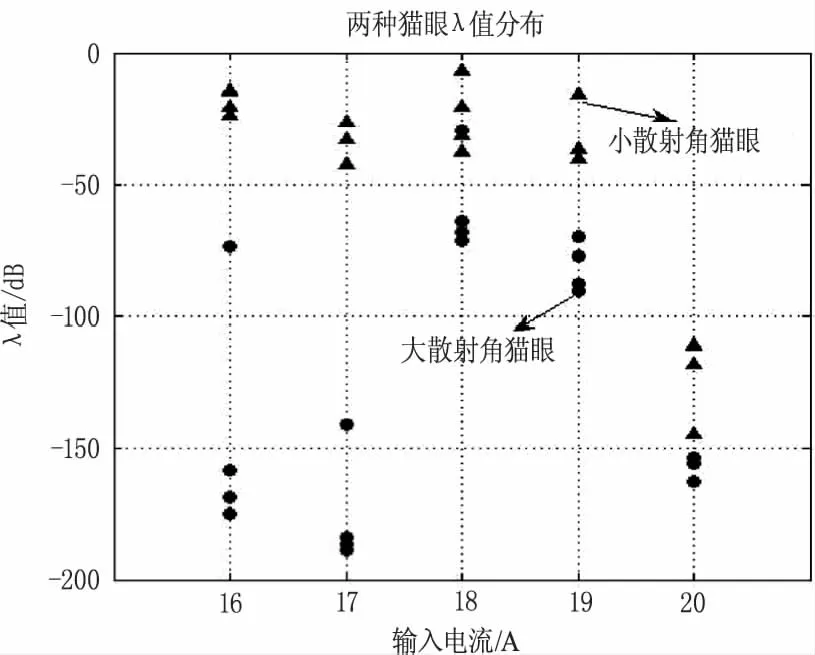
图8 猫眼回波λ值分布图

5 结 论

通过湍流下目标高重频激光回波峰值起伏实验和数据处理分析,得到了同等条件的弱湍流下漫反射面、角反射器和“猫眼”目标的散射激光回波在时域起伏上表现出的差异,并简单分析了产生此种差异的可能原因,为激光主动探测系统的目标分类识别提供了重要依据。

然而实际大气湍流对光束传播的影响较为复杂,不同大气条件,不同传输距离等因素对回波特征影响的分析还有待研究。另外,光束在远距离、强湍流条件下的传输规律将更为复杂,该条件下的回波特征分析尚待进一步探索。

[1] Alan M Whitman,Mark J Beran.Two-scale solution for atmospheric scintillation from a point source[J].J.Opt.Soc.Am.A,1993,5(5):735-737.

[2] Beran M J, Whitman A M.Scintillation index calculation using an altitude dependent structure constant[J].Appl.Opt.,1988,27(11),2178-2182.

[3] Andrew Forbes.Laser beam propagation in non-linearly absorbing media[J].SPIE,2006,6290:629003.

[4] Shi Jiaming, Wang Feng.Review of foreign army photoelectric countermeasure equipment[J].Modern military,2005,(10):40-42.(in Chinese)

时家明,王峰.国外陆军光电对抗装备综述[J].现代军事,2005,(10):40-42.

[5] LI Shuanggang, CHENG Yubao.Theoretical analysis on echo power of active laser reconnaissance based on“cat-eye”effect[J].Infrared and Laser Engineering,2006,35(sup.):80-83.(in Chinese)

李双刚,程玉宝.基于“猫眼”效应的激光回波功率理论分析[J].红外与激光工程,2006,35(增刊):80-83.

[6] HE Ting,NIU Yanxiong,ZHANG Peng,et al.Original analysis and influence of the focal shift on the retroreflected power of cat′s eye effect[J].Infrared and Laser Engineering,2012,41(11):2956-2960.(in Chinese)

和婷,牛燕雄,张鹏,等.光电系统离焦量对其猫眼效应回波功率的影响规律及原因分析[J].红外与激光工程,2012,41(11):2956-2960.

[7] SHAN Congmiao,SUN Huayan,ZHAO Yanzhong,et al.Analysis of cat-eye terminal echo flashing based on the modified Rytov method[J].Laser & Infrared,2013,43(8):876-880.(in Chinese)

单聪淼,孙华燕,赵延仲,等.猫眼终端回波闪烁效应分析[J].激光与红外,2013,43(8):876-880.

[8] Echo Scintillation Index affected by Cat-eye Target′s Caliber in FSO Communication[C].SPIE,2013.

[9] FAN Youchen,ZHAO Hongli,SUN Huayan,et al.Level set algorithm for the extraction of target contour under backscatter interference[J].Laser & Infrared,2015,45(5):589-594.(in Chinese)

范有臣,赵洪利,孙华燕,等.基于水平集算法后向散射的运动目标轮廓提取[J].激光与红外,2015,45(5):589-594.

[10] Ishimaru A.Wave propagation and scattering in random media[M].New York:Academic Press,1978.

[11] Cai Y J,Lin Q,Eyyuboglu H T,et al.Generalized tensor ABCD law for an elliptical Gaussian beam passing through an astigmatic optical system in turbulent atmosphere[J].Applied Physics B,2009,94(2):319-325.