对称型CJO代数的Groebner基
2018-01-29邱建军
邱 建 军
(岭南师范学院 数学与统计学院,广东 湛江 524048)
1 背景介绍
设Symn是n次对称群,H⊆Symn. 最近,Cedó, Jespers和Okniński[1-2]引入了一种新的数域k上的有限表示半群代数k[Sn(H)],
k[Sn(H)]=k〈x1,x2,…,xn∶xσ(1)xσ(2)…xσ(n)=x1x2…xn,σ∈H〉.
称代数k[Sn(H)]为Cedó-Jesper-Okniński代数, 简称为CJO代数.
另一方面, Groebner基理论[3-5]是上个世纪60到70年代发展起来的一个新的数学分支. 目前它在数学的各个领域, 特别是李代数, 结合代数, 群论, 半群理论, 计算代数和机器证明等方面都有广泛的应用.
本文将用Groebner 基理论来研究对称型CJO代数k[Sn(Symn)],得到了对称型CJO代数的一个Groebner基,从而利用C-D引理获得对称型CJO代数的一个线性基底.
2 Groebner基理论
在这一节, 我们简单介绍一下Groebner基理论的基本定义和结论.
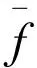
定义1.1[5]设f和g是k〈X〉的两个首1多项式.
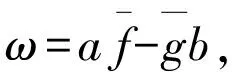
(f,g)ω=af-gb
为多项式f,g相对于ω的相交合成.
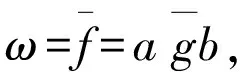
(f,g)ω=f-agb
为多项式f,g相对于ω的包含合成.
设S⊆k(X)是首1的多项式集, 则称合成(f,g)ω是S模平凡的, 如果
(f,g,)ω=∑αiaisibi,

如果S集中的所有多项式的合成都是模S平凡的, 则称S为k〈X〉的一个Groebner基.
定理1.2[5](C-D引理) 设S⊆k〈X〉是首1的多项式集, 则下面两个命题等价:
(I)S是k〈X〉的一个Groebner基;

3 对称型CJO代数的一个Groebner基
当H=Symn时, 称代数
k[Sn(Symn)]=k〈x1,x2,…,xn:xσ(1)xσ(2)…xσ(n)=x1x2…xn,σ∈Symn〉
为对称型CJO代数.
设X={x,i|1≤i≤n}, 其序“>”定义为xi>xj,如果i>j. 定义自由幺半群X*的序“>”为次数字典序.

设S是由下面的多项式组成的集合:

其中di(w1w2)表示w1w2中xi的个数.
引理2.1k[Sn(Symn)]=k〈X|S〉.
证明: 容易验证结论成立.
定理2.2S是k〈X〉的一个Groebner基.
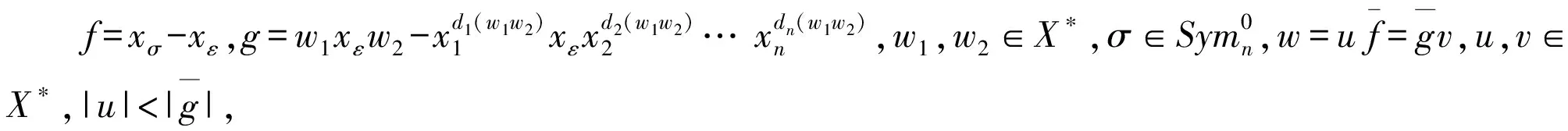
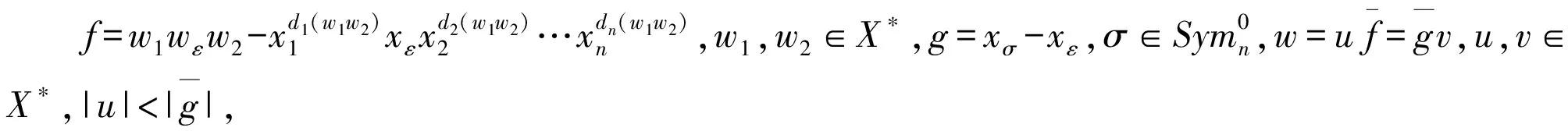
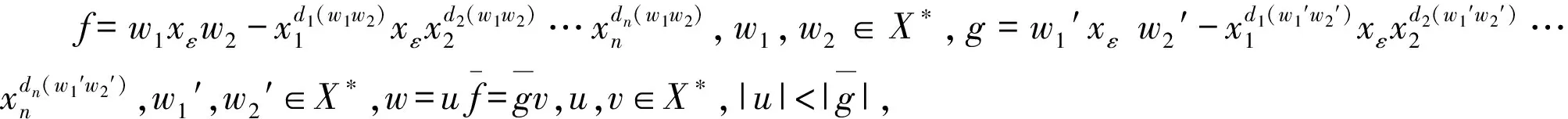

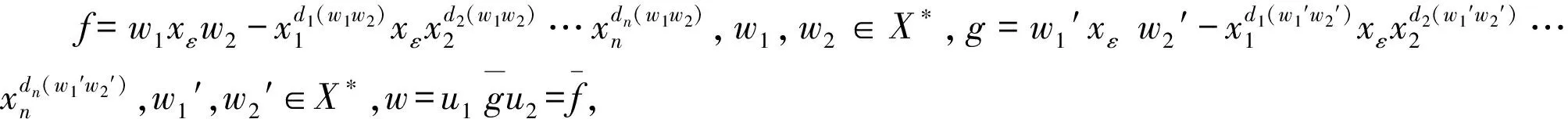
故而S是k〈X〉的一个Groebner基.
定理2.3集合
是对称型CJO代数k[Sn(Symn)]的一个线性基底.
证明: 由定理 2.3和定理 1.2可得结论成立.
[1] Cedó F, Jespers E , Okniński J. Finitely presented algebras and groups defined by permutation relations [J]. J. Pure App. Algebra, 2010, 214 (7): 1095-1102.
[2] Cedó F, Jespers E, Okniński J. Algebras and groups defined by permutation relations of alternating type [J]. J. Algebra, 2010, 324 (6): 1290-1313.
[3] Shirshov A I. Some algorithmic problem for Lie algebras [J]. Sibirsk. Mat. Z., 1962, 3 : 292-296.
[4] Buchberger B. An algorithm for finding a basis for the residue class ring of a zero-dimensional polynomial ideal [in German], Ph.D. thesis [C]. Austria: University of Innsbruck, 1965.
[5] Bokut L A. Imbeddings into simple associative algebras [J]. Algebra i Logika, 1976, 15: 117-142.
