基于CFD-DEM的柱形颗粒固定床反应器流场特性数值模拟

王凯莉,张亚新

新疆大学化学化工学院，新疆 乌鲁木齐 830046

固定床反应器被广泛应用于各种化工生产过程中，其结构多为圆柱形，内部床层由颗粒状催化剂和催化剂载体填充而成。对于球形颗粒填充床，国内外学者已进行深入的研究[1-5]，但在实际生产中，催化剂颗粒形状多为异形，如圆柱外齿轮形，七筋车轮形和四孔圆柱形等。现有的研究表明，催化剂颗粒形状是影响反应效果和操作条件的重要因素[6,7]，对固定床床层的流场特性有着极其重要的影响。Dixon[8]研究了颗粒形状对固定床空隙率的影响，得到球形、空心圆柱体和实心圆柱体的空隙率计算方程。董宝川[9]采用计算流体动力学（CFD）方法，模拟了固定床内部结构对流动性能的影响，认为球形比圆柱形颗粒堆积床层更加密实。Nemec等[10]研究了催化剂颗粒形状对填充床内的压降影响，认为Ergun方程只适用于预测球形颗粒填充床的压降。Yang等[11]研究了颗粒形状对结构填充床中的流动和热传递都有重要影响。虽然上述研究揭示了颗粒形状对床层流场特性的影响，但对于颗粒随机堆积固定床的数值模拟研究，大多局限于球形或颗粒形状的模型简化上，而且这些研究没有涉及柱形催化剂。本工作采用计算流体动力学-离散单元耦合法（CFD-DEM），通过DEM软件建立柱状颗粒实体随机堆积床层，而后与Fluent软件耦合计算，通过床层空隙率、压力场和速度场分布规律分析了不同管径和颗粒直径的比值（直径比）对流场特性影响，基于此方法的模拟结果更加接近生产实际，为反应器结构优化提供了理论依据。

1 计算模型

1.1 流体相控制方程

CFD-DEM耦合模型中气相控制方程主要有A模型、B模型和C模型，具体可参见文献[12]。本工作采用A模型描述颗粒和流体相的耦合作用，流体相控制方程为：

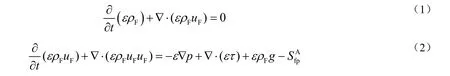
式中：ε为计算网格内的流体空隙率；ρF为流体密度，kg/m3；uF为流体速率，m/s；τ为流体粘性应力张量，Pa；g为重力加速度，m/s2；为两相动量交换原相，即：

1.2 流体-颗粒作用力

采用Free-stream曳力公式计算[13]，即：

式中：ρ为流体密度，kg/m3；A为柱状颗粒等效体积球的截面积，m2；ν为颗粒与流体之间的相对速度，m/s；cD为阻力系数，其具体计算公式为：

式中：Re为流体雷诺数；α为计算流体网格单元的自由体积，m3；L为柱形颗粒等效体积球的接触直径，m；η为流体粘度，Pa·s。

2 基于CFD-DEM的床层流场特性数值模拟

2.1 模型建立

2.1.1 快速填充柱形颗粒模型

以新疆伊犁某企业实际所用催化剂颗粒为例，统计测量了七孔柱形催化剂颗粒的平均直径（D）为10.26 mm、平均高度（H）为5.45 mm、平均孔直径（d）为2.34 mm。运用DEM软件，以球形为基础单元进行填充构建柱形颗粒模型。利用workbench平台先建立如图1（a）所示的柱形颗粒模型，再通过 fluent网格确定颗粒生成点，借用UDF（User Defined Function）把这些生成点输出，最后用DEM的颗粒工程API按照已获得的生成点生成颗粒。此次共填充414颗直径为1.5 mm的基本球单元颗粒形成柱状催化剂模型，见图1（b）。

图1 柱形催化剂颗粒模拟计算模型Fig.1 Simulation model of cylindrical catalyst particle

2.1.2 固定床反应器结构尺寸参数

图2为固定床反应器结构模型，管长为240 mm，床层高度为150 mm，内径为103 mm。

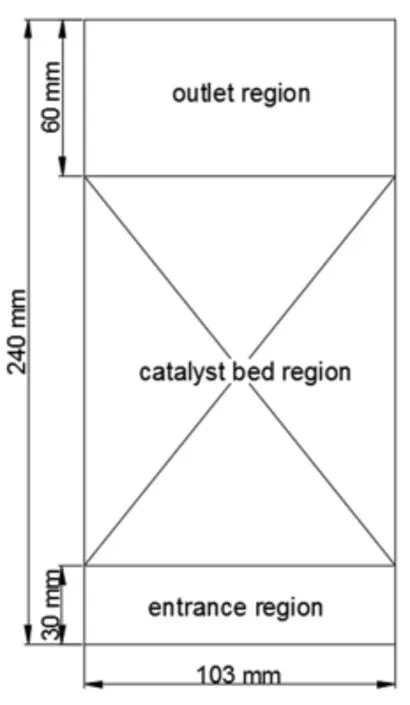
图2 固定床反应器几何模型Fig.2 Geometry model of fixed bed reactor

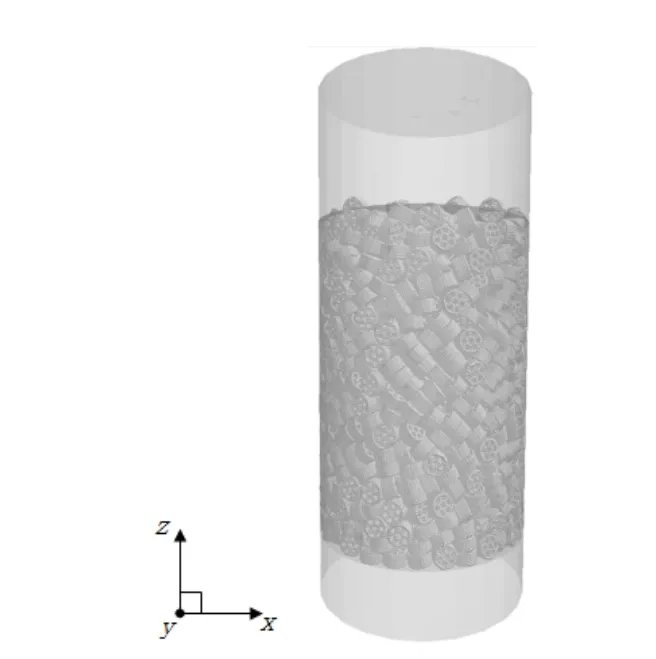
图3 固定床床层模拟计算模型Fig.3 Simulated computational model of fixed bed reactor

2.1.3 固定床柱状催化剂床层生成

在完成柱状催化剂颗粒单元模型的建立后，利用DEM中的Geometry面板中设置颗粒工厂几何特征。柱状催化剂颗粒采用动态生成的方法，并依据反应器直径比设置合适的颗粒总数和生成速率。柱状颗粒在自身重力作用下随机下落堆积生成颗粒床层，使颗粒填满整个计算域。建立完成后的颗粒床层模型如图3所示。

2.2 计算工具条件设置

2.2.1 DEM设置

催化剂堆积颗粒采用粗糙毛玻璃材料，固定床的壁面采用碳钢材料。具体的参数设置如下：催化剂颗粒泊松比为 0.25，密度为 2 456 kg/m3，剪切模量为 2.2×108Pa。颗粒碰撞模型采用Hertz-Mindlin(no-slip)模型，颗粒与颗粒恢复系数为0.5，颗粒与颗粒静摩擦系数为0.154，颗粒与颗粒滚动摩擦系数为0.1。壁面泊松比为0.3，密度为7 800 kg/m3，剪切模量为7×108Pa，壁面与颗粒碰撞恢复系数为0.3，壁面与颗粒静摩擦系数为0.154，壁面与颗粒动摩擦系数为0.1。

2.2.2 Fluent设置

在Fluent边界条件设置中，计算模型选用k-ε湍流模型，模拟为瞬态，入口条件设置为速度入口，速率为1 m/s，进口与床层之间的距离为30 mm；出口条件设置为压力出口，出口压力为0（表压），出口与床层的距离为60 mm；采用单求解器、SIMPLEC算法，壁面采用无滑移的标准壁面函数。模拟过程中选用空气作为流体相。

2.2.3 耦合模块设置

CFD-DEM耦合计算模型有Lagrangian模型和Eulerian模型。本工作属于气固两相流模拟，固相颗粒占用的体积大于总体积的 10%，且颗粒的体积对流体流动的影响不能忽略，因此耦合模型采用Eulerian 模型[14]。

东北四省区节水增粮行动项目依靠地下水灌溉的农田面积高达94.5%，水利部对项目建设合理开发地下水提出了明确要求。水资源论证是实施好节水增粮行动项目的重要前期工作，对科学确定发展规模，合理利用有限水资源，缓解水资源供需矛盾，提高水资源利用效率，确保节水增粮增效有重要意义。本文对项目地下水取水水源、取水影响论证思路及关键技术问题作了具体介绍。

2.3 模拟结果数据提取及分析

在Fluent后处理中，提取所需的空隙率、压力和速率数据。在固定床轴向（Z方向上）插入直线，提取径向空隙率和速率分布以及轴向压力分布，结果如图4所示。

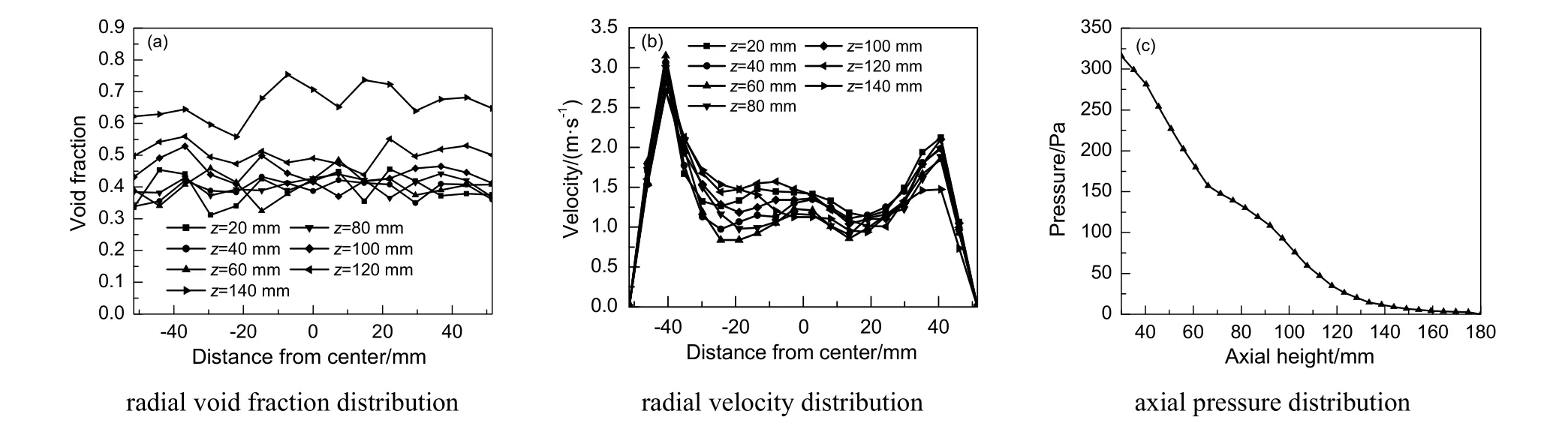
图4 空隙率、速率和压力模拟结果Fig.4 Void fraction, velocity and pressure simulation results

由图 4（a）可知，不同高度的床层空隙率不同，最高值 0.75，最低值为 0.33，但大部分在 0.38和0.53之间。由图4（b）可知，在同一截面上，速率呈波形变化，在管壁处，其值最小为0，最大值在管壁附近，为3.14 m/s。由图4（c）可知，压力值从固定床的进口到出口沿着轴向逐步减小，压降为315.90 Pa。

3 直径比对流场的影响及分析

在保持床层高度及柱状催化剂直径（10.26 mm）不变的情况下，考察不同管径和颗粒直径的比值（直径比，简写为N）对流场的影响。

3.1 催化剂床层空隙率分布

图5为截取了反应器轴向剖面（X为0的截面）的流体体积分数云图。由图可知，不同直径比下，床层内部均出现局部空隙较大的区域，这与球形颗粒以自身重力随机堆积的床层分布现象相同[15]。当N为3时，管壁附近流体空隙体积较大，壁效应显著[16]。当N为5时，有空隙局部很小的现象，但颗粒空隙分布总体较均匀，空隙率大部分集中在0.39～0.56。当N为10时，颗粒分布局部很大或很小的现象较为明显，流体进出口处流体体积分数出现波动，颗粒分布不均匀。当N为20时，流体从进口流经床层80 mm和距出口40 mm时，流体体积分数分层较为明显，变化趋势较平稳。而在床层80～110 mm，空隙率逐渐变小，颗粒堆积较密实，这使得整个床层颗粒分布均匀性相差较大。因此，N为5时，颗粒分布较为均匀。

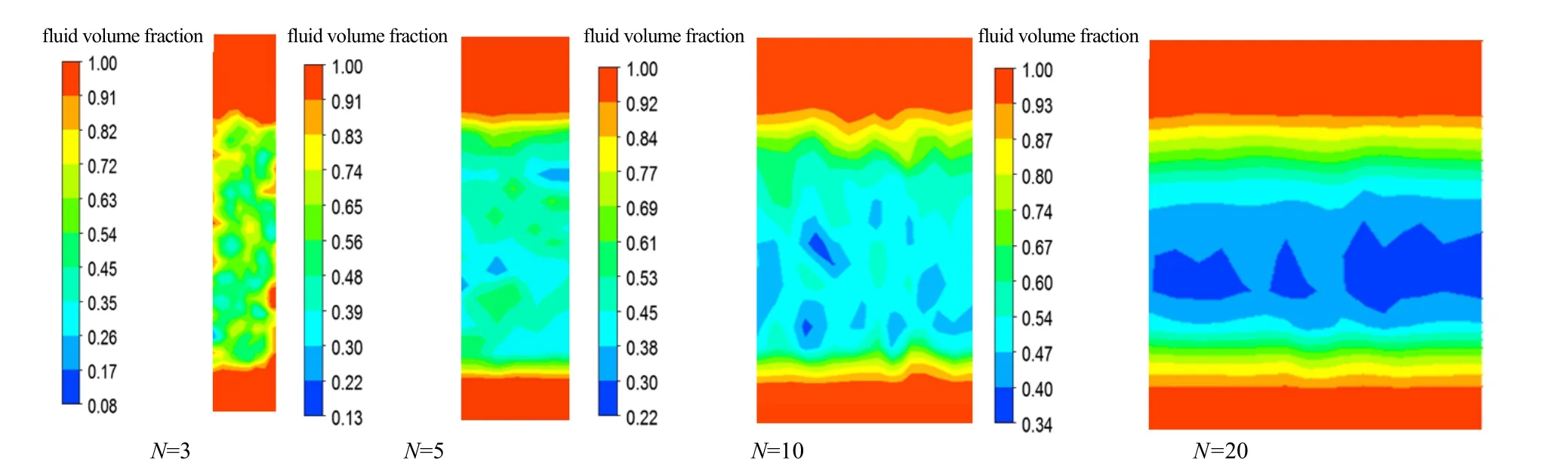
图5 X=0截面轴向颗粒空隙分布云Fig.5 Distribution contour of axial void fraction in section of X=0

图6为不同直径比下，不同床层高度（Z为20，75和130 mm）截面径向空隙率分布情况。

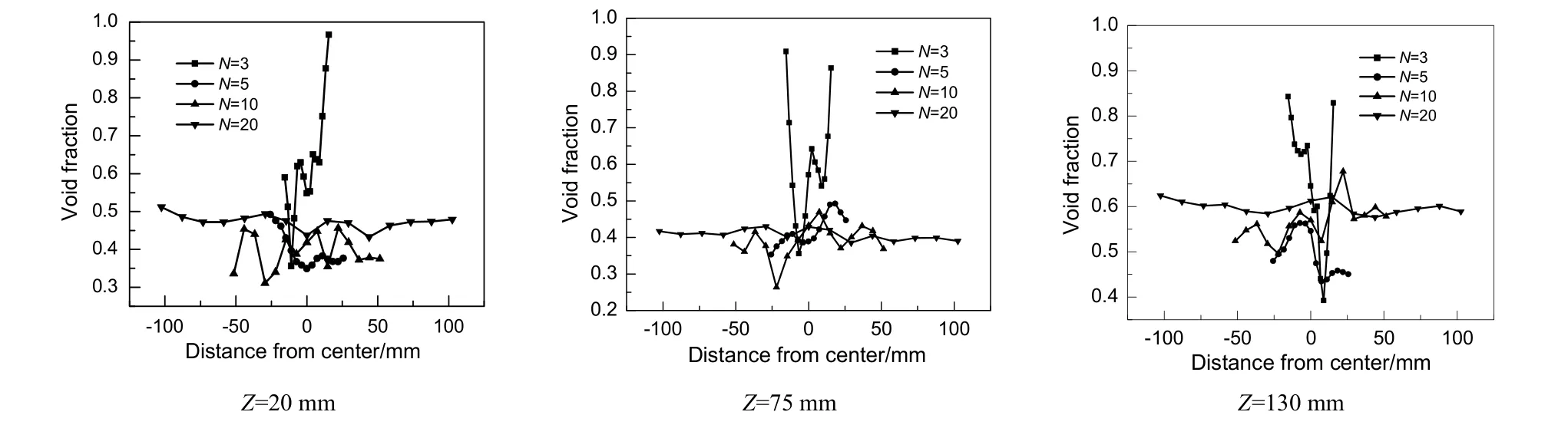
图6 不同床层高度的径向空隙率分布曲线Fig.6 Radial voidage distribution curve at different bed height

由图可知，同一高度下，不同直径比下的空隙率分布差别很大。N为3时，空隙率变化波动较大，且空隙率整体值较大；当N为5和10时，波动幅度较小；当N为20时，径向空隙率波动较为平缓，但轴向方向上空隙率分层较为明显。

3.2 床层压力分布

图7为不同直径比下固定床轴向压力变化情况。可以看出，压力从固定床的进口到出口沿着轴向方向逐渐减小，而对于不同的直径比，压降不同。当N为3，5，10和20时，进出口的压降分别为890.96，1 196.30，315.90和91.28 Pa，N为5时，压降最大，说明N为5时的床层颗粒堆积较密实[17]。

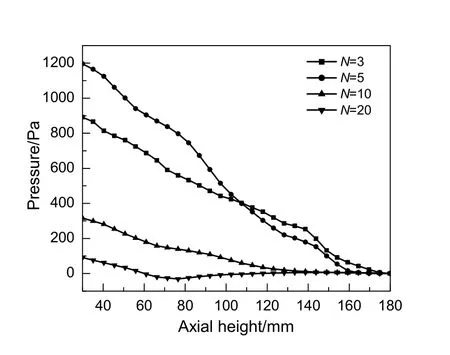
图7 固定床轴向压力分布Fig.7 Axial pressure distribution in the fixed bed

3.3 床层速率分布

图8为不同直径比下，不同床层高度（Z为20，75和130 mm）截面的速率分布云图。可以看出，在管壁区域速率都较小，壁面效应较明显。当N为3，10和20时，不同高度下的速率分布云图变化区间都较大。当N为5时，除了管壁附近，其他区域速率区间一致，表明分布较均匀。

图8 不同直径比下轴向速率分布云Fig.8 Axial velocity distribution in the fixed bed at different N

图9为不同直径比下径向速率变化规律。由图可知，当N为3，10和20时，径向最大速率均在管壁附近，分别为1.47，3.14和18.74 m/s。而N为5时的最大速率在床层中心处附近，最大值为1.63 m/s。分析图中整体速率变化趋势可看出，当N为3时，速率轴向方向上变化趋势规律不明显。当N为5时，速率变化趋势较平稳，中心附近径向波动多呈直线型。当N为10和20时，速率分布由增高到下降再升高，出现波峰，流场分布不均匀，流体流经的通道更加曲折。说明N为5的速率流场分布均匀，有利于流体传递。

图9 不同直径比下径向速率变化规律Fig.9 Radial velocity distribution in the fixed bed at different N

4 结 论

a）基于CFD-DEM耦合法，通过对模拟结果分析，得出此方法能够较好地模拟柱形催化剂床层堆积过程及流场分布特性。

b）通过分析不同直径比下X为0处轴截面的流体体积分数分布云图和空隙率径向分布曲线图，可知不同的直径比对柱形颗粒随机堆积时的影响不同，当直径比为5时，床层颗粒分布较为均匀。

c）通过分析不同直径比下床层的速度场，可知流体在直径比为5的床层下流动较平稳均匀，波动幅度较小，有利于流体传递。当直径比为3时，流体波动不大，但壁效应较为显著，不利于反应。

[1]Zhou Xiaoming, Duan Yanjun, Huai Xiulan. 3D CFD modeling of acetone hydrogenation in fixed bed reactor with spherical particles[J].Particuology, 2013, 11(6): 715-722.

[2]Freund H, Zeiser T, Huber F, et al. Numerical simulations of single phase reacting flows in randomly packed fixed-bed reactors and experimental validation[J]. Chemical Engineering Science, 2003, 58(3/6): 903-910.

[3]Guo X. Numerical simulation of flow and heat transfer in a random packed bed[J]. Particuology, 2010, 8(3): 293-299.

[4]Das S, Deen N G, Kuipers J A M. A DNS study of flow and heat transfer through slender fixed-bed reactors randomly packed with spherical particles[J]. Chemical Engineering Science, 2017, 160: 1-19.

[5]Eppinger T, Seidler K, Kraume M. DEM-CFD simulations of fixed bed reactors with small tube to particle diameter ratios[J]. Chemical Engineering Journal, 2011, 166(1): 324-331.

[6]华卫琦, 陈丰秋, 吕德伟. 催化剂颗粒的形状优化Ⅰ基本几何形状颗粒[J]. 化学反应工程与工艺, 2000, 16(2): 97-102.Hua Weiqi, Chen Fengqiu, Lv Dewei. Shape optimization of catalyst particles I: basic geometry particles[J]. Chemical Reaction Engineering and Technology, 2000, 16(2): 97-102.

[7]华卫琦, 陈丰秋, 吕德伟. 催化剂颗粒的形状优化Ⅱ有限长圆柱和常见动力学[J]. 化学反应工程与工艺, 2000, 16(2): 103-108.Hua Weiqi, Chen Fengqiu, Lv Dewei. Shape optimization of catalyst particles II. Finite length cylinder and common dynamics[J].Chemical Reaction Engineering and Technology, 2000,16(2): 103-108.

[8]Dixon A G. Correlations for wall and particle shape effects on fixed bed bulk voidage[J]. Canadian Journal of Chemical Engineering,1988, 66(5): 705-708.

[9]董宝川. 固定床反应器结构及颗粒特性对流动性能的影响[D]. 常州: 常州大学, 2015.

[10]Nemec D, Levec J. Flow through packed bed reactors, part 1: single-phase flow[J]. Chemical Engineering Science, 2005, 60(24):6947-6957.

[11]Yang J, Wang Q, Zeng M, et al. Computational study of forced convective heat transfer in structured packed beds with spherical or ellipsoidal particles[J]. Chemical Engineering Science, 2010, 65(2): 726-738.

[12]任立波. 稠密颗粒两相流的CFD-DEM耦合并行算法及数值模拟[D]. 山东大学, 2015.

[13]Hobbs A. Simulation of an aggregate dryer using coupled CFD and DEM methods[J]. International Journal of Computational Fluid Dynamics, 2009, 23(2): 199-207.

[14]王国强, 郝万军, 王继新. 离散单元法及其在EDEM上的实践[M]. 西安: 西北工业大学出版社, 2010: 97.

[15]董宝川, 刘雪东, 苏世卿. 基于CFD-DEM耦合的固定床管式反应器流体流动特性数值模拟[J]. 中国粉体技术, 2015, 21(4): 11-15.Dong Baochuan, Liu Xuedong, Su Shiqing. Numerical simulation of fluid flow characteristics of fixed bed tube reactor based on CFD-DEM coupling[J]. China Powder Science and Technology, 2015, 21(4): 11-15.

[16]Mueller G E. Angular void fraction distributions in randomly packed fixed beds of uniformly sized spheres in cylindrical containers[J].Powder Technology, 1993, 77(3): 313-319.

[17]赵庆国, 廖 晖, 李绍芬. 气体的温度和压力及颗粒形状对固定床压降的影响[J]. 化学反应工程与工艺, 2000, 16(1): 1-6.Zhao Qingguo, Liao Hui, Li Shaofen. Effect of temperature and pressure of gas and particle shape on pressure drop of fixed bed[J].Chemical Reaction Engineering and Technology, 2000, 16(1): 1-6.