寒区埋地单一腐蚀管线热-固耦合力学分析①

李巧珍 刘 扬,1b 罗 敏 迟 旭

(1.东北石油大学 a.石油工程学院；b.油气储运重点实验室；c.机械科学与工程学院；2.大庆油田有限责任公司天然气分公司)

管道运输作为继铁路、公路、水路、航空运输之后的第五大交通运输方式，在国民经济发展中起着重要作用，承担着我国70%的原油和99%的天然气运输任务。寒区油气输运管线由于所处环境的特殊性，与普通地区管线面临的风险(腐蚀、机械损伤及第三方破坏等)相比，还将承受融沉、冻胀、冰堵及露管等风险[1～3]。据不完全统计，自1995年至2015年，我国共发生各类管道安全事故一千多起，不仅造成了人员伤亡和巨大的经济损失，同时还严重地破坏了自然生态环境[4]。为了有效提高管线运行安全系数，国际和国内将完整性管理理念应用在一些油气运输管道上，取得了一定成果。

笔者基于完整性管理预防为主的基本思想，采用有限元分析方法，对寒区埋地管线可能发生的不同外腐蚀缺陷形式进行多场耦合数值模拟，分析管线力学特性随流体温度、流体压力以及腐蚀缺陷深度的变化规律，相关研究成果可为寒区输油管线完整性管理[5]中的完整性评价、风险评价及维抢修措施提供分析方法和参考依据。

1 物理模型

寒区热油管线在运行过程中，除承受重力、内压、内外温差外，还要承受随土壤特性而改变的管-土支撑力。管内原油与管壁、大气与土壤层表面属于对流传热，钢管壁、保温层和土壤层之间属于热传导。当管线发生局部腐蚀损坏后，裸露的腐蚀管线表面直接与土壤接触，从而影响土壤温度场分布，使它产生结构变形。寒区输油管线二维物理模型如图1所示。

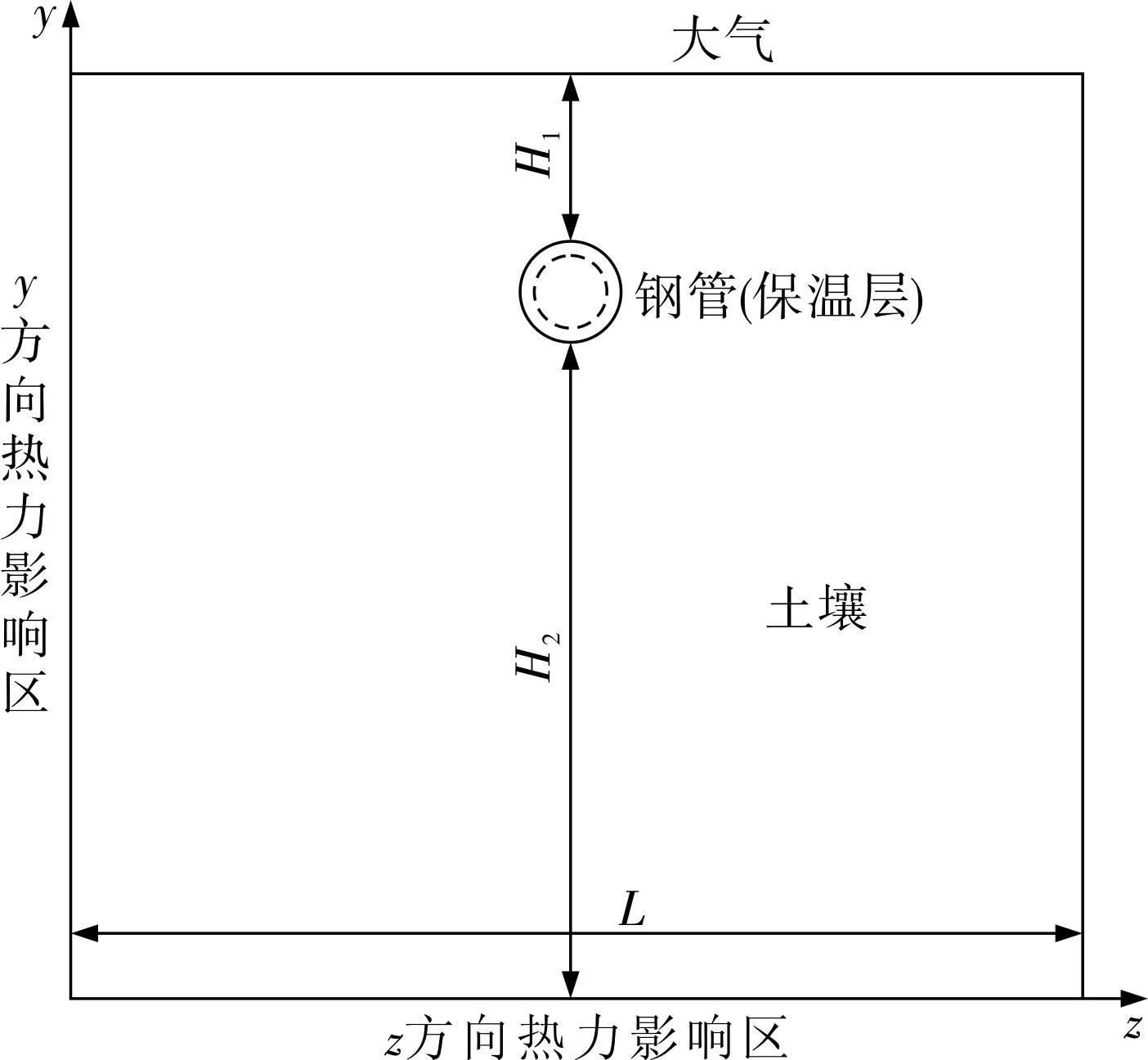
图1 寒区输油管线二维物理模型

2 热-固耦合数学理论

2.1 温度场方程

寒区输油管线在运行过程中，管道周围土壤温度场会随季节推移而变化，管线与周围土壤会发生热交换，其温度场热量平衡控制微分方程为：

(1)

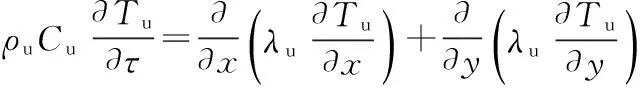
(2)

管线钢非稳态导热微分方程：

(3)

保温层非稳态导热微分方程：

(4)

其中，λf、λu、λ1、λ2分别为冻结区土壤、融化区土壤、管壁、保温层导热系数；ρf、ρu、ρ1、ρ2分别为冻结区土壤、融化区土壤、管壁、保温层密度；Cf、Cu、C1、C2分别为冻结区土壤、融化区土壤、管壁、保温层热容；Tf、Tu、T1、T2分别为冻结区土壤、融化区土壤、管壁、保温层温度；τ为时间。

2.2 热-固耦合方程

平面问题中的平衡微分方程为：

(5)

对于热-固耦合问题，由于温度变化会产生附加的热应力和热应变。因此，假设埋地管线的初始温度为Tg0，当温度升高至温度Tg(该温度与温度场控制方程相关)时，管线发生膨胀产生热应变，热应变计算公式为(β为管线的线膨胀系数)：

εhot=-β(Tg-Tg0)

(6)

因此，得到管线的物理方程为：

(7)

计算整理得到：

(8)

几何方程在平面问题中的简化形式为：

(9)

将式(8)代入式(5)中，并利用几何方程式(9)，得到管线耦合变形方程：

(10)

其中，u和v为腐蚀管线在内压、温差、土壤力共同作用下产生的位移分量；fx和fy为腐蚀管线所受力的分量。

上述方程中包含体现温度场变化的耦合项，需要联立温度场方程才能进行求解。

2.3 定解条件

对于耦合的导热方程和应力场方程，给出相应的初始条件和边界条件。

2.3.1导热问题数学模型的定解条件

导热问题数学模型的定解条件分为初始条件、边界条件和连续条件。假设研究的矩形空间区域为Ω，域边界为Γ。

2.3.1.1初始条件

大气温度随季节变化而变化，其表达式为：

Ta|τ=0=φ(τ)

(11)

土壤初始温度：

Tu|τ=0,Ω=T0

(12)

2.3.1.2边界条件

土壤深度H处的恒温层边界条件：

T|y=H=T0′

(13)

矩形区域水平方向的边界条件：

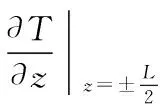
(14)

土壤表面和大气的对流边界条件：

(15)

原油和管道内壁的对流边界条件：

(16)

2.3.1.3连续条件

在移动的冻胀、融沉交界面Γ(t)上，连续条件和守恒条件为：

Tf(Γ(τ),τ)=Tu(Γ(τ),τ)=Tm

(17)

(18)

保温层外壁和土壤连接面处的温度关系式为：

T2|r=(R+δ0+δt)-=T|r=(R+δ0+δb)+

(19)

保温层外壁和土壤连接面处的导热量关系式为：

(20)

管道外壁与保温层内壁连接面处的温度关系式为：

T1|r=(R+δ0)-=T2|r=(R+δ0)+

(21)

管道外壁与保温层内壁连接面处的导热量关系式为：

(22)

其中,T为土壤温度；Tw为地面温度；Ta为大气温度；T0′为土壤恒温层温度；λs为土壤导热系数；h、h1分别为地表土壤与大气间的换热系数、原油与管道间的换热系数；L、H分别为管道热力影响区域在z、y方向上的边界坐标；Tm为土壤的冻结温度；X为水的相变潜热；n为移动边界的方向矢量；R为管线半径；δ0为钢管壁厚；δb为保温层厚度。

2.3.2管线数学模型的定解条件

位移边界条件为：

(23)

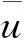
应力边界条件：

(24)

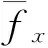
3 有限元分析

3.1 基础数据

图2 全年地表温度变化曲线

图3 L360管线钢的真实应力-应变关系曲线

管线钢其他基础参数见表1[7]，保温层及土壤相关数据参见文献[8，9]数据。

表1 管线钢基础参数

3.2 边界条件

管线内部承受4MPa压力；地表施加全年地表最低温度并考虑对流换热效应；土壤恒温值为4℃(地下10m[10])；管线内部承受流体温度为48℃。

管、保温层、土壤可简化成10m×10m的特殊矩形区域[11]。依据结构对称性，建立1/2模型，管线处的剖面施加对称位移约束，水平另一侧忽略横向位移；地下10m忽略纵向位移；接触大气一侧土壤自由。

3.3 有限元模型

采用含中间节点的二维8节点耦合场单元PLANE223分别对管线本体、保温层及土壤进行结构离散，离散过程中对管线、保温层及邻近保温

层土壤区域网格细化，远离管线区域土壤网格相对稀疏。土壤采用Drucker-Prager弹塑性本构模型。整体结构有限元模型如图4所示，管线腐蚀部位见局部放大图。

3.4 计算结果分析与讨论

通过热-固耦合分析，得到寒区腐蚀管线全年应力、应变变化规律分别如图5、6所示，腐蚀管线年应力最大值和年应变最大值分布位置如图7、8所示。

图4 有限元模型

图5 腐蚀管线应力年变化曲线

图6 腐蚀管线应变年变化曲线

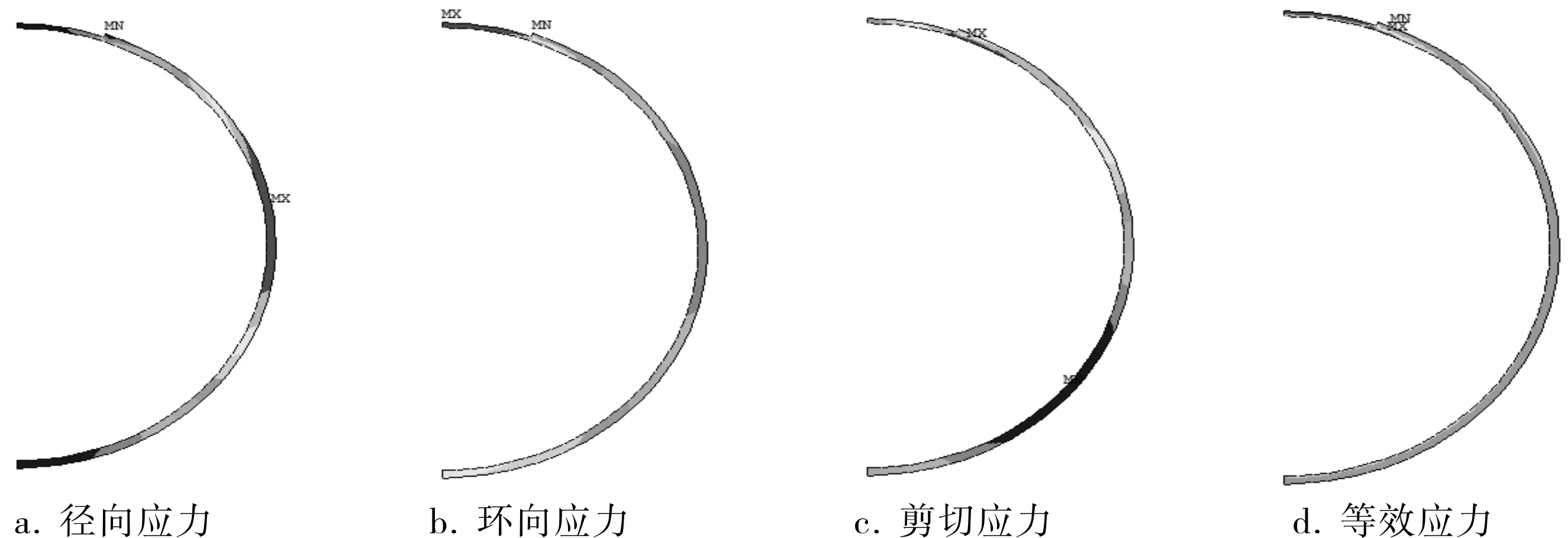
图7 腐蚀管线年应力最大值分布位置

图8 腐蚀管线年应变最大值分布位置

结合图5和图7可以看出，径向应力最大值出现在腐蚀管线中部位置，为130.0MPa，出现季节为11月，即全年大气环境温度由零上温度转至冰点以下温度的季节；环向应力最大值出现在管线的腐蚀坑处，为224.0MPa，出现季节为1月，即全年大气环境温度最低的季节，而且环向应力分布规律符合薄壁承受内压腐蚀圆筒的应力分布规律；剪切应力最大值出现在腐蚀坑与完好管壁交界处附近，为81.1MPa，出现季节为7月，即全年大气环境温度最高的季节；等效应力最大值出现在管线的腐蚀坑处，为251.0MPa，出现季节为1月，即全年大气环境温度最低的季节。由此可见，受内压作用的埋地腐蚀热油管线，在承受内压、温度及土壤支撑作用下，依旧为环向应力起主导作用。

结合图6和图8可以看出，径向应变全年变化幅度较小，最大值出现在腐蚀管线中部位置，值约为0.000 6；环向应变全年变化幅度较径向应变变化幅度稍大些，最大值出现在管线腐蚀坑处，值为0.001 0，出现季节为11月与次年3月之间，即全年大气环境温度最低的季节，这是由于腐蚀区域管壁变薄，在与其他壁厚无损坏的管壁位置承受相同内压时，表现出性能急剧下降的特性；米塞斯应变最大值出现在腐蚀坑边缘处，最大值为0.001 2，出现季节为11月与次年3月之间。由此可见，受内压埋地腐蚀热油管线变形以环向变形为主。

将多场耦合分析获取的数值解分别与采用Modified ASME B31.G法[12]、RPA法[13]和DNV-RP-F101法[14]计算得到的腐蚀管线失效压力理论解进行误差对比，结果见表2。

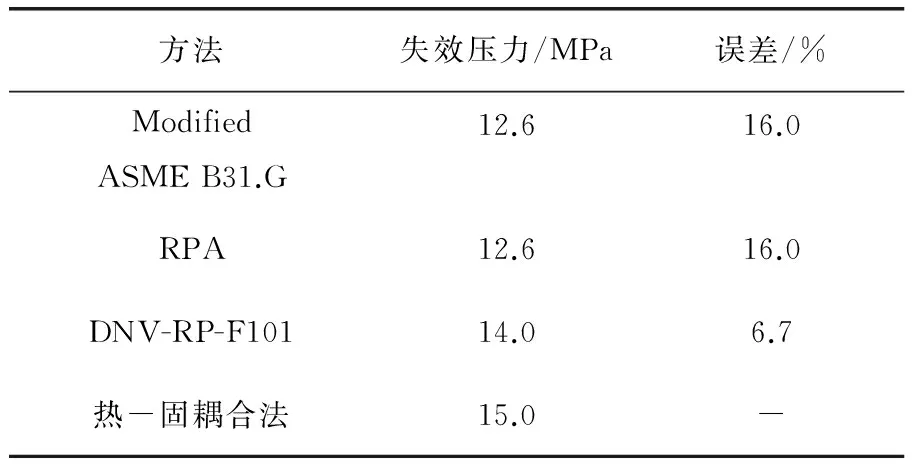
表2 单一腐蚀管线失效压力数值解

由表2可以看出，采用Modified ASME B31.G法与RPA法计算得到的失效压力理论值相对保守，采用DNV-RP-F101法计算得到的失效压力理论值与热-固耦合有限元方法获取的数值解较为接近，误差为6.7%。该表格数据可以在一定程度上证明本文热-固耦合方法、模型简化以及边界条件处理的正确性。

基于应变的失效判据[15]要求本工况下腐蚀管线全年安全运行时其应变小于0.005 3，因此，该管线全年均可安全运行。

4 影响因素分析

4.1 流体温度对腐蚀管线力学特性影响规律研究

设定工况：相对腐蚀深度为0.4、管线承受4MPa内压时，分别探讨流体温度为40、48、53、60、80℃的管线力学特性变化规律。通过对流经不同温度流体的腐蚀管线进行热-固耦合分析，整理其应力场和位移场结果数据，得到腐蚀管线应力和应变随流体温度变化的曲线分别如图9、10所示，腐蚀管线应变最大值分布位置如图11所示。

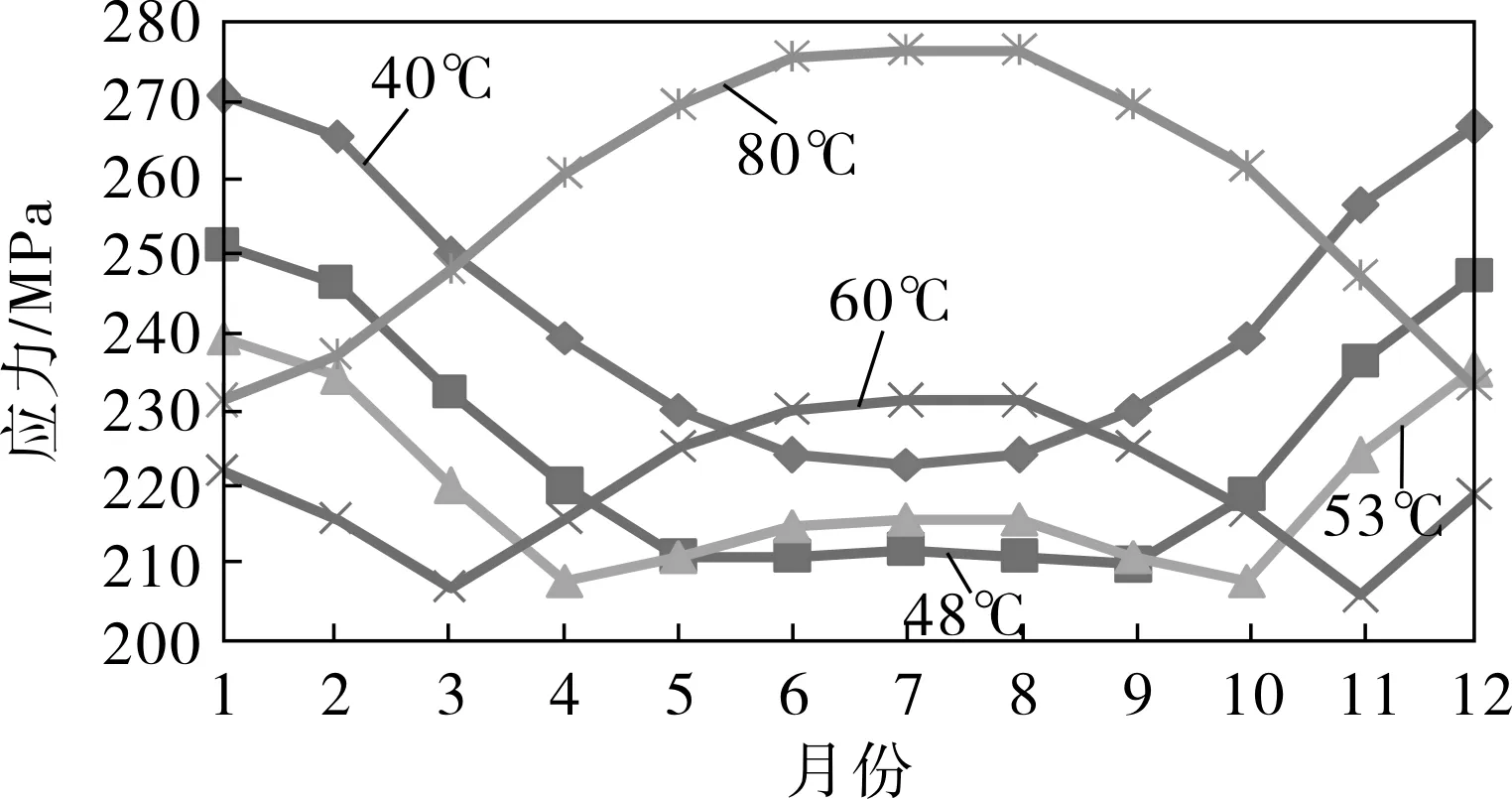
图9 腐蚀管线应力随流体温度变化曲线

图10 腐蚀管线应变随流体温度变化曲线

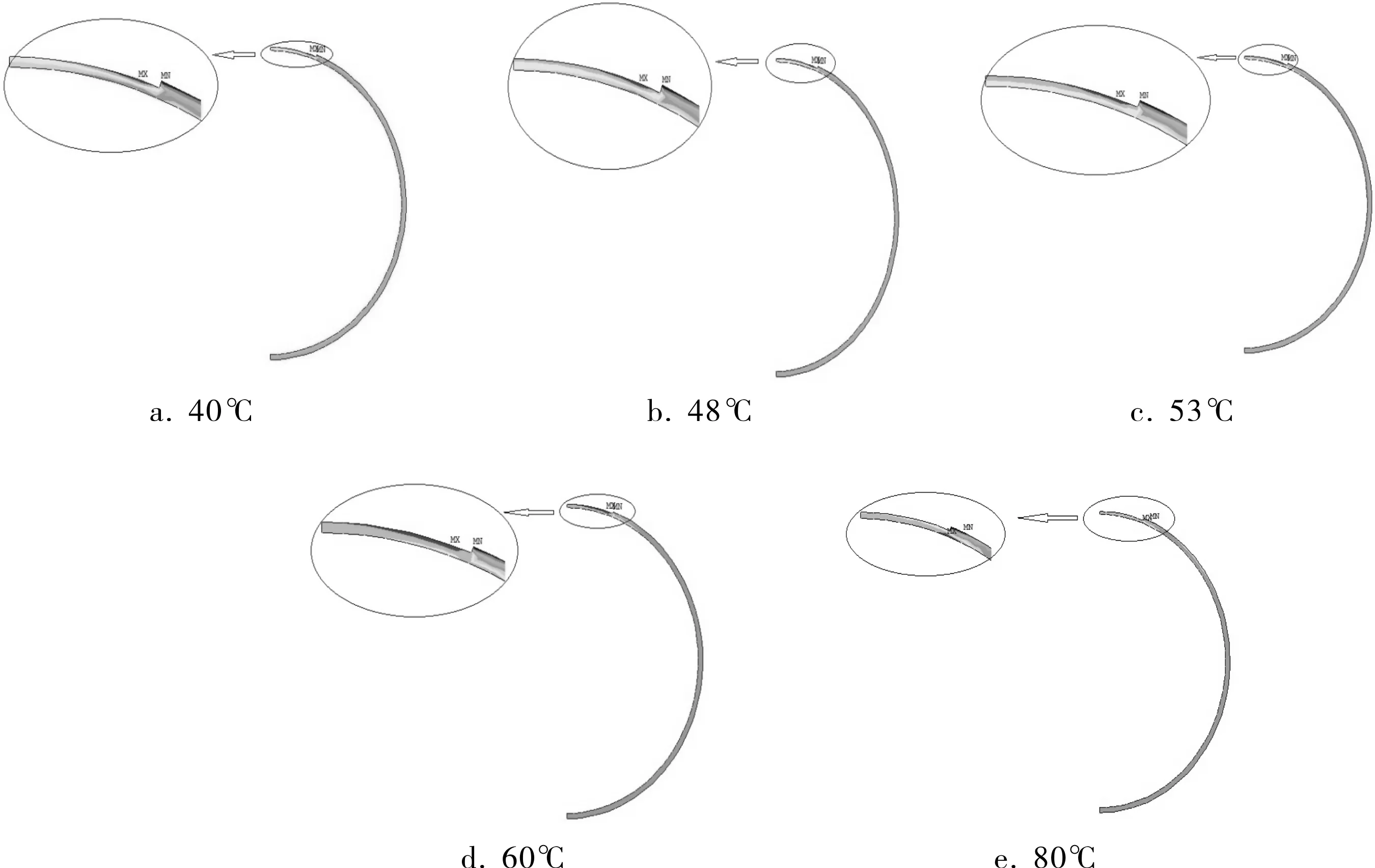
图11 不同流体温度下腐蚀管线应变最大值分布位置

由图9可以看出，管线应力随流体温度变化呈现季节性差异。其中11月到次年3月(即大气环境温度为冰点以下温度的季节)管线等效应力均随流体温度的升高而降低；4～10月(即大气环境温度为冰点以上温度的季节)随着流体温度的升高呈现先降低后升高趋势，且流体温度越高，这种先降低后升高的趋势就会越明显。

结合图10、11可以看出，腐蚀管线应变随流体温度年变化规律与应力年变化规律一致，最大值出现在腐蚀坑处。当流体温度高于48℃时，随着温度升高，腐蚀管线夏季输油时面临的风险呈升高趋势，当温度达到60℃时，腐蚀管线夏季输运风险(6～8月)会高于冬季输运。当管内流体温度增加1倍，管线应变最大变化幅度为23.9%。这是由于土壤在冬冷季节发生冻胀，而腐蚀后的管线缓解并降低了冻胀程度所致。

4.2 流体压力对腐蚀管线力学特性影响规律研究

设定工况：相对腐蚀深度为0.4、管内流体温度为48℃时，分别探讨流体压力为3.0、3.5、4.0、4.5、5.0、6.0MPa的管线力学特性变化规律。通过对流经不同压力流体的腐蚀管线进行热-固耦合分析，整理其应力场和位移场结果数据，得到腐蚀管线应力和应变随流体压力变化曲线分别如图12、13所示，腐蚀管线应变最大值分布位置如图14所示。

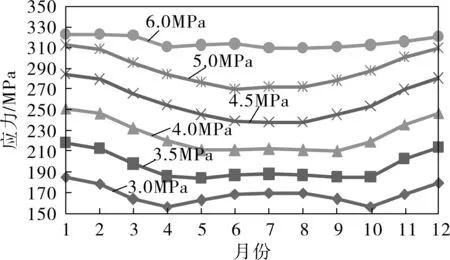
图12 腐蚀管线应力随流体压力变化曲线

图13 腐蚀管线应变随流体压力变化曲线

图14 不同流体压力下腐蚀管线应变

由图12可以看出，当大气环境温度一定时，随着流体压力的增加，腐蚀管线应力呈明显增加的趋势；当流体压力一定时，腐蚀管线全年应力呈现季节性差异。管线应力年变化曲线由3.0MPa时的减、增、减、增双峰曲线模式，逐渐过渡成减、增的单峰曲线模式，当流体压力达到6.0MPa时，管线的全年应力均较高，其中最高值能达到322.0MPa。

结合图13、14可以看出，随着流体压力增加，腐蚀管线应变呈总体增加趋势。当流体压力低于6.0MPa时，腐蚀管线全年应变呈现季节性差异；当流体压力高于6.0MPa时，管线全年应变均较高。当管内流体压力增加1倍时，管线应变增加74.3%。因此，对于含腐蚀缺陷的高压管线，其全年运行过程均应引起足够重视，以有效避免管线事故的发生。

4.3 相对腐蚀深度对腐蚀管线力学特性影响规律研究

设定工况：管线承受4MPa内压、流体温度为48℃时，分别探讨相对腐蚀深度为0.3、0.4、0.5、0.6的管线力学特性变化规律。通过对含不同相对腐蚀深度的腐蚀管线进行热-固耦合分析，整理其应力场和位移场结果数据，得到腐蚀管线应力及应变随相对腐蚀深度变化曲线分别如图15、16所示，腐蚀管线应变最大值分布位置如图17所示。

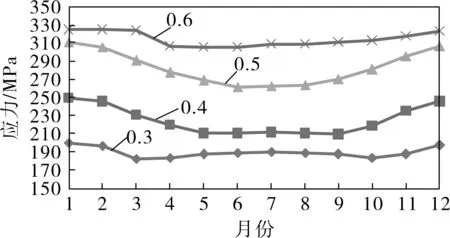
图15 腐蚀管线应力随相对腐蚀深度变化曲线

图16 腐蚀管线应变随相对腐蚀深度变化曲线

由图15可以看出，随着相对腐蚀深度增加，管线应力呈明显增加趋势；当相对腐蚀深度由0.3增至0.6时，应力增幅为61.7%。

结合图16、17可以看出，腐蚀管线应变随相对腐蚀深度年变化规律与应力年变化规律相似，均随相对腐蚀深度的增加而增大。当相对腐蚀深度增加一倍时，最大应变增幅能达到61.7%，最大值始终位于管线腐蚀坑中。因此，在载荷边界条件和位移边界条件均相同的情况下，管线含有的腐蚀缺陷相对腐蚀深度越深，其运行时的安全性需在全年均引起注意和重视。

图17 不同相对腐蚀深度的腐蚀管线应变最大值分布位置

5 结论

5.1将多场耦合数值解分别与腐蚀管线失效压力理论解进行误差对比，最小误差为6.7%，一定程度上证明了本文热-固耦合方法、模型简化以及边界条件处理的正确性。

5.2在单一腐蚀管线热-固耦合影响因素分析中，分别探讨了流体温度、流体压力以及相对腐蚀深度对管线应力场及位移场的影响规律。结果表明：三类影响因素对管线力学特性影响呈现季节性差异，且影响程度由强到弱依次为流体压力、相对腐蚀深度、流体温度。其中，流体压力增加1倍，管线应变增加74.3%；相对腐蚀深度增加1倍，管线应变增加61.7%；流体温度增加1倍，管线应变最大变化幅度为23.9%。

[1] 房剑萍,段庆全.低温冻土区油气管道失效事故分析[J].油气储运,2016,34(3):7～10.

[2] Clark J, Phillips R.Centrifuge Modeling of Forst Heave of Arctic Gas Pipelines[C]. Proceedings of the 8th International Permafrost Conference. Zurich：2003：151～156.

[3] Palmer A C, Williams P J. Frost Heave and Pipeline Upheaval Buckling [J]. Canadian Geotechnical Journal, 2003, 40(1): 1033～1038.

[4] 房剑萍.国内外油气管道事故案例分析[J].石油和化工设备,2016,19(9):90～93.

[5] 吴志平,蒋宏业,李又绿,等.油气管道完整性管理效能评价技术研究[J].天然气工业,2013,33(12)：131～137.

[6] 赵潇,马延霞,吴志峰,等.X52长输管线在悬空状态下的安全研究[J].机械科学与技术,2015,34(10):1589～1593.

[7] GB 150-2011，压力容器[S]. 北京：中国标准出版社，2011.

[8] 李南生,谢利辉,陈薛浩.寒区浅埋输油管线冻胀安全性分析[J].结构工程师,2008,24(1):35～40.

[9] 李慧.地震载荷作用下多年冻土区斜坡路堤稳定性分析[D].北京:北京交通大学，2010.

[10] 陈从磊,黄启玉,王乾坤.正反输送管道停输再启动数值模拟分析[J].石油化工高等学校学报,2015,28(2):77～82.

[11] 吴国忠.埋地输油管道停启传热问题研究[D].大庆:大庆石油学院,2007.

[12] ASME B31.G，Manual for Determining the Remaining Strength of Corroded Pipelines[S]. USA：The American Society of Mechanical Engineers，2009.

[13] Andrade E Q, Benjamin A C. Structural Evaluation of Corrosion Defects in Pipelines: Comparison of FE Analysis and Assessment Methods[C].Proceedings of the Fourteenth (2004) International Offshore and Polar Engineering Conference, Toulon：2004：23～28.

[14]DNV-RP-F101，Recommended Practice:Corroded Pipelines[S].Oslo: Det Norske Veritas，2004.

[15] 帅健.管线力学[M].北京:科学出版社,2010:163～166.