基于普通Kriging法的速度场模型建立

张 勇, 梁冠军, 黄展华

(滁州职业技术学院 土木工程系,安徽 滁州 239000)

自2008年7月1日开始，我国正式采用2000国家大地坐标系，且此后的各类测绘地理信息成果一律采用2000国家大地坐标系.而我们国家的CGCS2000框架目前只能提供相应于ITRF97框架、2000历元的静态坐标.因此不利于科研和工程中应用最为普及的GPS精确定位(ITRF2005框架和当前历元)，有进行转换的必要性.故须以国家能获得的高分辨率速度场资料建立我国地壳运动速度场模型，并在此基础上进行框架转换及历元归算，方可将测量成果纳入我国2000大地坐标系.

基于上述原因，通过插值或数值模拟方法求得具有足够点位密度且分布均匀的速度场已经成为迫切需要解决的问题.国内外不少专家学者已经采用多种方法建立了我国大陆区域地壳运动速度场.刘经南等采用多面函数法对中国区域水平运动进行了数字模拟[1]，杨少敏等用双三次样条函数建立了中国大陆构造形变场[2]，蒋志浩采用有限元插值方法(三角形三次多项式插值算法)建立了中国地壳运动速度场模型[3].从数学的角度发现插值点与已知点的关系是这些模型的优点，但是没有充分考虑板块固有的物理及力学意义，因此是有缺陷的.

20世纪中叶地质学家D.G.Krig首先提出了Kriging插值方法，该方法用变异函数为工具，是一种线形无偏且计算准确的空间内插方法，得到了越来越广泛的应用.大量实践证明，该插值法建立起来的模型能够很好地反映空间变化特性，当变量之间存在着一定空间关联特性时效果更优.Kriging方法在矿产储量、降雨量、气温数据等学科领域的应用及研究均取得了很好的结果，常文渊通过对梯度距离平方反比法(GIDW)、样条函数法(Spline)等几种插值方法的比较，发现Kriging法精度最高，实现的关键在于充分考虑空间场性质及正确选择参数[4].潘永地等用Kriging法分析降雨量的空间关联性，得出Kriging法是一个比较成熟且精确度高的插值方法[5].从现有的文献来看，迄今为止尚没有将该方法用于速度场模型建立.本文采用美国GPS站点的观测数据，对用普通Kriging法进行速度场数据插值的可行性进行探讨.

1 克里格法的理论基础

假设x(b,l,v)是插值区域内的一点，其中b是该点的经度值，l是该点的纬度值，v是速度值且满足本征假设或二阶平稳假设.x1,x2,…,xn分别为插值有效范围内的n个已知点，那么对待插值点，可以通过n个有效样本值v(xi)的线性组合来表示其估计值v*(x)，即

(1)

式中：λi为反映重要程度的比例系数，它决定了已知样本v(xi)在建立模型后对插值影响的大小，因此想要最优的估计v*(x)，怎样计算和选择权重系数λi尤为重要.

求取比例系数时需要满足以下两个条件，一是使v*(x)估计值偏差的数学期望为零；二是使估计值v*(x)和实际值v(x)之差的平方和最小[6].两个条件可用下列公式表示：

Ε[v*(x)-v(x)]=0

(2)

σv2=Var[v*(x)-v(x)]=Ε[v*(x)-v(x)]2->min

(3)

假设v(x)的数学期望为m；根据无偏条件可得：

(4)

前文已经假设满足二阶平稳条件，因此推导估计方差的计算公式为：

(5)

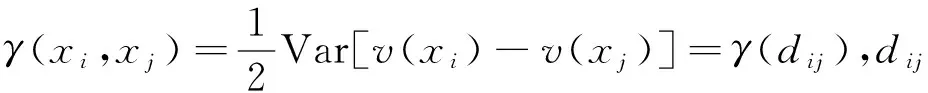
求估计方差式(5)最小值且满足式(4)的约束条件，为条件极值问题，采用拉格朗日算法：

(6)

式中u为引入的一个新的参数(拉格朗日乘子)，进行求偏导即可得普通kriging方程组：

(7)

方程组中的未知数和方程数数目相等，均为n+1，因此能解方程求出λi，最后代回式(1)可求出估值v*(x).

2 基于普通Kriging法的速度场数据插值法

采用前文提出的普通Kriging方法，以美国西部GPS测站数据为例，建立基于普通Kriging法的美国西部速度场模型，详细步骤如下：

1)从sopac网上获取美国西部的速度场数据xi(b,l,vb,vl)，i=1,2,…,n，获得了915个已知点数据，其中900个点作为已知点参与插值模型建立，剩余的15个点假设为未知点，通过与模型插值结果比较来验证插值精度.

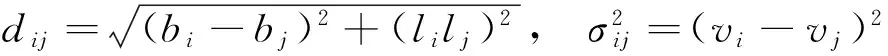
3)按距离分组后求距离的均值及对应的半变异函数值：

5)求偏导得到方程组式(7)，求解后代入式(1)，对未知点速度场数据进行插值估计.

3 Kriging插值效果检验

3.1 半变异函数拟合

通过反复验证，结合前文提出的距离组选取方法，最终将900个测站数据划分为12个距离组，并求出了半变异函数值(与距离组一一对应).表1列出了纬度方向上各个距离组的距离值和相应的半变异函数值以及落在该距离组的数据个数.

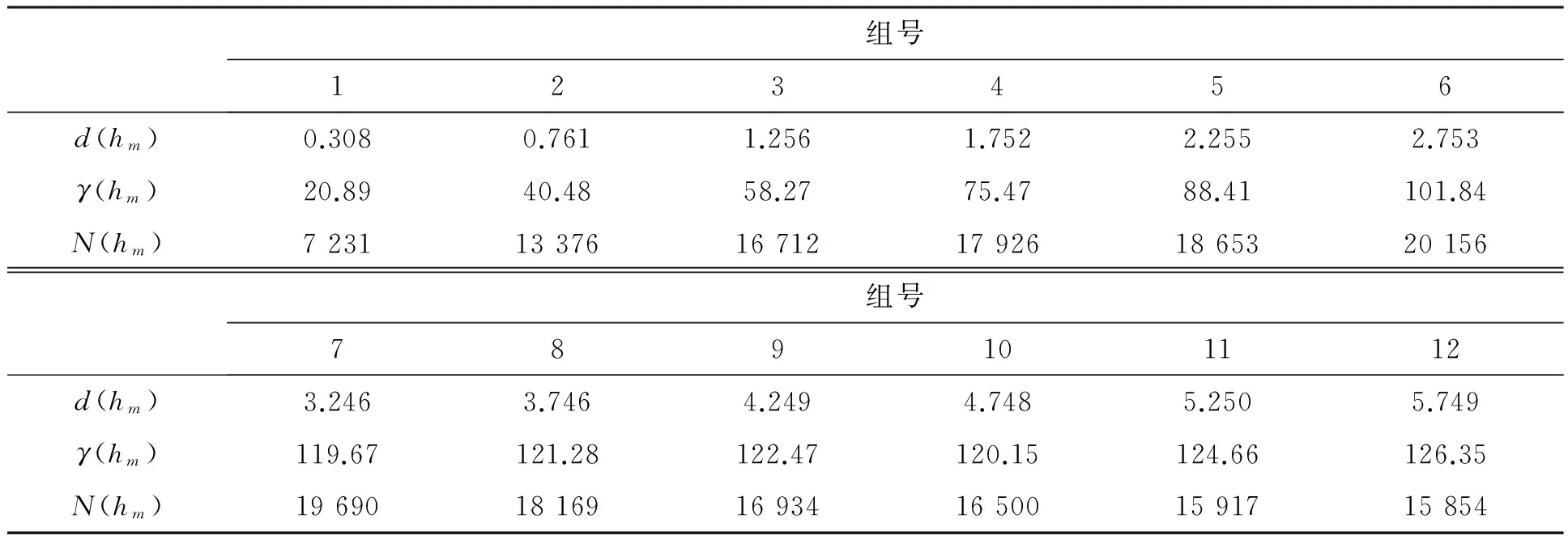
表1 纬度方向距离值、半变异函数值和落入每个距离组的个数

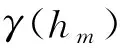
γb(h)=2.62+51.73h-10.37h2+0.69h3

γl(h)=4.68+50.92h-5.78h2+0.09h3

3.2 Kriging插值精度分析

本文采用15个点作为验证点来检验插值效果，插值过程中为防止数据丛聚带来的数据代表性不强，采用了八分搜寻，保证各象限均有代表数据.根据15个点的估计值与真值差分析，B方向的误差均值为-0.22 mm，中误差为1.71 mm；L方向的误差均值为0.02 mm，中误差为2.09 mm.B方向和L方向最大误差均不超过4 mm.

为了比较Kriging法的优劣，本文还实现了多面函数拟合法和反距离加权法[7]的速度场模型建立，选用的原始数据和验证点数据与Kriging法完全相同，同样得到验证点的估计值与真值差值，反距离加权法插值中B方向的中误差为2.06 mm，L方向的中误差为2.07 mm，多面函数拟合法B方向的中误差为2.07 mm，L方向的中误差为1.7 mm.由此可见，在本文算例中，Kriging法速度场模型符合精度最高，因为本文Kriging法推导过程中假设插值的速度场满足平稳随机场条件，但如果不满足的话则插值效果并不理想.此外强调，虽然本文算例的计算结果显示Kriging法建立的速度场模型精度比另外两种方法更高，但这并不代表在任何情况下都是如此.

4 结语

Kriging方法是地质统计学的重要组成部分，在地质找矿及土壤生态研究等领域中，基于区域化变量理论的Kriging空间插值方法已经得到广泛应用.本文将其引入速度场模型建立中，通过对验证点的精度分析表明Kriging方法对较大尺度的速度场数据插值是可行的，且插值结果十分理想，优于多面函数拟合法和反距离加权法，插值精度达到了毫米级.

[1] 刘经南,施闯,姚宜斌，等.多面函数拟合法及其在建立中国地壳平面运动速度场模型中的应用研究[J].武汉大学学报(信息科学版),2001,26(12)：500-508.

[2] 杨少敏,游新兆,杜瑞林,等.用双三次样条函数和GPS资料反演现今中国大陆构造形变场[J].大地测量与地球动力学,2002,22(1)：16-30.

[3] 蒋志浩,张鹏.基于CGCS2000的中国地壳水平运动速度场模型研究[J].测绘学报,2009,38(6)：471-476.

[4] 常文渊,戴新刚.地质统计学在气象要素场插值的实例研究[J].地球物理学报,2004,47(6)：982-990.

[5] 潘永地,徐为根.沿海丘陵地区面雨量估算插值方法试验比较[J].气象科学,2005,25(2)：124-132.

[6] 刘承香.基于Kriging插值的数字地图生成算法研究[J].深圳大学学报(理工版),2004,21(4)：295-300.

[7] 刘文岭,李伟.空间插值法对渤海天津海域海水盐度分布的影响[J].盐业与化工,2009,39(2)：43-46.