基于块融合机制的WSN数据误差追踪算法
2018-01-29张昊
张 昊
(安徽城市管理职业学院 信息工程系,合肥 230011)
随着工业化4.0的不断推进及相应电子加工技术的不断进步,WSN网络性能也不断的得到了强化,在国民经济中发挥了重要的作用.WSN网络能够在各种极端区域内,如深海海底、严重核辐射沾染地带等智能化的获取数据[1].除了这些常用领域之外,各种民生系统如智能监控体系平台、大健康分析系统、交通智能调度系统中也广泛的使用采取WSN网络,极大的促进了社会生产力水平的进步[2].如GAO C等[3]提出了一种基于云拥塞调度控制机制的误差追踪算法,能够有效的应对出现拥塞时的传感误差,可以在数据密集传输时保障传感数据的误差水平基本保持均衡状态;然而由于该算法的拥塞调度机制对节点能量不足的情况考虑不足,当节点因能量水平下降而出现信号衰减时,整个网络的传感误差水平将出现显著的上升.CHEN D等[4]提出了一种基于层次矢量一体化投射机制的WSN误差追踪算法,采取区域映射机制,将误差矢量投影到信号强度较好的区域内进行矢量传输,有效的降低了传感误差水平;然而该算法需要对误差矢量进行层次映射,因而对网络环境的稳定性要求较高,当网络环境处于波动时,网络的传感误差水平也会随之出现严重的波动.ZHOU C等[5]基于二维码校验算法,通过将全部节点进行二维码映射,能够实现在高密度节点环境下的数据交流矩阵构建,实现数据误差矢量的正交化减缓,然而该算法对中央控制中心的实时性要求很高,容易因中央控制节点拥塞而出现严重的数据瘫痪现象.
鉴于当前研究中存在的不足,本文提出了一种基于块融合与能量排序机制的WSN网数据误差追踪算法;采取矢量化追踪机制,构建误差追踪阈值实现数据传感期间的有效消波降噪;随后针对消波降噪后的数据记录构建二次误差削减流程,采取块融合的方式对传输误差进行二次削减.最后采用MATLAB仿真实验环境证明了本文算法的优越性.
1 本文WSN数据误差追踪算法
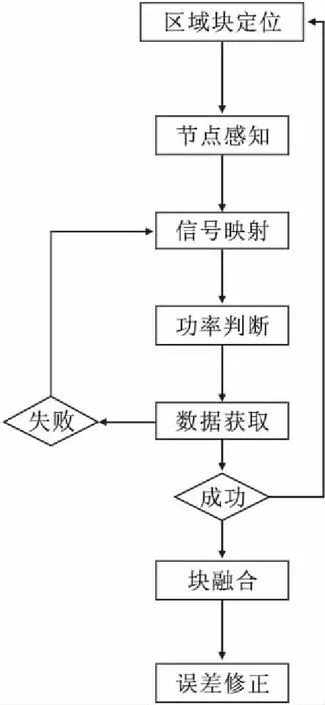
图1 本文算法流程图
本文算法主要由矢量化追踪、块融合误差削减两步流程构成(见图1).首先需要根据不同节点隶属的区域块,采用信号映射的方式对区域块内的节点进行信号映射,有效的获取信号的传感性能并根据节点信号功率进行位置定位;随后采用块融合的方式对传输波动进行降噪,从而实现了数据误差的有效追踪.
1.1 基于块区域的矢量化追踪机制
考虑到WSN网络均采用一定的方式进行分区,且不同块区域之间的信号强度与节点呈现一定的比例分配关系[6],因此,可采取块区域阈值的方式实现对不同区域内节点信号的追踪.不妨设i为第i个块区域内的中央控制节点,其拓扑位置为γi,且该块区域与相邻的块区域中存在数据传输的块区域中央控制节点的拓扑位置为γij,则根据块区域的数据分布特性可得[7]:
γi=μ′(B)γij+RBPrev
(1)
相应的误差γi′满足如下的数学表达式:
γi′=μ(B)γi+BPrev
(2)
式(1)和(2)能够准确的获取某个块区域中央控制节点与其余块区域内的中央控制节点间的拓扑位置关系,然而单纯采取上述方式也存在显而易见的弊端:需要定时测量不同块区域内部的节点拓扑信号质量,且随着传输周期的不断扩大,节点的传输性能也将不断的降低,因此需要对模型(1)~(2)进行改进,以便能够适应节点性能不断下降的实际情况.

图2 基于块区域的矢量化追踪机制
对此,本文采取矢量化追踪机制(见图2),将获取的块区域节点进行矢量重心获取,以便降低追踪过程中的误差.
首先,根据模型(1)获取传输带宽μ(B)最佳的块区域,进行矢量重心获取,该矢量重心拓扑位置γ获取方式如下:
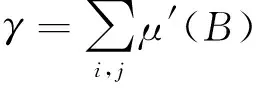
(3)
在传感网络运行期间,其节点的收发功率将收敛于0[8],故模型(3)可演变为:
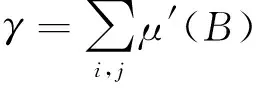
(4)
式(4)中,γ为B的概率矢量映射.
且γ与γi同时满足如下条件:
γi⟹γ
(5)
因此,γi可转换成:
γi=μ′(B)γij
(6)
依据式(6),可将γi的误差γi′写为:
γi′=μ(B)γij
(7)
模型(7)中的参数情况同模型(1)~(6).
矢量追踪步骤如下:
Step 1:由式(3),获取到块区域的中央控制节点及相应的拓扑位置;
Step 2:由式(4),获取信号强度映射最佳的中央控制节点,并取得相应的拓扑位置;
Step 3:由式(5)~(7),求得精确拓扑位置,转Step 4;
Step 4:由式(7),求得坐标的误差修正,流程结束.
1.2 基于块融合的误差削减
考虑到进行误差追踪时,块区域内部的中央控制节点与周围存在数据交换的块区域之间的拓扑距离为重要的追踪参数;且对于任意一个中央控制节点而言,其与周围块区域间数据传输密切程度越高,则追踪过程中的数据准确程度也就越高[9].由于对于确定的中央控制节点而言,在进行数据交换过程中若与某一块区域间的连通程度越大,则说明该节点的追踪误差也就越小,便于数据交换过程中的信息追踪[10].
设i为某个中央控制节点,其与之进行数据交换的节点个数为λi,则λi满足如下的关系:
(8)
其中v为与i相邻的节点j的集合,与i相邻的节点数量越多,则λi的权值越大.
不妨设i的连通指数为ηij,则ηij满足如下的关系:
(9)
相关参数同模型(1)和模型(2).
式(9)中获取的连通指数能够有效的反映中央控制节点与周围块区域之间的追踪关系.但是,单纯采取一次方式进行追踪难以有效的提高数据追踪精度,因此本文基于块融合的方式引入追踪阈值,采取削减判断的方式对式(9)所示的过程进行二次裁决,以便能够进一步的降低数据传输过程中存在的误差(见图3).
首先对不同块区域中的中央控制节点的数据传输能量进行排序,当本轮中央控制节点中获取的能量强度大于周围块区域中的中央控制节点的能量水平时,判定为满足能量阈值,该能量阈值E(r)获取方式如下:
E(r)=
(10)
其中,T为数据传输时间,r为追踪半径,PC为数据传输频率,Pr为当前中央控制节点的拓扑精确度,ηij定义同模型(9).


(11)
相应的ηij获取方式如下:
ηij=E′(k)
(12)
式(12)相关参数同式(7).
综合式(5)~(8),获取的追踪误差ωi为:
(13)
2 仿真实验
为验证本文算法的优越性,本文仿真采取MATLAB仿真环境将超混沌数据追踪算法(Hyper Chaos Data Tracking algorithm,HCDT算法)[11]设置为对照组比,在数据误码率、数据重传输频率、块区域抖动时间、误差修正时间四个指标上进行对比.具体仿真参数如表1所示:

图3 基于块融合误差的削减方法
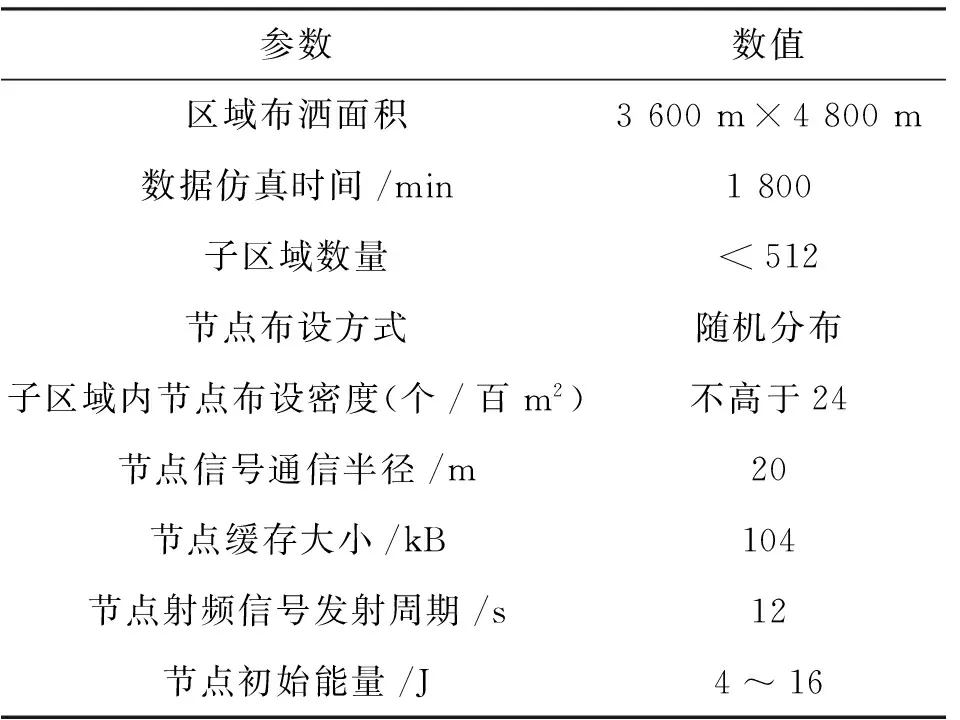
参数数值区域布洒面积3600m×4800m数据仿真时间/min1800子区域数量<512节点布设方式随机分布子区域内节点布设密度(个/百m2)不高于24节点信号通信半径/m20节点缓存大小/kB104节点射频信号发射周期/s12节点初始能量/J4~16
2.1 数据误码率
图4显示了本文算法同HCDT算法的数据误码率测试结果.由图4可知,本文算法与HCDT算法虽然都出现了数据误码率随着节点初始能量的提高而不断增加,然而本文算法的数据误码率要显著低于对照组算法,这是由于本文算法采用基于块融合误差削减,能够通过块分割方式逐个区域内进行精度提升流程,可以有效的降低因中央控制节点信息交互不畅而导致的数据链路抖动问题;而HCDT算法采取HODV等单播方式进行传输链路筛选,一旦传输过程中出现数据链路抖动问题,将导致数据误码率出现显著的上升现象.
2.2 数据重传输频率
图5显示了本文算法同HCDT算法的数据重传输频率测试结果.由图5可知,本文算法的数据传输频率要显著低于HCDT算法,这是由于本文算法采取块融合机制,能够稳定不同区域块之间的数据传输链路,有效保障数据垮区域传输之间的稳定性能,因此数据重传输频率较低;HCDT算法由于采用扫描递归机制进行区域块之间的数据传输链路选择,每次扫描过程均需要对数据进行重传输,因此HCDT算法的数据重传输频率要高于本文算法,易导致区域块中央控制节点出现性能下降的现象.

图4 两种算法的数据误码率测试结果

图5 两种算法的数据重传输频率测试结果
2.3 块区域抖动时间
图6显示了本文算法同HCDT算法的块区域抖动时间的测试数据.由图6可知,本文算法的块区域抖动时间要显著低于HCDT算法,这是由于本文算法基于块融合机制,设计了矢量化追踪流程,能够有效的实现不同块区域间数据的有效交互,降低因数据链路抖动而导致的块区域抖动现象的发生;而HCDT算法未采取任何有效措施实现对块区域抖动现象的矫正,因此导致块区域抖动时间要高于本文算法.
2.4 误差修正时间
图7显示了本文算法同HCDT算法的误差修正时间的对比.由图7可知,本文算法的误差修正时间要显著低于HCDT算法,这是由于本文算法采用矢量化追踪流程,能够有效的提高误差追踪过程中的精确度,而HCDT算法仅仅采用一次追踪方式,当出现误差时需要在下一个传输周期内完成误差修正,因此导致误差追踪过程较为繁琐,提高了误差修正时间水平.
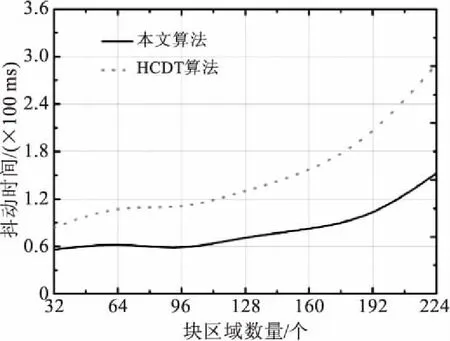
图6 两种算法的块区域抖动时间测试结果
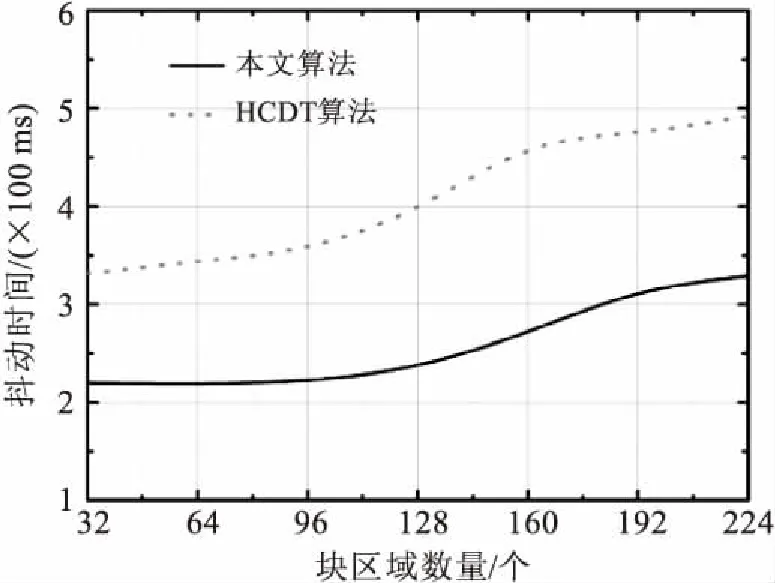
图7 两种算法的误差修正时间测试结果
3 结语
针对当前WSN误差追踪算法存在的追踪困难,数据抖动性能较差,以及块区域传输误差较高等难题,提出了一种基于块融合机制的WSN数据误差追踪算法,分别采取矢量化追踪机制及块融合误差削减方式,有效的改善了当前算法存在的若干不足之处,仿真实验证明了本文算法的有效性.
在后续的研究中,将针对本文算法仅能在节点固定情况下进行追踪的不足,采取超欧里几何平面映射机制,以便能够有效的适应各种复杂环境,进一步提高本文算法的有效性.
[1] ZHANG X,ZHU J.Identifying influential nodes in complex networks with community structure[J].Knowledge-Based Systems,2013,42(13):74-84.
[2] 邬厚民.无线传感网络中能量和距离改良的节点融合算法[J].中国测试,2012,38(5):62-66.
[3] GAO C,LAN X,ZHANG X G.A bio-inspired methodology of identifying influential nodes in complex networks[J].PloS One,2013,8(6):667-732.
[4] CHEN D,LV L,SHANG M S,et al.identifying influential nodes in complex networks[J].Physical A:Statistical Mechanics and its Applications,2011,391(4):1777-1787.
[5] ZHOU C,HE J W.A robust active queue management scheme for network congestion control[J].Computers and Electrical Engineering,2013,39(1):285-293.
[6] 王文吉.基于能量因素的无线传感网络关键节点定位算法[J].电子与信息学报,2014,36(7):1728-1734.
[7] HABIB M,AMMARI,SAJAL K DAS.A study of K-coverage and measures of connectivity in wireless sensor networks[J].IEEE Transactions on Computers,2013,59(2):258-267.
[8] HA L E,LI J,YUAN G.A TCP Performance Enhancement Scheme in Infrastructure based on Vehicular Networks[J].China Communications,2015,6(13):73-84.
[9] HAO X C,JIA N,LIU B.Multi-path optimizing routing protocol based on predicting congestion for wireless sensor network[J].Journal of Electronics & Information Technology,2011,33(5):1261-1265.
[10] WANG L,GENG X.A community-driven hierarchical message transmission scheme in opportunistic networks[J].Smart Computing Review,2011,1(1):85-94.
[11] WANG D,ZHANG Q,LIU J C.Partial network coding:theory and application for continuous sensor data collection[J].In Proc.of the 14th IEEE International Workshop on Quality of Service,2012,35(10):93-10.
