基于改进多输出支持向量机的声发射源定位研究*

朱 军，史 勃，张环宇，荣胜波，黄益泽

(中国科学院 沈阳自动化研究所，辽宁 沈阳 110000)

0 引 言

声发射(acoustic emission，AE)现象[1]的活动性能够表征煤岩体受载、变形及破坏的状态及发展过程。故声发射监测可以预测煤与瓦斯突出点的位置[2]，AE源的定位对于煤岩体破裂情况的分析具有重要意义。传统的定位方法大多基于AE速度和时间的一些算法如时差定位法[3]、模态AE定位[4]以及能量定位[5]。而煤矿生产环境复杂，为了提高定位的准确性，出现了基于统计学习理论的定位方法[6]和基于特征匹配的算法[7,8]，如神经网络、支持向量机(support vector machine,SVM)、加权K均值算法等[9]，其中，SVM的定位精度相比于神经网络有了更大的提升[10]，所需采集的样本也相对较少，但其参数调节比较困难。

为了改善AE定位的效果，结合核主成分分析(kernel principal component analysis,KPCA)提出了一种改进的多输出最小二乘SVM(least squares SVM,LSSVM)的定位算法(KPCA-LSSVM)。采用KPCA对采集信息进行处理，提取多路信号中对应时间延迟的特征，采用多输出LSSVM对特征向量与位置信息之间的关系进行拟合，得到对应的AE源位置,将该方法应用于煤矿瓦斯突出灾害的预测，仿真试验结果表明：本文方法能够获得更高精度的定位结果，提高了定位效率。

1 KPCA-LSSVM定位算法

1.1 KPCA

KPCA的处理过程如下：

k(xi,xj)=φT(xi)φ(xj)

(1)

其中，假定已经进行了数据预处理过程，使得训练样本的所有特征向量满足零均值条件，即

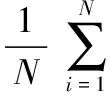
(2)

2)求解特征子空间坐标

Kα=λα

(3)

式中λ为K的特征值；α为对应的子空间基向量。

3)特征向量的选取

计算投影

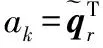
(4)

式中ar,j为基向量αr的第j个元素。

1.2 多输出SVM回归

多输出SVM回归是针对系统回归函数的因变量y(为一个向量，即y∈Rk,k>1)而提出的一种新的SVM算法，图1为定位模型框图，用定义在超球上的损失函数代替定义在超立方体上的损失函数，损失函数如下

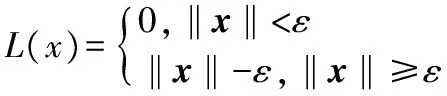
(5)

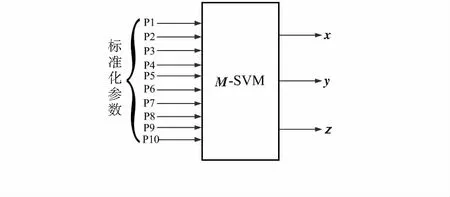
图1 多输出SVM定位模型

对于M维输入，N维输出的函数拟合问题，设训练样本集

{(xi,yi)},i=1,2,…,L,xi∈RM,yi∈RN

可以构造回归函数

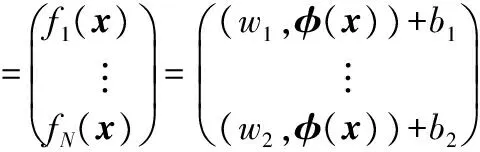
=(W,φ(x))+B

(6)

式中W=(w1,w2,…,wN);B=(b1,b2,…,bN)。该回归问题等价于不等式约束下的极值问题

(7)

式中ui=‖ei‖,ei=yi-(W,φ(xi))+B。根据KKT条件及对偶原理，上述问题转化为求极值问题

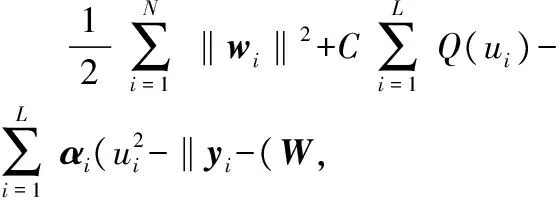
(8)

为了求取上述函数的极值，分别对wi,bi,ui,αi求偏导数并令偏导值等于0,即

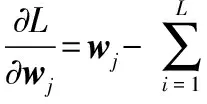
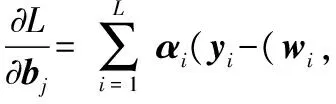
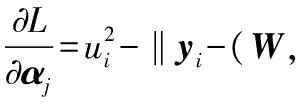
(9)

可得到

(10)

(11)

式中Φ=[φ(x1),…，φ(xL))]T,Dα=diag{α1,…,αL},A=[α1,…,αL]T,I=[1,…，1]T。

相比单维输出情况下的最优化问题要该求极值问题更复杂，应采用特殊的迭代法求解，操作方法如下：

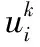
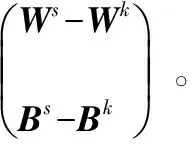
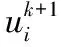
1.3 文化基因优化算法

为了避免前述算法落入局部最优，采用文化基因算法(memetic algorithm,MA)进行改进，将局域搜索和遗传算法相结合，兼顾了局部搜索算法的深度优势和群体算法搜索面积大的优点 ，交叉和变异运算如下

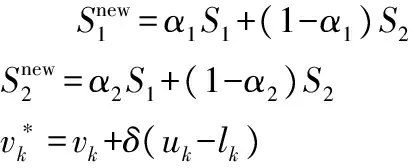
(12)

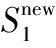
SVM的准确度依赖于学习机外部参数，针对最优参数确定的问题，MA使用的SVM外部参数有C和ε，根据适应度从变异后的种群中选择G个新个体作为下一代，本文选用均方差作为适应度函数，其表达式如下

(13)

2 试验平台与AE信号的产生

AE试验平台如图2所示。采集AE信号如图3所示。选取振铃计数、事件计数、幅度、能量计数、上升时间、持续时间、有效值电压和平均值电压8个参数，试验平台为5路传感器信号，故生成了维度为40的输入向量。

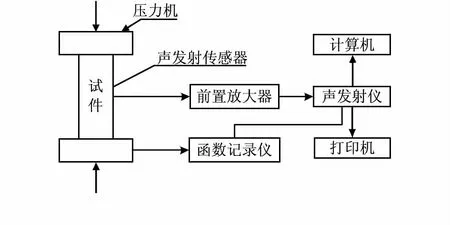
图2 AE试验平台示意

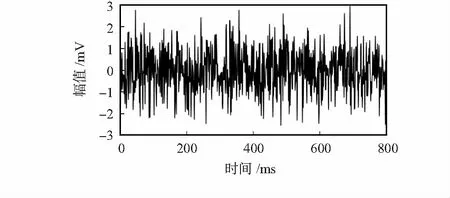
图3 典型的连续型AE信号

3 试验结果与分析

基于KPCA-LSSVM的AE定位算法的框架如图4。

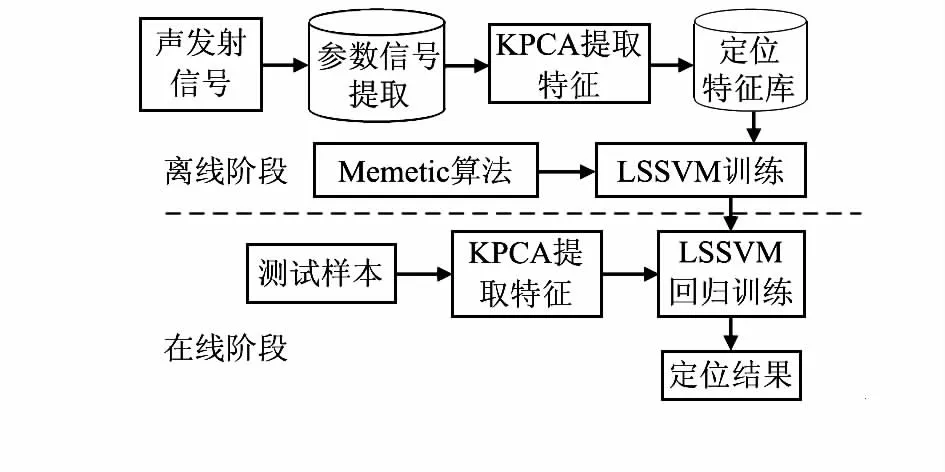
图4 KPCA-LSSVM算法框架

每次采集数据并生成一个40维的输入向量，在离线阶段收集多组数据，首先进行归一化处理，KPCA中选择高斯径向基和函数。对式(2)的求解，采用奇异值分解(singular value decomposition,SVD)方法。试验发现，当σ2=1 900时，特征提取的效果比较好，前10个特征参数的贡献率之和超过95 %，因而输入向量由40维变为10维。其前20个特征的贡献率分布如图5所示。

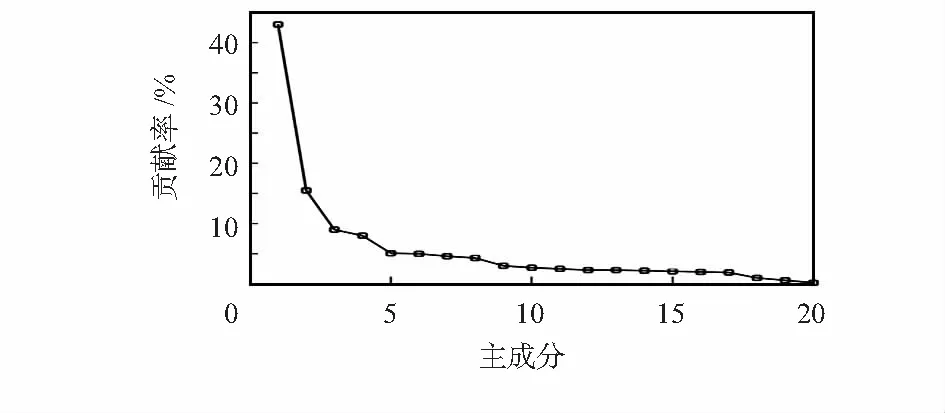
图5 核矩阵中前20个成分的贡献率

为了验证算法的性能，在一次试验中，采集了100组离线数据，通过训练并在线测试了一些AE点。结果如表1。

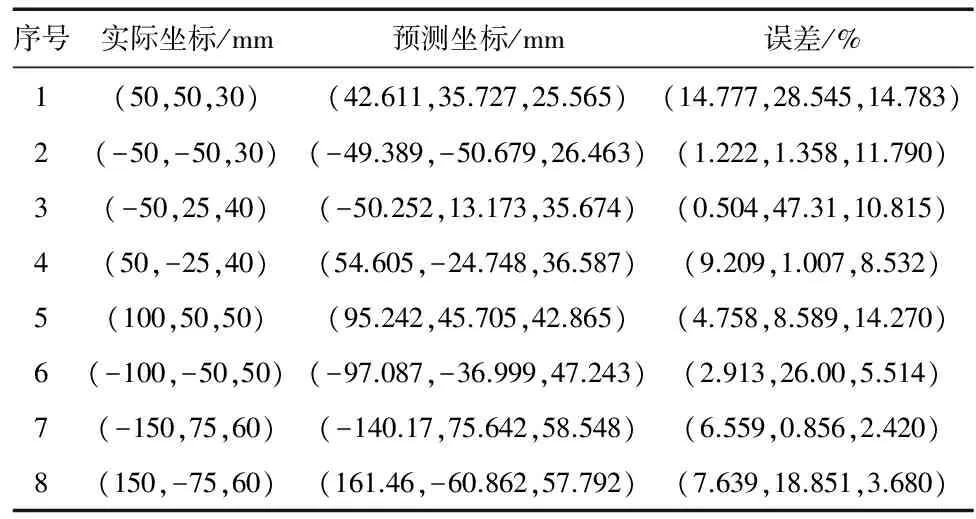
表1 定位结果

为了验证KPCA-LSSVM的AE定位优越性，与传统的PCA-LSSVM(手动方式确定LSSVM参数)、PCA-GA-LSSVM(GA算法优化LSSVM参数)进行对比测试，采用定位误差和平均定位误差对AE定位结果进行评价，公式为

(14)

(15)

式中n为测试点的数量。

采用LSSVM拟合特征向量与地理位置信息之间的关系时，参数C和ε的选择至关重要，采用PCA-LSSVM和PCA-GA-LSSVM以及KPCA- LSSVM进行定位试验，参数如表1所示。定位比较结果如图6所示，可以得出：相比于其他两种方法，KPCA-LSSVM的定位精度有一定程度的提高，因为GA，MA算法可以找到更加合理的LSSVM参数C和ε的值，建立的LSSVM可以更好拟合特征向量与位置信息之间的映射关系，定位结果更加可靠。

为了比较各种方法进行AE定位的训练速度，仿真统计PCA-LSSVM、PCA-GA-LSSVM和KPCA -LSSVM的运行时间，结果如表2。从训练结果可知：PCA-LSSVM最快，减少了寻优的过程，但是其设置参数无法准寻一定的规律，

具有经验性，其定位精度也无法保障，没有普遍适用性，而KPCA-LSSVM的训练效率要高于PCA-GA-LSSVM,定位的实时性更优，更符合AE定位的要求。

4 结 论

针对煤矿中煤与瓦斯突出灾害，提出了一种基于KPCA-LSSVM的AE定位算法，该算法采用KPCA提取声发射参数信息中对定位结果贡献重要的特征，对数据进行一定的降维压缩，从而降低了LSSVM的复杂度，最后采用LSSVM拟合特征与位置信息的非线性关系，并采用Memetic算法搜索LSSVM的最优参数，试验结果表明：KPCA-LSSVM的定位精度要高于传统算法，并且运行时间相比同级别算法更具优势。

[1] 曾宪涛,姜耀东,王宏伟,等.单轴压缩条件下煤岩体声发射特性研究[J].煤炭工程,2015,47(2):75-77.

[2] 涂庆毅,程远平,王 亮,等.煤与瓦斯突出的动态过程研究[J].煤炭科学技术,2015,43(6):71-75.

[3] 于 洋,王 赛.一种新的声发射时差定位方法[J].化工自动化及仪表,2015,42(10):1127-1130.

[4] 张维刚,李凯丽,肉孜麦麦提,等.金属薄板中导波的模态识别和波速测定[J].声学技术,2015(4):322-326.

[5] 刘艳芳,张会芝,王鲜芳.改进的基于能量的声源定位算法[J].计算机工程与设计,2015(7):1976-1980.

[6] 蔡朝晖,夏 溪,胡 波,等.室内信号强度指纹定位算法改进[J].计算机科学,2014,41(11):178-181.

[7] 马 豪,尹健龙,李东升.基于小波分解的磨床声发射特征信号提取方法[J].传感器与微系统,2016,35(7):13-15.

[8] 张会清,石晓伟,邓贵华,等.基于BP神经网络和泰勒级数的室内定位算法研究[J].电子学报,2012,40(9):1876-1879.

[9] Van Laarhoven T,Marchiori E.Local network community detection with continuous optimization of conductance and weighted kernel K-means[J].Journal of Machine Learning Research,2016,17(1):5148-5175.

[10] Ghamisi P,Couceiro M S,Benediktsson J A.A novel feature selection approach based on FODPSO and SVM[J].IEEE Transactions on Geoscience & Remote Sensing,2015,53(5):2935-2947.