独斜塔斜拉桥地锚箱几何参数敏感性分析

周水兴，汪 林

(重庆交通大学 土木工程学院，重庆 400074)

0 引 言

斜拉桥以可调的结构受力体系，合理的经济性及优美造型等特点而具有强大生命力[1]，但主要以自锚体系为主，地锚或部分地锚体系相对偏少，因为地锚工程浩大、造价昂贵，在一定程度上制约了地锚式斜拉桥的发展。但相对全自锚式斜拉桥，成桥状态下部分地锚式斜拉桥具有诸多优点[2]，我国对地锚式和部分地锚式斜拉桥的研究都很少，20世纪90年代初才开始跟踪国外地锚式斜拉桥的研究，并思索在我国斜拉桥的应用[3- 4]。地锚作为地锚式斜拉桥中最重要的构造，按结构形式一般可分为岩锚、实体重力式锚、空腔式箱形锚(地锚箱)和钻孔桩锚4种。岩锚主要利用天然岩石的抗剪能力，采用竖、斜井和岩槽的形式将锚锭埋入岩石中，对地质条件要求比较高；实体重力式锚是利用圬工体积的自重平衡拉索的拉力；空腔式箱形地锚是实体重力式的演化，原理与重力式锚基本一致，不同的是将实体内部变为一个个腔室，腔内填充砂、石、土作为压重；钻孔桩锚的受力特点是利用桩的摩擦力和嵌岩力抵抗拉索的拉力[5]。国内第一座地锚式斜拉桥——郧阳汉江公路大桥，地锚构造采用的是空腔式箱形锚；岷江源兴川大桥的地锚型式因其地锚索少而采用实体重力式锚；沈阳市蒲河盛京桥地锚采用半重力中空异型箱体，箱体1/3埋入地下，箱体承台下采用钻孔灌注桩基础[6-8]。地锚箱既具有实体重力式锚的优点，又能减少造价和工程量，同时还可以和钻孔桩相结合，能适应各种地质条件。相信在不久的将来，在地锚式斜拉桥中采用地锚箱构造的会越来越多，但目前对地锚箱的相关研究却非常少，地锚箱各尺寸参数的取值直接关系到拉索的锚固段受力是否合理，进而影响索力甚至桥梁安全。笔者以芙蓉江大桥地锚箱设计为研究对象，针对其几何参数进行敏感性分析，为以后相关设计提供参考。

1 工程背景

芙蓉江大桥为国内首座地锚式独斜塔预应力混凝土斜拉桥(图1)。芙蓉江大桥的地锚构造采用地锚箱形式，地锚箱的基本断面是单箱三室箱型截面(图2)，箱体采用C40混凝土，顶面全宽24.5 m。近塔侧锚室箱梁中心线处高7 m，远塔端侧锚室中心线处高10 m。地锚箱中间设置两道0.6 m的横隔板，锚室中间两道腹板厚均为1.2 m，边腹板厚均为0.7 m，顶板厚0.7 m，底板厚1.5 m。中间锚室为斜拉索锚固区，锚索端构造采用凸齿式，地锚箱斜拉索标准间距为1.65 m。考虑受力的需要，在锚室内填充C15片石混凝土作为恒载压重，但不参与结构受力。箱体全部埋入地下，地锚箱所处地形平坦，上覆坡残积黏土、碎石土，覆盖层下部发育一层溶蚀破碎带，下部为完整基岩，工程地质条件良好。

图1 芙蓉江大桥的立面布置(单位：cm)Fig. 1 Layout of façade of Furong River Bridge

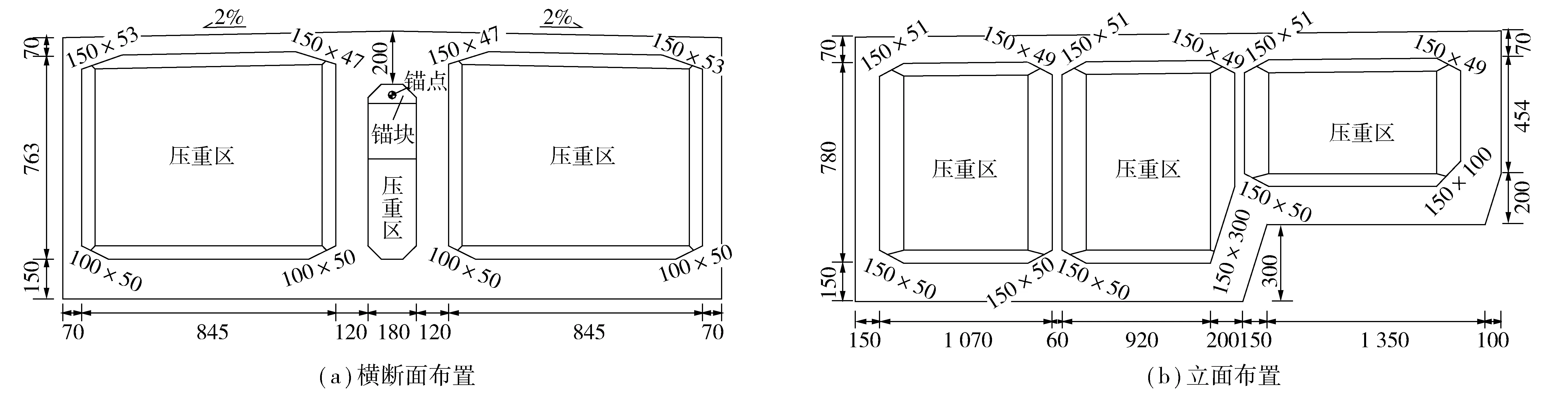
图2 地锚箱标准断面(单位：cm)Fig. 2 Standard section of the ground anchor-box

2 理论分析

地锚箱作为拉索的锚固结构，局部受力非常复杂，尤其是在直接承受索力作用的锚固区顶板处。在设计过程中一般需要反复调整箱型结构尺寸，以使锚固区顶板受力合理。通过结构力学简化计算，可以在宏观上了解各参数对锚固区顶板应力的影响情况，方便设计者在对箱型结构尺寸进行调整时能快速把握方向。

2.1 力学模型

地锚箱在受斜向索力作用时，锚固区顶板是受力最不利的位置，为分析地锚箱几何参数对锚固区顶板受力的影响，沿地锚箱长度方向取单位长度1 m，将其简化成刚架结构，如图3虚线，斜拉索竖向分力用2P表示。

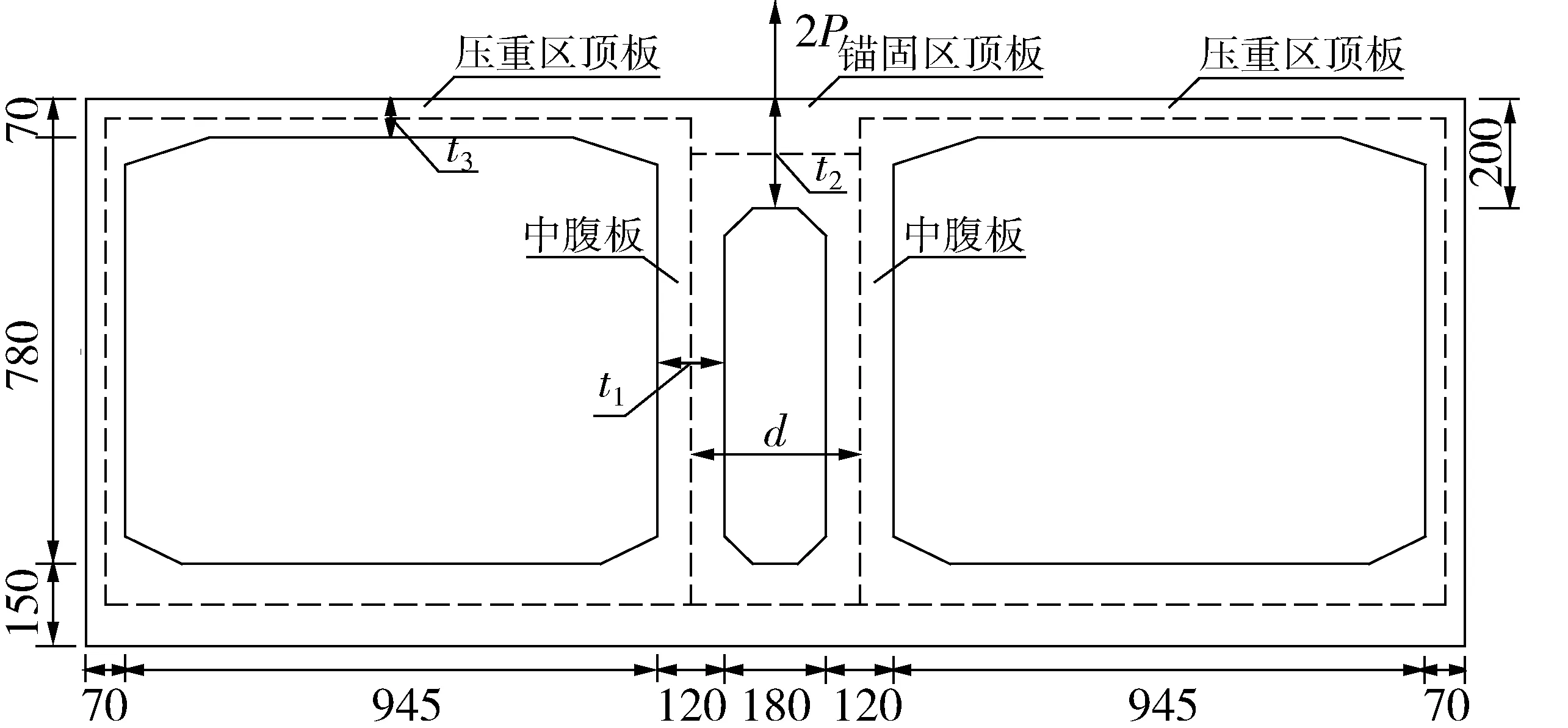
图3 刚架结构模型(单位：cm)Fig. 3 Rigid frame structural model

底板承受片石混凝土压重，且和大地连在一起，可以在刚架底部采用固结形式。因为整个刚架结构为对称形式，且承受对称荷载作用，故可取半边结构体系进行受力分析，如图4(a)。若按原设计取值，则有L1=8.9 m，L2=10.4 m，L3=1.5 m，L4=0.65 m。

忽略轴向变形，采用位移法求解，基本未知量为刚节点B、C、D的转角θB、θC、θD和刚节点B、C的水平位移Δ，如图4(b)。

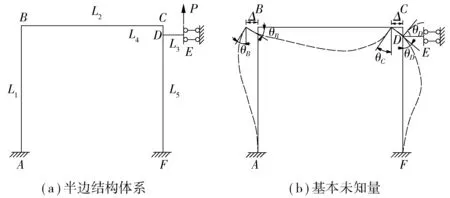
图4 简化计算图示Fig. 4 Simplified calculation diagram

由结构力学相关知识得到式(1)，可以求出θB、θC、θD、Δ。I为惯性矩，i为线刚度：

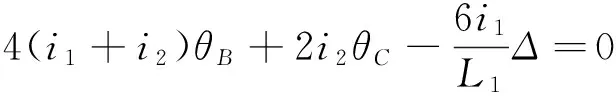
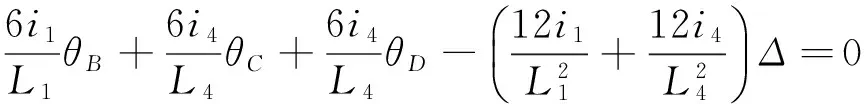
(1)

然后根据式(2)求出MED，进而可以求出由弯矩在图4中E点截面上缘产生的正应力(对应锚固区顶板应力)：

(2)

(3)

2.2 参数分析

利用式(1)～式(3)可以分别建立锚固区顶板应力σ分别与地锚箱中腹板间距d、中腹板厚度t1、锚固区顶板厚度t2、压重区顶板厚度t3的关系。下面以中腹板间距为例加以说明。

当中腹板间距为d时，结合图3、图4可得此时各杆件的各种参数，见表1。

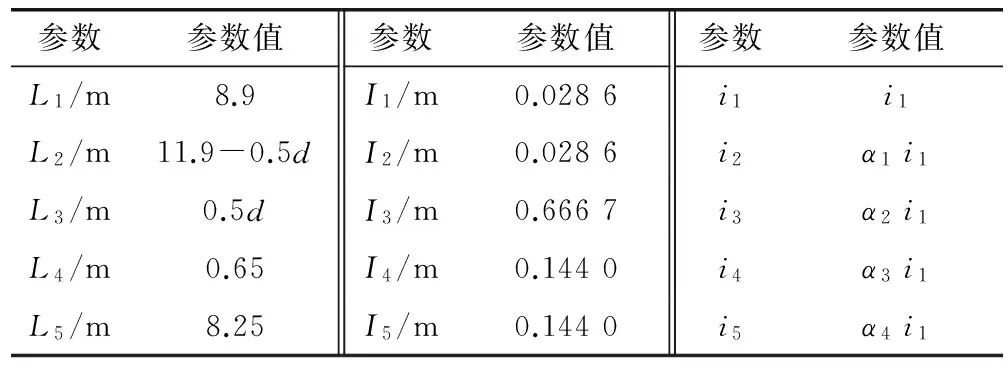
表1 杆件参数Table 1 The bar parameter

将表1中各参数代入式(1)得：

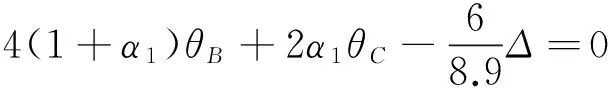
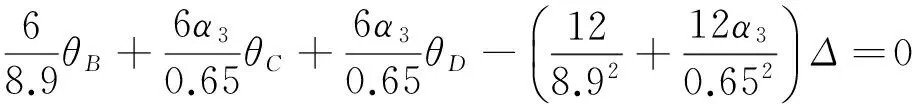
(4)

其中：

从式(4)求出θD并代入式(2)中求出MED：

(5)

从而可以得到：

(6)

代入α1、α2、α3、α4数值，由式(4)～式(6)，可得σ与中腹板间距d的函数关系式σ=Pf(d)。这里主要关注σ随中腹板间距d的变化趋势，取P=100t，用MATLAB绘制σ与d的关系曲线，如图5。

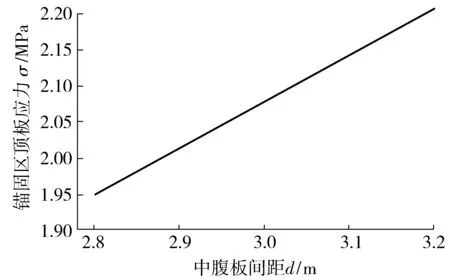
图5 中腹板间距d对锚固区顶板应力σ的影响曲线Fig. 5 The influence curve of the middle web plate spacing (d) on the stress of roof in the anchorage zone (σ)

与上同理可以分别得到中腹板厚度t1、锚固区顶板厚度t2、压重区顶板厚度t3对锚固区顶板应力σ的影响曲线，如图6。

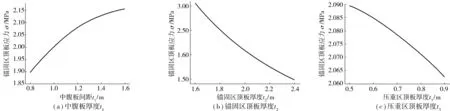
图6 中腹板厚度t1、锚固区顶板厚度t2、压重区顶板厚度t3对锚固区顶板应力σ的影响曲线Fig. 6 The influence curve of the middle web plate thickness (t1)，the roof thickness of the anchorage zone (t2) and the thickness of the top plate in the compression zone (t3) on the stress of roof in the anchorage zone (σ)

3 有限元分析

3.1 边界条件

采用以下3种边界条件形式进行有限元试算，通过比较分析，选取比较合理的边界模拟方式。

1) 完全固结形式；

2) 建立部分土体单元分析；

3) 采用只受压弹簧单元模拟岩土作用。

地锚箱附近土体为中风化灰岩，天然密度为2.75 g/cm3，抗压强度标准值为87.2 MPa。参照《工程地质手册》[9]，岩土弹性模量取38 500 MPa，弹簧单元的地基反力模量取1 015 MN/m3，在建立部分岩体时，地锚箱边界土体范围取各自3倍长度[10]，地锚箱采用C40混凝土，计算容重取27.05 kN/m3。

在有限元模型中，片石混凝土压重换算成面荷载施加，索力以垂直锚块方向的面荷载施加，预应力钢束采用钢筋单元模拟。锚固区索孔之间顶板处应力可以反映锚固段受力特征，故可取每两个索孔之间中点位置作为应力提取点(图7)，比较3种不同边界下锚固区顶板的应力情况(图8)。

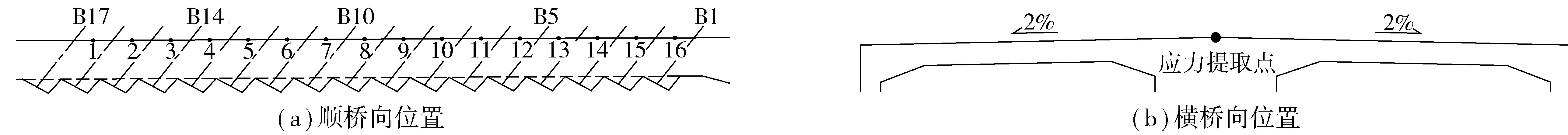
图7 锚固区顶板应力提取点位置Fig. 7 Extraction point position of roof stress in anchorage zone

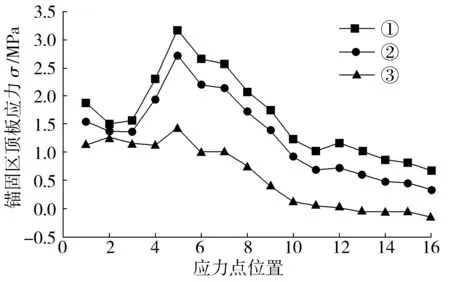
图8 不同边界条件下锚固区顶板应力Fig. 8 The roof stress of anchorage zone under different boundary conditions

由图8可知，3种不同边界下锚固区顶板应力变化趋势基本一致，边界1和边界2的计算结果比较接近。由于只考虑其垂直面方向的约束，忽略了其横向约束，导致边界3计算结果偏小。实际上地锚箱与岩体接触部分节点会发生微小位移，不可能完全固结。因此，采用边界1得到的结果是其上限，采用边界3是其下限，边界2更接近真实情况。

故在用有限元方法对地锚箱进行几何参数敏感性分析时，采用建立部分土体单元的边界2。岩土和地锚箱接触部分采用共节点处理，岩土边界采用全固结形式。因未考虑锚垫板和构造钢筋，故不关心应力数值的大小，仅关注其变化趋势。同时为减少干扰，下面计算并未记入预应力钢筋作用。

3.2 参数分析

3.2.1 中腹板间距的影响

分别取中腹板间距为2.8、2.9、3.0(设计值)、3.1、3.2 m，其它的尺寸参数均取用设计值，建立有限元模型(图9)。

采用对比分析的方法，对5种不同中腹板厚度的有限元模型的计算结果进行分析，随着中腹板厚度的变化，锚固区顶板应力的变化存在一定规律性，中腹板间距对锚固区顶板应力影响的计算结果如图10。

图9 地锚箱有限元模型Fig. 9 Finite element model of ground anchor-box

图10 中腹板间距对锚固区顶板应力影响曲线Fig. 10 The influence curve of the middle web plate spacing on the stress of roof in the anchorage zone

由图10(a)可知，5种不同中腹板间距下的锚固区顶板应力变化趋势基本一致，中腹板间距变化对锚固区顶板应力的影响呈现一定的规律性，在应力点3～10位置处，规律性尤其明显，因为这些位置是处于整个锚固区顶板的中间部位，承受的索力比较大。同时可以看出，随着中腹板间距的增大，锚固区顶板的应力呈现逐渐递增的趋势，应力点3～10位置处的递增趋势非常明显，如图10(b)。同时可以发现，随着中腹板间距的增加，锚固区顶板应力有呈线性增加的现象，与理论分析中图5吻合一致。中腹板间距增加，使得锚固区横向跨度变大，横向应力增加，故会导致锚固区顶板应力增大。

3.2.2 中腹板厚度的影响

分别取中腹板厚度为0.8、1.0、1.2(设计值)、1.4、1.6 m建立有限元模型，其它的尺寸均取设计值，对5种不同中腹板厚度的有限元模型的计算结果进行分析。随着中腹板厚度的变化，锚固区顶板应力的变化存在一定的规律性。中腹板厚度对锚固区顶板应力影响的计算结果如图11。

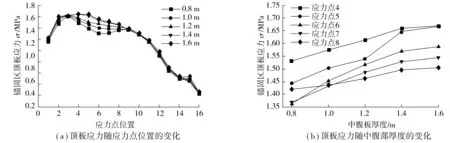
图11 中腹板厚度对锚固区顶板应力影响曲线Fig. 11 The influence curve of the middle web plate thickness on the stress of roof in the anchorage zone

由图11(a)可知，5种不同中腹板厚度下的锚固区顶板应力变化趋势基本一致，在应力点4～8位置处，中腹板厚度的变化对其应力的影响比较明显，在其它应力点位置处，中腹板厚度的变化对其应力的影响较小。因为应力点4～8位置处的索力都很大，其它位置处较小，在索力较大位置，锚固区顶板应力对中腹板厚度这一参数比较敏感。同时可以看出，应力点4～8位置处的应力值随着中腹板厚度的增大而有所增大，并且随着中腹板厚度的增大，各点应力的增大幅度逐渐变缓，如图11(b)，与理论分析中图6(a)吻合一致。中腹板厚度增大，进一步加强了对锚固区顶板两侧的约束，限制了锚固区顶板应力向压重区顶板的传递，从而随着中腹板厚度的增大，锚固区顶板的应力逐渐增大。

3.2.3 锚固区顶板厚度的影响

锚固区顶板直接承受斜拉索力的作用，其受力情况与它的厚度存在一定的关系，为了研究锚固区顶板厚度对地锚箱应力的影响，分别取地锚箱锚固区顶板厚度为1.6、1.8、2.0(设计值)、2.2、2.4 m，其它尺寸参数均取用设计值，建立有限元模型。对5种不同锚固区顶板厚度的有限元模型的计算结果进行分析，随着锚固区顶板厚度的变化，锚固区顶板应力的变化存在一定的规律性。锚固区顶板厚度对锚固区顶板应力影响的计算结果如图12。

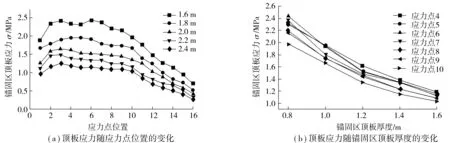
图12 锚固区顶板厚度对锚固区顶板应力影响曲线Fig. 12 The influence curve of the roof thickness of the anchorage zone on the stress of roof in the anchorage zone

由图12(a)可知，5种不同锚固区顶板厚度下的锚固区顶板应力变化趋势基本一致，在各个应力点处，锚固区顶板厚度的变化对锚固区顶板应力的影响呈现出明显的规律性。随着锚固区顶板厚度的增加，锚固区顶板应力逐渐减小，并且随着锚固区顶板厚度的增加，锚固区顶板应力减小的梯度有逐渐变小的趋势，如图12(b)，与理论分析中图6(b)吻合一致。锚固区顶板厚度的增大，使锚固区顶板的刚度增大，在其它条件不变的情况下，整个顶板应力的分布主要取决于锚固区顶板与压重区顶板的刚度比值，故当锚固区顶板厚度增大时，锚固区顶板的应力减小。

3.2.4 压重区顶板厚度的影响

分别取压重区顶板厚度为0.5、0.6、0.7(设计值)、0.8、0.9 m，其它的尺寸均取设计值，建立有限元模型。对5种不同压重区顶板厚度的有限元模型的计算结果进行分析，压重区顶板厚度对锚固区顶板应力影响的计算如图13。

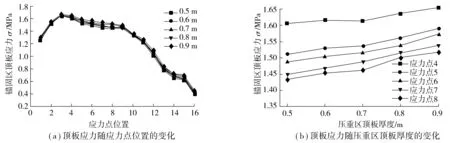
图13 压重区顶板厚度对锚固区顶板应力影响曲线Fig. 13 The influence curve of the thickness of the top plate in the compression zone on the stress of roof in the anchorage zone

由图13(a)可知，5种不同压重区顶板厚度下的锚固区顶板应力变化趋势基本一致，可以看出，压重区顶板厚度的变化对压重区顶板应力的影响并不大，但是从图13(b)还是可以看出，随着压重区顶板厚度的增大，锚固区顶板的应力有增大的趋势，但是增大得非常小。压重区顶板厚度增大，使压重区顶板的刚度增大，锚固区顶板与压重区顶板的刚度比值减小，故压重区顶板厚度增大会使锚固区顶板应力有增大的趋势。同时，索力作用在锚固区，压重区顶板应力本身比较小，且又有中腹板在锚固区顶板和压重区顶板之间，相当于在锚固区顶板和压重区顶板之间有些许阻隔，导致两者之间的相互影响不大，即压重区顶板厚度的变化对锚固区顶板应力的影响较小。

4 敏感性程度分析

标准离差率是衡量资料中各观测值离散程度的相对指标，可以消除单位和平均数不同的影响[11]，为分析锚固区顶板应力对中腹板间距、中腹板厚度、锚固区顶板厚度和压重区顶板厚度4个参数的敏感性程度大小，在标准离差率的基础上考虑各参数改变量的改变程度影响，定义一个敏感性系数k来表征敏感性程度：

(7)

式中：x为参数的设计值；y为参数取设计值x对应的应力值；yi为参数取值xi对应的应力值；n为参数取值的数量；Δx为参数的改变量。

按式(7)可以得到锚固区顶板应力对各个参数的敏感性系数值，如表2～表5。

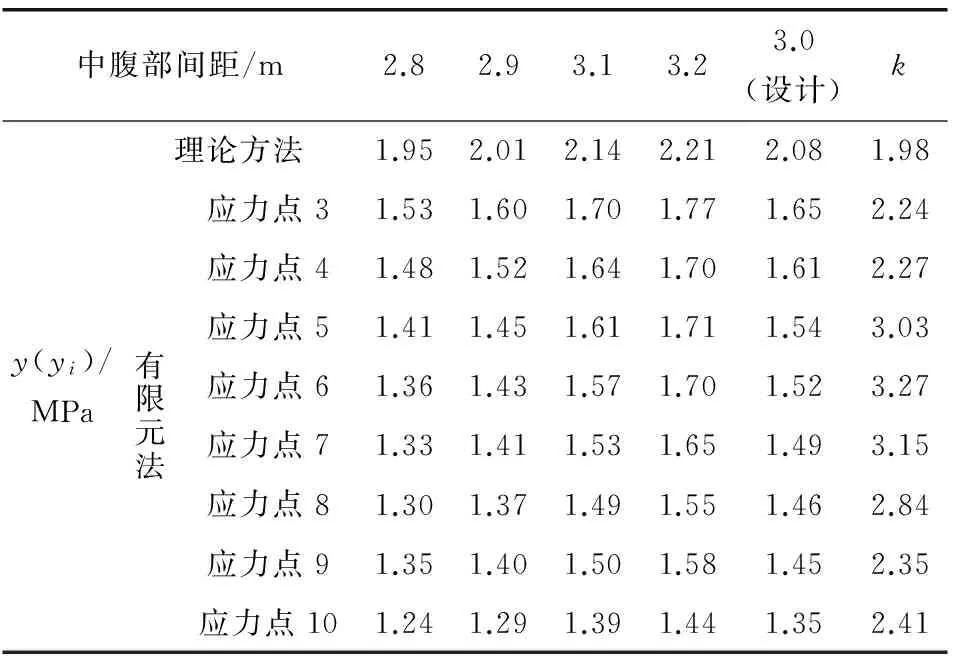
表2 中腹板间距敏感性Table 2 Sensitivity of the middle web spacing

表3 中腹板厚度敏感性Table 3 Sensitivity of the middle web plate thickness

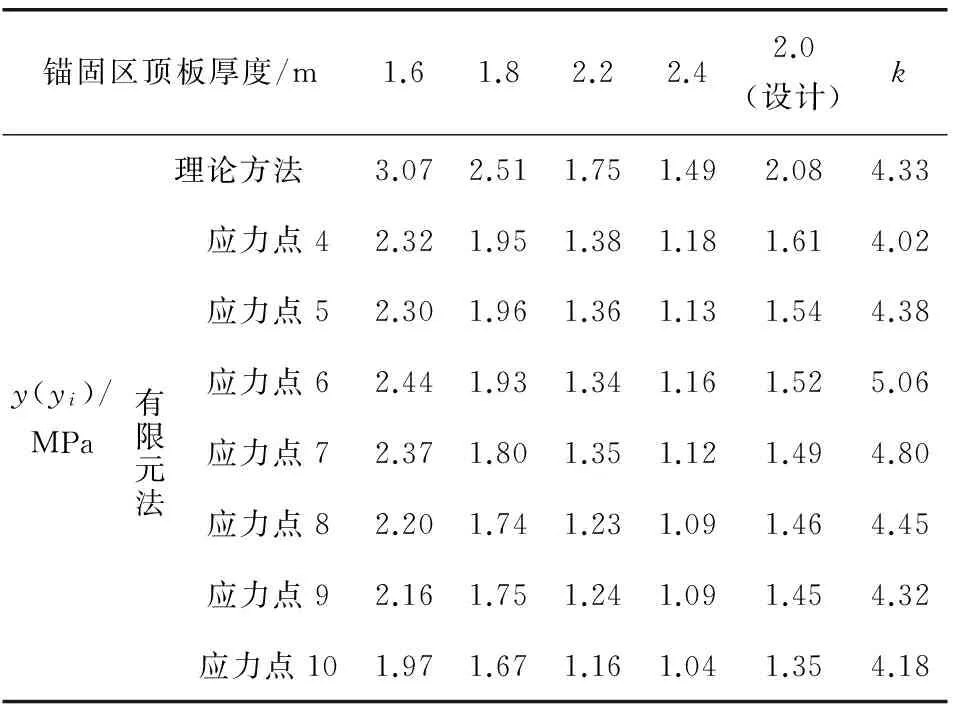
表4 锚固区顶板厚度敏感性Table 4 Sensitivity of roof thickness of the anchorage zone

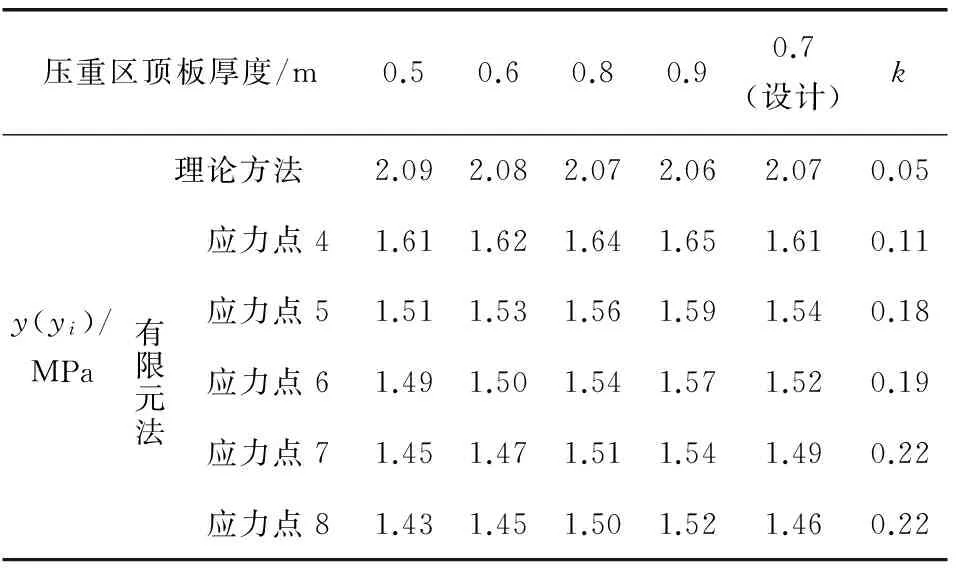
表5 压重区顶板厚度敏感性Table 5 Sensitivity of thickness of the top plate in the compression zone

由表2～表5可知，锚固区顶板应力对中腹板间距、中腹板厚度、锚固区顶板厚度和压重区顶板厚度的敏感性系数，理论值依次是1.98、0.46、4.33、0.05，有限元值依次是2.69、0.40、4.46、0.18(平均值)。可以看出，理论和有限元结果都表明：敏感性程度由大到小依次是锚固区顶板厚度、中腹板间距、中腹板厚度、压重区顶板厚度。

5 结 论

将地锚箱空间问题运用杆系结构简化成平面杆系刚架，运用结构力学知识并结合MATLAB，得到了各个几何参数对锚固区顶板应力影响曲线，运用Midas-FEA探讨了地锚箱边界条件的模拟方式，研究了几何参数对锚固区顶板应力的影响，得到如下几点结论：

1) 在对地锚箱边界条件进行模拟的时候，建立地锚箱周围部分土体得到的结果更为可靠。

2) 中腹板间距、中腹板厚度、锚固区顶板厚度、压重区顶板厚度对锚固区顶板应力有一定影响，尤其在索力较大的位置处，对锚固区顶板处应力的影响有一定的规律性。就敏感性程度而言，由大到小依次为：锚固区顶板厚度、中腹板间距、中腹板厚度、压重区顶板厚度。

3) 采用简化的力学模型分析，在中腹板间距、中腹板厚度和锚固区顶板厚度对锚固区顶板应力影响趋势方面和有限元分析得到的结果基本吻合一致，压重区顶板厚度影响趋势与有限元分析的有所出入。在对锚固顶板应力影响敏感性方面理论分析和有限元分析完全一致。

[1] 蒲黔辉，赵虎.边中跨比及无索区长度对独塔斜拉桥静动力影响[J] 重庆交通大学学报(自然科学版)，2013，32(6)：1101-1105.

PU Qianhui，ZHAO Hu.Influence of ratio of side-span to mid-span and length of unsupported deck on static and dynamic performance of single pylon cable-stayed bridges[J].JournalofChongqingJiaotongUniversity(NaturalScience)，2013，32 (6)：1101-1105.

[2] ZHANG L W，XIA R J.The reasonable finished dead state research of partially earth-anchored cable-stayed bridge[J].AdvancedMaterialsResearch，2011，255-260：1319-1325.

[3] 王福春.预应力混凝土折线塔斜拉桥力学特性的研究[D].沈阳：东北大学，2011.

WANG Fuchun.StudyofMechanicsCharacteristicsofCable-stayedBridgewithPolygonalLineTowerofPrestressedConcrete[D].Shenyang：Northeastern University，2011.

[4] 裴炳志，叶见曙，汪剑.地锚式斜拉桥收缩徐变效应测试与分析[J].桥梁建设，2008 (6)：25-29.

PEI Bingzhi，YE Jianshu，WANG Jian.Measurement and analysis of shrinkage and creep effect of a ground anchored cable-stayed bridge[J].BridgeConstruction，2008(6)：25-29.

[5] 宋继宏.郧阳汉江公路大桥地锚的设计与施工[C] //全国城市桥梁青年科技学术会议论文集.上海：中国土木工程学会，1996：490- 494.

SONG Jihong.Design and construction of ground anchor of Yunyang Hanjiang Highway Bridge[C] //ProceedingsoftheNationalConferenceonyoungtechnologyforUrbanBridges.Shanghai：China Civil Engineering Society，1996：490- 494.

[6] 王吉仁.郧阳汉江公路大桥设计与施工[J].公路，1996(3)：15-20.

WANG Jiren.Design and construction of Yunyang Hanjiang Highway Bridge[J].Highway，1996(3)：15-20.

[7] 杨善红.岷江源兴川大桥结构与造型设计[J].工程与建设，2011，25(5)：637-641.

YANG Shanhong.Structure and form design of Yuanxingchuan Bridge in Minjiang River[J].EngineeringandConstruction，2011，25(5)：637-641.

[8] 李洋.沈阳市蒲河盛京斜拉桥设计[J].北方交通，2014(11)：41- 43.

LI Yang.The design of Shenyang City Puhe River Shengjing Cable-Stayed Bridge[J].NorthernCommunications，2014(11)：41- 43.

[9] 常士骠，张苏明，项渤，等.工程地质手册[M].第四版.北京：中国建筑工业出版社，2007：169-170.

CHANG Shibiao，ZHANG Suming，XIANG Bo，et all.HandbookofEngineeringGeology[M].4th ed.Beijing：China Architecture & Building Press，2007：169-170.

[10] 苏晓堃.隧道开挖数值模拟的围岩边界取值范围研究[J].铁道工程学报，2012(3)：63-68.

SU Xiaokun.Research on choosing boundary range of surrounding rock in numerical simulation of tunnel excavation[J].JournalofRailwayEngineeringSociety，2012(3)：63-68.

[11] 谢艳梅.混合梁连续刚构桥结构几何参数优化研究[D].成都：西南交通大学，2013：7-8.

XIE Yanmei.OptimizationStudyofStructuralGeometricalParametersofHybrid-GirderRigid-FrameBridge[D].Chengdu：Southwest Jiaotong University，2013：7-8.